Инженерное проектирование и финансирование инноваций - инженерный оптимум

Введение. Одновременное рассмотрение разных аспектов реального процесса в рамках единой оптимизационной задачи всегда не хуже по итоговым результатам их последовательного, а тем более независимого рассмотрения.

В планировании технических инноваций, чему и посвящена предлагаемая статья, есть, по крайней мере, два аспекта — физический и экономический. Хочется сделать новую систему технически совершенной и финансово реализуемой. Эти естественные устремления не всегда сона-правлены и требуют совместного оптимизационного анализа.

Однако сразу решать многоаспектную задачу сложно, поэтому прибегают к поэтапному решению. Сначала проводят предварительный инженерный анализ идеи технического новшества, а в случае успеха занимаются финансовой реализуемостью, не вмешиваясь уже в физическую сторону дела. У такой последовательной схемы есть разумное оправдание. Зачем заниматься финансовой реализуемостью инновационного проекта, если он нереализуем или плох по инженерным соображениям!

Конечно, начинать надо с физики, но даже и на первом этапе исследования нельзя забывать про экономику. Выбор технических параметров проектируемой системы следует сопроводить оценками будущей прибыли от проекта, а лучше сразу сориентировать этот выбор на максимизацию прибыли, неукоснительно обеспечивая физическую допустимость системы. Иначе, без экономических оценок, трудно будет привлечь инвесторов и кредиторов, без которых невозможно реализовать сколь-либо крупный инновационный проект.

На последующем этапе более тщательного рассмотрения проблемы финансовой реализуемости проекта, когда очертится круг потенциальных инвесторов и кредиторов, целесообразно вернуться к выбору технических параметров системы, а не считать их безоговорочно фиксированными по результатам предыдущего этапа инженерного проектирования, что и будет предпринято в последующей статье.

Формулировки инженерной и финансово-инженерной задач в объемных показателях. Под инженерной, здесь понимается задача максимизации прибыли соинвесторов инновационного проекта в рамках физических ограничений, но без учета условий его финансовой реализуемости из [1], кроме сохраненного условия о достаточной относительной доходности проекта для соинвесторов. Решение такой задачи сравнивается в последующей статье с решением финансово-инженерной задачи, в которой одновременно учитываются все финансовые и физические ограничения.

Чтобы обеспечить возможность получения аналитических решений соответствующих оптимизационных задач и облегчить параметрический анализ решений, здесь совершается переход от динамического описания в потоках, изложенного в [1], к статическому описанию в объемах, менее точному, но более простому.

Задачи формируются с позиций соинвесторов, которые теперь будут распоряжаться сразу величиной интегралов x,y,z,K от прежних потоковых управлений u,v,u e ,v e из п.1 в [1]:

TT x = $ u(t)dt, У = $ v(t)dt,

TT z = PeGE J ue^dt, K = PeGE J ve^dt, 00

где x — кумулятивный объем потока первичных расходов u на проектирование и производство системы (первичные расходы управляются опосредованно — через выбор физических параметров и объема производства проектируемой системы); y — объем потока первичных доходов v от эксплуатации системы, которые могут использоваться соинвесторами на выплату дивидендов и на расплату с кредиторами; z — объем суммы потоков выплат u _e кредиторам e ∈ E , включающих возврат ранее полученного кредита и начисленных на него процентов; то есть вторичные расходы соинвесторов; K — объем суммы потоков кредитов v _e , запрашиваемых и получаемых соинвесторами, то есть вторичные доходы соинвесторов.

Ограничения на объемные управления x,y,z,K из (1) формируются интегрированием соответствующих неравенств из п. 2 в [1] и постулированием естественных свойств объемных вариантов отображений, введенных ранее в п. 1 из [1] без конкретизации этих свойств. Принадлежность ограничения к той или иной задаче помечается двузначным параметром k: к = 1 — для инженерной задачи и к = 2 — для финансово-инженерной.

Физические ограничения первичных расходов x:

a 6 x 6 b (к = 1,2),                                         (2)

где a = fix >  0 — постоянная часть затрат на проектирование и производство, независящая от физических параметров и объема производства системы; b = fix > a — верхний физически допустимый уровень затрат на проектирование и производство;

Физические ограничения первичных доходов y:

0 6 У 6 ^(x) (к = 1,2),                                       (3)

где ^(x) > 0 — известный верхний предел доходов от эксплуатации системы, монотонно возрастающий и вогнутый как функция от первичных расходов x (отсчитывается от нуля в точке а минимальных расходов из (2): ^(a) = 0).

Такой вид функции ^(x) соответствует гипотезе о рациональном расходовании средств x на проектирование и производство системы, обеспечивающем повышение ее эффективности с ростом x , но с убывающей скоростью, например

^(x) = 1 1 V x — a, где 1 1 = fix > 0 (k = 2).                         (4)

Условия достаточности кредита K для соинвесторов и его допустимости для кредиторов:

K > x — S,K > 0,K 6 m (k = 2),                          (5)

где S = fix > 0 — начальный запас собственных средств у соинвесторов, m = fix > 0 — предельные финансовые возможности всех потенциальных кредиторов (в сумме).

Практически, избыточный кредит невыгоден соинвесторам из-за увеличения последующих долговых выплат. Но теоретически, увеличение долговых выплат может парироваться быстрым дисконтирующим снижением ценности будущих денег, и тогда избыточный кредит может оказаться привлекательным для соинвесторов. Чтобы заранее не исключать такую возможность, в условиях (5) использовано ограничение кредита снизу истинными потребностями соинвесторов. При этом вместо одного нелинейного неравенства K > max{(x — S); 0} записаны два линейных: K > x — S и K > 0, эквивалентных ему в совокупности.

Договорные ограничения о выплатах z соинвесторами долгов кредиторам:

z >  ^(K )(k = 2),                                        (6)

где ф(К ) > 0,^(0) = 0 — известная монотонно возрастающая выпуклая функция от размера кредита K , взятого соинвесторами, например, линейная:

<К ) = 1 2 К,1 2 = fix > 1.                                 (7)

Предполагается, что условия договоров соинвесторов с кредиторами обеспечивают кредиторам достаточный уровень доходности кредитования проекта, поэтому надобность отдельного неравенства типа (6б) из [1] в инженерно-финансовой задаче (k = 2) отпадает.

Замечание 1. Исходное для (6) условие (3) из [1] было записано в виде ограничения снизу потока долговых выплат. Ускоренные выплаты кредита, допускаемые этим исходным потоковым неравенством, могут оказаться выгодны соинвесторам как средство экономии на процентах, если договор с кредитором это позволяет. В объемах выплат такие тонкости отследить трудно, но все равно условие (6) записано в виде неравенства. Конечно, в оптимальном для соинвесторов варианте условие (6) реализуется как равенство, но и неравенство оптимальности не помешает.

К тому же неравенство иногда удобнее, чем равенство, по техническим соображениям, когда функция ф(К ) задается по участкам с различным аналитическим представлением ^ 1 (K)^2{K ),..., таким что ф(К ) = max { ^ i (K); ^(K);... } , а функции ^ 1 ,^ 2 ,... определены всюду при K >  0. Тогда неравенство z >  ^ эквивалентно системе неравенств z > ^ i ,z >  ^ 2 ,... без указания участков активности, в то время как равенство z = ^ пришлось бы расписывать по участкам.

Итоговый баланс инвестиционного счета соинвесторов:

• (S + K + y) — (x + z) > 0    (k = 2),                            (8)

требующий неотрицательности сальдо счета в результате всех поступлений (S + K + у) и всех списаний (x + z) за все время жизни проекта.

Выполнение неравенства (8) гарантирует неотрицательности счета соинвесторов, вообще говоря, только в конечный момент времени t = T . Но если при тех же самых объемных показателях, удовлетворяющих неравенству (8), соинвесторам удастся договориться с кредиторами о своевременном выделении суммы кредитов K в пределах (5) и о распределении объема выплат z из (6), согласованном с динамикой первичных доходов y из (3), то неотрицательность счета соинвесторов будет обеспечена и во все промежуточные моменты времени.

Например, соинвесторы договариваются с кредиторами о следующем:

• 1)    кредиты в общем объеме K предоставляются импульсно в момент истощения начального запаса S собственных средств соинвесторов либо организуется кредитная линия, компенсирующая поток первичных затрат;

• 2)    все выплаты по взятым кредитам заканчиваются не позже момента времени T , но они не производятся, пока интенсивность потока первичных доходов от реализации проекта не начнет превосходить интенсивность потока первичных расходов, а скорость выплат нигде не будет превышать разности между интенсивностями этих потоков.

Замечание 2. В подтверждение достаточности такого договора проинтегрируем дифференциальное уравнение динамики текущего счета соинвесторов S (t) с одним кредитором е:

S • (t) = v(t) — u(t) + v e (t) — u e (t),     S(0) = S = fix

ТРУДЫ МФТИ. — 2011. — Том 3, № 3 Математика, управление, экономика 115 для случая ступенчатых потоков первичных расходов u(t), доходов v(t) и долговых выплат u e (t) при импульсном потоке кредитования, заданного правосторонней δ-функцией, таких что:

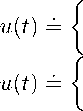
(x/t * ) при 0 6 t < t * ,

0 при t * 6 t 6 T,

0 при 0 6 t < t*, z/(T — t*) при t* 6 t 6 T,

. ( 0 при 0 6 t < t * ,

v(t) = 1                   _{+    +} / rn где t * = fix E (0,T),

( y/(T — t * ) при t * 6 t 6 T,

V e (t) = K5(t — t i ), где t i E (0,t * ) : S(t i ) = 0,

После интегрирования уравнения для S· по указанным участкам постоянства потоков при соблюдении непрерывности функции S(t) убедимся в неотрицательности решения на всех характерных временных участках, если выполняются неравенства (5), (6), и (8) для объемов x,y,z и K, а именно: m > K = x — S > 0,y > z, тогда на участке 0 6 t < ti : u(t) = (x/t*),v(t) = ue(t) = ve(t) = 0 ^

S (t) = S —

—t > 0, так как t1 = —t*; t∗                         x на участке ti 6 t < t* : u(t) = (x/t*),v(t) = ue(t) = 0,ve(t) = KS(t — t1) ^

S(t)= K — x (t t_∗

-

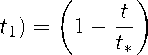
x >  0, так как K = x — S, t 1 = —t*;

x на участке t* 6 t 6 T : u(t) = ve(t) = 0, v(t) = y/(T — t*), ue(t) = z/(T — t*) ^

S(t) = ^y — z (t — t * ) > 0, так как y > z.

T - t _∗

Таким образом, в рассмотренном простом, но довольно типичном случае удается за счет необременительных соглашений с кредиторами о распределении во времени объемов кредитования и долговых выплат обеспечить достаточность «объемных» ограничений (5), (6), и (8), в общем случае лишь необходимых для поточечной неотрицательности текущего счета соинвесторов. Такой же результат достижим и в более сложных ситуациях.

Ограничение по доходности проекта для соинвесторов (подобное условие для кредиторов считается включенным в договорные ограничения (6)):

yr y + (k — 1)Кг к > [xr x + (k — 1)zr z ]I (k = 1,2),

где I = fix > 1 — уровень доходности проекта, приемлемый для соинвесторов;

r _x ,r y ,r _z ,г к = fix E (0; 1) — поправочные множители к объемам x,y,z и K , приближенно учитывающие дисконтирование соответствующих финансовых потоков u,v,u _e ,v _e из (1).

В своем исходном «потоковом» варианте ограничение по доходности проекта звучит так: отношение кумулятивного объема всех дисконтированных доходов к объему всех дисконтированных расходов должно быть не меньше желаемого уровня [2, 3].

Объемы x,y,z и K согласно их определениям (1) вычисляются интегрированием недисконти-рованных финансовых потоков, а в исходном ограничении доходности, приведенном в (6а) из [1], фигурируют дисконтированные потоки. Дисконтирующие поправки для объемов можно заранее подсчитать, если задать форму потока во времени и вычислить затем нужные интегралы.

Ниже это сделано в абстрактных обозначениях для ступенчатого и импульсного потоков, характерных для процессов инвестирования и уже использованных в замечании 2:

для ступенчатого потока с интенсивностью q —

T

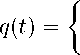
t l -t O при 0 6 t o 6 t 6 t i 6 T 0 при t < t o или t > t 1 ,

где Q =

j q(t)dt o

- недисконтированный объем,

T дисконтированный объем: J" q(t)e-Atdt o e-λt0 -e-λt1 (ti-to)A

-λt0   -λt1

поправка: r = — (t^ -^)_X — та 1 — 2 (t o + t i ) A при At i ^ 1;

для импульсного потока —

TT

q(t) =

Q5(t — t i ), j q(t)dt = Q, j

q(t)e ^{- Xt}dt = Qe ^{- Xt} 1 ,

поправка: r = e ^{- Xt} 1 та 1 — At i при At i ^ 1.

Проделав такую работу со всеми потоками, нужными для (9), и задав их форму, как в замечании 2, можно получить следующие поправки на дисконтирование для перехода к «объемному» неравенству (9) от исходного «потокового» неравенства (6а) из [1]:

• 1 — e ^-Xt*        A              e ^-Xt* — e ^-XT        A _    .

rx =   At*    ^ 1 — 2 t*^ = rz =  (T — t*)A ^ 1 — 2(T + t*), гк = e-Xt1 та 1 — Ati,t* = (S/x)ti при x > S, где все приближенные выражения получены из линейных разложений экспонент в ряд Тэйлора в окрестности нуля при AT ^ 1.

Замечание 3. Поправочные множители, используемые здесь для пересчета дисконтированных финансовых потоков в объемы, меняются при изменении формы распределения интенсивности финансовых потоков во времени. Но эти распределения должны получаться из решения динамической задачи в потоках, а не предугадываться или постулироваться, так что поправочные множители к объемам следует воспринимать как способ приближенного дисконтирования.

Однако исходная процедура дисконтирования финансовых потоков, как и всякая модель поведенческих характеристик человека, не может претендовать на высокую точность. В самом деле, «сегодняшние» деньги могут быть неудачно использованы индивидуумом, а в каком-то периоде ему остро потребуются «завтрашние» деньги для преодоления возможных кризисных обстоятельств. Если индивид хотя бы приближенно такое предвидит, то полезность завтрашних денег может им оцениваться выше, чем полезность сегодняшних.

В связи со сказанным поправочное дисконтирование объемных финансовых показателей можно представлять не как приближенное следствие дисконтирования финансовых потоков, а как исходный постулат, тоже в какой-то мере приближенный к реальности.

Чистый дисконтированный доход, максимизируемый соинвесторами:

F k = [yr y + (k — 1)Кг к ] — [xr x + (k — 1)zr z ](k = 1,2).

Этот доход здесь вычисляется тоже в объемах x,y,z и K из (1) с дисконтирующими множителями r _x ,r _y ,r _z и r K , расшифрованными после ограничения (9). Согласно экономической теории [2, 3] он представляет собой разность между суммой всех дисконтированных доходов, содержащейся в первой квадратной скобке (10), и суммой дисконтированных расходов, стоящей во второй квадратной скобке.

Итоговые формулировки оптимизационных задач для соинвесторов:

инженерная задача (k = 1) —

F _i = yr y — xr x ^ max по(х,у) € D _i ,

гдеD _i = { (x,y) : удовлетворяют условиям (2),(3) ,(9) } ;

финансово-инженерная задача (k = 2) —

F 2 = (yr y + Kr K ) — (xr x + zr z ) ^ max по (x,y,z,K ) € D 2 , где D 2 = {(x,y,z,K ) : удовлетворяют условиям (2), (3), (5), (6), (8), (9) } .

Обе задачи конечномерны и нелинейны, но доступны сравнительному аналитическому исследованию с буквенными параметрами.

Решение инженерной задачи. Решения обеих задач (11) и (12) строятся по схеме последовательной оптимизации, подробно изложенной в [4]. Сначала фиксируются все переменные, кроме одной, и аналитически находится максимум целевой функции по выделенной переменной в пределах диапазона ее допустимости для всевозможных значений остальных, фиксированных, переменных. Найденный максимум целевой функции максимизируется по очередной переменной при фиксированных оставшихся и так далее, пока состав переменных не будет исчерпан.

Если схема последовательной оптимизации дает решение, то оно и будет решением исходной задачи одновременной оптимизации. Возможные тонкости с отсутствием решений той или иной задачи, не встретившиеся ниже, проанализированы в [4].

Для облегчения восприятия все дисконтирующие множители в задачах (11) и (12) положены единичными.

Г х = Г у = r z = Г К = 1.                                   (13)

Временный отказ от дисконтирования, принятый в (13) по чисто техническим причинам не меняет характера решаемых задач.

Инженерная задача (11) остается двумерной выпуклой с одним нелинейным ограничением:

F ₁ (x,y) = У — x ^ max по(x,y) G D _i : a)a 6 x 6 b — физические ограничения расходов, б)0 6 У 6 ^(x) — физические ограничения доходов, в)у >  Ix — условие достаточной прибыльности,

где a > 0,b >  a,I > 1 — фиксированные параметры, а ^(x ) — заданная функция максимальных доходов (монотонно возрастающая, выпуклая и дифференциируемая).

Множество допустимости D i в его невырожденном варианте непусто и представляет собой криволинейный треугольник, показанный на рис. 1. Там же тонкими прямыми линиями нанесены линии уровня целевой функции F 1 (x,y) = c = fix : у = x + c и стрелочкой изображен ее градиент: V F = ( — 1;1).

Из геометрических соображений ясно, что в приведенном варианте решение задачи (14) достигается в точке касания (x * ,y * ) криволинейного участка границы у = ^(x) с самой ««высокой» из достижимых линий уровня целевой функции: у = x + c * . При более сильном ограничении x 6 b < x * решение смещается в правую угловую точку криволинейной границы.

Наличие или отсутствие решения задачи (14) определяется выполнением или невыполнением единственного условия непустоты ее множества допустимости D i . Это условие, в общем случае необходимое, здесь оказывается и достаточным для существования решения, поскольку все остальные достаточные условия из теоремы Вейерштрасса для задачи (14) всегда выполняются: множество D 1 ограничено и замкнуто, а целевая функция F 1 непрерывна.

Геометрическое отыскание решения задачи (14), произведенное на рис. 1, подтверждается далее аналитически по схеме последовательной оптимизации. При этом условие непустоты множества допустимости D1 расшифровывается тоже последовательно: сначала по одной переменной, а затем — по другой.

1°. Оптимизация доходов у при фиксированных расходах x. Фиксируется некоторое значение переменной x и по неравенствам из (14) строится соответствующее множество допустимости для переменной y:

Y^(x) = {у ^{: (x,}y) G D i при ^x = fix } = [ у^у^ )] = 0 , где y(x) = Ix,y(x) = ^(x).

Естественно, что подходят только такие значения x, для которых Y i (x) = 0 , и это требование будет присоединено, к исходным ограничениям на x из (14) при оптимизации по x.

Максимум по доходам у линейной функции прибыли F = (у — x) из (14) при фиксированных расходах x достигается на верхней границе y(x) из (15) возможных доходов:

f i (x) = maX y_GY(х) F i (x,y) = F i [x,y(x)] = maX y_G[y,y] (у — x) = у — x = ^(x) — x, где y(x) = y(x),y(x) 6 У(x),

как и можно было ожидать по экономическому смыслу.

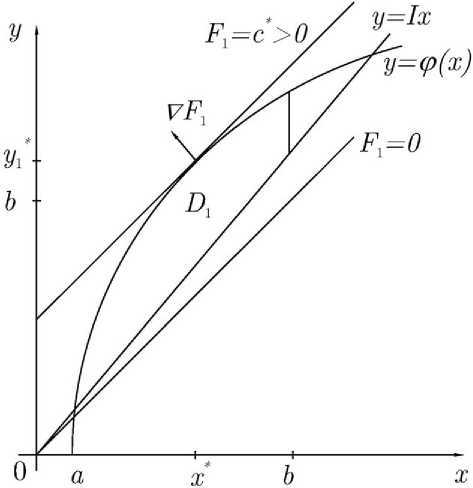
Рис. 1. Множество допустимости D 1 инженерной задачи и линии уровня F 1 = const её целевой функции

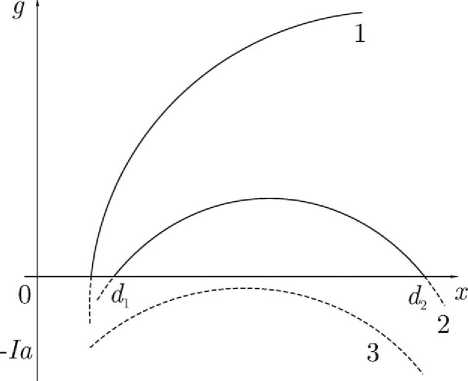
Рис. 2. Возможные варианты поведения ограничивающей функции g ( x ) = ^ ( x ) — Ix из (15) при различных значениях желаемой доходности

I :   1) I 1 = 0 , 2) 1 2 >1 1 , 3) 1 з >I 2

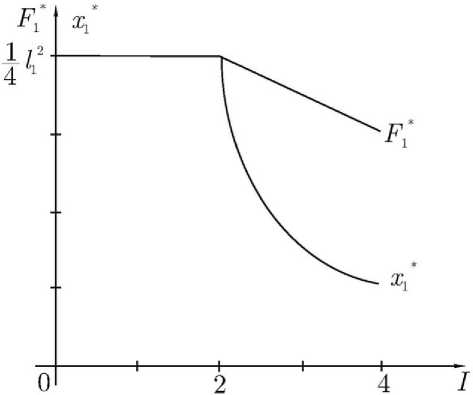
Рис. 3. Падение максимальной прибыли F ₁ ^∗ и оптимальных расходов x ^∗ ₁ при закритическом увеличении индекса I желаемой доходности

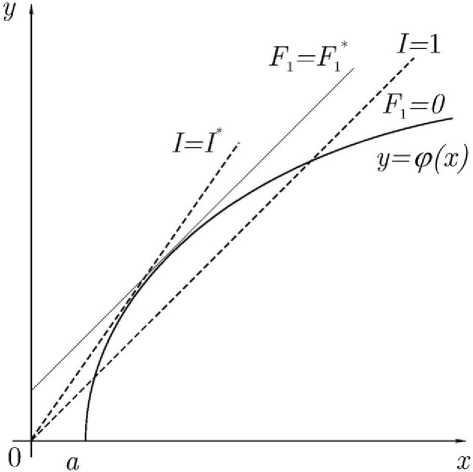
Рис. 4. Смещение светлой точки максимума индекса доходности к началу координат по сравнению с темной точкой максимума прибыли F ₁ ^∗

• 2 ° . Оптимизация расходов x при оптимальных доходах y = y(x). Строится множество X допустимых значений оставшейся переменной x, удовлетворяющих исходным неравенством из (14), наложенным непосредственно на x, а также обеспечивающих непустоту множества (15) для ранее оптимизированной переменной y:

X = { x G [a,b] : g(x) = ^(x) — Ix >  0 } = 0 .

Непустота множества допустимости X в экономических терминах означает, что хотя бы один физически реализуемый вариант проекта, индексируемый своими расходами, оказывается достаточно доходным для соинвесторов.

Чтобы аналитически построить множество (17) нужно разрешить неравенство g(x) > 0 относительно x и найти пересечение множества решений этого неравенства с отрезком [a,b].

Функция ю(x) максимально возможных доходов определена на полуоси x >  а и по предположению непрерывна, выпукла и монотонно возрастает начиная с ю(a) = 0. Поэтому уравнение g(x) = ю(x) — Ix = 0 будет иметь один d i , два d i ,d ₂ или ни одного корня по мере увеличения параметра I , что иллюстрируется на рис. 2.

Все три возможных варианта можно охватить единой записью:

d _i 6 d ₂ : g(d 1 ) = g(d 2 ) = 0,g(x) > 0 V x G (d 1 ,d ₂ ),                         (18)

если условно положить d2 = +то, когда g(x) > 0Vx > d1, и di = +то, когда g(x) < 0 Vx > a.           (19)

Для примера (4):

g(x) = l i V x - a - Ix,Vd 1,₂ - a = 2 1 ^ V (W2I ) ² - а, когда (1 _i /2I ) ² >  a, d i = + то , когда (k/2I ) ² <  a.

Пересечение отрезка [a,b] с обобщенным отрезком [di,d2] из (18), (19) дает в качестве множества допустимости (17) либо непустой отрезок [x,x], вырождающийся иногда в точку, либо пустое множество:

X = [x,x] = 0 , если b >  d i ,где x = d i > a,x = min { d ₂ ; b } ;

X = 0 , если b < d i .

Пустым множество X получается, когда желаемый уровень доходности I назначен слишком высоким, отчего всюду ^(x) < Ix, что обозначено в (19) как d i = + то , или когда по каким-то причинам максимальная физически допустимая величина расходов b оказывается слишком малой настолько, что доходы не успевают превзойти расходы в желаемое число раз I . Оба эти варианта отсутствия решения охватываются в (21) единственным неравенством b < d 1 с использованием второй условности из (19). Нижняя граница расходов x = a множеству X не принадлежит, поскольку всегда g(a) = —Ia <  0, так как ю(a) = 0.

На непустом отрезке [x,x] после максимизации по у целевая функция согласно (16) сохраняет свойства непрерывности и строгой выпуклости, постулированные для функции максимальных доходов у = ^(x). Но получившаяся функция прибыли f i (x) = ^(x) — x не обязательно будет монотонной по расходам x. Подобно ограничивающей функции g(x) = ^(x) — Ix 6 f i (x) при I >  1 функция f i (x) может остаться монотонно возрастающей, как кривая 1 на рис. 2, или может сначала возрастать, а потом убывать, как кривая 2 на рис. 2.

Максимум такой функции достигается в единственной точке x ^∗ ₁ , расположенной на правой границе x отрезка допустимости (в первом случае) или внутри этого отрезка, в точке смены возрастания функции f i (x) на ее убывание (во втором случае), что для дифференцируемых функций ю(x) может быть записано следующим образом:

max x_ex f i (x) = maX x_Gfex] V( x) — x] = f i (x ^j ) = f i ,

\ x, если^(x) > 1, _ где x = < _               , 1 x : ю (x) = 1,x = min{d2; b}.

ⁱ [ x, еслию ' (x) 6 1,

При этом согласно (16) оптимальный доход y ₁ ^∗ и максимальная прибыль F ₁ ^∗ оказываются таковыми:

У 1 = ^y(x i ⁾ = ^^(x i ^),F i = max FUx^) = ^f i ^(x i ⁾ = ^^(x i ) ^{— x} i .               ⁽²³⁾

(x,y) ∈ D 1

Полная конкретизация решения (22), (23) для иллюстративного примера (4) функции ^(x) с использованием корней d i и d 2 , найденных в (20), дает на самом широком отрезке [a,b] физически допустимых расходов с a = 0 и b > d 2 следующие результаты:

если I > 2, тою ⁰ (x) > 1 и x j = ( I ) 2 ,y j = ^{1 1} F = ^{1 2} (1 — | ) ;

0           ∗    1 2 ∗    1 2 ∗    1 2

если I 6 2,тою (x) 6 1 и x i — 4 i^,y i — 2 ii,F i — 4 1^.

В процессе последовательной оптимизации (15) — (23) найдено решение (22), (23) и установлено точное условие (21) его существования. Это же условие согласно его построению (15), (17) — (21) необходимо и достаточно для непустоты множества D 1 в исходной задаче (14) одновременной оптимизации, а значит, — и для существования решения задачи (14).

Далее, прямой проверкой можно убедиться в допустимости решения (22), (23) для задачи (14): (x i ,у * ) € D i , а любое допустимое отклонение от этого решения по его построению исходную целевую функцию не увеличивает:

V (x,y) € D1F 1 (x * ,у * ) - F i (x,y) = [F i (x * ,y * ) - F i (x,y(x))]i + [F i (x,y(x)) - F(x,y)] 2 > 0, сле-так как[...]1 = [maX x_Gx f (x)] - f (x) > 0,[...] 2 = [maX y_GY^ F i (x,y)] - F i (x,y) > 0, довательно решение (22), (23) оптимально и для исходной задачи (14).

Обратим внимание на экономическую особенность построенного оптимального решения (22), (23) инженерной задачи (14). Эта задача в дополнение к физическим ограничениям (2), (3) содержит единственное финансовое ограничение (9) о достаточной доходности проекта для соинвесто-ров. Такое ограничение уменьшает величину прибыли f i (x) в граничном варианте оптимального решения (22): x i = x = d 2 при d 2 6 b, не позволяя прибыли дорасти до величины f i (x) > f i (d 2 ), которая была бы обеспечена в точке x равенства скоростей роста доходов и расходов при отсутствии ограничения (9). На внутренний вариант максимума, представленный в нижней строке (22), это ограничение не влияет.

Негативное воздействие на максимальную прибыль F ₁ ^∗ ограничения по доходности проекта начинает проявляться с некоторого порогового значения I 1 индекса I желаемой доходности в неравенстве (9), и оно усиливается с ростом I. Это наглядно видно из решения примера, отображенного на рис. 3. Там при I < I i =2 ограничение (9) в точке x i максимума функции f (x), совпадающей со стационарной точкой x, неактивно. А затем с увеличением параметра I , стационарная точка x = 0,25l ² становится недопустимой по этому ограничению. Оптимальные расходы x ^∗ ₁ приходится уменьшать, теряя в величине прибыли из-за соответствующего падения доходов y ₁ ∗ .

Казалось бы, и целевая функция прибыли F 1 и желаемая доходность I действуют в одну сторону — в сторону увеличения доходов y. Но первое действие абсолютное, а второе-относительное. Линии уровня прибыли F i = y - x = £ = const как видно из рис. 4, идут более полого, чем линии уровня индекса доходности I = y/x = n = const > 1. По этой причине точка максимума прибыли на множестве у 6 ^(x), показанная темным кружком, располагается в зоне больших и расходов, чем точка максимума индекса доходности, показанная светлым кружком (в силу вогнутости функции ^(x) физически возможных доходов).

Конечно, должны быть веские основания, чтобы предпочесть максимум относительной доходности максимуму абсолютного объема прибыли. Например, когда есть возможность участия в нескольких проектах с высокой относительной доходностью, обещающих в сумме большой объем прибыли.

Заключение. 1. Условия финансовой реализуемости инновационных проектов, представленные в [1], после их преобразований из интенсивностей финансовых потоков в кумулятивные объемы, то есть в интегралы от интенсивностей за все время жизни проекта, становятся обозримыми и пригодными для получения аналитических решений.

Однако полученные условия объемной допустимости только необходимы, но в общем случае еще не достаточны для выполнения условий потоковой допустимости в каждый момент времени. Тем не менее в классе кусочно-постоянных и импульсных потоков пример объемно-допустимого решения удалось развернуть во времени в поточно-допустимое.

При переходе от экспоненциально дисконтированных финансовых потоков к кумулятивным объемам должны быть использованы поправочные дисконтирующие множители, вычисленные в статье для кусочно-постоянных и импульсных потоков.

Более общие условия возможности обратного перехода от финансово-допустимых объемов к допустимым потокам требуют дальнейшего анализа.

• 2.    Переход от финансовых потоков к объемам позволил сформулировать сравниваемые далее две задачи инженерной оптимизации и финансово-инженерной оптимизации в виде задач математического программирования. В инженерной задаче учитываются только физические условия

• 3.    Добавление в инженерную задачу условия по желательному уровню первичной доходности проекта, ограничивающего снизу отношение первичных доходов к первичным расходам, сужает множество допустимых первичных расходов. В результате слишком высокий уровень доходности оказывается недопустимым.

допустимости управлений и отсутствуют условия финансовой реализуемости проекта, а в финансово-инженерной учитываются все условия и предусматривается возможность финансирования проекта за счет собственных средств соинвесторов, за счет привлекаемых кредитов и доходов от реализации проекта. В инженерной задаче максимизируется первичная прибыль, а в финансовоинженерной — итоговая. Первичная прибыль — это разность между доходами от реализации проекта и расходами на проектирование и производство новшества. В итоговой прибыли из первичной вычитаются еще проценты за кредит.

Для получения аналитических решений обеих задач в рамках экономически естественных предположений оказался удобным метод последовательной оптимизации, позволивший не только строить максимизирующие стратегии для каждого управления, но и находить точные границы их существования.

Сначала уровень желаемой доходности не сказывается на инженерном оптимуме, располагающемся во внутренней стационарной точке отрезка допустимости первичных расходов, где совпадают скорости роста доходов и расходов. Рост желаемой доходности выше некоторого порогового уровня (в иллюстративном примере он оказался весьма высоким — равным двукратному превышению доходов над расходами) приводит к недопустимости стационарной точки и к падению максимального объема первичной прибыли (в примере — к линейному по индексу желательной доходности).

У разработчиков проекта должны быть веские основания, чтобы пойти на увеличение относительной доходности проекта (для привлечения соинвесторов) в ущерб абсолютному объему прибыли. Например, они должны иметь возможность предложить соинвесторам еще один проект с высокой доходностью, обещающий в совокупности с первым проектом прибыль не меньшую, чем у одного первого проекта при допороговом уровне его доходности.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 09-07-00343-а).