Исчисление трудности содержания учебно-методических средств обеспечения образования

Предлагаемый метод основывается на рассмотрении учебно-методических средств с позиций исследования структуры действий, составляющих решение мыслительной задачи. Применение графологического моделирования позволяет представить совокупность действий в виде дерева. При этом трудность действия определяется через произведение сложности действия на значение коэффициента трудности, величина которого зависит от нескольких факторов. Метод позволяет проводить комплексную оценку трудности содержания образования, обеспечивать калибровку тестов в задачах измерения качества образования (в том числе в системе ЕГЭ), сопоставлять уровни трудности отечественного и зарубежного образования.

В последние годы вновь возрастает интерес к проблеме содержания образования в связи с интеграцией России в мировое образовательное пространство, что предполагает, в частности, процедуру сопоставления ур овней качества российского и зарубежного образования. Внутри страны также имеются проблемы, связанные с необходимостью создания системы эффективного управления качеством образования. Перечисленные и другие проблемы не могут быть решены без разработки эффективных критериев трудности содержания учебно-методического обеспечения образования. Другими словами, качество образования есть его преодоленная трудность и не может быть измерено иначе, как посредством шкал трудности учебно-методического арсенала.

Распространенной характеристикой структуры решения логико-гностической задачи является ее сложность как показатель, зависящий от числа элементов структуры решения. Поскольку структуры решений задач экспертами отличаются наименьшей сложностью, возможно использование сложности таких решений в качестве объективной, а точнее, объективированной характеристики задач. В качестве другого параметра задачи мы рассматриваем трудность, которая отражает как экспертную сложность структуры решения задачи (текста, учебной задачи, структуры ответа на вопрос задания, структуры раскрытия содержания понятия, в осприятия визуального фрагмента), так и особенности обработки информации человеком, среди которых необходимо в первую очер едь учитывать две — способ поиска связей между объ ектами и ф окусирующий метод экспертных решений, в соответствии с которым решение начинается от неизвестного.

Такой подход позволяет получить эффективный инструментарий комплексной оценки трудности содержания учебно-методических средств образования, включающих в себя учебные задачи, задания, учебный текст, визуальные фрагменты. Все они могут быть рассмотрены как логико-гностические задачи, решения которых обладают соотв ет-ствующей трудностью. Суммирование же показателей трудности элементов содержания с выбранными весовыми коэффициентами позволит получить интегральную характеристику «трудность содержания образовательного кредита (учебной дисциплины и др.)».

Сущность метода

Учебно-методическое обеспечение содержания образования базируется на понятийных системах, к которым относятся логико-гностические задачи — текст, учебные задачи, в основном текстовые, вопросы, требующие реконструкции сложившегося у учащегося понятийного аппарата. К данной группе задач примыкают задачи распознавания визуальных фрагментов, предъявля-емых учащимся в составе тех или иных учебно-методических средств обеспечения образования. Такие понятийные системы, предлагаемые учащимся для осмысления, превращаются для них в проблемные ситуации со своими параметрами проблемности, среди которых в п ер вую очередь мы выделяем трудность.

Содержание образования — это уже решенные кем-то мыслительные задачи реконструкции понятийных систем: написанные учебники и учебные пособия, разработанные дидактические системы в виде сборников задач, заданий, перечней вопросов , на которые уже предполагаются верные ответы (а для некоторых тестов и неверные). Указанные решения мыслительных задач назовем экспертными в отличие от решений, предлагаемых учащимися, и будем считать их эталонными, объективированными и, если можно так выразиться, объективными. Экспертные решения являются (должны являться) наиболее простыми (краткими, рациональными).

Решение мыслительной задачи — это установление отношений между элементами структур логических конструкций, отображающих мыслительный процесс поиска результата. В качестве таких элементов могут быть выбраны де-нотаты1, текстовые субъекты и предикаты2, предикаты, входящие в основное отношение задачи3, и т. д.

Основное преимущество предикатного подхода мы видим в его универсаль- ности, по скольку пр едикаты раскрываются посредством субъектов более низкого ранга, что позволяет построить структуру решения мыслительной задачи (текста, учебной задачи, понятия и др.) в виде иер архии субъ ектов и ввести в данную структуру характеристики, отражающие особенности обработки информации человеком. Например, исследуя структуру учебного текста, можно представить связи между субъектами как операторы (модификаторы — в терминологии Л. П. Доблаева), имеющие различные параметры — коэффициенты иерархичности, коэффициенты сложности, многоэтапности модификации и др. Именно данные параметры с учетом экспертной сложности стр уктуры и обеспечивают эффективное введение такой характеристики средств учебнометодического обеспечения образования, как трудность.

В нашем исследовании мы используем фреймовую идеологию, важной особенностью котор ой является иерархичность, а в более сложных случаях — ге-терархичность представления текста, структуры решения задачи, структуры понятия, визуального фрагмента. Удобным методом изображения фрейма служит графологический, когда имена и характеристики представлены вершинами, а связи между ними — ребрами или дугами. Графологические же модели, в свою очередь, часто упрощаются до деревьев отношений, которые позволяют наглядно представить структуру решения логико-гностической задачи4.

Для решения задачи комплексной оценки трудно сти содержания образования мы применяем простое графическое (графовое) представление экспертного решения мыслительной задачи, в том числе и процесса структурирования содержания учебного текста. При этом отношения того или иного вида могут быть представлены частью дерева структуры решения соответствующей логико-гностической задачи.

Критерий трудности текстовой учебной задачи

Текстовые учебные задачи по физике, математике, химии и др. имеют от одного до нескольких действий, которые могут быть представлены в виде a = bc . Данное равенство связывает субъ екты a и c посредством опер атора b . Графическая иллюстр ация такой связи показана на рис. 1.

b ac

Р и с. 1. Пример графического представления субъект-субъектной модификации

Данное представление может быть удобным для отображения структуры учебного текста, что будет показано ниже. Для учебных текстовых задач более удобно другое представление (рис. 2):                a

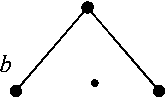
Р и с. 2. Представление действия a = bc в виде элементарного дерева

Базовой характеристикой структуры решения учебной задачи является ее экспертная сложность. Трудн о сть же мы связываем с особенностями интеллектуального поиска. Таким образом, критерий трудности учебной задачи включает в себя как критерий сложности структуры решения задачи, так и критерий стратегии, обеспечивающей самое эффективное решение задачи. В случае наиболее распространенных и эффективных фокусирующих стратегий, когда решение начинается от неизвестного, мы суммируем показатели сложности отдельных действий с учетом их трудности. Трудно сть того или иного действия в самом простом случае определяется как произведение сложности действия (масштабированной сложности) на значение коэффициента трудности, величина которого равна единице для последнего действия в реше- нии задачи и возрастает на единицу при переходе к предыдущему действию.

Для иллюстрации метода рассмот- рим следующую задачу.

Проводка от магистрали в здание осуществляется проводом, сопротивление которого Rпр. Напряжение магистрали постоянно и равно U. Какова может быть максимальная потребляемая в здании мощность Р, если напряжение на включенных в цепь приборах не должно падать ниже U0 ?

По рис. 3 видно, что задача имеет три действия, коэффициенты трудно сти которых согласно вышеупомянутому ме- тоду их исчисления принимают значения 1, 2 и 3. Назначим каждому из этих действий определенную сложность, например С = 20. Тогда для первого действия трудность буд ет равна 60 (3 · 20), для второго — 40 (2 · 20), для третьего — 20. Суммарная трудн ость задачи, таким образом, равна 120.

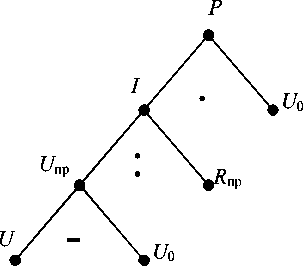
Р и с. 3. Граф структуры экспертного решения задачи

k = 3

k = 2

k = 1

Трудность понятия

Для исследования структуры понятий мы также используем фреймовые представления. То или иное понятие, как и фрейм, имеет имя. Понятия, через которые непосредственно раскрывается содержание исходного термина (имени), могут быть названы базовыми характе- ристиками. Все вместе они образуют иерархическую структуру — систему ярусов. Ближайший к имени понятия ярус представляет собой совокупность непосредственно раскрывающих смысл исходного термина понятий. Следующий ярус понятий раскрывает смысл понятий предыдущего яруса и т. д. Для определения трудности понятия в самом простом варианте метода суммируются трудности процедур установления связей вышележащих понятий с нижележащими с учетом условно выбираемой величины сложности элементарной структуры, каковой являются понятия и связь между ними.

На рис. 4 показаны два ранга подобных структур. Первый, высший, ранг составляют структуры Aa , Ab , Ac . Второй, более низкий, ранг включает структуры ad , ae , bf , cg , ch , ck . Назначим для примера величину сложности каждой из упомянутых стр уктур, р авную единице. Для того чтобы пер ейти к расчету трудно сти понятия, необходимо ввести параметры трудности, зависящие от особенностей обработки информации человеком. В простейшем случае выбирается один параметр, который может быть назван коэффициентом иерархичности и введен следующим образом. Поскольку определяющими дальнейшее раскрытие понятия являются структуры высшего ранга, то им присваивается значение коэффициента иерархичности на единицу выше, чем структур ам нижележащего уровня. В нашем примере, как мы видели, имеется всего два ранга связей. Поэтому структурам Aa , Ab и Ac можно присвоить значение коэффициента иерархичности, равное 2, а структурам более низкого ранга — 1.

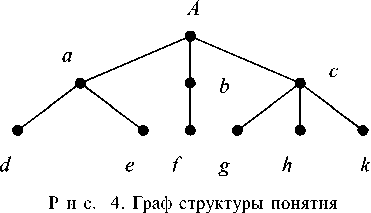
С учетом сказанного трудность понятия, структура которого показана на рис. 4, вычисляется следующим образом . Поскольку структур высшего ранга всего три, а коэффициент иерархичности для каждой из них равен 2, то суммарная трудно сть структур высшего ранга равна 6. Структур же низшего ранга всего шесть при коэффициенте иерархичности, равном 1. Поэтому трудность связей низшего ранга также равна 6. Отсюда результирующая трудн ость понятия, структура которого показана на рис. 4, равна 12.

Для того чтобы увеличить разрешение системы исчисления трудн ости понятий, достаточно установить требуемое значение сложности элементарной структуры.

Структура и трудность содержания учебного текста

Текст, как и само знание, выражением котор ого он является, может иметь весьма сложное строение. Одно и то же предложение бывает одновременно текстовым субъектом и текстовым предикатом (частью предиката). Предикат определенного ранга н ер едко включает в себя один, два и более отдельных параллельных субъектов, либо субъект и его предикат (несколько субъектов и предикатов) более низкого ранга; последний, в свою очередь, может содержать субъекты и пр едикаты еще более низкого ранга, и т. д.

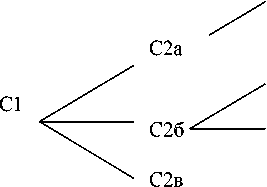
Из схемы, показанной на рис. 5, видно, что текстовый субъект может модифицироваться в одном субъекте последующего ранга (целостная модификация) или в нескольких (раздельная модификация). Некоторые текстовые субъекты не имеют модификаций и являются конечными. Другие имеют только непосредственную модификацию: их модификата-ми являются субъекты одного последующего ранга, которые далее не модифицируются (конечные). Наконец, третьи получают кроме непосредственной также и опосредованную модификацию —

через свои более близкие модификаты. Например, начальный субъект, выраженный заглавием, непосредственно модифи- цируется в субъектах второго ранга и опосредованно — в субъектах третьего, четвертого и последующих рангов.

С3

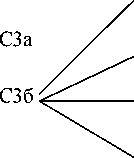
С4а                        С6а

С4б         С5            С6б

С4в         С5

С4г         С5а

С5б

С5в

Р и с. 5. Структура текста по Л. П. Доблаеву5

Таким образом, система субъектов текста оказывается системой модификации выраженного в заголовке начального субъ екта. Сравнивая различные способы модификации текстовых субъектов, нетрудно увидеть, что более простыми из них для понимания, но в то же время и менее информативными являются уточнение и, особенно, повторение и расчленение того, что выражено в модифицируемом субъ екте; наиболее сложными и вместе с тем информативными — выявление новых предметов мысли или их признаков.

Наиболее просто расчет трудности текста может быть проведен следующим образом. На основании структурной схемы выделяются линии модификации, для каждой из которых определяется трудность как сумма произведений сложности (условной, масштабированной) перехода между соседними субъ ек-тами на ряд коэффициентов, зависящих от места модификации в ее последовательности и типа модификации. Затем суммируются показатели трудн ости для всех линий модификации, входящих в задачу определения трудности соответствующего фрагмента, например абзаца либо параграфа учебника. Однако при этом теряется важная информация о трудности содержания узлов структур -ной сети, в качестве которых фигуриру- ют текстовые субъекты, денотаты и др. Иерархическая структура субъ екта, денотата, понятия, фрейма позволяет все же рассчитать трудно сть структуры по методике, котор ая предложена нами выше в разделе, посвященном трудно сти понятия. Другими словами, учет трудности субъ екта, денотата, предикатемы и пр. позволяет более точно определить такой показатель учебного текста, как его трудность.

Ниже на простом примере (рис. 6) рассмотрим расчет трудности текста как без учета трудности субъектов, входящих в отрезок линии модификации, так и с ее учетом.

С 1

С 2

С 3

Р и с. 6. Часть линии модификации

Пусть имеется линия модификации, включающая три субъекта: С1, С2 и С3. Не зная параметров сложности структур субъектов, мы вынуждены назначить эту сложность произвольно, например равной

Параметрами трудн о сти в рассматриваемом примере являются коэффициенты иерархичности, значения которых равны 2 для первого действия и 1 для второго ( k_{i 1} = 2, k_{i 2} = 1). Подобный подход мы использовали при рассмотрении как трудно сти текстовой задачи (см. рис. 3), так и стр уктуры понятия (см. рис. 4). В качестве другого параметра трудности можно ввести, например, величину коэффициента модификации, зависящую от вида отношения между субъектами. Для уточнения и повтор ения эта величина может быть положена равной 1, для выявления же новых пр едм етов мысли и их признаков — 2. Допустим, в нашем примере k_{m 1} = 2, k_{m 2} = 1. Разумеется, могут быть использованы и другие классификации отношений и соответствующих коэффициентов модификации, в том числе концепция шагов догадки Н. И. Жинкина и метод постановки вопросов Л. П. Доблаева. С учетом выбранных значений результирующая трудность рассматриваемой линии модификации равна

10 k i 1 k m 1 +10 k i 2 k m 2 = 50.

Стр огий учет параметров трудно сти текстовых субъектов, денотатов, фреймов и др., пример которого показан выше в разделе, посвященном рассмотрению стр уктуры понятия, позволяет получить более точные р езультаты, а единый подход к исчислению трудности учебно-методических средств обеспечения образования — эффективный способ комплексной оценки трудности содержания образования.

Визуальные фр еймы отражают алгоритмы работы зрительной системы, и трудность организации фрейма может

ОБРАЗОВАНИЯ шшшшшшш быть рассчитана так же, как и трудно сть формирования структуры решения логико-гностической задачи другого типа: учебной задачи, понятия, текста. Например , в работе М. Минского⁶ рассмотрен подробный пример представления изображения куба в виде графа, что дает нам возможность применить графологический анализ к исчислению трудности восприятия геометрической фигуры.

Таким образом, предлагаемая методология и основанный на ней инструментарий позволяют эффективно проводить комплексную оценку трудности содержания образования, а также ввести количественный критерий расхождения требований школьного и вузовского образования по основным учебным дисциплинам. Кроме того, данный метод может быть применен для точной калибровки тестов в задачах измерения качества образования (в том числе в системе ЕГЭ), для сопоставления уровней трудности отечеств енного и зарубежного образования и других целей.