Использование алгоритма имитации отжига для обучения сети ТСК

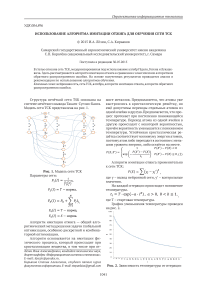
Структура нечёткой сети TSK основана на системе нечёткого вывода Такаги-Сугэно-Канга. Модель сети ТСК представлена на рис. 1.

Рис. 1. Модель сети ТСК

Параметры сети:

,

F₂(0 = T — норма,

N

,

Р₄(.П = T — норма, F₅(/) — S — норма.

Алгоритм имитации отжига — общий алгоритмический метод решения задачи глобальной оптимизации, особенно дискретной и комбинаторной оптимизации.

жиге металлов. Предполагается, что атомы уже выстроились в кристаллическую решётку, но ещё допустимы переходы отдельных атомов из одной ячейки в другую. Предполагается, что процесс протекает при постепенно понижающейся температуре. Переход атома из одной ячейки в другую происходит с некоторой вероятностью, причём вероятность уменьшается с понижением температуры. Устойчивая кристаллическая решётка соответствует минимуму энергии атомов, поэтому атом либо переходит в состояние с меньшим уровнем энергии, либо остаётся на месте.

'        1           FOO - F(X) < 0

Р(Х,Г)=1    ( F(X')-F(X)\

Алгоритм имитации отжига применительно к сети ТСК:

, где y – выход нейронной сети, y’ – контрольные значения.

На каждой итерации происходит понижение температуры.

ti = T • exp(—a • ib), a > 0, 0 < b < 1, где T – стартовая температура.

График уменьшения температуры приведен на рис. 2.

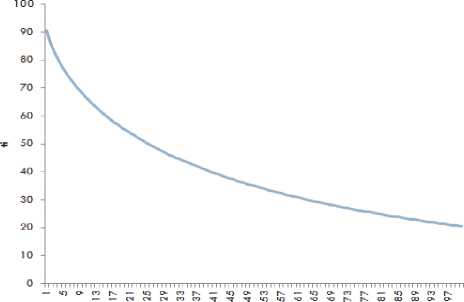
Рис. 2. Зависимость температуры от итерации

Известия Самарского научного центра Российской академии наук, т.17, №2(5), 2015

Новые коэффициенты X’ рассчитываются по формуле:

Xj' = sgn ^a-^-Xj-k- , где a – равномерно распределённая на отрезке [0, 1] случайная величина.

График зависимости отклонения параметров от итерации приведен на рис. 3.

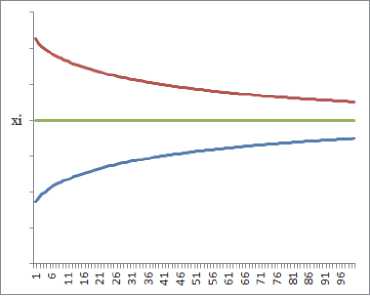
Рис. 3. Зависимость отклонения параметров от итерации

Сравнительный анализ алгоритмов обратного распространения ошибки и алгоритма имитации отжига осуществлялся на выборке из 160 объектов. Число входных параметров N – 3. Число правил M – 5. Число классов K – 3.

Рассмотрим далее различные варианты построения сети ТСК в зависимости от выбранных операций T-нормы и S-нормы. На рисунках будут приведены зависимости числа ошибок от итерации обучения для двух указанных алгоритмов при решении задачи идентификации. В качестве исходных данных взята классическая задача ирисов Фишера.

ТСК сеть на основе операций сложение и произведение.

.

.

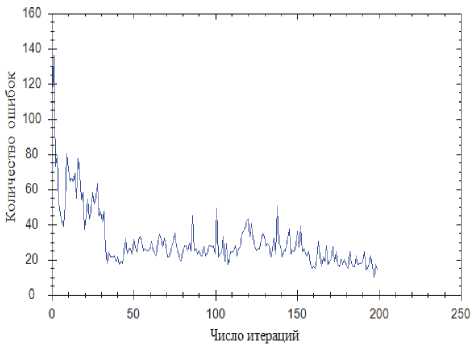
Рис. 4. Алгоритм имитации отжига

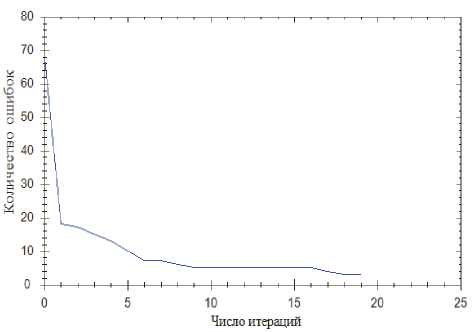
Рис. 5. Алгоритм обратного распространения ошибки

ТСК сеть на основе алгебры Гёделя.

.

.

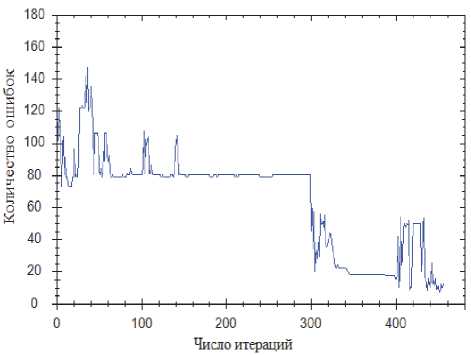
Рис. 6. Алгоритм имитации отжига

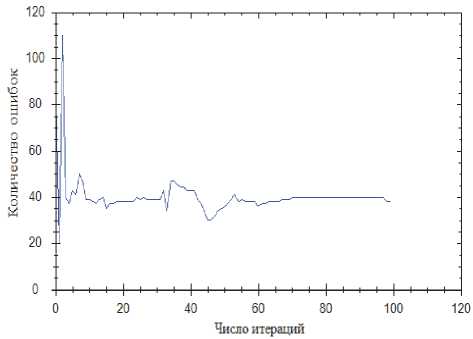
Рис. 7. Алгоритм обратного распространения ошибки

ТСК сеть на основе алгебры Гогена.

.

.

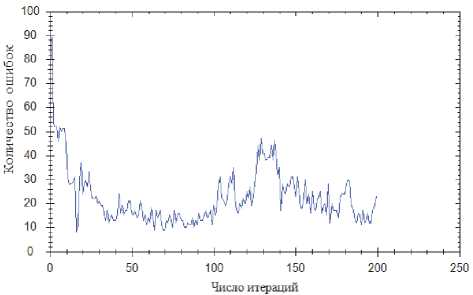
Рис. 8. Алгоритм имитации отжига

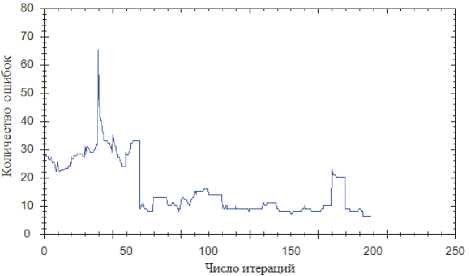
Рис. 11. Алгоритм обратного распространения ошибки

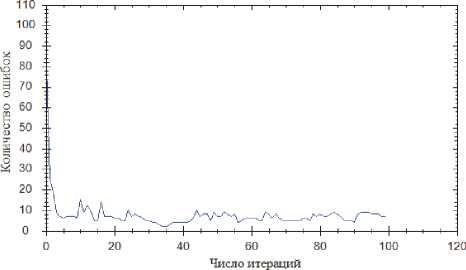
Рис. 9. Алгоритм обратного распространения ошибки

торые можно дифференцировать, алгоритм обратного распространения ошибки показывает лучший результат за меньшее число итераций. В алгебрах, где указанные операции не дифференцируемы и их дифференциал заменялся некоторой суррогатной функцией, алгоритм имитации отжига показывает меньшее число ошибок, но при этом требует большего числа итераций обучения.

В случае с алгеброй Лукашевича из-за ограничений функции сверху и снизу невозможно оценить новое состояние, поэтому алгоритм имитации отжига работает некорректно.

ТСК сеть на основе алгебры Лукашевича.

Sn(X) = Min(l,^ x₍) .

Tn(X) = Max(O,Max(X) + Max(X’) - 1,).

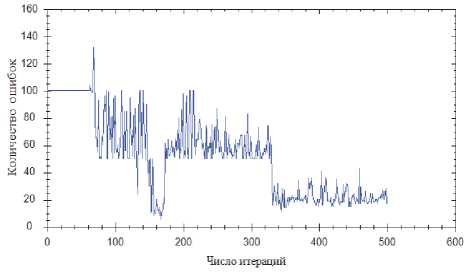
Рис. 10. Алгоритм имитации отжига

Как видно из результатов испытаний, в алгебрах, где используются операции S-нормы и T-нормы, ко-