Использование анализа соответствий и лог-линейных моделей для исследования факторов, влияющих на сердечно-сосудистые заболевания

Сердечно-сосудистые заболевания являются основной причиной смерти во всем мире, унося ежегодно около 17,9 млн жизней как в развитых странах, так и в странах третьего мира.

В частности, в России ишемическая болезнь сердца является подклассом сердечно-сосудистых заболеваний и одной из основных причин смерти людей.

Среди общего показателя смертности в мире от всех болезней 20 % мужчин и 12 % женщин умирают от сердечно-сосудистых синдромов [29]. Статистические исследования показывают, что около 3 млн человек страдают сердечными заболеваниями и 2 млн страдают стенокардией, которая является наиболее типичным симптомом ишемической болезни сердца. Обычно от этого недуга больше страдают мужчины, чем женщины. Однако вероятность развития симптомов сердечно -сосудистых заболеваний в пожилом возрасте у мужчин и женщин одинакова [13].

Сердечно-сосудистые заболевания становятся одной из основных причин смерти в развивающихся странах, таких как Индия, Шри-Ланка, Пакистан и многих других, включая Россию. Ишемическая болезнь сердца вместе с сердечным инсультом - самые серьезные убийцы в мире, уносящие более 17 млн жизней ежегодно. В частности, в Пакистане 30-40 % всех смертей вызваны ишемической болезнью сердца, что составляет почти 200 000 человек в год. Ишемическая болезнь сердца в настоящее время является основной причиной смерти в Пакистане. Согласно последним данным Всемирной организации здравоохранения, опубликованным в апреле 2018 , смертность от ишемической болезни сердца в Пакистане достигла 1 403 000 человек, или 29 % от общего числа смертей, и стала основной причиной человеческих смертей в Пакистане. Многие исследования показали, что более 60 % смертей были вызваны сердечными заболеваниями в развивающихся странах. Прогнозируется, что к 2030 году 23 млн человек могут ежегодно умирать от сердечно-сосудистых заболеваний [7].

Развивающиеся страны также сталкиваются с усилением ишемической болезни сердца / сердечно -сосудистых заболеваний из-за неправильного питания. Поэтому необходимо информировать людей о сердечных заболеваниях, чтобы снизить риски в этих странах. Женщины считаются потенциальными жертвами сердечно-сосудистых заболеваний в Пакистане, и ишемическая болезнь сердца поражает не только стареющий женский пол, как считалось ранее, но и женщин в возрасте от 30 до 40 лет [17; 18].

Математический анализ корреляции между сердечно-сосудистыми заболеваниями и различными факторами

Недавно были опубликованы статьи, посвященные поиску математической корреляции между сердечнососудистыми заболеваниями и различными факторами.

Li et al . [20] использовали категориальный анализ параметров [1] для изучения больших данных (включая артериальное давление, липиды крови, уровень глюкозы в крови, физическую активность, курение табака, употребление алкоголя, избыточный вес или ожирение, а также частоту потребления фруктов, овощей, зерна, бобовых и красного мяса) в рамках общенационального проекта скрининга населения, охватившего 152 сельских округа и 100 городских округов из 31 провинции Китая. Авторы обнаружили, что высокий риск сердечно -сосудистых заболеваний проявляется в регионах Северного Китая, жители которых сталкиваются с общими проблемами со здоровьем, такими как ожирение и высокое давление, а также потребление нездоровой неосновной пищи (низкое потребление фруктов и овощей или высокое потребление красного мяса). Жители Южного Китая с более низким риском сердечно -сосудистых заболеваний, чем на Севере, имели наибольшее распространение нездоровой основной пищи (низкое потребление зерновых и бобовых), аномальный метаболизм (глюкоза и липиды) и низкую физическую активность.

Аналогичное исследование, проведенное в восточной части Китая с использованием анализа лог -регрессии [26], показало, что около 30 показателей связаны с сердечно-сосудистыми заболеваниями, включая пол, возраст, семейный доход, курение, употребление алкоголя, ожирение, аномальный уровень холестерина, аномальный липопротеин низкой плотности, аномальный уровень глюкозы в крови натощак и т.д. Для построения модели прогнозирования этого заболевания использовались несколько математических методов, включая модель многомерной регрессии, алгоритм CART ( Classification and Regression Trees ), Байесовские сети, бэггинг, метод случайного леса ( random forest ) и т. д. Среди них модель многовариантной регрессии использовалась в качестве тестовой модели для оценки производительности [4]. Результаты показали, что метод случайного леса превосходит другие методы и дает значительно лучшие результаты по сравнению с тестовой моделью. Более того, в модели прогнозирования сердечно -сосудистых заболеваний для трехлетней оценки риска вес переменной «возраст» достаточно велик, что не позволяет модели выделить долгосрочный риск в более молодых возрастных группах.

Курение также можно рассматривать как один из основных факторов, влияющих на тяжесть сердечно -сосудистых заболеваний. Рандомизированные исследования подтверждают преимущества реабилитации на основе физических упражнений в отношении факторов риска сердечно-сосудистых заболеваний. Связь между кардиологической реабилитацией на основе физических упражнений и снижением факторов риска сердечно-сосудистых заболеваний у пациентов из Швеции через год после инфаркта миокарда была изучена Sjölin et al. [22]. Было показано, что люди, которые очень активны, чаще сообщали о том, что бросают курить, и те, кто физически активны, достигли несколько большего снижения уровня триглицеридов за один год, по сравнению с теми, кто не занимался упражнениями. Участники-мужчины набрали меньше веса, в то время как участники-женщины достигли лучшего контроля липидов по сравнению с не-участниками.

Basu et al. [2] представили модель для количественного прогнозирования дифференциального воздействия различных мер борьбы против табака и фармакологической терапии на инфаркт миокарда и смертность от инсульта, стратифицированную по возрасту, полу и городскому / сельскому статусу с 2013 по 2022. Репрезентативны данные из Индии о множественных факторах риска, влияющих на инфаркт миокарда и смертность от инсульта, включая гипертонию, гиперлипидемию, диабет, ишемическую болезнь сердца и цереброваскулярные заболевания. Также были включены данные из Индии о курении сигарет, жевании табака и пассивном курении. Согласно результатам модели, ужесточение законодательства об ограничении курения и повышение налогообложения табака, вероятно, будут наиболее эффективной стратегией борьбы против курения (включая также краткие рекомендации по прекращению курения со стороны медицинских работников, кампании в средствах массовой информации и запрет рекламы) для снижения смертности от инфаркта миокарда и инсульта в течение следующего десятилетия. Предполагается, что введение ограничений в виде рекомендаций по прекращению употребления табака будет наименее эффективной стратегией на уровне населения. В сочетании друг с другом эти меры по борьбе против использования табака могут предотвратить 25 % инфарктов миокарда и инсультов, если эффекты вмешательств будут дополнять друг друга. Несмотря на рост числа факторов риска сопутствующих сердечно -сосудистых заболеваний, таких как гиперлипидемия и гипертония, в странах с низким и средним уровнем дохода, борьба против табака, вероятно, останется высокоэффективной стратегией снижения смертности от сердечно -сосудистых заболеваний.

Основная цель данной статьи - определить влияние образа жизни (например, качество продуктов питания, курение и т.д.) и пищевых привычек городских жителей Пакистана на риск ишемической болезни сердца с помощью статистического анализа набора данных, собранных у кардиологических пациентов в городе Фейсалабад (Пакистан). Для этого мы предла- гаем два статистических подхода: «анализ соответствия» и «логарифмическая линейная модель» - для проведения исследования, преследующего следующие цели:

• 1)    изучение фактора риска ишемической болезни сердца;

• 2)    количественная оценка наиболее вероятных факторов риска, связанных с ишемической болезнью сердца, с использованием множественных корреляционных и лог-линейных моделей;

• 3)    оценка степени зависимости от различных факторов сердечного риска ишемической болезни сердца.

Методология

Комбинированный анализ категориальных данных (с использованием анализа множественных соответствий и лог-линейной модели) был использован для оценки данных обследования кардиологических пациентов в Институте кардиологии Фейсалабада (Фейсалабад, Пакистан) [15]. В выборке участвовали люди, страдающие сердечнососудистыми заболеваниями и/или проблемами, связанными с сердечно-сосудистыми заболеваниями, чтобы можно было легко судить об их привычках и сделать результаты более точными. Выборка была отобрана с учетом погрешности (доверительный интервал) на уровне ± 3 %, уровень достоверности 95 %, вариабельность (стандартное отклонение) составила 0,5.

Таким образом, размер выборки был определен по приведенной ниже формуле (1) согласно [5]:

N = Z ² о ¹ —⁰ ,                  (1)

e где N - размер выборки; значение Z составляет 1,96; о составляет 0,5, а e = 0,03 - погрешность.

Значение Z взято из таблицы z -распределения. Для качественных исследований требуется минимальный размер выборки не менее 12 для достижения насыщения данными [6; 9; 12]. Используя уравнение (1), мы получили N = 1067. Данный размер выборки был сочтен достаточным для качественного анализа и масштаба этого исследования.

Для опроса участников исследования была составлена анкета из 31 различного вопроса, выявляющих факторы, потенциально влияющие на развитие ишемической болезни сердца (возраст, пол, уровень образования, вес, рост, процедура реваскуляризации, анамнез сердечных заболеваний, анамнез диабета, курение, режимы физических упражнений, условия проживания, бессонница, аппетит, стресс и депрессия, питание). Затем данный опрос прошли отобранные респонденты, которые были исследованы на предмет их образа жизни в области питания и медицин ских факторов риска, включая развитие коронарных синдромов. Респонденты были выбраны в разных возрастных и гендерных группах

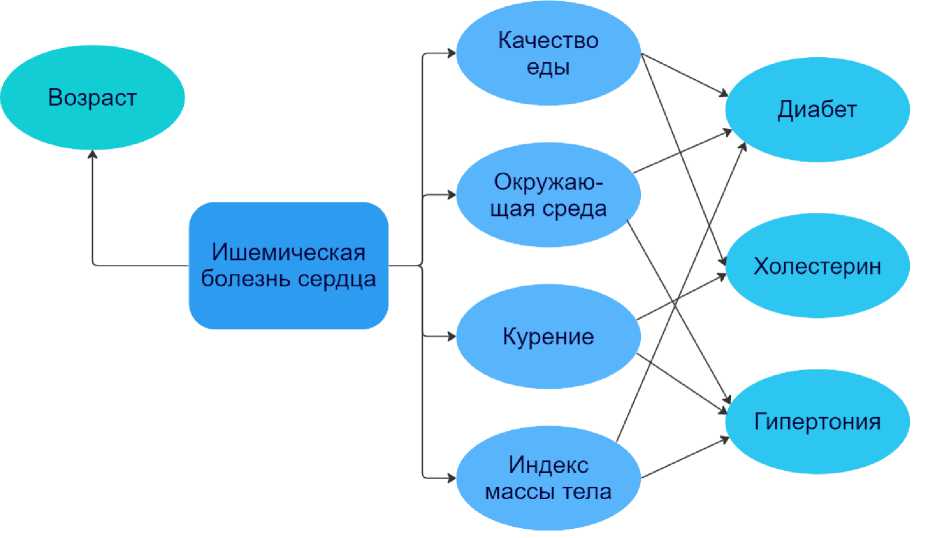
Рис. 1. Модель корреляции факторов

Лог-линейный анализ - это независимая процедура для учета распределения наблюдений в перекрестной таблице категориальных переменных. Это разновидность многофакторного частотного анализа [8]. В некоторой литературе лог-линейный анализ был назван многофакторным частотным анализом. Согласно [11], этот метод используется для измерения силы ассоциации между набором переменных без концептуального различия между переменной ответа и набором объясняющих переменных.

Анализ множественных соответствий стал популярным из-за его гибкости при сопоставлении с любыми категориальными или некатегориальными данными [14; 16]. Что касается категориальных данных, предполагается, что нет распределения и гипотетической модели при условии декомпозиции структуры данных. Многие исследователи пытались объединить многомерные и категориальные методы и найти различия между анализом соответствий и модельным подходом. Они пришли к выводу, что при определенных условиях комбинированные методы (многомерные и категориальные) мало чем отличаются [11].

Нулевую гипотезу статистической значимости можно записать как:

H ₀ : X AB = 0, для всех значений i и j .       (2)

Подход в данной статье заключается в том, чтобы, во-первых, применить анализ множественных соответствий для выбора условий с высоким уровнем взаимодействия, чтобы уменьшить количество взаимодействий. Во-вторых, к параметрам с высоким уровнем взаимодействия применяется лог-линейная модель. Данная процедура позволяет упростить вычислительный процесс за счет сокращения количества переменных.

На рис. 1 представлена концептуальная схема процесса классификации и корреляции факторов для ишемической болезни сердца. Можно заметить, что эти параметры взаимосвязаны друг с другом и зависят друг от друга.

Анализ множественных соответствий сыграл роль процесса отбора, чтобы сделать окончательную модель более простой и точной [1].

Три группы факторов включают:

• 1)    неизменяемый биологический фактор риска (возраст, семейный анамнез, диабет);

• 2)    факторы риска, адаптируемые к лечению (гипертония и холестерин);

• 3)    факторы риска, поддающиеся изменению образа жизни (курение, режимы и качество питания, среда проживания и сидячий образ жизни).

Как правило, в качестве руководства для этого процесса могут использоваться либо теоретические, либо эмпирические данные. Если априорной гипотезы не существует, можно использовать два подхода:

• •    начинать с «полной» модели, то есть модели, имеющей «достаточное количество» данных (наблюдений), а затем удалять интерактивные члены более высокого порядка, пока не будет достигнуто соответствие данных. Этот процесс должен быть основан на вероятностных стандартах, предложенных исследователем;

• •    начинать с простой модели и затем добавлять более сложные интерактивные члены, пока не будет получено приемлемое соответствие данных. Также необходимо гарантировать, что дополнительные условия не будут существенно изменять концепцию, гипотезу или процесс создания окончательной модели.

Следующее уравнение представляет многомерную таблицу сопряженности 2 х 2 с тремя переменными (каждая с двумя уровнями, см. табл. 2 (Приложение)), используется для демонстрации иерархического подхода:

Ln ( F j ) = Ц + ^Х A ^{+ Х} B ^+Х к ^+Х AB ^{+ Х} AC ^{+ Х} BC ^+Х AB • (3)

Иерархия моделей может существовать всякий раз, когда сложная многомерная связь, присутствующая в данных, требует учета менее сложных взаимосвязей. Например, в приведенном выше уравнении (3), согласно [8], при наличии трехстороннего взаимодействия ( ABC) уравнение для модели также должно включать все двусторонние эффекты ( AB , AC , BC) , а также переменные ( A , B , C) и среднее значение (μ). Другими словами, менее сложные модели вложены в модель взаимодействия более высокого порядка ( ABC) , то есть более сложную модель. Следует отметить, что такой способ обозначения (буквы в скобках) используется для описания сценариев модели, что означает, что каждый набор букв в скобках указывает параметр эффекта высшего порядка, включенный в модель, и иерархию. Набор букв в скобках также показывает, что обязательно присутствуют связи более низкого порядка [19].

Для наибольшей эффективности процедура подгонки должна обеспечивать (i) хорошие параметры; (ii) оценку ошибок по этим параметрам и (iii) статистическую меру согласия (критерий согласия). Критерий хи-квадрат определяется следующим образом: если каждая точка данных ( x_a , ya ) имеет собственное известное стандартное отклонение g _а так, что оценка максимального правдоподобия параметров модели получается путем минимизации приведенной ниже величины:

У - - y ( x ; a - ••• a m )

N х2 = 3

с -

Это критерий хи-квадрат для моделей, линейных относительно а . Однако оказывается, что распределение вероятностей для различных значений х² при его минимуме может быть получено аналитически и, следовательно, является распределением хи-квадрат для ( N-m ) степеней свободы.

Практическое правило состоит в том, что «типичное» значение х2 для «умеренно» хорошего соответствия со ставляет х2 ~ v. Точнее, это утверждение, что статистика х2 имеет среднее значение v и стандартное отклонение 2vv, и асимптотически при больших v становится нормально распределенным. В некоторых случаях неопределенности, связанные с набором измерений, заранее неизвестны, и соображения, связанные с подгонкой х2, используются для получения значения для σ [3]. Если предположить, что все измерения имеют одинаковое стандартное отклонение, gi = g, то можно сначала присвоить произвольную константу g всем точкам, затем, подгоняя параметры модели, минимизируя х2 и, наконец, пересчитав g:

3 ( У а — У ( X-))2 G2 = —--------- N — m

Очевидно, такой подход исключает независимую оценку степени соответствия; факт, который иногда упускают из виду его приверженцы. Однако, когда ошибка измерения неизвестна, этот подход позволяет назначать точкам границы погрешностей. Если взять производную уравнения (4) по параметрам ak, получим уравнение для погрешности при минимуме х2.

у Г ^ya ^{— У (} x i ) Y C y ⁽ x ij ••• a k •••) ^ а = 1 1    ст ²      J(       В a k      J

Были использованы методы обработки данных, и поэтому количество данных было сокращено перед проведением логарифмического линейного моделирования, таким образом, разница в степенях свободы оправданна [24].

В данном разделе представлена наилучшая выбранная иерархическая модель. Выбранная модель должна учитывать все важные взаимодействия между переменными. После применения анализа множественных соответствий был выполнен лог-линейный анализ для получения наилучших результатов. В модель включены слагаемые, отвечающие за влияние как отдельных факторов, так и их многосторонних взаимодействий:

ln ( m gascodh ) = Ц + Х g + Х a + Х s +Х c +Х ^о +

+Х d + Х h + Х scod + Х gsd + Хgdh + Хsdh + Х cdh,        (7)

где верхние индексы обозначают: g = пол, a = возраст, s = курение, c = уровень холестерина, о = ожирение, d = гипертония, h = инфаркт миокарда; и их комбинации можно понимать как: scod = курение + уровень холестерина + ожирение + гипертония; индекс gascodh означает комбинацию всех факторов.

Перед выполнением нашего анализа в соответствии с ранее описанной методологией мы должны проверить надежность анкеты с помощью метода альфы Кронбаха, который предлагается в качестве оценки надежности [22].

В этом методе, предложенном Ли Кронбахом, сравнивается разброс каждого элемента с общим разбросом всей шкалы. Если разброс результатов теста / анкеты меньше, чем разброс результатов для каждого отдельного вопроса, следовательно, каждый отдельный вопрос направлен на исследование одного и того же общего основания. Они вырабатывают значение, которое можно считать истинным. Если такое значение выработать нельзя, то есть получается случайный разброс при ответе на вопросы, тест не надежен и коэффициент альфа Кронбаха будет равен «0». Если же все вопросы измеряют один и тот же признак, то тест надежен и коэффициент альфа Кронбаха в этом случае будет равен «1».

Данный метод необходимо использовать для формирования масштабируемых параметров и проверки их согласованности и надежности. На практике считается, если значение альфы Кронбаха составляет от 0,6 до 0,9, то данные опроса или теста считаются отличными [16].

Процесс проверки проводился по двум измерениям (см. табл. 2 и 3 (Приложение)), где альфа Кронбаха составляла от 0,6 до 0,8, следовательно, данные надежны. Затем был проведен анализ соответствий на первом этапе без каких-либо изменений в данных. Столбцы, содержащие только нулевые значения или «Неприменимо» ( N / A ),

N

2*

-2-

-4"

-6-

-8'

о6 203

о7 198

Статистика: Столбец координат и вклад в инерцию

Соотв: таблица ввода (строки и столбцы)

Анализ: Общая инерция = 1

-12                 -9

Измерение 1

■6

-3

271      231

73 ^67® 127

® °28®2

59   о;.

133 173

°648 174

1^5

46 14

о

Основная нормализация переменной

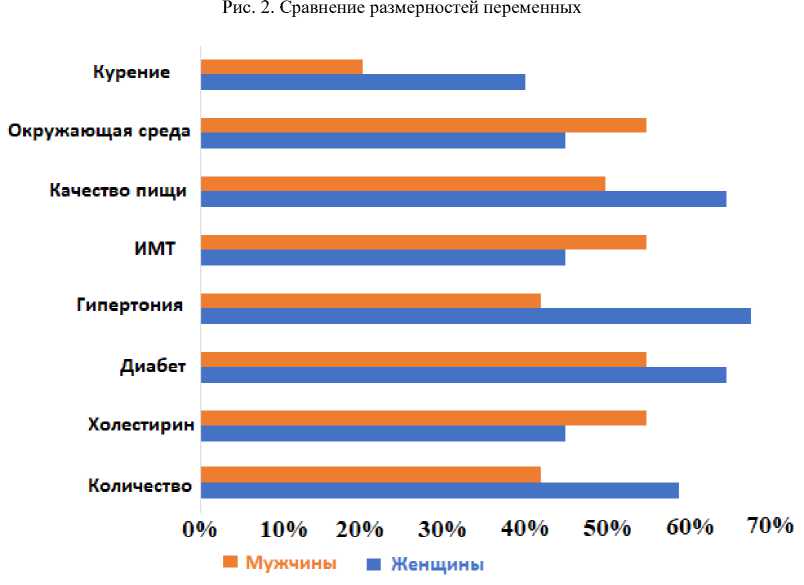
Рис. 3. Сравнение факторов риска среди мужчин и женщин

были исключены. Столбцы, которые приводили бы к незначительным результатам, также были удалены. Причина всех этих исключений заключалась в том, чтобы удалить все шумы из данных, чтобы можно было получить наилучшие результаты.

Результаты и обсуждение

В табл. 1 а и 2 а (см. Приложение) представлены корреляции между преобразованными переменными. С помощью анализа соответствия были выбраны высококоррелированные переменные (возраст, курение, пол, уровень холестерина, ожирение, гипертензия и инфаркт миокарда). Визуализация результатов представлена на рис. 2.

На рис. 3 серия двойных горизонтальных гистограмм сравнивает две серии данных: количество мужчин и женщин, показывающих разные факторы риска ишемической болезни сердца между полами. Оранжевые столбцы представляют количество мужчин по сравнению с синими столбцами для количества женщин с фактором риска, и хорошо видно, что женщины подвержены более высокому риску развития болезни [17].

Следующим шагом является выполнение лог-линейного анализа данных и выбор наиболее подходящей модели. Был выполнен многократный тест лог-линейного анализа по семи переменным (возраст, курение, ожирение, уровень холестерина, пол, гипертония и инфаркт миокарда).

В табл. 3 и 4 (см. Приложение) используется хи-квадрат отношения правдоподобия G ², чтобы увидеть, является ли модель статистически значимой. Для членов первого и более высокого порядка значимость получилась G ² = 3016,868 и 2756,597 соответственно. Аналогично G ² = 40,783 и 35,417 отображают значимость членов четвертого и пятого порядков. Поскольку в таблице всего пять факторов, то G ² = 5,366 представляет значимость пятистороннего взаимодействия. Можно сделать вывод, что интерпретация уровня значимости должна производиться с учетом размера выборки; чрезвычайно малые значения этой статистики указывают на то, что модель не соответствует данным.

Наблюдая за уровнями значимости ( P -значение), приведенными в табл. 4, можно заметить, что максимальный порядок значим. Также можно показать, что разница между таблицами 2 и 3 (см. Приложение) (для оценки гипотезы о влиянии данного фактора) одновременно равна нулю. Поскольку хи-квадрат Пирсона не может быть дифференцирован таким образом, показаны только тесты хи-квадрат отношения правдоподобия ( G ²). Эти тесты показывают значимость всех тестов в указанном порядке.

Они подтверждают вывод, сделанный из табл. 3 (см. Приложение), что 3-сторонние и 4-сторонние члены не значимы, в отличие от двусторонних и односторонних взаимодействий между факторами. Таким образом, дела- ется вывод о рассмотрении членов второго порядка как наивысших, учет которых необходим в окончательной модели. В лог-линейном анализе изменение значения статистики хи-квадрат отношения правдоподобия при добавлении или удалении слагаемых из модели является индикатором их вклада.

В табл. 6 (см. Приложение) представлены результаты тестов частичной ассоциации до третьего порядка. Параметр хи-квадрат – это разница между статистикой отношения правдоподобия двух моделей. Достоверность этой процедуры зависит от того, что отношение правдоподобия более сложной модели не имеет значения. В табл. 3 частичный критерий хи-квадрат проверяет, является ли односторонний член значимым или учитывает все члены одного порядка. Следовательно, когда оба критерия (отношение правдоподобия и критерий Пирсона) значимы, можно справедливо утверждать, что факторы данного порядка необходимы.

Согласно результатам теста частичного хи-квадрата, было замечено, что курение, гипертония и сердечный приступ являются очень значимыми, и они представляют собой связь между всеми определенными переменными для развития ишемической болезни сердца. Из модели можно определить, что ишемическая болезнь сердца диагностируется у пациентов, страдающих гипертонией в сочетании с постоянным курением, и гипертония остается основной причиной сердечного приступа.

Анализ соответствия определяет иерархическую модель, как описано в уравнении (4). Данный анализ основан на статистике хи-квадрата Пирсона. Соответствующие полученные результаты представлены в таблице 6, демонстрирующие хорошее соответствие с данными для обоих методов: статистики хи-квадрата Пирсона и ее альтернативы – статистического критерия отношения правдоподобия хи-квадрата. На рис. 4 показано графически различие между ре-зультатами двух методов (так называемые. скорректированные остатки). Данные выглядят нормально распределенными, поскольку точки хо-

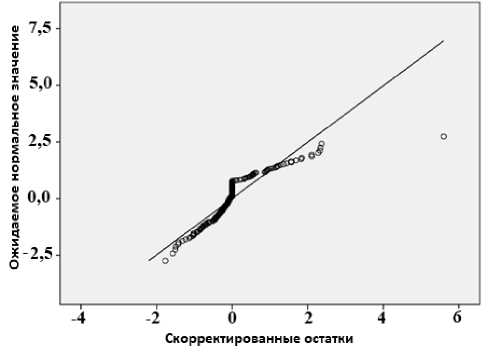
Рис. 4. График вероятности скорректированных остатков значения (ось Oy ) должны образовывать приблизительно угол 45°, что и показано на рис. 4.

рошо ложатся на диагональ. В модели с хорошей аппроксимацией остатки будут нормально распределены, причем большинство остатков близко к нулю. Скорректированные невязки (ось Ox ) и ожидаемые значения (ось Oy ) должны образовывать приблизительно угол 45°, что и показано на рис. 4.

Заключение

В этом исследовании был представлен объединенный подход двух статистических методов, включая анализ множественных соответствий и лог-линейный анализ. Как анализ множественных соответствий, так и лог-линейный анализ оказались наиболее подходящей моделью при одновременном использовании, что доказано графическим представлением данных. Используя анализ множественных соответствий [24], можно сократить количество интерактивных терминов и хорошо отобразить наши данные, что было бы полезно на этапе лог-линейного анализа.

Лог-линейный анализ можно использовать для анализа взаимосвязи между двумя категориальными переменными (см. табл. 5 в Приложении). Они чаще используются для оценки многомерных таблиц, которые включают три переменные или более. Все переменные, исследуемые лог-линейным анализом, рассматриваются как «переменные отклика». Другими словами, не делается различия между независимыми и зависимыми переменными. Следовательно, лог-линейный анализ только демонстрирует связь между переменными.

В лог-линейном анализе, если мы переходим к взаимодействиям более высокого порядка, ожидаемые частоты ячеек должны быть больше единицы. При невыполнении этого требования частота ошибок типа I (ложное срабатывание, т.е. когда мы отклоняем истинную гипотезу) обычно не увеличивается.

Если имеется значительный член взаимодействия, нет необходимости рассматривать члены более низкого порядка. Однако интерпретация терминов более высокого порядка необходима, чтобы избежать ошибки, возникающей из-за возможности зависимого кодирования и введения в заблуждение с помощью терминов более низкого порядка. Члены высшего порядка в лог-линейных моделях соответсвуют так называемой мини- мальной достаточной статистике, которая является маргинальной. В этом случае термин высшего порядка представляет собой трехстороннюю ассоциацию, и у нас есть ассоциация трех случайных величин и так далее.

Вот некоторые ключевые выводы нашей работы.

• •    Ишемическая болезнь сердца часто ошибочно относится исключительно к мужчинам, но наше исследование показало, что женщины подвергаются более высокому риску стать потенциальными жертвами, чем мужчины.

• •    Судя по медицинской литературе, чем мы старше, тем уже наши кровеносные сосуды становятся более жесткими, более суженными и менее эластичными. Все эти факторы могут привести к гипертонии. Следовательно, пожилые женщины более подвержены ишемической болезни сердца.

• •    В соответствии со всеми вышеупомянутыми факторами, гипертония была худшим последствием из всех. Гипертония по-разному влияет на сердце пациента. Например, это может вызвать гипертрофию желудочков, повлиять на координацию между правой и левой стороной сердца. Гипертония также является самым смертельным последствием ишемической болезни сердца.

• •    Отсутствие физической активности также является значительным фактором ишемической болезни сердца.

Можно сделать вывод, что анализ множественных соответствий в данном случае показал высокую эффективность, поскольку ассоциация между переменными достаточно устойчивая. Мы надеемся, что наш подход будет полезен не только для Пакистана, но также для Канады или России или любой другой страны в мире, поскольку эта болезнь становится всемирной проблемой в условиях глобализации. Мы также планируем получить данные у пациентов с ишемической болезнью сердца и людей, у которых есть лишь некоторые незначительные симптомы ишемической болезни сердца, а затем сравнить результаты и более точно подтвердить наши выводы.

Приложение

Таблица 1а

Влияние привычек питания на возраст

Краткое описание модели
Размерность	Альфа Кронбаха	Различия
		всего (собственные значения)	инерция
1	0,658	2,111	0,422
2	0,551	1,788	0,358
Всего	1,209	3,899	0,780
Среднее значение	0,605	1,950	0,390

Таблица 1б

Корреляции преобразованных переменных, связанных с типом питания и ожирением

Параметр	Возраст	Потребление фруктов	Употребление газированных напитков	Потребление мяса	Фастфуд	Ожирение
Возраст	1,000	-0,023	0,167	0,039	0,277	0,104
Потребление фруктов	-0,023	1,000	-0,013	-0,036	0,052	0,057
Употребление газированных напитков	0,167	-0,013	1,000	0,089	0,264	0,127
Потребление мяса	0,039	-0,036	0,089	1,000	0,086	0,162
Фастфуд	0,277	0,052	0,264	0,086	1,000	0,085
Ожирение	0,104	0,057	0,127	0,162	0,085	1,000
Размерность	1	2	3	4	5	6
Собственные значения	1,506	1,032	0,958	0,825	0,680	0,124

Таблица 2a

Влияние всех переменных по отношению к возрасту

Краткое описание модели
Размерность	Альфа Кронбаха	Различия
		всего (собственные значения)	инерция
1	0,737	2,969	0,297
2	0,682	2,587	0,259
Всего	1,419	5,555	0,556
Среднее значение	0,710	2,778	0,278

Таблица 2б

Корреляции трансформированных величин в зависимости от возраста

Параметр	Возраст	Образо-ваие	Потребление фрутов	Употребление газирован-ных напитков	Потребление мяса	Качество еды	Фастфуд	Окружающая среда	Курение
Возраст	1,000	0,104	-0,025	0,174	0,045	-0,031	0,260	0,101	0,085
Образование	0,104	1,000	0,118	-0,084	-0,028	-0,018	-0,097	0,108	0,143
Ожирение	0,111	0,051	0,054	0,127	0,241	0,018	0,087	0,164	0,108
Потребление фруктов	-0,025	0,118	1,000	-0,018	-0,090	0,043	-0,056	-0,028	0,139
Употребление газированных напитков	0,174	-0,084	-0,018	1,000	0,065	-0,031	0,261	0,140	-0,032
Потребление мяса	0,045	-0,028	-0,090	0,065	1,000	-0,009	0,082	0,009	0,069
Качество еды	-0,031	-0,018	0,043	-0,031	-0,009	1,000	-0,056	0,042	-0,039
Фастфуд	0,260	-0,097	-0,056	0,261	0,082	-0,056	1,000	-0,020	0,133
Окружающая среда	0,101	0,108	-0,028	0,140	0,009	0,042	-0,020	1,000	0,081
Курение	0,085	0,143	0,139	-0,032	0,069	-0,039	0,133	0,081	1,000
Размерность	1	2	4	5	6	7	8	9	10
Собственные значения	1,696	1,349	1,068	1,005	0,910	0,847	0,719	0,671	0,601

Таблица 3

Множественный тест между диагностированными заболеваниями у респондентов со всеми переменными

Порядок членов	Степени сво боды	Отношение правдоподобия		Статистика Пирсона
		хи-квадрат	P -значение	хи-квадрат	P -значение
1 и выше	959	3016,868	0,000	16315,590	0,000
2 и выше	946	260,271	1,000	349,202	0,856
3 и выше	878	109,743	1,000	135,678	0,889
4 и выше	692	40,783	1,000	34,838	0,945
5 и выше	403	5,366	1,000	4,114	0,9555

Таблица 4

Множественный тест между диагностированными заболеваниями у респондентов с ограниченным набором переменных

Порядок членов	Степени сво боды	Отношение правдоподобия		Статистика Пирсона
		хи-квадрат	P -значение	хи-квадрат	P -значение
1 и выше	959	3016,868	0,000	16315,590	0,000
2 и выше	946	260,271	1,000	349,202	0,856
3 и выше	878	109,743	1,000	135,678	0,889
4 и выше	692	40,783	1,000	34,838	0,945
5 и выше	403	5,366	1,000	4,114	0,9555

Таблица 5

Согласование переменных для выбора модели

Тесты согласия
	Хи-квадрат	Степени свободы	P -значение
Хи-квадрат отношения правдоподобия	66,263	892	0,726
Хи-квадрат Пирсона	62,190	892	0,456

Таблица 6

Частично ассоциированные переменные

Переменная	Степени свободы	Частный критерий хи-квадрат	P -значение
A	4	1506,434	0,000
S	2	91,033	0,000
C	1	79,409	0,000
O	3	1014,502	0,000
D	1	3,423	0,064
H	1	3,089	0,079
GA	4	0,000	1,000
GS	2	54,461	0,000
AS	8	0,000	1,000
GC	1	0,949	0,330
AC	4	0,000	1,000
SC	2	5,413	0,067

Продолжение табл. 6

Переменная	Степени свободы	Частный критерий хи-квадрат	P -значение
GO	3	2,994	0,393
AO	12	0,000	1,000
SO	6	21,859	0,001
CO	3	2,267	0,519
GD	1	0,779	0,377
AD	4	0,000	1,000
SD	2	33,781	0,000
CD	1	1,559	0,212
OD	3	2,462	0,482
GH	1	0,001	0,980
AH	4	0,000	1,000
SH	2	0,831	0,660
CH	1	0,021	0,886
OH	3	2,537	0,469
DH	1	2,689	0,101
GAS	8	0,000	1,000
GAC	4	0,000	1,000
GSC	2	1,630	0,443
ASC	8	0,000	1,000
GAO	12	0,000	1,000
GSO	6	4,508	0,608
ASO	24	0,000	1,000
GCO	3	5,720	0,126
ACO	12	0,000	1,000
SCO	6	2,688	0,847
GAD	4	0,000	1,000
GSD	2	8,200	0,017
ASD	8	0,000	1,000
GCD	1	2,777	0,096
ACD	4	0,000	1,000
SCD	2	7,504	0,023
GOD	3	10,107	0,018
AOD	12	,000	1,000
SOD	6	4,779	0,572
COD	3	1,822	0,610
GAH	4	0,000	1,000
GSH	2	2,645	0,266
ASH	8	0,000	1,000
GCH	1	0,352	0,553
ACH	4	0,000	1,000
SCH	2	0,755	0,686
GOH	3	0,617	0,892

Окончание табл. 6

Переменная	Степени свободы	Частный критерий хи-квадрат	P -значение
AOH	12	0,000	1,000
SOH	6	6,185	0,403
COH	3	1,098	0,778
GDH	1	2,712	0,100
ADH	4	0,000	1,000
SDH	2	9,254	0,010
CDH	1	,204	0,651
ODH	3	0,182	0,980

616 p.

correspondence analysis and log-linear analysis // Applied Statistics. – 1989. – Vol. 38, no. 2. – P. 249–292.

– New York: Academic Press, 1964. – 708 p.

– Vol. 10. – P. 1–8.