Использование быстрого преобразования Фурье в базисах Уолша на основе дискретно-экспоненциальной функции Виленкина-Кристесона

Базисы Уолша могут быть использованы для синтеза алгоритмов быстрого преобразования Фурье (БПФ) [1]. Причем, поскольку базисы Уолша являются частным случаем базисов Виленкина-Кристенсона, схема построения графов БПФ в базисах Уолша остается такой же, как и при построении графов БПФ в базисах Виленкина-Кристенсона [2]. При этом основанием базиса функций Уолша всегда является число m=2.

Рис. 1. Граф 16-ти точечного БПФ в базисе Виленкина-Кристенсона

Рассмотрим случай 8-ми точечного преобразования Фурье в базисе функций Уолша. При этом параметр n системы функций будет равен трем (23=8). Матрица Уо-лша-Адамара восьмого порядка представ- ляет собой третью кронекеровскую сте пень матрицы дискретно экспоненциальной функции Е2

ь =[01] (1)

При этом фазовращающий множитель равен (2):

2п     2п

W = е~ = е^-~ = -1 (2)

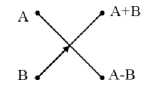
Рис. 2. Диаграмма «бабочка» для двухточечного преобразования Фурье

Сама матрица Уолша-Адамара выглядит так:

	Г0	0	0	0	0	0	0	0
	0	1	0	1	0	1	0	1
	0	0	1	1	0	0	1	1
Н 8 =	0	1	1	0	0	1	1	0	(3)
	0	0	0	0	1	1	1	1
	0	1	0	1	1	0	1	0
	0	0	1	1	1	1	0	0
	-0	1	1	0	1	0	0	1-

Синтезируем граф БПФ в базисе Уол-ша-Адамара Н8, рисунок 3. На входы графа на рисунке 1 отсчеты входного сигнала поступают в двоично-инверсной последовательности. Для того, чтобы преобразовать этот граф в граф БПФ в базисе Уол-ша-Пели Р8, необходимо провести m- ичную инверсию номеров отсчетов входного сигнала. Поскольку в данном случае m=2, то инверсия представляет собой двоичную инверсию, которая восстанавливает натуральную последовательность отсчетов входного сигнала (рис. 4).

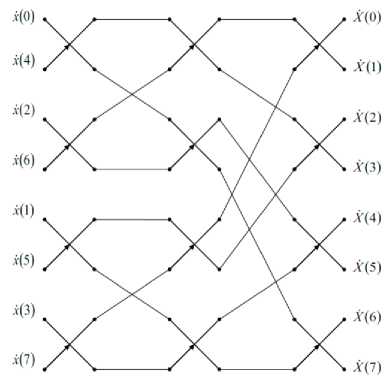
Рис. 3. Граф 8-ми точечного БПФ в базисе Уолша-Адамара

Матрица базисной системы Виленкина-Кристенсона - Пели Р₈ выглядит так (4):

^ 8 =

⁰ 0 -0

0 0

1 0

1 0

1 0

1 0

1 0

1 0

1 0

1 0

0-

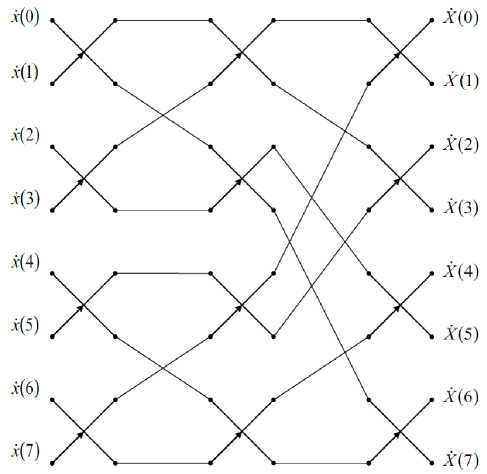
Рис. 4. Граф 8-ми точечного БПФ в базисе Уолша-Адамара

Легко проверить, что граф (рис. 3) соответствует матрице (3), в то время как граф (рис. 4) соответствует матрице (4). Графы БПФ в системах Уолша могут быть построены с помощью индикаторных матриц так, как это описано в подразделе, посвященном БПФ в дочерних базисах Виленкина-Кристенсона.

Если N - это m-рациональное число, то количество элементарных графов преобразований (процессоров БПФ в базисе дискретно-экспоненциальной функции с m входами) в графах БПФ в базисах дискретно-экспоненциальной функции Виленкина-Кристенсона совпадает [3]. Соответственно, совпадает и количество умножений чисел на степень фазовращающего множителя. При этом все элементарные графы, составляющие схему БПФ в базисе дискретно-экспоненциальной функции, можно разделить на две группы:

• 1)    Состоящая из элементарных графов, коэффициенты которых повторяют коэффициенты элементарных графов схемы преобразования в базисе Виленкина-Кристенсона;

• 2)    С отличающимися коэффициентами.

Если элементарные графы второй группы будут требовать больше машинного времени, чем графы первой группы, БПФ в базисе Виленкина-Кристенсона будут проходить быстрее, чем БПФ в базисе дискретно-экспоненциальной функции [4]. При этом выигрыш будет зависеть от соотношения между количествами графов в первой и второй группах, а также от соотношений времени выполнения этих графов. Проиллюстрируем описанную ситуацию на примере графов БПФ в базисах дискретно-экспоненциальной функции и Уолша при N=8. Рассмотрим рисунок 5.

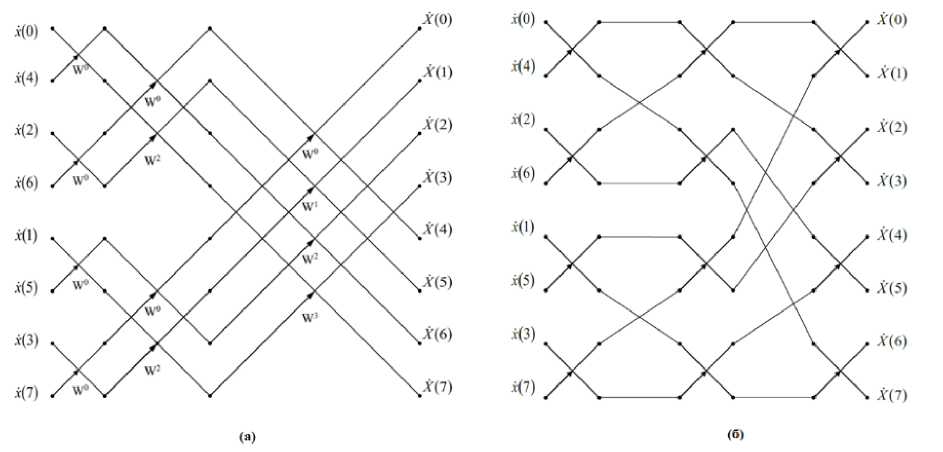
Рис. 5. а) Граф 8-ми точечного быстрого преобразования Фурье в базисе дискретноэкспоненциальные функции; б) Граф 8-ми точечного БПФ в базисе Уолша-Адамара

Видно, что к первой группе относятся те двухвыходные процессоры БПФ (диаграммы "бабочка"), при которых имеется коэффициент W0 (первый этап БПФ); ко второй группе - "бабочки" второго и третьего этапа преобразований, содержащие иррациональные коэффициенты. Если для выполнения графов первой группы требуются только операции сложения, то графы второй группы требуют выполнения умножения иррациональных чисел. Оценим соотношение между количеством тп-1(1 + - + Д т т2

членов этих двух групп для общего случая. Пусть размерность БПФ составляет N = т^п . Первый этап преобразований в базисе дискретно-экспоненциальной функции состоит из т^п-1 элементарных графов первой группы. Во втором этапе к первой группе принадлежит каждый из m графов, на третьем - каждый и m², на четвертом -каждый из m³ и т. п. Вычислив сумму этой геометрической прогрессии приходим к результату (5):

• 1  \   т^п-1 — 1

• ^{+  +} т^п-1) т — 1                 (5)

При этом общее количество элементарных графов в схеме БПФ составляет т^п 1 п . Соответственно, относительное количество элементарных графов первой группы составит:

,       т^п 1 -1

К = ------—

• ¹    (т-1)т^п 1 п

Относительное количество элементарных графов второй группы равно:

^К 2

—

т^п 1 -1

(т-1)т^п 1 п

Оценим время, необходимое для выполнения графов обеих групп. Обозначим через t1 время, необходимое для выполнения графов первой группы, через t2 - время для графов второй группы, через K - количество элементарных графов в схеме БПФ [5]. Тогда общее время на выполнение БПФ будет равно:

Т = K(t 1 k 1 + t 2 k 2 )

При m=4 элементарный граф БПФ в базисе Виленкина-Кристенсона представлен на рисунке 6. Выполнение этого графа есть умножение на матрицу размером 4x4 (рисунок 6):

I

1  1

j ^-1 -1  1

-j -1

-I

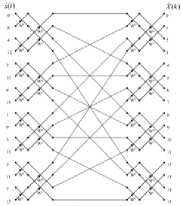
Рис. 6. Граф 16-ти точечного БПФ в базисе Виленкина-Кристенсона -Кронекра Н2

Для выполнения умножения на такую матрицу (9) вектора-столбца, состоящего из 4-х комплексных элементов, требуется выполнить 24 операции сложения действительных чисел. Обозначим через t+ время, необходимое для выполнения сло- жения, а через tx - время умножения. При этом t1 = 24t+. Общее время выполнения БПФ в базисе Виленкина-Кристенсона составит:

^ Виленкина-Кристенсона    24Kt + (10)

Графам второй группы соответствует матрица преобразования:

I

ИMZ

W2q и44

W6qи

1 и/³ ^

W6q и244

l

где коэффициент q зависит от размерности БПФ и номера этапа преобразования. В общем случае выполнение такого графа потребует 36 операций умножения и 42 операции сложения. Соответственно, t2 = 36tx + 42t+. А общее время выполнения операции БПФ в базисе дискретноэкспоненциальной функции составит

Тдискретно-экспоненциальной функции

= K(24t₊k 1 + (36t_x + 42t₊)k 2 ) (12)

Учитывая (6) - (8), (9), (11) приходим к выражению для оценки выигрыша времени при переходе от базиса дискретно- экспоненциальной функции в базис Ви ленкина-Кристенсона с основанием m=4:

^ = 1 + (1

-

4n-1-1

3*4п-1П

\ / 6G+31 +

4tx   .

В современной вычислительной технике при выполнении операции умножения с фиксированной точкой считается, что tx = 5t+, для операций с плавающей точкой - tx = t+. Учитывая эту оценку, перепишем выражение (12):

для умножения с плавающей точкой:

п-1

f = 1 + 2.25(1——— 1 )          (13)

3*4п-1П для умножения с фиксированной точкой

< = 1 + 8.25(1— ^ч¹)              (14)

3*4п-1П

Зависимость выигрыша в объеме вычислений при переходе от БПФ-ДЭФ к БПФ- Виленкина-Кристенсона от порядка БПФ при умножении с плавающей точкой показана на рис. Максимально возможное

(при п ^ от ) значение ^ составляет 3.5, реально достижимое - около трех. Зависимость выигрыша от размерности БПФ представлена на рисунке 7.

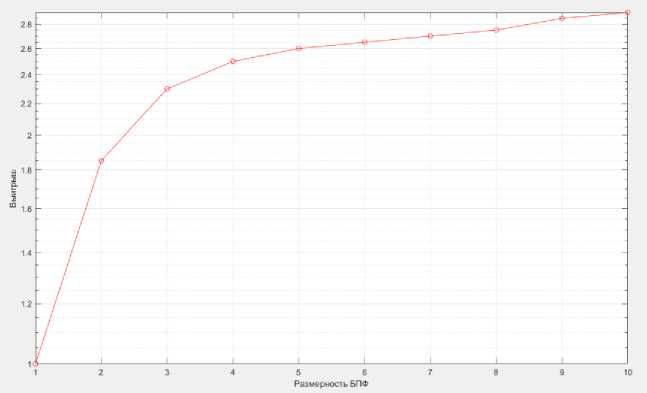
Рис. 7. Зависимость выигрыша от размерности БПФ

Если алгоритм БПФ в базисе Виленкина-Кристенсона будет учитывать факторизацию матрицы (9), то конечное выраже- ние для оценки выигрыша в быстродействии в случае умножения с плавающей точкой примет вид (15):

2^я - ¹ — 1

< = 1 + 4(1—         )                (15)

у 3 * 2^я 1 П/

При этом максимально возможное значение ( составит 5. Реально достижимое его значение будет составлять около 4. При использовании умножения с фиксированной точкой выигрыш составит около 11.

Заключение

Структуры полученных графов по сложности не отличаются от графов быстрого преобразования Фурье в базисах дискретно-экспоненциальной функции, при этом вычисления спектра в базисе Вилен- кина-Кристенсона требует меньше затрат машинного времени на вычисления (скорость обработки растет на порядок). Данное свойство может быть использовано для реализации устройств, оценивающих частоту принятого дискретноэкспоненциального сигнала в базисе Виленкина-Кристенсона, обладающего более высоким быстродействием, чем аналогичное устройство, работающее на базисе дискретно-экспоненциальной функции.