Использование эффекта азимутального рассеяния электромагнитных волн метаструктурой на основе элементов Телледжена в прикладных задачах электродинамики

В 1948 г. Телледжен [1] высказал предположение, что, объединяя электрический и магнитный диполи в единый элемент, можно получить новый тип композитной среды с неизвестными ранее свойствами. Однако вплоть до настоящего времени вопросы создания и корректного описания сред на основе элементов, названных элементами Телледжена [2], являются предметом ожив- ленных дискуссий среди ученых многих стран мира.

Подобные среды и их сложные композиционные соединения представляют значительный практический интерес в связи с активным исследованием и разработкой мета- и наноструктур. Сами элементы Телледжена по сути являются ки-ральными за счет своей зеркально асимметричной формы. Можно считать, что в этом случае киральность является физической [3], так как она создается не формой структуры в целом, а формами находящихся в ней элементов.

При теоретическом исследовании свойств структур с киральными включениями изначально основной упор делался на изучение дифракции плоских электромагнитных волн на таких рассеивателях. Этот интерес связан прежде всего с возможностью применения метаструктур для решения различных прикладных задач электродинамики.

Метаструктуры в технике и технологиях телекоммуникаций

Одним из весьма интересных свойств, характерных для метаструктур на основе элементов Телледжена, является возможность изменения направления потока электромагнитного излучения, падающего на плоский слой метаматериала. По сути, каждый такой элемент, (см. рис. 1а) представляет собой электрически малую рамку круглой либо прямоугольной формы, в зазор ко- элемент Телледжена

модифицированный элемент Телледжена

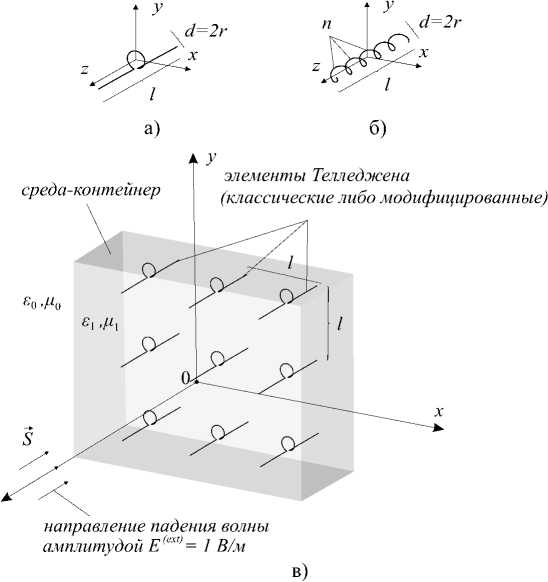
Рис. 1. 3D-киральные элементы Телледжена и метаструктура на их основе а); б) – виды элементов; в) – геометрия метаструктуры и модель возбуждения

торой включен симметричный электрический вибратор.

Особенностью метаматериала является то, что при облучении его полем электромагнитной волны, как показано на рис. 1, основная энергия волны не проходит сквозь метаматериал и не отражается назад, а рассеивается структурой в азимутальной плоскости, формируя волны, распространяющиеся параллельно ее поверхности. При этом процесс переизлучения осуществляется вибратором, который возбуждается полем, наводимым в рамке.

Следует отметить, что в случае классического элемента Телледжена рамка сосредоточена в одной плоскости. Однако тот же эффект азимутального рассеяния поля может быть достигнут, если рамка окажется не сосредоточенной, а равномерно распределенной по всей длине вибратора, формируя цилиндрическую спираль. Будем называть такой элемент модифицированным элементом Телледжена. Вид метаматериала на основе подобных спиральных элементов представлен на рис. 1б.

В настоящей работе установлено, что электродинамические характеристики классического и модифицированного элементов Телледжена с практической точностью совпадают.

Эффект бокового рассеяния электромагнитного поля может быть широко использован при создании различных радиотехнических устройств и структур. Ниже перечислены некоторые области, применение метаструктур в которых может, по мнению авторов работы, дать наиболее значимые практические результаты.

Энергосберегающие технологии в телекоммуникациях. Весьма актуальной задачей в настоящее время является создание устройств, способных накапливать (концентрировать) энергию электромагнитных волн, поступающую из внешней среды, для последующего ее преобразования в удобный вид и использования в различных полезных целях, в том числе для функционирования самого электронного устройства. Если устройство использует в работе радиоинтерфейс (сотовая связь GSM/DCS/UMTS, технологии WiFi, WiMAX, и мн. др.), актуальность задачи еще более возрастает. Для ее решения авторами предлагается киральная метаструктура (слой), способная концентрировать рассеянное электромагнитное излучение ДМВ, СМВ и ММВ из вне- шней среды – так называемый концентратор, которая может быть дополнена устройством съема и преобразования энергии. Необходимо отметить, что особенно важной задачей в настоящее время является возможность сбора энергии квазиопти-ческого (инфракрасного, ИК) и оптического – видимого диапазонов. Это связано с тем, что на эти диапазоны приходится основная доля энергии солнечного спектра. Однако солнечные элементы с приемлемым КПД (до 40-50%) на сегодняшний день весьма дороги, что не дает возможности повсеместно использовать «солнечные коллекторы». Авторами сделано предположение, что применение киральных концентрирующих структур в перспективе возможно будет обобщить на оптический диапазон, что позволит использовать солнечные элементы для приема и преобразования не рассеянного, а концентрированного излучения, таким образом уменьшив их количество в «солнечном коллекторе» на несколько порядков, примерно во столько же раз уменьшив стоимость изделия. Для реализации оптического концентратора предполагается использовать структуры на основе углеродных нанотрубок в форме цилиндрических спиралей (графен) [4].

Задачи снижения радиолокационной заметности и улучшения защитных функций объектов. Снижение локационной заметности объектов в радиодиапазоне (СВЧ, КВЧ) на протяжении многих лет является одной из основных стратегических задач, стоящих перед научно-производственным комплексом РФ. При этом к разрабатываемым конструкциям зачастую предъявляются довольно жесткие технологические требования: широко-полосность, малый уровень обратного отражения (как правило, меньше –20 дБ) при хороших массогабаритных характеристиках. Среди последних особенно важными являются малый вес и т.н. конформность, предполагающая размещение их на поверхностях практически произвольной формы и кривизны. Авторами работы предлагается использовать для решения задачи киральную метаструктуру со свойствами бокового рассеяния поля. При необходимости структура может быть реализована в виде конформного слоя, имеющего малый вес и хорошие ценовые характеристики. Кроме того, структура может быть использована для защиты объектов от направленного и рассеянного воздействия радиоизлучений СВЧ- и КВЧ-диапазонов, то есть может выполнять защитные функции.

Использование подобных метаструктур в технике и технологиях телекоммуникаций, по мнению авторов, позволит существенно оптими- зировать технические и технологические характеристики разрабатываемых и существующих электронных устройств.

Киральные биизотропные метаструктуры на основе объемных тонкопроволочных спиралей

Одним из наиболее часто исследуемых ки-ральных элементов является тонкопроволочная спираль – модифицированный элемент Теллед-жена, изображенный на рис.1б. В большинстве работ по электродинамике киральных метаматериалов используется бездисперсионная модель среды, то есть предполагается отсутствие зависимости материальных параметров (диэлектрической и магнитной проницаемостей и относительного параметра киральности) от частоты. Однако такая модель не может быть использована при разработке и технической реализации образцов киральных метаматериалов, которые принципиально обладают резонансными свойствами.

Любой киральный метаматериал представляет собой совокупность среды-контейнера, в которой размещаются проводящие элементы зеркально асимметричной формы (классические либо модифицированные элементы Телледжена и т.п.).

Для описания электромагнитных свойств ки-рального метаматериала обычно используются материальные уравнения, согласно формализму Линделла-Сиволы [5-9]:

D = sE - i%H,

-      -      -                  (1)

В = pH + i/E,

где £ И // – относительные диэлектрическая и магнитная проницаемости киральной среды; X – относительный параметр киральности.

Уравнения (1) описывают обобщенную ки-ральную среду без конкретизации типа тонкопроволочных киральных элементов. Дисперсионные зависимости диэлектрической проницаемости и параметра киральности определяются из следующих соотношений [10]:

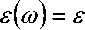
Pl

2         2 ’

(0^-0)

zM = ^0

c((Dq — (У²)

где £r – относительная диэлектрическая проницаемость среды-контейнера; ^0 и A – некоторые постоянные.

Для расчета резонансной частоты Юд можно воспользоваться следующим методом. На первом этапе спиральный элемент заменяется эквивалентной схемой, содержащей емкости (межвит-ковая емкость и емкость тонкой металлической проволоки) и индуктивность проводника в виде спирали. На втором этапе по формуле Томсона рассчитывается резонансная частота элемента:

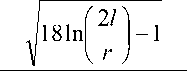
J^NR^-W ’

где ГИ / – радиус и длина проволоки; А¹ г – магнитная проницаемость среды-контейнера; N – число витков спирали; R – радиус витка.

Нормальными волнами кирального метаматериала являются волны с право-(ПКП) и левокруговыми (ЛКП) поляризациями, обладающие различными постоянными распространения:

^kR,L И = — U^R ± Z^b  (4)

с

где ^((у) и ^((у) определяются формулами (2) с учетом выражения для резонансной частоты (3). На рис. 2 приведен пример дисперсионных характеристик нормальных волн кирального метаматериала на основе тонкопроволочных элементов. Как видно из рис. 2, волны с право- и левокруговыми поляризациями испытывают явление бифуркации дисперсионных характеристик, причем степень дуплетного расщепления значительно больше вблизи резонансной частоты. Кроме того, можно отметить, что на частотах ниже резонансной фазовая скорость больше у волны ЛКП, чем у ПКП, а выше резонансной частоты – характер изменяется на противоположный.

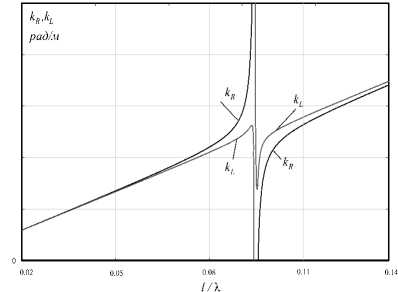
Рис. 2. Дисперсионные характеристики нормальных волн кирального метаматериала на основе объемных спиралей

В настоящей работе проведен электродинамический анализ свойств плоского метаматериала, состоящего из двух киральных слоев с различными значениями физических и геометрических параметров (см. рис. 3). Киральный слой представляет собой композиционную среду на основе двумерной матрицы проводящих киральных элементов в виде модифицированных элементов Телледжена, размещенной в магнитодиэлектрическом контейнере. Ориентация элементов случайная. Рассмотрено падение плоской электромагнитной волны с перпендикулярной поляризацией на двухслойную киральную структуру. Целью работы являлась оптимизация геометрии задачи с целью одновременной минимизации модулей коэффициентов отражения и прохождения в некотором интервале частот.

Задача решалась методом частичных областей и была сведена к системе линейных алгебраических уравнений относительно неизвестных амплитудных коэффициентов отражения и прохождения основной и кроссполяризованной компонент поля.

Выражения для продольных составляющих векторов электромагнитного поля в киральных слоях имеют вид [5-9]:

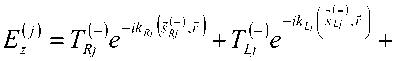
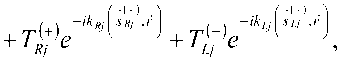
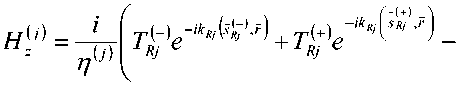
-Т^е*^^ __Т^_е'^к^^ , (5)

где s^tj ={sin^ _L -cos^ _L J – единичные векторы, вдоль которых распространяются преломленные в j -ый слой волны; ^Й 4sine_RLi,cose_RL^ – единичные векторы, вдоль которых распространяются отраженные от следующей области волны; 6r,L – углы, которые векторы Sr? ^и #^} образуют с положительным направлением оси Oy ; 77^(/) = Hj = ^.//r, – характеристическое сопротивление j -го кирального слоя; ^kR,Lj ^=koU^j-X? – постоянные распространения нормальных волн ПКП и ЛКП в j -ом киральном слое ( j = 2; 3).

Были подобраны значения физических и геометрических параметров киральных слоев 2 и 3 (см. таблицу 1), при которых исследуемая струк-

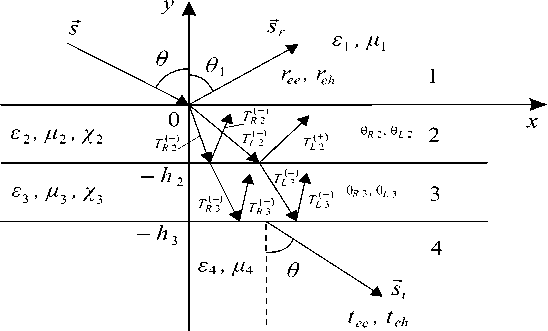
Рис. 3. Падение плоской электромагнитной волны на двухслойный киральный метаматериал (области 1 и 4 – диэлектрик, воздух, 2 и 3 – киральные слои на основе спиралей)

тура может одновременно выполнять функцию концентрации СВЧ энергии (^^° ’^ ^°Х а также обладать защитными свойствами (^^0 ) и свойствами малых отражений -^0 ).

На рис. 4 приведены частотные зависимости квадратов модулей коэффициентов отражения Гее И ^e для выбранных параметров структуры. В результате оптимизации был сделан вывод о том, что наиболее эффективно использование длинных растянутых спиралей с 2-3 витками, образующих один слой в контейнере. Кроме того, размеры спиралей были подобраны таким обра- зом, чтобы их резонансные частоты находились значительно ниже от предполагаемого рабочего диапазона концентратора. На рисунке приведена геометрия задачи и частотная зависимость квадратов модулей коэффициентов отражения и прохождения для случая нормального падения волны на метаструктуру. Как видно из рис. 4, в диапазоне выше 0.08//Я значения модулей коэффициентов отражения и прохождения не превышают 0,2; что позволяет использовать структуру в качестве концентратора СВЧ энергии и для других не менее актуальных задач. Энергия электромаг-

Таблица 1. Параметры киральных слоев

Параметры киральногослоя 2
Параметры контейнера
Re часть диэлектрической проницаемости контейнера	3,5
Im часть диэлектрической проницаемости контейнера	0,8
Re часть магнитной проницаемости контейнера	2,2
Im часть магнитной проницаемости контейнера	0,5
Толщина контейнера, мм	10
Параметры спиральных включений
Количество витков спирали	2
Радиус проволоки, мм	0,1
Радиус витка спирали, мм	2
Длина спирали, мм	3,5
Расстояние между соседними спиралями, мм	1,5
Циклотронная частота, ГГц	1

Параметры киральногослоя 3 Параметры контейнера Re часть диэлектрической проницаемости контейнера 3,5 Im часть диэлектрической проницаемости контейнера 0,2 Re часть магнитной проницаемости контейнера 13 Im часть магнитной проницаемости контейнера 0,1 Толщина контейнера, мм 3 Параметры спиральных включений Количество витков спирали 2 Радиус проволоки, мм 0,1 Радиус витка спирали, мм 2 Длина спирали, мм 3,4 Расстояние между соседними спиралями, мм 1,5 Циклотронная частота, ГГц 1,5 нитного поля концентрируется в метаструктуре или сосредоточена вблизи ее поверхности.

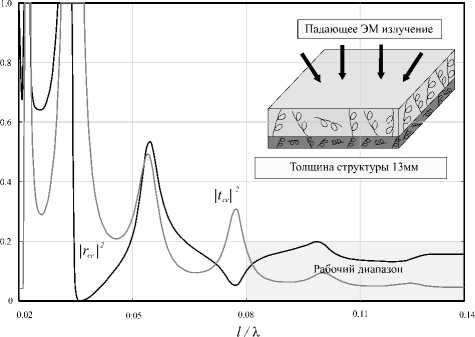
Рис. 4. Зависимости квадратов модулей коэффициентов отражения и прохождения от частоты при падении волны на двухслойный киральный метаматериал

Отметим, что рабочий режим метаструктуры сдвинут в сторону верхних частот, то есть расположен выше резонансной области.

Численный анализ бианизотропных метаструктур на основе элементов Телледжена

В предыдущем разделе были рассмотрены основные характеристики двухслойной биизот-ропной киральной метаструктуры с включениями в виде модифицированных элементов Тел-леджена со случайной ориентацией. В данном разделе задача обобщена на случай бианизот-ропной среды с ориентацией элементов ортогонально поверхности метаструктуры (вдоль оси ^Y В связи со сложностью построения строгой модели бианизотропной среды с киральными включениями авторы ограничились численным моделированием в пакете трехмерного электромагнитного анализа CST Microwave Studio (вычислитель Integral Equation solver). Проведено электродинамическое моделирование характеристик одиночного элемента Телледжена, а также матрицы элементов. Кроме того, проведена численная оптимизация геометрических размеров, формы элементов и расстояния между ними по критерию максимума бокового и минимума осевого рассеяния поля. Общая геометрия метаструктуры (слоя) на основе элементов Тел-леджена приведена на рис. 1в. Толщина слоя и длина элементов выбраны одинаковыми. Материальные параметры среды контейнера ЗДх, окружающего пространства ^0^0 (вакуум).

Рассмотрены два случая ориентации элементов в азимутальной плоскости XОY: для матриц <5x5 все элементы ориентированы зазорами к центру структуры. Для матриц размером <5x5 выбрана случайная ориентация элементов по азимуту. Такая модель выбрана для сохранения изотропного распределения поля рассеяния структуры в азимутальной плоскости: lE^)] = const. Кроме того, для максимального упрощения задачи были выбраны параметры среды-контейнера £"i ^o ’A ^o • В этом случае удобнее всего оценивать уровни поля бокового рассеяния структуры с помощью диаграмм направленности (рассеяния, ДР) в дальней зоне излучения, а также пробников поля.

Возбуждение структуры осуществляется полем плоской электромагнитной волны, имеющей правую круговую поляризацию. Поляризация волны совпадает с направлением намотки спиралей элементов. Амплитуда волны задана на поверхности структуры и составляет E = 1 В/м.

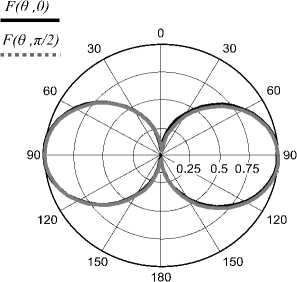
На рис. 5 показана нормированная диаграмма рассеяния (ДР) электрического поля в дальней

a)                                       6)

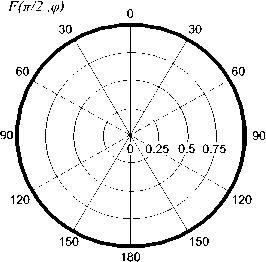
Рис. 5. Диаграммы рассеяния на элементах Телледжена: а) - меридианальные, б) - азимутальная

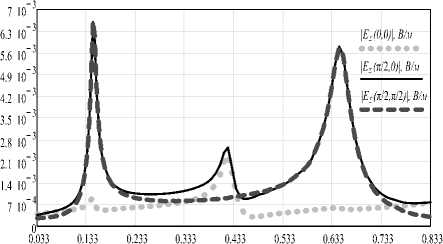
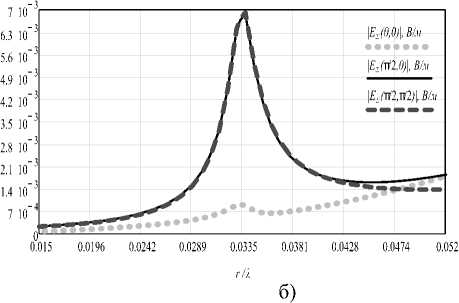
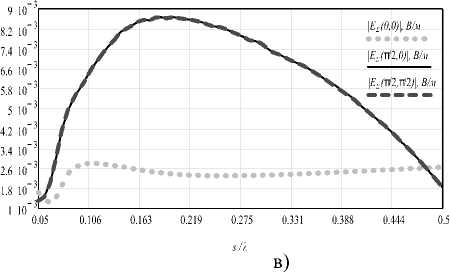
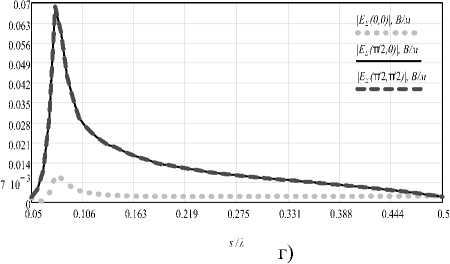
Рис. 6. Зависимости уровней бокового и осевого рассеяния по модулю электрического поля (геометрической суммы составляющих Е^ и Е_е) структуры от электрических размеров а) - от длины вибратора /, б) - от радиуса рамки г, (в) - от расстояния между элементами s при / = i^, г) - от расстояния между элементами s при / = / И

зоне структуры. Видно, что диаграмма по форме представляет собой тор, лежащий в плоскости XОY. Установлено, что ДР для одиночного элемента и матрицы 2×2…10×10 элементов практически полностью идентичны. Из полученных данных можно сделать вывод, что форма ДР либо не зависит от количества элементов матрицы, либо зависит весьма несущественно.

Рис. 6 представляет зависимости уровня поля рассеяния в боковом и осевом направлениях от размеров элементов и расстояния между ними. На рис. 6а приведены результаты оптимизации характеристик одиночного элемента Тел-леджена по длине электрического вибратора. Хорошо видно, что имеется две рабочие области, в которых боковое рассеяние максимально: /ИД =0.15, ДД=0.65, где /",_« = !; 2 – оптимальная длина вибратора в каждой из областей, ^0 – некоторая фиксированная длина волны в рабочей полосе ^^^/ Атах ^'min * Установлено, что перекрытие в полосе рабочих длин волн структуры ^D ^тах /Anin > ^^ ’ то есть структура является сверхширокополосной. Однако следует отметить, что КПД структуры, показывающий процент отбора энергии у падающей волны в полосе, весьма различен и обратно пропорционален длине волны Л. Пробники поля установлены на расстоянии h = 1 ОЯо от структуры.

На рис. 6б показаны результаты оптимизации одиночного элемента Телледжена от радиуса рамки. Отчетливо виден пик вблизи значения радиуса г/Л₀ = 0.0335, определяющий центр рабочей области. Рис. 6в иллюстрирует результаты оптимизации матрицы элементов Телледжена по расстоянию между элементами s для случая / = /⁽¹?- На рис. 6г представлено то же для ср . Оба рисунка содержат области оптимальных значений 1: $“р<,=М. для / = /.;', 4’А =0.075 для/,/И.

Выводы

Предложено использовать киральные метаструктуры на основе 3D-элементов Телледжена и спиральных элементов в качестве структур концентрации электромагнитной энергии СВЧ-, КВЧ-диа-пазонов, а также для снижения радиолокационной заметности объектов и защиты от внешних излучений. Показано, что элемент Телледжена может быть выполнен как с сосредоточенной в одной плоскости рамкой, так и с равномерно распределенной по длине симметричного вибратора. При этом электроди- намические характеристики элемента существенно не изменяются.

Установлено, что в определенных условиях для элементов Телледжена при возбуждении полем плоской электромагнитной волны характерно свойство бокового рассеяния электромагнитного поля, уровни которого, а также КПД структуры в целом (процент отбора энергии от волны) могут быть заданы на этапе разработки и оптимизации. Сделано предположение о возможности использования киральных метаструктур для концентрации энергии оптического и квазиоптического диапазонов волн.