Использование эффекта НТО для управления пространственным распределением излучения

Эффект нелинейного термического отражения (НТО), заключающийся в изменении коэффициента отражения за счет тепловой нелинейности при взаимодействии излучения с границей раздела сред, достаточно полно исследован теоретически и экспериментально [1-5]. При НТО легко реализуется гистерезисный режим отражения, а в интерферометрах с тепловой нелинейностью - бистабильный режим. НТО использовались для модуляции добротности резонатора [1,6], для создания оптических затворов [3] и оптических триггеров [5].

В работах [1,7] предложено использовать НТО для управления пространственным распределением излучения. Создание такого рода устройств является одной из важнейших задач адаптивной оптики и оптоэлектроники.

В настоящей работе приводятся точные решения двух наиболее важных случаев использования НТО для управления пространственным распределением излучения. Приведены также численные результаты расчетов транспарантов отражательного типа.

Показатель преломления изотропной среды при изменении ее температуры на ДТ и плотности на Др изменяется на величину

Ап = ^р дт + фт др'                                     (1)

Температура образующих границу раздела сред определяется системой уравнений теплопроводности, которая в достаточно общем случае радиальной симметрии имеет вид

Л ЭТа^г^ _ V2Ta(rfZft) = 2 i(r,t)R(T,p,t)e~oz;

а2 dt                          с                                                  (2)

В отличие от вышеуказанных работ рассмотрим трехмерную задачу в случае радиальной симметрии в приближении мгновенного распространения звука, т.е. для времен, больших 1/v  , где 1 - минимальный размер нагреваемой области. При з в этом показатель преломления определяется только температурой и (1) принимает более простой вид:

Дп = (^) ДТ,                                                                 (4)

т.е. показатель преломления в каждой точке определяется температурой. В том случае, когда температура мало изменяется на расстоянии порядка длины волны, что обычно соответствует реальной ситуации, коэффициент отражения описывается обычными формулами Френеля.

Рассмотрим случай стороннего нагрева (рис. 1), при котором изменение температурного рельефа, а следовательно и коэффициента отражения для пучка К, создается пучком Кг). При этом коэффициент отражения для греющего пучка 1(г) практически не изменяется с температурой вследствие падения излучения на границу под углом, близким к нормальному J1] .

В этом предположении R = 1.

• a)    I(r,t) = Е(г) • 6(t) (мгновенный нагрев).

Решение системы уравнений (2), связанных условиями (3)z было получено методом последовательного применения интегральных преобразований Лапласа с параметром s по времени t и Ханкеля с параметром g по радиусу г:

Ti,_a(r,Z,t) - T_if2L(r,z,s) - т_{1 /2LH}(E,z,s) е Yi,2.

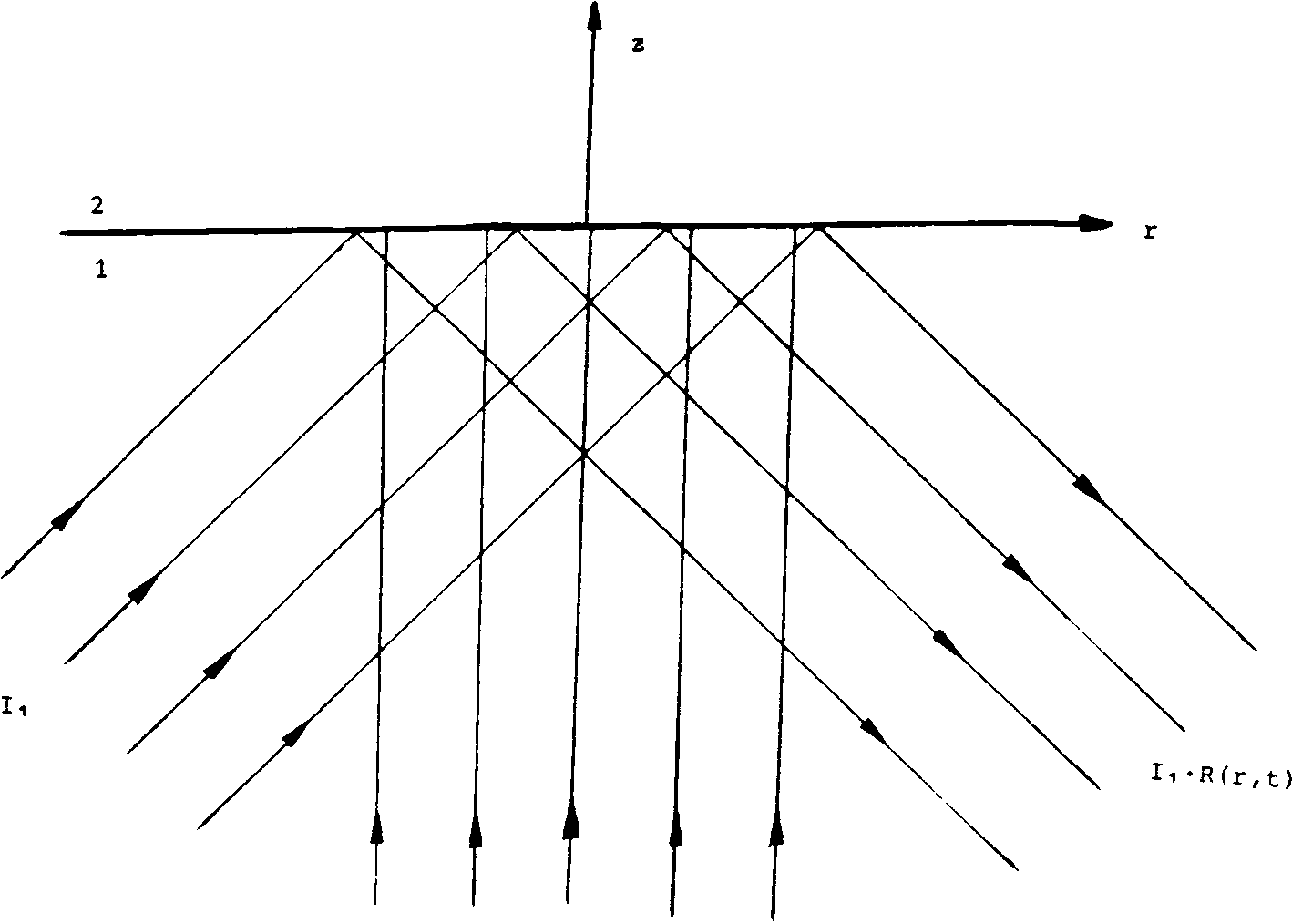
Рис. 1. Управление коэффициентом отражения излучения К с помощью излучения I(r,t) при отражении от границы раздела сред 1 и 2.

Поглощением обладает только среда 2

При этом система уравнений в частных производных для T(r,z,t) переходит в систему линейных дифференциальных уравнений для образов У1/2!

sY, - e~oz • Н = а1 (-E2Yi + |^-)

sYa = a, (-E2Ya + g^), связанных условиями

• Y₁(0) = Y₃(0); Y^(0) = ^ y^(0).

Решив эту систему и проведя обратное преобразование Ханкеля и Лапласа в точке z = 0, получим выражение для температуры границы:

T(r,t) = 7^  / ds / dE ^Н^ °^/§²+s/ai) Ip (Er)e^st            ,        ₍₅₎

ai(E2 + s/ai - а=) -(1 + ^ l/R^Sj^)

Ai у 5 * s / а2 ОО где H(g) = /Е(г)Io(Er)dr; Io - функция Бесселя. При ai,2 = а для гауссовского о распределения интенсивности

решение имеет вид:

_R пе~°^2а^ (p=+at)-i ^е —

^ехР [~ 2(^ + at)j '

Коэффициент отражения определяется из приведенного выражения для темпера туры г соотношения (4) и формул Френеля. На рис. 2 приведены распределения тем пературы по сечению в различные моменты времени для значений бугеровского затухания 0,1 см-1 и 30 см"1. В последнем случае динамика коэффициента отражения определяется в основном теплопередачей по нормали к границе и форма профиля коэффициента отражения практически не изменяется. При а = 4-Ю"3 см2/с, что соответствует реальным значениям, заметное изменение коэффициента отражения происходит при о = 0,1 см-1 за 10 с, а при о = 30 см-1 за Ю"2 с.

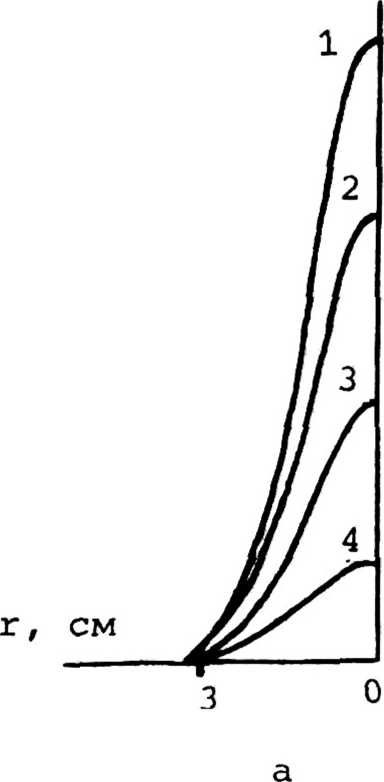
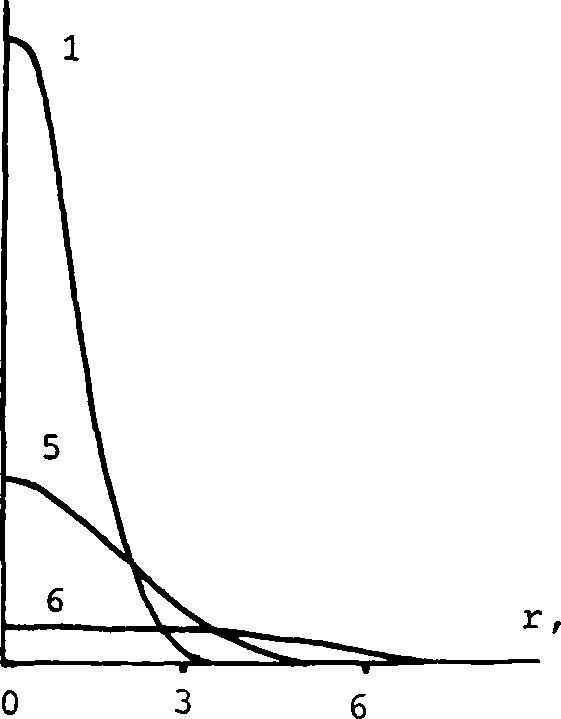
Рис. 2. Распределение температуры при различных значениях at и о для а = 4-10-3 см2/с:

• а)    о = 30 см~¹; 1) at = 0, 2) at = 10** см², 3) at = 10^-3 см²; 4) at = IO"² см²;

• б)    о = 0,1 см^-1: 5) at = 1 см²; 6) at = 10 см²

• 6)    I(r,t) = I (г) (стационарный нагрев) .

В стационарном случае производные по времени в (2) обращаются в нуль и начальные условия не существенны. Выражение для стационарного распределения температуры, полученное аналогично выражению (5) , имеет вид:

^{Т(г) =} a^Cl^/XJ ' 3^ I=(Er)dg откуда

Кг) = ^ d+X3Ai) /dEE=(E+a)lo(Er) / l0 (Er1) T(r')r'dr'.          <6>

Последнее выражение представляет собой решение "обратной” задачи - нахождение распределения интенсивности, при котором реализуется заданное распределение температуры Т(г). Интеграл (6) существует для широкого класса функций Т(г). Поскольку температура однозначно определяет коэффициент отражения, из существования (6) следует, что для осуществления транспаранта заданного профиля может быть подобрано необходимое распределение интенсивности греющего излучения.

Время установления стационарного распределения температуры определяется температуропроводностью а2 и геометрией. При большом поглощении это время порядка Гд/а2, где го - характерный радиус "мягкой" диафрагмы. Случай стационарного нагрева иллюстрируется на рис. 3, на котором приведены стационарные распределения коэффициента отражения при различных значениях мощности излучения, а также форма установившегося распределения температуры. Считалось, что S-поляризованное греющее излучение имеет гауссовский профиль, а угол его падения на границу раздела - 67°, что на 0,8° меньше угла полного внутреннего отражения.

Таким образом, эффект НТО предоставляет возможность создания транспаранта с любым заданным профилем пропускания и изменением этого профиля во времени. Полученные результаты легко обобщаются на случай интерферометра с тепловой нелинейностью.

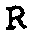
Рис. 3. Распределение коэффициента отражения и температуры при стационарном нагреве для гауссовского распределения I(г) (р = 1 см; о = 30 см-1) при различных значениях мощности греющего излучения: