Использование компьютерного моделирования для формирования профессиональных компетенций выпускников

Требования, предъявляемые в современном обществе к выпускникам вузов, изложены в Федеральном государственном образовательном стандарте (ФГОС), построенном на компетентностном подходе [1-2]. Этот подход предполагает увеличение роли проектной и научно-исследовательской работы в профессиональной деятельности выпускников математических направлений подготовки, связанных с информационными технологиями [3-7]. Реализация образовательных программ современных образовательных стандартов невозможна без применения технологий , использующих электронные образовательные средства [8-10,14-16]. Эта тенденция закреплена и в образовательных стандартах Нижегородского государственного университета им. Н.И. Лобачевского в области информационно-коммуникационных технологий  [11-12].  Вопросам использования информационных технологий в образовательном процессе посвящено много работ [14-20].

Выпускники направления подготовки «Прикладная математика и информатика» осуществляют научно-исследовательскую деятельность, занимаются практическим применением фундаментальных знаний, полученных в области математических и естественных наук, включая компьютерные технологии. Сферой деятельности выпускников является разработка (на определенном уровне) эффективных методов решения задач естествознания и техники, в том числе с использованием математического и компьютерного моделирования; разработка программно-информационного обеспечения научно- исследовательской, проектнотехнологической деятельности [9,21,22]. Выпускники должны уметь успешно решать задачи профессиональной деятельности, связанные с выполнением фундаментальных и прикладных работ поискового, теоретического и экспериментального характера. Для успешного решения этих задач у студентов должны быть к окончанию вуза сформированы профессиональные компетенции. Формирование профессиональных компетенций, в основном, происходит при изучении специальных естественнонаучных дисциплин, при изучении которых в большинстве рассматриваются методы математического и компьютерного моделирования для решения прикладных задач в области естествознания и техники [13,21-25]. Методы математического и компьютерного моделирования в дальнейшем используются студентами при решении задач учебной, производственной практик и выпускных квалификационных работ [9,14,23,24].

В качестве примера в работе описывается компьютерное моделирование процесса теплообмена при обработке глубоких отверстий расточной борштангой с помощью пакета прикладных программ Flow Vision HPC [26].

Компьютерное моделирование

Известно, что в современном обществе математическое моделирование неразрывно связано с компьютерным моделированием. В настоящее время совершенство вычислительных алгоритмов и вычислительных мощностей современных компьютеров позволяет успешно использовать компьютерное моделирование при решении сложных прикладных задач из различных областей науки и техники с применением пакетов прикладных программ (ППП), таких как Ansys, Flow Vision, Gas Dynamics Tool, Nastran, COSMOS и др. Благодаря тому, что в качестве базовых средств компьютерного моделирования предлагаются пакеты с современным стандартизованным графическим интерфейсом студенты получают навыки работы не только с рассматриваемыми средствами, но и с другими аналогичными. Вследствие стандартизации интерфейса (стандартные меню, контекстные меню, внутренние окна, кнопки, переключатели и др.) студенты тратят значительно меньше времени на освоение пакетов. Главное состоит в том, что графический интерфейс современных ППП закладывает представления о стандартном алгоритме решения прикладных задач. Так практически во всех ППП имеются препроцессор, солвер (расчетный модуль) и постпроцессор [21].

Компьютерное моделирование заключается в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели. Компьютерное моделирование необходимо в случаях, когда натурный эксперимент провести невозможно или он является слишком дорогостоящим. Оно требует от студентов наличия самых разнообразных теоретических знаний и свободное владение информационными технологиями [9,   14-20].    Поэтому компьютерному моделированию в исследовательских целях студенты обучаются в основном на старших курсах при изучении специальных дисциплин. У студентов старших курсов уже имеются необходимые знания основных математических дисциплин: алгебры, математического анализа, теории дифференциальных уравнений, физики. Также студенты в полном объеме владеют численными методами решения линейных и нелинейных дифференциальных уравнений, методами аппроксимации и интерполяции. Для подготовки выпускников, способных решать сложные прикладные задачи профессиональной деятельности, можно выделить два подхода при обучении компьютерному моделированию [9-10, 22]:

Первый подход применяется на начальном этапе обучения. Обычно это происходит при изучении студентами специальных дисциплин на третьем курсе. Обучать практическим навыкам целесообразно на примере простых задач с известным аналитическим решением. Преподаватель формулирует задачу и цели моделирования, проводит анализ объекта исследования, описывает формализацию или переход к математической модели, объясняет, как создать расчетную модель и провести вычислительный эксперимент, а также анализ полученных результатов и проверку корректности полученного решения путем сравнения с аналитическим решениеми.

Во втором подходе используется проектный метод, предполагающий самостоятельную работу студента. Студентам предоставляется возможность самостоятельно изучить предложенный преподавателем объект и происходящие процессы, написать математическую модель, построить геометрию расчетной области и расчетную модель, провести вычислительный эксперимент с использованием пакета прикладных программ, проверить корректность полученного решения. Проектный метод целесообразно использовать также во время прохождения практик, когда студенты уже овладели умениями и навыками работы с пакетом прикладных программ. Полученные результаты проведенных исследований в дальнейшем студенты могут успешно использовать при написания выпускной квалификационной работы.

В качестве примера в работе приводится компьютерное моделирование процесса теплообмена при обработке глубоких отверстий расточной борштангой в ППП Flow Vision HPC [26].

Пример компьютерного моделирования процесса теплообмена в программном комплексе Flow Vision HPC

Кратко опишем принципиальную схему реализации потока смазочноохлаждающей жидкости (СОЖ), используемой для охлаждения зоны резания при растачивании глубоких отверстий. На рисунке 1 представлена модель токарного станка с потоком СОЖ [27]. На рисунке обозначены: 1 - стебель борштанги, 2 -расточная головка, 3 - обрабатываемая деталь, 4 - суппорт, 5 - шпиндельная бабка, 6 – люнеты, 7 – станина. Растачивание производится режущей головкой, закрепленной на конце стебля борштанги. При резании головка формирует цилиндрическую полость в теле детали. Стебель борштанги имеет внутри осевой цилиндрический канал. СОЖ подводится в зону резания по цилиндрическому каналу, образованному внутренней поверхностью растачиваемого отверстия и внешней поверхностью стебля борштанги, а отводится по внутреннему каналу борштанги.

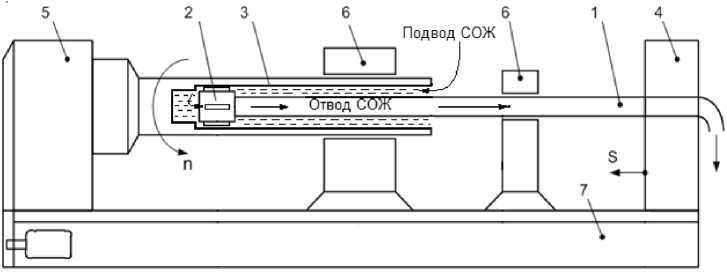
Рис. 1. Модель токарного станка с потоком СОЖ

Компьютерное моделирование в программном комплексе Flow Vision HPC установившегося течения СОЖ в проточной части конструкции выполнено в рамках модели турбулентного течения несжимаемой жидкости с использованием стандартной k-ε модели турбулентности [28].

Трехмерная твердотельная геометрическая модель областей расчета создана в системе автоматизированного проектирования (САПР) SolidWorks. Разработанная геометрическая модель включает в себя три элемента: обрабатываемую деталь, стебель борштанги и расточную головку.

Математическая модель, описывающая установившиеся распределения температуры, скорости и давления, а также турбулентной энергии и диссипации [26] имеет вид:

уравнение энергии

v(pV h ) = V

A

2  №

--+    V h

Cp  P t J

A

J

„ T abs

h = h 0 + J C dT -

T0  р

взаимосвязь между термодинамической энтальпией и температурой

• •    уравнения Навье-Стокса

v(pV ® V) = -VP + v(ц + pt )(vv + (vv)T)+ pg

v(pV)=0

• •    уравнения турбулентности k ²

Pt = C^P —

v(pVk)=v

v(pV£ ) = v

Обозначения:

G = D-ij

д ^

, a xj

Ц + ^

° k J

A A

v k

J

+ ^tG — P£

ц +   1

°£ J

v £

J

+ C 1 jцt^G - C 2 / 1 P ^£—

D

= S..

ij

f      .ь!

v. V + ^

I       ^ t J

δ ij ’

eV-   dVJ

S.. = —i- + —-

J d ij d e-

Параметры:

Ст = 1; ст = 1.3; C.. = 0.09; C = 1.44;   C, = 1.92

о

Граничные условия

В качестве граничного условия на входе во внешний канал борштанги задавалась нормальная составляющая массовой скорости течения СОЖ ( ρV сож ), температура СОЖ ( T in ) и начальная степень турбулизации потока рабочего вещества ( k и ε):

3/2

_v ।      _v      Q         _T I      ( 0.03 • ¹ ) I      ^c m ( k\b )

.

• ^{p V}n\b   ^{p V}_m    S ^; Tb  T in ^; kb               ^{; 0} b

^вх                            2                    0.001

Значение температуры СОЖ на входе равнялось 30 ºС.

На выходе из внутреннего канала стебля борштанги задано условие нулевых возмущений по статическому давлению:

dVn

Pb = °; —

dn b

dT

= 0; — dn b

dk      d e

= 0;—  = 0;—  = 0.

dn b    dn b

На всех стенках конструкции задано условие не протекания с турбулентным пограничным слоем, характеризующимся логарифмическим законом изменения касательной компоненты скорости:

• V . l b = ⁰; ^V t L•а также k|_b , e\_b - через пристеночные функции;

  dT

  
  

  dk

  = 0; —

  
  

  dn _b    dn _b

  На внешних

  
  

  d e = 0; —

  dn _b

  стенках

  
  

  = 0 .

  
  

  температуры T det , в зоне резания -

  
  

  обрабатываемой детали T r .

  
  

  определено значение

  
  

В рассматриваемой задаче имеется зазор между направляющими элементами расточной головки и внутренней поверхностью обрабатываемой детали. Для корректного моделирования течения СОЖ в зазоре применена модель зазора. Стандартная модель зазора, реализованная в Flow Vision, предполагает, что внутри зазора реализуется течение с малыми числами Рейнольдса. При этом предполагается, что внутри зазора существует течение Пуазейля.

Визуализация и анализ результатов вычислительных экспериментов

В ходе исследования процесса теплообмена проведена серия вычисленных экспериментов при различных значениях температуры в зоне резания и температуры подаваемой СОЖ. Получены картины распределения температуры в области зоны резания.

Для численного моделирования были использованы параметры [27], характерные для рассматриваемого процесса.

Параметры борштанги : длина борштанги L = 1.3 м, внутренний радиус борштанги r = 0.03 м, внешний радиус борштанги r = 0.06 м, теплопроводность борштанги 2 X instr = 46 Втм"¹-К " ¹.

Параметры обрабатываемой детали : внутренний радиус обрабатываемой детали r = 0.0855 м, внешний радиус обрабатываемой детали r = 0.1155 м, теплопроводность обрабатываемой детали λ det = 46 Вт·м^-1 ·К^-1.

Параметры расточной головки : длина расточной головки l = 0.24 м, внутренний расточной головки r = 0.03 м, внешний расточной головки r = 0.08 м, длина выступа направляющих элементов n = 0.055 м, длина направляющих элементов равна 0.16 м, длина выступа режущей пластины равна 0.055 м, теплопроводность расточной головки λ instr = 46 Вт·м^-1 ·К^-1.

Параметры смазочно-охлаждающей жидкости ECOCUT HFN 5 LE: плотность СОЖ ρ liq = 830 кг·м^-3, вязкость СОЖ µ liq = 0.00332 кг·м^-1·с^-1, теплопроводность СОЖ λ liq =8.04104 Вт·м^-1·К^-1, теплоемкость СОЖ C _p = 2422 Дж·кг^- 1_·К-1_.

Входные параметры : массовая скорость СОЖ на входе V inl = 415 кг·м^-2·с^-1, скорость вращения обрабатываемой детали ω = 62.8 рад/с, температура подаваемой на входе СОЖ T inl = 30 °С, температура обрабатываемой детали T det = 22 °С, температура рабочего инструмента (борштанги и расточной головки) T instr = 22 °С, температура в зоне резания T r = 800 °С.

Число Рейнольдса (для минимального диаметра потока СОЖ) Re ≈ 20000 .

На рисунке 2 приведены используемые при расчетах способы подвода СОЖ и отвода стружки при растачивании глубоких отверстий, представленные в работе [27]. На рис. 2 а) представлен способ наружного подвода СОЖ и внутреннего отвода стружки. СОЖ подводится по наружному каналу Н между поверхностью инструмента 2 и стенками отверстия в заготовке, а отводится вместе со стружкой через окно С и далее по внутреннему каналу В в инструменте. На рис. 2 б) представлен внутренний способ подвода СОЖ. СОЖ подводится через внутренний канал B в инструменте, через окно С попадает в зону резания Д, а по наружному каналу H отводится между поверхностью инструмента 2 и стенками отверстия в заготовке.

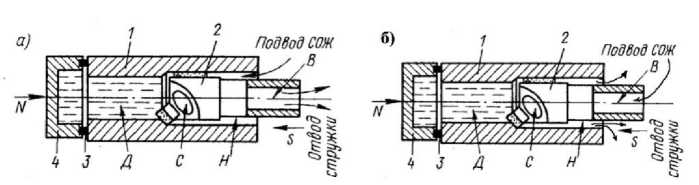
Наружный подвод СОЖ а)

Внутренний подвод СОЖ б)

Рис. 2. Схемы подвода и отвода СОЖ

На рисунках 3 и 4 представлены картины распределения температуры в детали и распределение температуры СОЖ в плоскости XY соответственно.

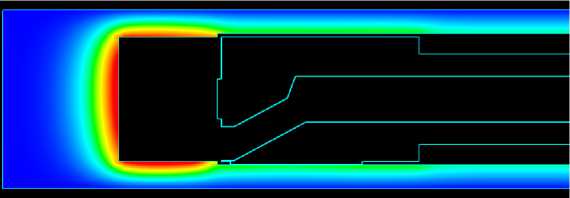
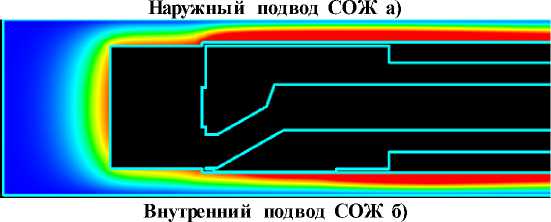
Рис. 3. Распределение температуры в детали в плоскости XY

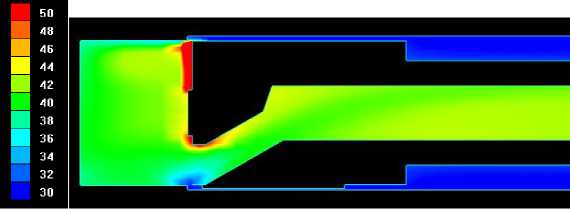
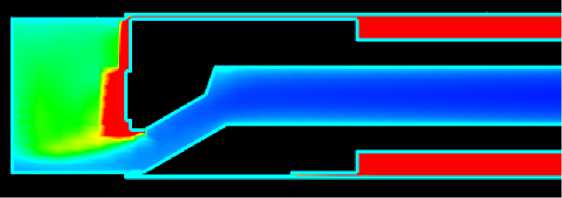
Наружный подвод СОЖ

Внутренний подвод СОЖ б)

Рис. 4. Распределение температуры течения СОЖ в плоскости XY

На рисунках 3 и 4 видно, что при внутреннем подводе СОЖ деталь нагревается сильнее, чем при внешнем подводе.

На рисунке 5 представлена картина распределения температуры в расточной головке в плоскости XY.

Наружный подвод СОЖ

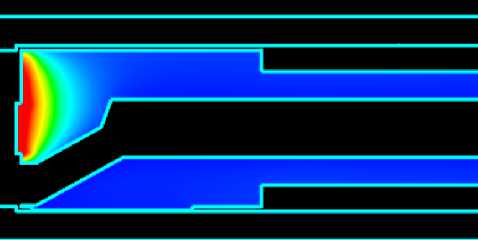
Внутренний подвод СОЖ б)

Рис. 5. Распределение температуры в расточной головке в плоскости XY

На рисунке 6 представлена картина распределения поля температуры в шести секущих плоскостях расточной головки.

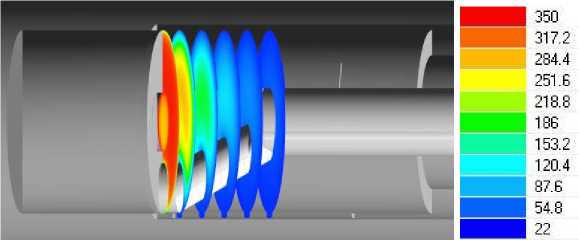
Рис. 6. Картина распределения поля температуры в шести секущих плоскостях расточной головки

При растачивании глубоких отверстий могут быть использованы оба способа обработки, но большее предпочтение следует отдать внешнему подводу СОЖ, так как расточная головка нагревается меньше и отводит тепло лучше.

Анализ результатов вычисленных экспериментов показал, что в данных условиях наиболее резкое изменение температуры происходит в области резания – при удалении от линии соприкосновения резцов расточной головки с обрабатываемой деталью на расстояние ≈ 0,04м температура инструмента падает от 800°С до ≈ 20°С. В остальной области температура незначительно ( ∆T ≈  2-3°С) отличается от начальной температуры инструмента. Этот результат подтверждает пригодность выбранного режима охлаждения для практического применения.

Результаты численного моделирования хорошо согласуются с экспериментальными результатами, представленными в работе [27], следовательно, созданная расчетная модель теплопереноса является адекватной и может быть использована для замены натурных экспериментов при выборе режимов резания в сложных условиях, значительно сокращая время и стоимость выбора технологических процессов.

Заключение

Использование компьютерного моделирования в образовательном процессе позволяет продемонстрировать студентам в наглядном виде протекающие физические процессы, что способствует повышению эффективности усвоения студентами сложного теоретического материала специальных курсов и, как следствие, успешному формированию профессиональных компетенций.

Выпускники, овладевшие методами математического и компьютерного моделирования способны успешно решать задачи профессиональной деятельности, связанные с выполнением фундаментальных и прикладных работ поискового, теоретического и экспериментального характера.