Использование квантовых вычислений при выборе управленческого решения

Особенностью ведения локальных войн на современном этапе является применение средств воздушного и воздушно-космического нападения. Эти средства позволяют достигать целей в вооружённой борьбе с наименьшими затратами и потерями.

Увеличение количества в составе воздушных и воздушно-космических сил ряда стран различных типов и числа беспилотных летательных аппаратов (БЛА) побуждает к поиску принципиально новых форм и способов их боевого применения, а также защиты от их воздействия.

Предполагается внедрение в системы управления БЛА так называемого роевого интеллекта, заменяющего одноканальные системы. Технология интеллектуального управления группой (роем) БЛА должна обеспечить совместные действия отдельных аппаратов за счет обмена информацией и оптимизации выполнения общей задачи на основе коллективного «разума», как это происходит в стаях (коллективах) естественных особей (пчел, птиц и рыб, волков и др.). Предполагается, что с управлением роем БЛА сможет справляться всего один оператор [1].

Внедрение роевого интеллекта в системы управления БЛА может в конечном итоге обесценить дорогостоящие системы противовоздушной обороны. Эти системы просто не будут успевать в реальном масштабе времени отслеживать маневры множественных БЛА, отсекать помехи и противодействовать рою высокоорганизованных БЛА. Появление сверхзвуковых и суборбитальных БЛА делает задачу по их нейтрализации фактически невозможной. Все вышеперечисленное требует от вычислительной системы РЛС увеличения скорости вычислений, уменьшение времени принятия решения при идентификации объекта и принятия решения на его поражение.

Основная задача теории оптимальных решений состоит в представлении количественных данных и рекомендаций для принятия оптимальных решений. Существует несколько моделей принятия управленческих решений:

• 1.    Модель долгосрочного стратегического планирования, которая используется в задачах размещения производства, развитии нефтяной и газовой промышленности.

• 2.    Модель среднесрочного планирования для решения транспортных задач и задач маршрутизации.

• 3.    Модель оперативного управления, которая может применяться в задачах теории расписаний и матричных игр.

Предметом исследований в теории игр являются модели и методы принятия решений в ситуациях, где участвуют несколько сторон. Цели игроков различны и часто противоположны. Здесь стратегией называется набор правил, определяющих поведение стороны, а оптимальной стратегией будет стратегия, при которой достигается максимальный ожидаемый средний выигрыш при многократном повторении ситуации.

По сути, матричные игры – это игры, где две стороны играют в игру с нулевой суммой, имея конечное число «чистых» стратегий: {1, …, m } и {1, …, n } и платежной матрицей (или матрицей выигрышей) ∀ ( ij ) _m×n , определяющей выигрыш первого игрока при выборе стратегий i и j соответственно. В качестве примера одной из таких матричных игр рассмотрим задачу прорыва обороны, в которой один игрок располагает системой противовоздушной обороны (ПВО), а задача второго игрока состоит в прорыве этой обороны с помощью самолетов или беспилотных летательных аппаратов. Тогда элементы матрицы a_ij задают вероятность поражения самолета j системой ПВО i. Платежная матрица задается табл. 1.

Таблица 1

Платежная матрица

i / j	1	2	3		n
1	0.5	0.6	0.8
2	0.9	0.7	0.8
3	0.7	0.5	0.6
m

Для обоих игроков целесообразным является использование чистых стратегий. Отклонение любого из игроков от указанных стратегий может только уменьшить его выигрыш. В этой платежной матрице имеется седловая точка. Седловая точка в матричной игре определяет некоторое положение равновесия, когда ни одному из игроков невыгодно отклоняться от оптимальной стратегии, если противник придерживается своей оптимальной стратегии. В случае существования седловой точки верхняя и нижняя цены игры совпадают и называются ценой игры. Решением игры в чистых стратегиях называется нахождение оптимальных стратегий для каждого из игроков и вычисление цены игры. Соответственно, преимущество в данной игре прорыва обороны получит та сторона, которая сможет быстрее выбрать стратегию противодействия противоборствующей стороне.

Для перебора всех возможных альтернативных стратегий и принятия правильного управленческого решения за ограниченное время требуются большие вычислительные мощности. Так, например, вычислительная способность компьютерных систем современных РЛС типа «Воронеж» составляет порядка 100 млрд операций в секунду. Дальнейшее увеличение быстродействия вычислительной системы РЛС возможно только при наращивании количества процессоров, оперативной памяти, распараллеливанием алгоритмов и вычислений, либо внедрением новых технологий, например на основе квантовых вычислений.

Квантовое вычисление – это контролируемая классическим управляющим компьютером последовательность унитарных операций простого вида (над одним, двумя или тремя кубитами). В конце вычисления состояние квантового процессора измеряется, что и даёт искомый результат вычисления. Содержание понятия « квантовый параллелизм » в вычислении может быть раскрыто так: «Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса преобразуется в классическую путём измерения конечного состояния квантового регистра. Выигрыш в квантовых алгоритмах достигается за счёт того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно» [2]. Таким образом, представляется возможным использовать квантовый параллелизм в задачах селектирования целей и выбора оптимальной стратегии или альтернативы при принятии управленческого решения для поражения множественных целей.

В настоящий момент квантовые вычислительные системы представляют собой технологическую систему, встроенную в классическое окружение, состоящее из управляющего классического компьютера и генератора импульсов, управляющих эволюцией кубитов, а также средствами измерений состояния кубитов. Квантовый компьютер – это вычислительное устройство, которое использует явление квантовой суперпозиции и квантовой запутанности для передачи и обработки данных. Типичная схема квантового компьютера представлена на рис. 1.

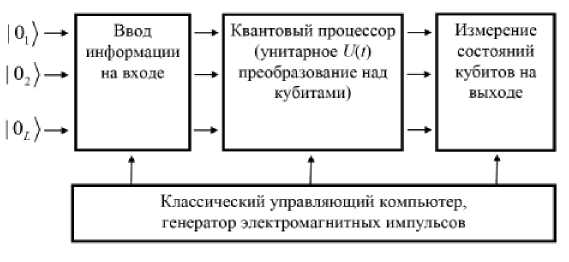
Рис. 1. Схема квантового компьютера

Особенность вычислений на квантовом компьютере состоит в том, что для вычислений используются не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы, использующие квантомеханические эффекты. Квантовый алгоритм представляет собой классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами их надо совершать. Квантовый алгоритм задается либо в виде словесного описания таких команд, либо с помощью их графической записи в виде системы вентилей (quantum gate array). Результат работы квантового алгоритма носит вероятностный характер. За счёт небольшого увеличения количества операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице. К широко известным алгоритмам квантовых вычислений можно отнести следующие алгоритмы:

• 1.    Алгоритм Шора (позволяет раскладывать числа на простые множители за полиномиальное время).

• 2.    Алгоритм Гровера (позволяет решать любые переборные задачи за время, примерно равное квадратному корню из времени, затрачиваемого на классических компьютерах).

• 3.    Алгоритм Дойча - Йожи (позволяет «за одно вычисление» определить, является ли функция двоичной переменной f ( n ) постоянной (f ( n ) = 0, f₂ ( n ) = 1 независимо от n ) или «сбалансированной» ( f₃ (0) = 0, f₃ (1) = 1; f₄ (0) = 1, f₄ (1) = 0).

• 4.    Алгоритм Саймона (решает проблему «черного ящика» экспоненциально быстрее, чем любой классический алгоритм).

Для решения задач перебора альтернатив при принятии управленческого решения хорошо подойдет алгоритм Гровера. Данный алгоритм очень часто используется в задачах перебора при выборе наилучшей альтернативы (шахматы) или в задачах поиска совпадающих строк в базе данных.

Подробное описание формализма квантовых вычислений можно найти, например, в книгах [3; 4].

Рассмотрим подробнее квантовый алгоритм Гровера.

Известно, что состояние одного кубита определяется нормированным на единицу вектором пространства двумерного комплексного пространства С ² :

a |0> + b\ 1), | a|2 + b2 = 1, где через векторы |0) и |1) обозначаются базисные векторы рассматриваемого пространства.

Состояние n -кубитовой квантовой системы есть тензор произведений однокубитовых пространств:

• ( с ² Г n = П n с ² ® С ² ®-® С ² ,

соответствующие векторы имеют вид:

У C ii i„ ) .

^^      i , i 2^,••• i n ^{1 2} — ⁿ'

• i 1 , i 2,--- i n = ⁰

В каждый момент времени состояние меняется под действием некоторого унитарного преобразования. С формальной точки зрения такие преобразования имеют вид U ® I , где U - матрица, действующая на кубиты или кубит, I - единичная матрица, действующая на остальные кубиты. Квантовый алгоритм представляет собой последовательное применение таких преобразований. Входные данные подаются либо в виде начального состояния (вектора) системы, либо в виде выбора применяемых преобразований [5].

Последовательность квантовых операций удобно представлять графически, в виде квантовых схем, пример которой приведен на рис. 2.

Применительно к алгоритму Гровера считаем, что пусть задана булева функция f ( x ) , x е { 0,1 } . Необходимо найти такое значение x , что f ( x ) = 1 . Важно отметить, что для работы алгоритма Гровера необходим так называемый квантовый оракул, переводящий базисное квантовое состояние | x ) в ( - 1 ) ^{f (} x ) | x ) . Тогда квантовую схему, реализующую алгоритм Гровера, можно изобразить в виде схемы - рис. 3 [6].

В силу ограниченности статьи мы не будем объяснять действие его работы - соответствующую информацию можно найти в [3; 4]. Важно отметить, что алгоритм

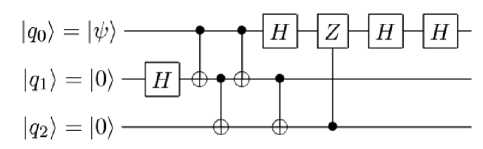
Рис. 2. Пример квантовой схемы. Каждая линия соответствует одному кубиту

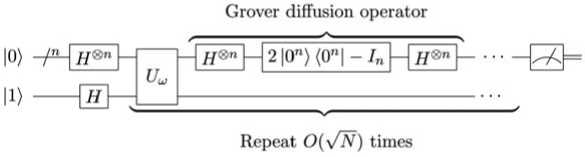
Рис. 3. Квантовая схема алгоритма Гровера

Гровера позволит решить задачу перебора возможных альтернатив или вариантов ре- ( n 1

шения за время OI 22 I, в то время как классический алгоритм в среднем решает за дачу за 2n-1 обращений к функции f (оракулу).

Для использования квантового ресурса в вычислительной системе радиолокационной станции необходимо будет провести следующие манипуляции.

• 1.    Предварительные манипуляции с классическими системами.

• 2.    Приготовление некоторого чистого состояния (обычно это одно из состояний вычислительного базиса).

• 3.    Унитарные преобразования.

• 4.    Измерение в вычислительном базисе.

• 5.    Обработка результатов измерения классическими средствами.

• 6.    Циклическое повторение предыдущих шагов по необходимости.

Предварительные оценки показали, что внедрение квантового компьютера в вычислительную систему радиолокационных станций позволит увеличить ее быстродействие в десятки тысяч раз.

Заключение

В статье предложено использовать элементы квантовых вычислений при разработке новых систем для радиолокационных станций, так как использование квантовых компьютеров позволит увеличить быстродействие вычислительных систем в десятки тысяч раз. Предложено использовать квантовый алгоритм Гровера при создании метода выбора наиболее выгодной альтернативы для образования новых вычислительных систем в радиолокационных станциях.

В то же время имеются до сих пор не решенные проблемы, связанные с квантовыми вычислениями, – это необходимость обеспечения высокой точности измерений и проблема внешних воздействий на квантовую систему, которые могут ее разрушить или внести в неё искажения.