Использование кватернионов при математическом моделировании механизмов с параллельными кинематическими цепями

Одним из путей совершенствования технологического оборудования является использование при его построении нетрадиционных кинематических схем. Часто под такими схемами по нимают схемы механизмов, имеющих параллельные кинематические цепи, связывающие испол нительный орган с основанием [1-3].

Рис. 1

Наиболее известным механизмом с параллельными кинематическими цепями (МПКЦ) является платформа Стюарта - шестикоординатный механизм платформенного типа [4], схема которого показана на рис. 1. В данном механизме платформа соединена с основанием посредством шести штанг длиной L, . Каждая из штанг соединена с платформой сферическим шарниром В,, с основанием - через кардано-вый шарнир А,.

Длины штанг L_t целесообразно принять за обобщенные координаты рассматриваемого механизма, так как они однозначно описывают пространственную ориентацию платформы и удобны с точки зрения управления оборудованием, построенным на базе этого механизма. Однако с точки зрения практического использования более полезны параметры, непосредственно характеризующие положение платформы. Назовем эти параметры выходными координатами механизма. В качестве выходных координат могут выступать координаты сферических шарниров

В,-

Математическая модель механизма должна связывать его обобщенные и выходные коорди наты:

Д² = (^А, - *в, )² + <Уа, -    )² + О_А, - г_В/ )², Z = 1 ...6.                                         (1)

В шесть уравнений (1) входят шесть обобщенных координат и 18 выходных координат. Следовательно, не все выходные координаты являются независимыми. Поэтому уравнения (1) должны быть дополнены 12 уравнениями связи вида [5]

(х_в. — х_в ) +(Ув, ^— Ув^ ⁺(^zb, ^{— z}Bj) ~|В/Ву| ,                                         (2)

где i* j и расстояния между шарнирами В, и В_; известны и постоянны.

Выбором иных выходных координат можно существенно упростить математическую модель. Можно принять в качестве выходных координат механизма три линейные координаты некоторой характерной точки С платформы, назовем ее полюсом, в неподвижной системе координат OXYZ и три угловые координаты, определяющие разворот платформы вокруг полюса из некоторого начального состояния.

В качестве выходных угловых координат могут выступать, например, углы Крылова: угол рыскания ^, угол тангажа 9 , угол крена у [6]. Данные углы позволяют пересчитать координа-

Смирнов В. А., Федоров В.Б.

Использование кватернионов при математическом моделировании механизмов с параллельными...

ты сферических шарниров, заданные в системе координат СХ' Y'Z' , в систему координат OXYZ [5]:

*в, Ув, ^zb, 1

™1

«1 О

А т₂ «2 О

Ц т₃ «з О

хс Ус zc

у* л В/

У'в,

^Z'b, 1

где /] = cos у/ cos у + sin 3 sin у/ sin у ; Z₂ = sin^cos.9; Z₃ =-cos у/ sin у + sin у/ sin 3 cos y.

m_x = -sin у/cos у + sin <9 cos у/sin/; m₂ = cosy/cos.9; m₃ = sin у/sin у + cos у/sin 3 cosy;

И] =cos19siny; n2 = -sin.9 ; и3 = cosi9cos/.

В этом случае уравнения (1) после преобразований примут следующий вид:

А² = (^ХА, - ^с )² + (Уд, - Ус )² + (^ZA, - ^zc )² + ^в, +У в, ⁺²в, + + 2[(с ^Су + S SS ^Sy)x'_B. +S у/ С ^'_в. +(S у/ S ЗСу - С у/ S/)z'_B. + 2 (S ^С ^ Sy - S у/ Су)х'_В/ +С у/ С .9/_в. +(S у/ Sy + С у/ S 3Cy)z'_B. + 2 Сi9Syv'_B. -Si9y'_B;. +С 3Cyz'_B. ^z_c - z_A,), Z = 1 ...6,

№

~*А,) + "Уа,)+

где для сокращения записи введены обозначения: S у/ = sin у/, Су/ = cosy/ и т. д.

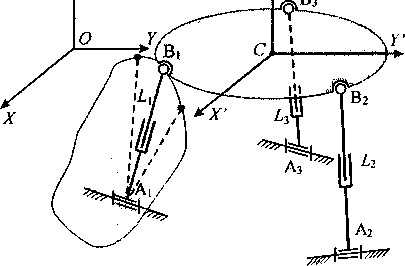
Пусть необходимо составить математическую модель для механизма, показанного на рис. 2. Количество степеней свободы этого механизма Я = 6(8-1)-3-3-5-6 = 3. Следовательно, пространственная ориентация платформы должна описываться тремя обобщенными координатами.

Примем, что обобщенными координатами являются длины штанг L,, выходными будем считать координаты сферических шарниров В, в неподвижной системе координат OXYZ. Запишем уравнения, связывающие обобщенные и выходные координаты:

А² = (^А, - *в, )² + (Уа, - Ув, )² + Оа, - ^В, )², Z = 1 ...3.                                         (4)

В уравнения (4) входят 9 координат сферических шарниров, следовательно эти уравнения должны быть дополнены 6 уравнениями связи. Однако для рассматриваемого механизма можно записать только три уравнения, аналогичные (2):

Ав, — хВ2) +(Ув, — Ув2) + AB] — гв2) = |В1Вг| >

Ав2 - ^в3 )2 + (Ув2 - Ув3 )2 + (гв2 - ZB3 )2 = |В2В3 Г ;                                           (5)

(х_В] -Х_Вз)² +(у_В] -Ув₃) + Abj ^-ZB₃)² = |^В1^Вз| ■

Остальные уравнения связи должны быть записаны из каких-то иных условий, например, учитывающих, что точки В, - центры соответствующих шарниров, лежат в заданных плоскостях.

На рис. 2 показана плоскость, в которой лежит 7                  .7- точка В,. Данная плоскость проходит через штангу Д перпендикулярно прямой, являющейся осью вращения шарнира Aj. Если ось вращения шарнира Aj задана уравнением

^-^а, ₌ У~У_{А1 =} ^-^а,

А, ^А!      «А1 ’ где ZA], mkx, n^x - направляющие косинусы в системе координат OXYZ, то уравнение плоскости, перпендикулярной этой прямой и проходящей через точку В], будет иметь вид [8]

А, (^-^В1) + тА,(У-Ув1) + ИА1(2-гВ1) = °-

Так как эта плоскость проходит через точку пересечения штанги 1^ с осью вращения шар нира А! (точку А!), то можно записать дополнительное уравнение связи

Расчет и конструирование

к_х 0_А1 " ^хв,) + ^тА, (Уа, ~ Ув,) + «_А1 (г_А1 - 2_В1) = 0.

Аналогично для остальных штанг:

^za₂ Оа₂ - ^в₂) + '«А, (Уа₂ ~ Ув₂) + «а₂ (^а₂ - ^в₂) = 0;

^ZA₃ (^ХА₃ - ^Вз ) ^{+ W}A₃ <Уа₃ ~ Ув₃ ) ⁺ «Аз (^ZA₃ ~ ^В₃ ) = °'

Оси вращения цилиндрических шарниров обычно лежат в плоскостях, параллельных плоскости ОХУ . В этом случае и_А) = п_Кг = л_Аз = 0 и дополнительные уравнения связи несколько упростятся:

к_х (^ха, " ^в.) + ^т^ (Уа, - Ув,) = о;

к₂ (^ха₂ - *в₂) + ^wa₂ (Уа₂ - Ув₂) = о;                                                      (6)

к₃ 0% ~ *в₃) + ^Аз <Уа₃ - Ув₃) = ⁰ •

Совместное решение девяти уравнений (4)—(6) позволит определить выходные координаты по известным обобщенным координатам, т. е. решить прямую задачу о положениях.

При решении обратной задачи о положениях необходимо задать три выходные координаты и с использованием уравнений (4)-(6) определить обобщенные координаты - длины штанг L,.

Если при функционировании механизма представляет интерес пространственное положение его платформы, то в качестве выходных координат целесообразно использовать координаты полюса С в системе координат OXYZ и три угловые координаты, характеризующие поворот платформы вокруг полюса - углы Крылова. В этом случае для решения задач о положениях потребуется совместно решать шесть уравнений - по числу выходных координат механизма:

к¹ = (^А, - ^'в, Чу'в, Ч^'в, ~^хс )² + (уА, - «^'в, -«ЧУв, -т^к_х -Ус У +

+ (^ - «1^_В1 "«гУв, -«з^'в, -z_c У;

• -^2 ⁼ (^ХА₂ ~Л^Х*В₂ ~кУв₂ “^Z3^Z'b₂ ~^Хс) ⁺(Уа₂ ~^т1^Х'в₂ -^т2У в₂^-тз²'в_г ^-Ус) ⁺

+ (zA2 -п1х’в2 -и2Ув2 -w3z'b2 -zc)2;

к² = (^ха₃ -^^Вз-^У'вз^з^Вз-^с)² +(Уа₃ -^’вз-^Увз-^з^Вз-Ус)² +             ^

+ (2д₃ -И,*^ -И₂У*Вз -^И3²'в₃-2сУ;

• к, (^ха, ~ А^*_В| ЧУв, Ч^'в, ~^хс)+ "% (уа, - «^Ч -«ЧУв_х -«Vb, -Ус)= °;

к₂ (^ха₂ - А^х'в₂ ЛУв, 4^z'b₂ ~^хс )+ т_Кг (у_А2 - Щ,У_В2 -/и₂Ув₂ -«^'b₂ "Ус )=°;

кз (^ХА₃ - ккз -^У'вз ^З^В, ~^ХС )+ ^тА₃ (Уа₃ - ^^'вз -^т1Ув₃ "«^В, ~У_С)=^-

Уравнения (7) получены из (4) и (6) с использованием (3). Уравнения (5) исключены из рассмотрения, так как при подстановке в них координат сферических шарниров, рассчитанных с использованием (3), они превращаются в тождества.

Из шести выходных координат только три являются независимыми. Принять, какие из выходных координат использовать в качестве независимых, т. е. для каких координат задавать значения при решении обратной задачи о положениях, зачастую можно только по результатам численного решения прямой задачи для различных значений обобщенных координат.

Покажем, как могут быть решены прямая и обратная задачи о положениях для рассматриваемого механизма с использованием кватернионов.

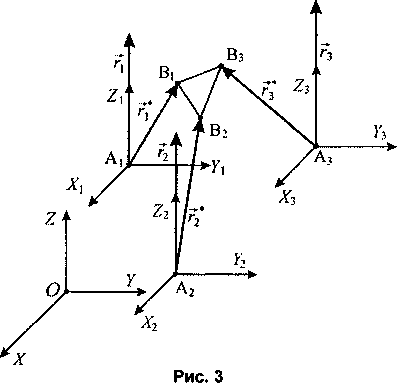
Введем в рассмотрение систему координат A_xX_xY_xZ_x , оси которой сонаправлены соответствующим осям системы координат OXYZ, и вектор г_х, начало которого совпадает с точкой А, (рис. 3), а координаты равны г_хх = 0, г_ху = 0, r_X7=L_x. Очевидно, что вектор г_х соответствует вертикальному положению штанги L_x . Положению этой штанги при работе механизма соответствует вектор г_х . С использованием математического аппарата кватернионов [7] переход от вектора г_х к вектору г* можно записать как

П*=А1о^оЛ1,

Смирнов В.А., Федоров В.Б.                 Использование кватернионов при математическом

______________________________________________ моделировании механизмов с параллельными... где Aj - нормированный кватернион, заданный в системе координат A_xX_xY_xZ_x ; Л] - кватернион, сопряженный с Л!; ° - символ операции умножения кватернионов.

Координаты точки В] конца вектора г_х определяются следующим образом:

*В1

/в1?

= A,o^oA₁₊ у_А)

/А1 7

Аналогично могут быть получены координаты точек В2 и В3.

Кватернион Л как гиперкомплексное число записывается в следующей форме:

Л — Ху + i_xX^ + /2^ "*" ^3^3 ’                 СО

где Х₃ - действительные числа; i₃ - мнимые

единицы. Для нормированного кватерниона ^+^2+^+^=1.            (10)

Кватернион Л, сопряженный с Л, записывается как

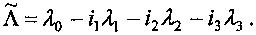
(И)

Применительно к задаче описания вращения твердого тела, имеющего закрепленную точку, мнимые единицы ij трактуются как орты некоторой прямоугольной системы координат. При таком подходе параметры Х} определяют направление оси поворота твердого тела в системе координат, задаваемой ортами ; параметр Ху характеризует угол <9* поворота тела вокруг этой оси: Ху = cos.9*/2.

Примем, что для кватерниона Л, орты / сонаправлены осям системы координат А_хX_xY_xZ_x. С учетом (9) и (11) и свойств кватернионов [7] распишем преобразование (8):

^Bj ⁼ (Ли ⁺ Ai ~Ai ^— Ai) ‘4% "*"2(AiAi ~ Ал Ли)" Чу ⁺ 2(AiAi ⁺ А1А1)"4z ⁺ -^А] ’ УВ] ⁼ 2(AiAi ⁺ AiAi)'4x + (Ai ⁺ ^i ”'^i 1 ~ Asi)'^rir ⁺ 2(Я₂₁Я₃₁ - Х_охХ_хх) • r_lz + у_А]; z_B1 = 2(Л_ПЯ₃₁ -ЛнА1)^-Ч.у + 2(Х₂₁Х_зх + АлА1)'Чу + (Ло1 + Ai ~Х_хх - Ai)‘4z + z_A).

Так как г_1У = г_1У = 0, r_xz = Д и Х^ = 0, полученные выражения существенно упрощаются:

^Хв₁ ~2AiAiA +x_Ai; у_В) -у_А] 2X_oxX_xlL_x; z_Bi -(2Ху_Х 1)Д + z_A].

Условие Хз_Х = 0 следует из того, что любое положение штанги можно рассматривать как поворот в шарнире А, из исходного вертикального положения на угол 3* вокруг оси, лежащей в плоскости X_xA_xY_x . Причем ориентация этой оси в плоскости задана, что устанавливает связь между компонентами кватерниона: Ai = k_xX_xx, k_x = m_AJl_Ax . Выражение для координаты z_B] записано с использованием условия (10) нормирования кватерниона.

Для определения параметров кватернионов запишем с использованием (12) уравнения вида (^в, ~^в_у)² +Ов, -Ув₇)² + (^в, ~^гв,)² = |^ву^в/|^{2 :}

(2АА2А2А + ^ха₂ ~2k_xXy_XX_vxL_x -х_А|) + (2X_oxX_xxL_x -у_А(-2Х₀₂Х_х2£₂ + у_А^ ⁺

₊ {2^₂ -1К ₊z_Ai -[2^ -1]Д -zj² -|В₂В,|²;

Расчет и конструирование

Р^Аз^-^ 2^₁Я₀₁Я_1]2₁ x_AJ +12^^^-Ул,"24ti + Уа₃ / +           ^

⁺ ([24 ^_ Фз ^{+ z}a₃ “ |?4 ^_    ~ ^za, ) ~ М1 >

(2^442 ^{+ х}а₂ — 2к₃Лоз Аз^з — ^ха₃ ) + (244-^3 ~ Та₃ —2444 ⁺ Та₂) ⁺

+ ^2^02 - 1^ + ZA2 “ ^4 - ^ - ZA3 ) ~ |В2В3| , где расстояния |ВуВ,| между шарнирами известны и при работе механизма не меняется.

Для определения величин Лщ, Лц, Л02, Л,2, Лу3, ^3 уравнения (13) должны быть дополнены уравнениями

4 + 4(i+^²)=i_; 4+4d+4²)=i; 4 + 4(i+^)=h                    (14)

следующими из условия (10) нормирования кватернионов. Из уравнений (14) можно записать:

1+V ’

1-4 .

1+£2 ’

1-4

что позволит уменьшить количество параметров кватернионов в (13) до трех:

2^₉Лп₇Л----4,+х_А +2^,Л_П1Л--- ^-L -х

+ 2Л01

1 + fc 1

²^²р + к^{2 2 А2 1ЧП}р + Л1

24 4 , 2 ^2 ⁺ У А р + к₃

⁺ ([24 — 1]^2 + ^Z.

2^4                      -хА

3^1 + к32 3 Аз ^р + к?^ А'

+ -2^0!

1 + ^2Z*

24 J 1 ,2 4⁺Та У 1 + «3

+ ([з Луз  l]z,₃ + z_k

244 ■у । ₊ ^2 4 ^{+ х}д₂ 244

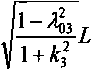
З-^А.

+ 2Лщ3

о А Уд 1 + £₃²

[24 1^3 ZA3) - |®2®з| ■

Знаки перед радикалами в (15) расставлены из анализа знаков координат сферических шарниров, получаемых с использованием преобразования (8).

Решение уравнений (15) позволяет при заданных обобщенных координатах L, определить параметры кватернионов и, далее, с помощью зависимостей (12) и аналогичных, записанных для других сферических шарниров, определить координаты этих шарниров. Тем самым решается прямая задача о положениях. Использование кватернионов позволило снизить количество совместно решаемых уравнений с девяти до трех. Численное решение уравнений (15) авторами выполнялось с использованием пакета MathCad.

Технологическое оборудование, построенное с использованием рассматриваемого механизма с параллельными кинематическими цепями, можно использовать для перемещения заготовки, установленной на его платформе, в вертикальной плоскости с поворотом ее относительно двух горизонтальных осей. Требуемые для этого перемещения платформы можно описать с помощью трех выходных координат: координаты z_c полюса и двух углов Крылова (тангажа S крена у ).

Смирнов В.А., Федоров В.Б.                 Использование кватернионов при математическом

______________________________________________ моделировании механизмов с параллельными... Поэтому при решении обратной задачи целесообразно выбрать в качестве трех известных выходных координат механизма величины Z_c, S и у .

Составим уравнения, позволяющие решить обратную задачу при принятых выходных координатах. С использованием третьего уравнения из (12) и аналогичных ему можно записать следующие выражения:

(2Лл — 1)7. + z_A) = n^ _Bj +и₂у _B] +n₃z _В) +z_c ;

(2<1q₂ ^—l)-^ ^{+ z}a₂ ⁿi^x в₂ ^гУ в₂^+из² в₂ *^zc ’                                             О 6)

(2^3 -1)^3 + ^ZA₃ = ”1^'в₃^+й2Ув₃^+И3*В₃ ^+ZC •

Направляющие косинусы, входящие в (16), определяются только углами & и у .

Из выражений (16) можно выразить длины штанг L,: п_хх'_йлп₂у'_ълп₃г'_йлг_с-г_к

Li  ---- ¹-----±2—Г------- ’ ^z "^L-³-                                       <¹⁷⁾

Подстановка (17) в (15) позволяет получить систему трех нелинейных уравнений, которая связывает три принятых независимых выходных координаты механизма с тремя неизвестными параметрами кватернионов Я^ , Л₀₂, ^. Численное решение этой системы позволит, с последующим использованием (17), определить обобщенные координаты L, при заданных выходных координатах Z_c, &  и у, т. е. решить для рассматриваемого механизма обратную задачу о положениях. Как и в случае прямой задачи, при использовании кватернионов количество совместно решаемых уравнений снижено до трех.

Уравнения, полученные для решения задач о положениях, служат основой для численного решения задач о скоростях и ускорениях. Следовательно, гиперкомплексные числа кватернионы могут быть успешно использованы при моделировании механизмов с параллельными кинематическими цепями путем решения прямой и обратной задач кинематики.