Использование лидарных измерений для краткосрочного прогноза устойчивости метеоситуации

В настоящее время растет потребность в краткосрочном прогнозе метеорологической ситуации, из-за роста ее резких непрогнозируемых изменений. Эффективным средством такого прогноза может оказаться анализ устойчивости структуры оптических неоднородностей стратифицированной атмосферы замутненного приземного слоя. Это связано с разной пространственно-временной инерционностью процессов формирования структуры оптических неоднородностей и метеорологических (термодинамических) процессов в атмосфере, что создает благоприятную почву для поиска соответствующих предикторов.

Рассмотрение различных методов обработки полученной информации, применяемых в лазерном зондировании, метеорологии, радиолокации, квантовой спектроскопии, позволило выявить дополнительные возможности анализа сигналов сложной формы, отражающих процессы самоорганизации сложных систем, включая земную атмосферу.

Они основаны на следующих составляющих:

• -    одноканальной привязке корреляционного анализа, путем выделения локальных максимумов и минимумов сигнала и приведении их к нормированной амплитуде.

• -    нелинейной фильтрации выявленных локальных экстремумов сигнала, позволяющей, на основе введенного критерия, выделить изменения обусловленные средой, на фоне изменений вызванных квантовой природой самого сигнала и внешней засветкой

• -    разделении выявленной структуры сигнала на две, локальных максимумов и локальных минимумов (‘плюс’ и ‘минус’ структуры), позволяющем раздельно исследовать поведение соответствующих образований среды (структур локальных помутнений и просветлений)

• -    получении статистически обобщенных характеристик выявленных структур, их динамики и связности, на основе усреднения полученных данных.

Метод предполагает регистрацию спадающего в среднем по экспоненте сигнала рассеяния, когда флуктуации сигнала подобны дробовым шумам, растут со средним уровнем сигнала.

В качестве примера, была проведена обработка лидарных сигналов обратного рассеяния полученных в режиме счета фотонов с накоплением. Для этого осуществлялась следующая последовательность действий:

• 1)    Строилось распределение числа фотоотсчетов n_c(t, T) в каналах регистрации, причем по оси ординат откладывалось значение, пропорциональное числу отсчетов в каждом канале.

• 2)    Значение n_с в каждом канале относилось к центру соответствующего временного интервала.

• 3)    Полученное распределение n_c°(t, T) сглаживалось в предположении, что число отсчетов меняется при переходе от локального максимума (минимума) сигнала к локальному минимуму (максимуму) по линейному закону.

• 4)    Сглаженное распределение n_c°(t, T) разбивалось на участки, границами которых были два соседних локальных максимума (n_Сmax1, n_Cmax2) или минимума сигнала (n_Cmin1, n_Cт1п2).

• 5)    Значение минимума n_Cmin между n_Сmax1 и n_Сmах2 принималось за действительный локальный минимум сигнала при выполнении условия:

(п Сmах1,2 - n Cmin )> Δn c = (0.3 – 0.4) n Cmin (1)

• 6)    В противном случае локальный минимум исключался из рассмотрения и проводилось повторное сглаживание по п. 3.

• 7)    Для каждого выделенного участка распределения n_c(t, T), ограниченного соседними локальными максимумами сигнала, проводилось преобразование по методу одноканальной привязки, согласно условиям:

n k (t, T) = 1 при n c (t, T)>k, (2)

nk(t, T) = 0 при nc(t, T)≤ k, где nc — число фотоотсчетов в канале, отнесенное к центру временного интервала t, t+T; T — длительность временного интервала накопления сигнала в каждом канале (0,8 мкс); k — уровень привязки, равный средней скорости счета на выделенном участке.

• 8)    Для участков ограниченных соседними локальными минимумами сигнала использовались аналогичные преобразования сигнала:

n k (t, T ) = - 1 при n c (t, T) ≤ k, (3)

n k (t, T) = 0 при n c (t, T) > k.

• 9)    По полученным нормированным квантованным сигналам (±1) судили об интервалах между максимумами m₁минимумами m₂и между максимумами и минимумами m_3,в предположении совпадения экстремума с центром элемента разрешения.

3.    Результаты

Условие (1) обеспечивало выделение неоднородностей сигнала, имеющих контрастность 30 - 40% относительно минимального на участке уровня n_Cmln. Введение этого условия связано с необходимостью выделить скачок сигнала, обусловленный средой, даже на фоне сигнала, определенного с максимальной погрешностью (10 - 20%).

Раздельная одноканальная привязка по локальным максимумам и минимумам сигнала позволяла получить неискаженную информацию о спектрах интервалов «положительной» и «отрицательной» структур. Пространственная дискретизация по трассе с шагом Δ обеспечивала регистрацию структур с характерным размером между центрами соседних элементов структуры m = 240-2040 м при шаге Δ = 120 м и числе элементов 114

разрешения KA = 2, 3, ..., 17. Такая дискретизация приводила к росту фактической пороговой контрастности дальнего из двух взятых экстремумов пропорционально коэффициенту р = (1 - ехр (-2а ср Ш^А)), где а_ср - средний коэффициент ослабления среды . Это позволяло повысить надежность регистрации экстремумов (обусловленных именно неоднородностью среды) с ростом расстояния между ними.

В соответствии с принятыми допущениями устанавливался плавающий порог, позволяющий выделить локальные изменения сигнала несущие информацию непосредственно о зондируемой среде, независимо от величины регистрируемого сигнала, когда его уровень превышает уровень фона в требуемое число раз. Если соответствующий локальный максимум сигнала превышал установленный порог, он считался обусловленным зондируемой средой. В противном случае локальный максимум сигнала исключался из рассмотрения, а из пары ближайших локальных минимумов исключался меньший.

Информацию о периодичности структуры неоднородностей зондируемой среды дает распределение выделенных временных интервалов N(m), где N - число интервалов между локальными максимумами (минимумами) протяженностью m шагов дискретизации сигнала. Для формирования обобщенной структуры неоднородностей среды по выделенным экстремумам сигнала дополнительно использовалась определенная последовательность действий статистической обработки.

Такой подход можно назвать структурным анализом статистически обобщенного сигнала. Основной характеристикой такого анализа является распределение числа соответствующих временных интервалов между локальными экстремумами сигнала, в зависимости от их протяженности. Можно говорить о спектре таких интервалов, как основной характеристике. Здесь локальный экстремум – точка смены знака производной сигнала, т.е. отдельное отклонение сигнала на временном интервале малой длительности, относительно общего подъема или спада сигнала. В результате получают последовательность дискретных отсчетов обработанного сигнала отражающего только характерную регулярность структуры исходного сигнала.

Эффективность такого подхода проверялась на примере обработки результатов лазерного зондирования атмосферы [1] и численным моделированием [2].

Удалось выявить достаточно устойчивые и регулярные турбулентные структуры в условиях относительно устойчивой атмосферы приземного слоя, их трансформацию при изменении метеоситуации [3]. В качестве обобщенных характеристик выявленных структур выбраны математические ожидания величины интервалов между локальными максимумами ( М₁ ), локальными минимумами ( М₂ ), максимумами и минимумами ( М₃ ) и их дисперсии ( D₁, D₂, D₃ ). Оказалось, что характерный размер структур M_1,2 лежит в диапазоне длин 375 - 520 м и соответствует данным радиолокационных измерений в аналогичных условиях (рис.1, где по вертикали - величина интервала в элементах разрешения Δ = 120 м, по горизонтали – номер района зондирования).

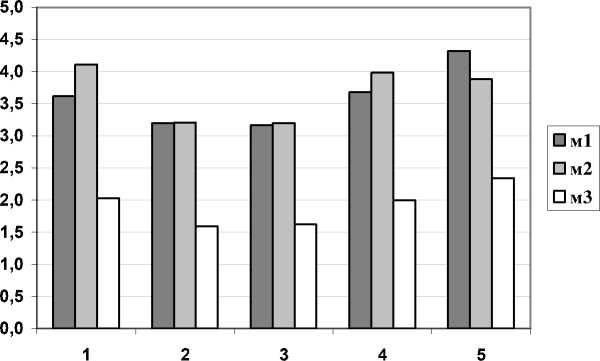
Рис. 1 . Результаты определения интервала между элементами обобщенной структуры разного типа ( M₁, M₂, M₃ ) для оптических неоднородностей атмосферы пяти выбранных районов зондирования.

Соответствующие значения дисперсий ( D₁, D₂, D₃ ) приведены на рис. 2. Здесь доверительный интервал M_1,2 для трех районов зондирования (2,3,4) и М_1,3 четвертого района (1) не превосходит

Доклады независимых авторов 2006 выпуск №6 размера элемента разрешения Δ и несколько больше в остальных случаях.

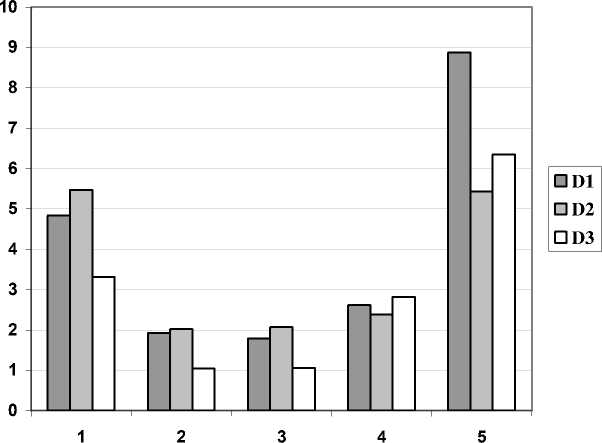
Рис. 2. Результаты определения дисперсии интервала между элементами обобщенной структуры разного типа ( D₁, D₂, D₃ ) для оптических неоднородностей атмосферы пяти выбранных районов зондирования.

Среднеквадратичное отклонение S_1,2 = (D_1,2)^1/2 для районов 2, 3, 4 не превосходит величины M_1,2/2. Причем в районах 2, 3 структуру можно считать гармонизированной и связной (‘плюс’ и ‘минус’ структуры неразличимы), что может быть косвенным признаком устойчивости соответствующих структур и метеорологической (термодинамической) ситуации в целом. Этого нельзя сказать о структурах неоднородностей в районах 1, 5, где доверительный интервал среднеквадратичного отклонения велик ( ε_pmax = 3,24 Δ ). Здесь динамичность структуры не позволила выявить ее особенности с помощью используемой аппаратуры.

Следующим этапом работы был поиск связи характеристик обнаруженных структур атмосферных образований с устойчивостью метеоситуации.

В качестве такого критерия бралось обобщенное значение разности приведенных чисел Ричардсона ΔRiΣ, которое рассчитывалось по следующей методике, на основе стандартных данных Гидрометеоцентра в районе зондирования:

• 1)    Определялось число Ричардсона: Ri = (g/T₀)(Y_a - Y)/e 2 (где g -ускорение свободного падения, Т о - абсолютная температура у поверхности, Y_a = 1^o/100 м, Y =AT₀/Ah, e=Av/Ah) для слоев атмосферы от поверхности до высоты измерений h = 100, 200, 300, 400, 500, 600, 900, 1000 м.

• 2)    Полученные значения Ri приводились к интервалу h = 1 м в допущении линейного измерения Ri с высотой:

Rih(n) = Ri/h.(4)

• 3)    Для каждой высоты измерений находилась разность приведенных чисел Ричардсона для времен 21 ч (1) и 3 ч (2) в пределах которых проводились измерения :

ΔRih(n) = Rih(n) (t2)- Rih(n) (t1)(5)

В качестве критерия устойчивости в определенном районе зондирования бралась обобщенная разность :

n

δRiΣ = Σ δRih(n)/n(6)

n=i

Для районов 1—5 соответственно получены следующие значения критерия термодинамической устойчивости стратификации ARi_s : 0,813; 0,020; 0,114; 0,004; 0,026.

Связь между характеристиками выявленных структур атмосферных образований М, D и критерием устойчивости стратификации ARi_s оценивалась по коэффициенту линейной корреляции К с доверительной вероятностью р . Оказалось, что по результатам для всех пяти районов связь существенна для следующих характеристик структур: М 2 , М 1 - М 2 , М 2 - М 3 , M 1 /M 2 , D 2 , D 2 - D₃ (K > 0,5, р > 0,8 ) . Особенно высокие значения К и р получены для связи между М 2 - М 3 и ARi_s ( K =0,84, p = 0,98).

Отметим, что метеопараметры определялись на метеостанции не далее ~10 км от зоны зондирования, при временном интервале между метеорологическими    измерениями,    максимально превышающем время, необходимое для зондирования, на три часа. Для конкретизации характера связи М2 - М3 и ARis получены уравнения регрессии типа а + Ьх :

М 2 - М 3 = 0,656 ARi s + 1,604,                     (7 )

ΔRi Σ = l,513 (M 2 - M 3 ) - 2,426.                        (8)

Различие коэффициентов а и b , полученное при переходе от уравнения регрессии М2 - М3 по ΔRi_Σ к уравнению ΔRi_Σ по М₂ - М₃ и противоположном переходе (ΔRi_Σ(M₂ - М₃) → (М₂ -M₃)/ΔRi_Σ) , не превышает 3,5%.

Для уравнения (7) среднеквадратичные ошибки определения коэффициента регрессии b и коэффициента а равны соответственно 12 и 2,5%. Для уравнения (8) они меньше и равны соответственно 5 и 0,8%. Это обусловлено большей статистической обеспеченностью определения параметра М₂ - М₃.

В предположении отклонений фактических значений от линии регрессии, следующих нормальному распределению, гипотеза об отсутствии линейной зависимости упомянутых переменных имеет вероятность Р ~ 10^-3. Следовательно, можно говорить о линейной, фактически функциональной связи (М₂ - М₃) и ΔRi_Σ. Эта связь позволяет по изменению величины М₂ - М₃ , измеренной с интервалом времени в несколько часов, прогнозировать изменение устойчивости стратификации пограничного слоя атмосферы, а косвенно - и устойчивости метеоситуации.

Дальнейший поиск связи между характеристиками выявленных структур и метеопараметрами анализируемого слоя атмосферы ( h = 0 - 1 км) показал, что все параметры структуры (М, D) сильно связаны с разностью средних значений относительной влажности, приведенных к слою в 1 м и, также полученных по данным измерений в 21 ч и 3 ч: Δf ° = Δf₁ - Δf₂ , где n

δ f 1,2 = Σ δ f ⁰ 1,2 /n, δ f ⁰ 1,2 = (f h1 - f h2 )/Δh.           (9)

n=1

В этом случае коэффициенты корреляции (несмещенная оценка) и вероятности их значимости не ниже 0,6 и 0,8 соответственно. Для наиболее существенной связи S₃ и Δf ⁰ получены уравнения регрессии:

S 3 = 0.560Δf ⁰ + 1,026,                              (10)

Δf 0 = 1 ,758S3 – 1,784.                             (11)

Переход от уравнения (11) к уравнению (10) дает максимальное различие коэффициентов а и b соответственно 1 и 3 %. Среднеквадратичная ошибка определения коэффициентов а и b не превышает соответственно 8 и 9%. Гипотеза об отсутствии линейной зависимости S₃ и Δf ⁰ имеет вероятность Р ≤ -10^-3.

Дополнительно, для районов с температурной инверсией (районы 1, 2, 3, 5), обнаружена связь параметров нестабильности структуры атмосферных образований S 1 - S 3 с параметрами, характеризующими изменчивость инверсионного слоя между измерениями ( AvAh/AT, где Av — изменение скорости ветра, Ah — изменение мощности слоя, AT — изменение скачка температуры в слое). Получены следующие уравнения регрессии:

S 1 - S 3 = 0.01ΔvΔh/ΔT + 0,34, (12)

ΔvΔh/ΔT = 99.56(S 1 - S 3 ) - 31,95. (13)

Переход от уравнения (13) к (12) дает различие в коэффициентах а, b соответственно 0,5 и 7%. Среднеквадратичная ошибка определения этих коэффициентов 2 и 4%. Гипотеза об отсутствии линейной зависимости имеет вероятность P ~ 10^-3. Однако переход от уравнения (12) к уравнению (13) дает различие в коэффициентах а и b соответственно 43 и 50%, а среднеквадратичные ошибки их определения 17 и 48% при вероятности отсутствия линейной зависимости Р = 8*10^-2. Следовательно, эта связь носит более статистический характер, чем предшествующие, и, возможно нелинейна. Для уточнения ее вида необходимы дополнительные специальные измерения. Тем не менее полученные результаты позволяют говорить о существенной связи комплекса параметров структур атмосферных образований с устойчивостью комплекса метеопараметров, характеризующих влажность атмосферы и приподнятую инверсию.

Это открывает дополнительные возможности для прогноза с использованием метода обнаружения оптических аномалий [4], появление которых может быть обусловлено мощными локальными нарушения термодинамической устойчивости атмосферы, не связанными с повседневной метеоситуацией.

Метод основан на разрешении противоречия между необходимостью сгладить изменения сигнала, обусловленные структурой его неоднородностей, фоновыми шумами, и необходимостью усилить изменения сигнала вызванные присутствием в среде аномальной (не свойственной ее равновесному состоянию) неоднородности.

Фактически предлагается обрабатывать сигнал путем нелинейной фильтрации его структуры.

Алгоритм такой фильтрации предполагает следующие этапы:

• 1)    Деление пополам временных интервалов регистрации импульсного сигнала рассеяния, задаваемого с определенным шагом дискретизации от момента излучения до текущего момента времени

и от текущего момента времени до момента его спада к уровню минимальной требуемой точности измерений.

• 2)    Вычисление логарифма отношения сигналов для таких интервалов, при нарастании интервалов регистрации сигнала в процессе его распространения, с шагом равным удвоенному шагу дискретизации принимаемого сигнала.

• 3)    Умножение полученного ряда дискретных значений сигнала на отношение полного числа отсчетов сигнала от среды к числу отсчетов на взятом интервале.

• 4)    Выделение неоднородности среды, как аномалии в поведении сигнала, путем соотнесения провалов во временном ходе отфильтрованного сигнала с границами такой аномалии, когда чем уже и глубже такой провал, тем контрастней аномалия.

В общем случае алгоритм выявления аномалии полученной структуры сводится к выражению:

T4        T2

S tn = ln

( ∫ S(t)dt/ ∫ S(t)dt ) /t n/2 T3        T1

где Т 1 = t o , Т 2 = t n , Т 3 = t n + t 1 , Т 4 = 2 t n + t 0 (при n = 2,3 ,…, n x ); Т 1 = t _n, Т₂ = t _o, Т₃ = 2 t* n + t ₀, Т₄ = t* n+ t ₁ (при n = n_x + 1, n_x + 2,…, n_MAX ); когда t ₁ = Δ t (шаг дискретизации сигнала), n_x определяется из условия |( S_{tn –} S_t*n )| = min.

Численное моделирование и сравнение этого метода с линейной и медианной фильтрацией показало его высокую эффективность в выявлении резких перепадов сигнала на фоне близкой по мощности регулярной структуры неоднородностей типа выявленной в предшествующих измерениях (рис. 3, где, LINF -линейный фильтр, MEDF - медианный фильтр, GRAN -специальная фильтрация, DISP1, DISP2 - дисперсии до и после введенного перепада сигнала принятые как мера аномальности, SIG – сигнал на выходе фильтра при отношении между максимальным значением сигнала, аномальным перепадом и шумом - 10:1:10).

Аномалии подобные модельным широко встречаются в реальности и могут быть обусловлены как резкими атмосферными процессами стихийно-катастрофического характера, так и техногенными катастрофами вне зоны измерений, когда жизненной потребностью становиться возможность предсказать пространственную траекторию движения такой аномалии. Дополнительные исследования в этом направлении могут дать богатый материал для формирования набора предикторов для таких ситуаций.

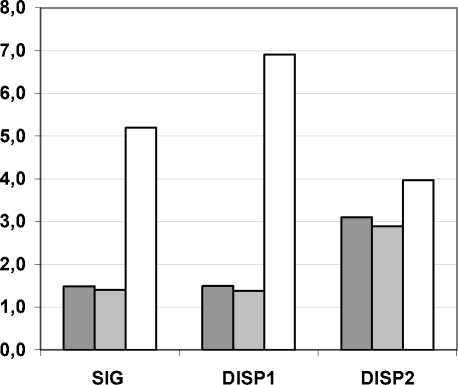
LINF

MEDF

GRAN

Рис. 3. Результаты сравнения предлагаемой обработки приходящего сигнала рассеяния (нелинейной фильтрации - GRAN) с методами линейной и медианной фильтраций (LINF, MEDF)

4.    Заключение

Проведенное исследование показывает, что предложенный подход позволяет дополнительно использовать лазерное зондирование атмосферы для решения задач по прогнозу устойчивости стратификации в приземном слое атмосферы. Как следствие, это позволяет прогнозировать уменьшение устойчивости метеоситуации, как более инерционного процесса, по упреждающему изменению характера выявленных структур оптических неоднородностей приземного слоя относительно устойчивой атмосферы.

Обобщая полученные результаты, можно говорить о выявленной возможности по структуре горизонтальных неоднородностей приземного слоя атмосферы судить о вертикальной динамике широкого комплекса метеопараметров и общей устойчивости метеоситуации.

Использование описанной методики измерений и обработки результатов позволяет ставить задачу краткосрочного прогноза метеоситуации по динамике структуры атмосферных неоднородностей (как предикторе), выявляемых в процессе измерений сигнала обратного рассеяния оптического излучения в горизонтальной плоскости приземного слоя атмосферы.