Использование математических моделей в неравновесной экономике с компенсирующим спросом
Автор: Лапшина М.Л., Лукина О.О., Лапшин Д.Д.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Экономика и управление
Статья в выпуске: 1 (83), 2020 года.
Бесплатный доступ
При моделировании неравновесной экономики поведение участников описывается такими же оптимизационными задачами, включающими критерий и внутренние технологические и бюджетные ограничения, как и в теории вальрасовского равновесия. Они лишь дополняются внешними ограничениями на покупку (или продажу) дефицитных (неходовых) продуктов. Известны различные принципы установления этих границ. Они могут быть фиксированными (жесткая схема рационирования) и не зависеть непосредственно от решений участника либо определяться выраженным им спросом (гибкая схема). Предъявляемый спрос на рационируемые продукты, как правило, не совпадает с вальрасовским. Будем называть его заказом. В известных моделях, заказ считается равным активному спросу. Понятие активного спроса успешно используется в моделях регулирования цен. Однако он не является объектом выбора участников, направленного на оптимизацию их критериев. Между тем представляется естественным, что производители и потребители, стремясь к максимизации полезности, могут свободно выбирать размеры заказов по собственному усмотрению...
Продукт, отрасль, параметры, функция, равновесие, баланс
Короткий адрес: https://sciup.org/140248326
IDR: 140248326 | УДК: 360 | DOI: 10.20914/2310-1202-2020-1-369-379
Текст научной статьи Использование математических моделей в неравновесной экономике с компенсирующим спросом
Экономика включает производителей и потребителей (участников). Каждый участник независимо от других выбирает поведение, максимизирующее его полезность при наличии внутренних и внешних ограничений. Последние
возникают вследствие того, что при негибких ценах спрос на некоторые продукты может не удовлетворяться полностью и разумный участник должен учитывать этот факт при оптимизации. В отличие от [3], где внешние ограничения носят субъективный характер, здесь им придается
This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License
вполне конкретный смысл: они определяются поставками соответствующего продукта. Заметим, что понятие поставки тождественно сделке в [3] и таким образом объем сделки формирует внешнее ограничение одного из двух участников. В предлагаемых моделях каждый из участников выбирает объемы заказов на необходимые ему продукты. Все заказы на один продукт поступают на единый рынок, на другой стороне которого собираются все данные по предложению этого продукта. Если суммарный заказ превосходит предложение, продукт дефицитен и его поставки рационируются. В противном случае заказы удовлетворяются полностью, рационируются поставки продавцов. В дальнейшем будет рассматриваться рационирование, пропорциональное величине заказов.
При любых разумных функциях рационализации реализуется принцип «больше закажешь, больше получишь». Осведомленный о дефиците и частичном выполнении заказов разумный участник, предъявляя спрос, потребует больше, чем ему в действительности нужно. Предъявляемые требования складываются при этом из двух частей: действительного и компенсирующего спроса, или заказа. Первый выражает действительные потребности участника, максимизирующие его целевую функцию в сложившихся условиях; второй предъявляется с целью компенсации недопоставок вследствие дефицита. Наличие и свободный выбор участниками величины их компенсирующего спроса являются характерной чертой описываемой экономики, поэтому будем называть ее экономикой с компенсирующим спросом (или компенсационными заказами).
Если бы полезность и бюджетно-технологические возможности не зависели от величины заказа, участник стремился бы заказать столько, чтобы внешние ограничения стали несущественными. Так как это невозможно при неравновесных ценах, то в таких моделях (модели с манипулированием [3]) рационализируемого равновесия не существует.
В настоящей работе предлагаются два типа моделей, в которых рост заказов влечет за собой рост издержек. Слишком большие заказы делаются невыгодными или невозможными.
В моделях первого типа понятие заказа не только отождествляется с выраженным спросом, но ему придается и обычный житейский смысл. Более того, предполагается, что при оформлении заказов некоторая их часть оплачивается в предварительном порядке в момент заказа. Если заказ удовлетворяется не полностью, плата за недопоставленную продукцию возмещается заказчику (при регулярных связях процесс возмещения принимает более завуалированную форму перерасчетов). В этом процессе предварительная оплата порождает вмененные издержки, влияющие на выбор оптимальной величины заказа.
Другой причиной издержек, порожденных дефицитом и растущих с величиной заказа, является присущая такой экономике неопределенность объемов поставок. Правила рационирования дефицитных продуктов и в рыночной и в централизованно управляемой экономике не являются писанными, и принцип пропорционального распределения часто нарушается. Участники обычно могут более или менее точно указать нижнюю- и верхнюю границу отношения поставок к заказам. В условиях комплектности производственных затрат неопределенность поставок порождает избыточные запасы, обслуживание которых требует дополнительных издержек. В моделях второго типа будет предполагаться, что финансовые возможности производителя ограничивают максимально допустимую стоимость таких запасов. Хотя мы будем использовать термин «’заказ” для моделей обоих типов, во второй модели предъявляемый спрос не обязательно оформляется как заказ поставщику.
Для экономики с компенсирующими заказами будет определено понятие равновесия, аналогичное [1–3], и приведены достаточные условия его существования. Модель с предварительной оплатой используется в работе для анализа воздействия таких макрорегуляторов, как налоги и государственные расходы на занятость и национальный доход. В этой части статьи мы следуем традиции, восходящей к работам [8–10]. Будет показано, что учет дефицитности промежуточных продуктов, которой пренебрегают авторы [8–10], существенно меняет результаты анализа.
В классическом режиме [3] при дефиците продукта и избыточности труда государственные расходы и уровень налогов не влияют на национальный доходи занятость, рост реальной заработной платы снижает выпуск. Для этого же режима ниже показано, что дефицит подавляет производство и потребление, т. е. с его ростом они снижаются. Поэтому мероприятия, увеличивающие спрос, снижают национальный доход и занятость, а увеличение налогов вызывает их рост. Хотя эти выводы получены для случая модели с предварительной оплатой, нетрудно убедиться, что те же оценки сохраняются и для модели, в которой ограничены запасы, порождаемые некомплектностью поставок.
Последняя модель возникла из попытки численного анализа падения уровня производства при переходе к рыночной экономике, когда цены еще неравновесны, а централизованного распределения ресурсов уже не существует.
В такой период важной причиной снижения выпуска является разрушение сложившихся хозяйственных связей. Выпуск продукции практически всеми производителями лимитируется не производственными возможностями или имеющимся спросом, а недостаточными поставками промежуточных продуктов. Сформулированная для леонтьевской экономики модель неравновесия с неопределенными поставками позволяет верифицировать значения параметров, характеризующих компенсирующие заказы на основе функции спроса или плана производства и данных отчетных межотраслевых балансов, и использовать ее для прогностических расчетов. Из-за направленности на прикладные цели все модели изложены в применении к леонтьевской экономике. Нетрудно видеть, что переход к более общим моделям неравновесия, в которых потребителей много, а каждый производитель может выпускать различные наборы продуктов, требует несущественных изменений.
Материалы и методы
Ограничимся для простоты изложения рассмотрением экономики леонтьевского типа. Она включает п +1 участника: «’конечного потребителя” и п отраслей, каждая из которых производит один продукт. Различные отрасли выпускают разные продукты. Для выпуска каждой единицы продукта j отрасль i затрачивает a единиц продукта i, j е N = {1,...,N}. Модель функционирования включает модели, описывающие поведение участников, и модель их взаимодействия. Описание начнем с последней. Каждый участник, исходя из своих возможностей и целей, заказывает производителю необходимую ему продукцию. Обозначим через z величину заказа участника j на продукт i. Суммарный заказ всех участников на продукт i n равен z( = У zy , где zi0 - заказ конечного потре-j=0
бителя. Пусть x – объем выпуска продукта i. Назовем продукт дефицитным, если z > xt. Обозначим через 5 = min {1, xj z,} средний для совокупности потребителей продукта i уровень удовлетворения заказов. Величину ^ = 5' 1 -1 будем называть показателем дефицитности. Заказ отрасли зависит прежде всего от планируемого ею выпуска, определяющего ее затраты промежуточных продуктов (ayx),. При отсутствии дефицита на рынке i, когда заказы z полностью удовлетворяются, естественно предположить, что заказы равны действительному спросу ry = ayx. Если же продукт дефицитен, то объем поставки будет меньше заказа, и для компенсации дефицита отрасль запросит больше, чем ей требуется. То же относится и к конечному потребителю, рассчитывающему на уровень потребления r0 = x,0. Не уменьшая общности, будем считать, что заказ включает два слагаемых, т. е.
Z j = ry + M j , i е N , j е N = {0,1,..., n}, (1)
где первое отражает действительные потребности участника, а второе направлено на компенсацию дефицита. Величины M будем называть компенсационными заказами. Последние должны удовлетворять естественному требованию
My > 0; My = 0, если to, = 0. (2)
Рынок дефицитного продукта управляется производителем, который распределяет продукт между заказчиками. Объем поставок каждому участнику не превосходит его заказа и зависит от возможностей производителя и заявок всех участников. Значения функция рационирования i -го продукта d, : R n + 2 ^ R n + 1, которой руководствуется производитель i , показывают количества продукта i , поставляемые всем заказчикам. Функции d удовлетворяют экономически понятным требованиям
0 ^ dy(x., z. 0»™» zin ) ^ zj v i,j, dy(X,z0»-»zn) = zj, если ю.= 0,
n
У d j ( X, zr 0
j = 0
X:, если ^ > 0, z ) = ,’ in
^ z , если ^ = 0.
Функции рационирования определяют фактические поставки (обозначим их v ), задающие внешние ограничения на выбор участников. Всюду в дальнейшем будем считать, что рационирование заключается в распределении дефицитных продуктов между участниками, пропорциональном их заказам, т. е. dy = ^zy , откуда vu = 5izij = zij min{1, xi / 1Lzu}. (6) j=0
Из (5) следует, что поставки, или внешние ограничения, зависят от выбора участников. Они могут по-разному представлять себе связь поставок с их действиями. Основное внимание будет уделено случаю, когда участники полагают, что их действия не оказывают влияния на уровень дефицитности продукта, т. е. величина vy пропорциональна их заказам у.. = 5. ( ry + My ), j е N , i е N , а уровень 5 фиксирован при выборе оптимального поведения.
Lapshina M.L. et al. Proceedings of VSUET, 2020, vol. 82, no. 1
Если участники учитывают влияние своих заказов на дефицитность, то vj=i (rj+ M )min 11, xi---— [, j e N, i e N (7)
j j j [ Zi( j) + rj+ Mj где величины z (i) = E zlk и xf рассматриваются k I как фиксированные.
Заказ является единственной информацией о спросе, поступающей на рынок. Поэтому разумно предполагать, что поставки v возрастают по аргументу z и убывают по z , что имеет место в (5). Соперничая друг с другом за поставки дефицитного товара, участники неограниченно наращивали бы свои заказы, если бы последние не влекли за собой издержек [4]. Рассмотрим следующую организацию процесса заказ-поставка-расчет. Прежде всего, этот процесс, так же как и фиксированные цены и рационируемое равновесие, относится к понятиям краткосрочного анализа, например, к изучению функционирования экономики в течение одного года. Пусть одно и то же количество продукта z заказывается каждые Т дней (или k раз в течение года). Заказ делается в начале, а поставка осуществляется в конце подпериода, через Т дней, причем поставляется величина v, v < z . Величина поставки v зависит от z : уменьшение z вызвало бы сокращение v , т. е. выбор z учитывает наличие дефицита и обеспечивает его доступную компенсацию. Предположим далее, что некоторая доля заказа оплачивается в момент заказа, а оставшаяся – после его поставки. Тогда в начале первого периода Т заказчик платит в pz, где р - цена заказываемого продукта; в - доля, оплачиваемая предварительно, 0 < в < 1. В начале каждого следующего периода заказчик платит в pz за заказ и доплачивает за поставку pv - в pz > 0, т. е. всего pv . В последнем цикле заказ не делается, и плата составляет pv - в pz • Сравним режим платежей заказчика с вариантом, когда компенсационных заказов нет и z = v . Различие состоит в том, что в начале года он платит дополнительно в p ( z - v ) и получает эту сумму обратно в конце года. Поскольку у участников всегда есть альтернативный вариант использования денег, например, положить их в банк и вернуть с процентами [6], вмененные издержки, порожденные компенсационным заказом, составят p в p ( z - v ) •
Теперь мы готовы сформулировать задачи участников. Производитель стремится максимизировать прибыль как разность между доходами от производства и его издержками, включающими вмененные, равные потерям от беспроцентного
кредитования поставщика, чем по сути является предварительная плата за нереализованные поставки. Отрасль j выбирает объем выпуска и величину заказа из решения задачи
Pjxj -ILpvu -wl - pE PyPiMy ^ max (8) i=1
при внутренних
0 < Xy < min {x™, Fy (ly )} и внешних ограничениях a,,x, < v,, V i, таких, что 5 < 1,(10)
ijjij xy< zj-
Здесь p = ( p ) - вектор цен; x; и Mtj - искомые объемы выпуска и компенсационных заказов; w – заработная плата за единицу труда; l – объем труда, использованного отраслью; p - норма банковского процента; в у - доля заказа на продукт i , оплачиваемая отраслью j в предварительном порядке, 0 < в < 1, Fj - производственная функция (определяет не чистый, как обычно, а валовый выпуск) отрасли j ; xm – верхняя граница выпуска, определяемая наличными производственными фондами.
Отметим, что второй член в (8), оценивающий материальные затраты, отражает тот факт, что все поставки (они не превосходят заказа), даже избыточные, оплачиваются. Последнее ограничение (11) исключает возможность перепроизводства неходового товара и гарантирует полную реализацию. Отметим, что внешние ограничения (10) и (11) удовлетворяют двум стандартным требованиям к моделям рационирования: никто не понуждается производить или потреблять больше, чем он желает, и рационируется только одна сторона каждого рынка. Назовем (8)–(11) задачей P .
Конечный потребитель, объединяющий домашние хозяйства, правительство и инвесторов, определяет свой действительный спрос X0 e R+ и компенсационные заказы Mo = (Mf0) e R^ , решая задачу u (x0, m) ^ max (12)
при условиях
EE p - ( v - 0 + в - 0 M i 0 ) + m 0 = B 0 , i = 1
m = m 0 (1 + p ) + lLp - в -0 M i 0 , (13)
i = 1
xi0 > 0, xi0 < vi0 для V i таких,что 5 < 1.
Назовем (12), (13) задачей С . В С целевая функция (12) зависит от вектора потребления x и денежной суммы m , передаваемой от бюджета B текущего периода в бюджет следующего. Эта сумма складывается из двух частей: сберегаемой m , которая может быть положена в банк под процент р и суммы L pt0^Mt 0, затраченной сверх необходимых платежей ∑ pv на предварительную оплату доли ( Д о) заказов. Эта сумма выплачивается в начале и возвращается в конце цикла.
Назовем экономикой-1 совокупность участников, выбирающих свое поведение из решения задач ρ j и С в случае, когда vij определяется условиями (6). Аналогично в экономике-2 v определяется условиями (7).
Равновесием в экономике-1 называется тройка n -векторов выпуска x * , потребления x * и показателей дефицитности ю - такая, что x * - решения задач P. , x * - решение С при S = (1 + ю *) - 1, а S* определяется (1).
Равновесием в экономике-2 называется пара векторов x * и x * и матрица
M* (n х (n +1)) - такие, что (x*, M* (j)) - решения P при фиксированных (xM*(к)) для к е N \ j, j е N, (x*, M*(0)) - решение С при фиксированных (x*, M* (к)), к е N.
Понятие равновесия-2 нуждается в некотором уточнении. В (7) входят переменные двух видов: одни выбираются отраслью j , другие ее поставщиками. При решении задачи P последние фиксированы. Возникает вопрос, что такое поставка отрасли самой себе и фиксирована ли величина в числителе правой части выражения для v . Будем рассматривать v как поставки одними предприятиями отрасли другим ее предприятиям, что имеет место в действительности. При этом каждое предприятие влияет на суммарный спрос, формирующий v , предложение же остается вне его воздействия. Поэтому будем считать, что величина x в формулах для v фиксирована так же, как и x в выражениях для v . Отсюда следует, что все v являются дробно-линейными функциями x и M .
Рассмотрим решения участников в экономике – 1. Из (6), (8) и (10), а также (12), (13)
следует, что оптимальные компенсационные заказы при заданных 5 и произвольных x , x0 удовлетворяют соотношениям
Mj = aj, , j е N ; M i о = x o ^ ., . E N . (14)
Положим b (Ю) = max {o, p} - n
- L pa ( 1 + рвю ) f и обозначим через i = 1
x j ( ю ) = arg max( b ( ю ) x - w 3.ф. ( x )), где ^. -функция, обратная F. , ю = ( ю ) е R n .
Пусть F определена в R n , дважды дифференцируема, F. (0) = 0, F‘(0) = да, F3 (да) = 0, F‘ < 0. Тогда xj (ю) = fj (w- bj (ю)), где fj - функция, обратная ϕ ′ , где xj (ю) = min{ x *(ю), Zj}, x* (ю) = min{ x ‘"(to), xy}
является единственным решением задачи P .
Из (14) следует, что задачу С можно представить в виде
u ( x 0 ,(1 + P ) m 0 + ]Е Р -' в '0 x i 0 ® ) ^ max (16)
i = 0
при условиях
IL P i (1 + e- 0 ® ) xi0 + m 0 = B 0 , x 0 E R n , m ^ 0
i = 0
Обозначим через x 0 ( ю ), m 0 ( ю ) решение (16).
Пусть u строго вогнутая функция, ненасыщаемая хотя бы по одному аргументу. Решения отраслей и конечного потребителя порождают непрерывное отображение δ ⇒ ω =
= (5i-1 -1) ^ x(ю), x0 (ю) ^ (S' = x. (ю) / Zi (ю)), переводящее компакт A = {5 е Rn : 0 < Д < 1 Vi} в себя. Здесь суммарный заказ z. (ю) = (1 + ю.)(x. 0 (ю) + L a.jxj (ю)). Неподвиж ная точка этого отображения S, существующая в силу теоремы Брауэра, определяет равновесие (ю , x0 (ю ), x(ю ) . Однако это утверждение в столь обшей форме мало полезно, поскольку всегда существует тривиальное равновесие S = 0, x* = x* = 0, M* = 0. Нетривиальное равновесие существует не всегда.
Утверждение 1. Показатели дефицитности ю равновесны тогда и только тогда, когда
n x^®") = x.0(ю>) + Laijxj(ю* )i E N. (17)
j = 1
M
Рассмотрим отображение T : R " ^ R " , заданное соотношениями T ( to ) = (1 + to )( x, 0 ( to ) + +iL a jixi ( to )) х ^ИГ1 - 1- .i = 1
Очевидно, неподвижная точка этого отображения является равновесной. Положим Q(to) = {to e R" : to’ < to Vi} для всех toe R" : r(to){to e Q(to): 3ito’ = to }, т- e- Г — северо-западная граница множества ^.(to) .
Утверждение 2. Пусть существует to 0 e R " такая, что 1) b ( to 0) > 0 V j e N , 2) T (0) < to 0; 3) функции T (Ato) j e N не возрастают по A при Г(ае ° ) для 1 < A < а ”1 и некоторого достаточно малого числа а > 0. Тогда отображение Т обладает неподвижной точкой to , причем < to < to .
Для экономики-2 аналогично (14) получим из (7), что
°- если z X j ) + r < Х
Пример 1.
Пусть
(
x
*
,
m
*
)
e
Arg
max{
u
(
x
,
m
):
px
+
m
=
B},
x
*
=
(
E
-
A
)
-
1
x
*
и
x
<
x
(0)
,
x
(0)
=
min{
x
m
,
x
j
(0)}.
Очевидно,
x
*
,
x
*
совместно с
to
=
0(
M
*
=
0)
являются равновесием-1 (равновесием-2) соответственно.
Пример 2
. Рассмотрим экономику-1 с
п
=
1 и заданными
в
=
в
=
P
,
B
q
,
Р
,
w
и удельными прямыми затратами
а
, 0
<
а
<
1. Пусть также
F(l) = kl°’5, xm = w . В силу (15) получим x1 (to) = 0,5k2pw-1 (1 - a(1 + pPto)) . Допустим, что du / dx0 > 0,5u I dm0 = 0. Тогда x0 (to) = Bo (p(1 + P®))-1 -Обозначим через Ф(®) = x0 (to) - (1 - a)x 1(®) функцию избыточного спроса (при to > 0). Из утверждения 1 следует, что в равновесии выполняются соотношения to > 0, Ф(to) < 0, toФ(to) = 0. Положим ц = 1 + Pto. Очевидно, Ф(to) = 0 при ц = (1 - a + ap ± ^(1 - a + ap)2 - 4apG) J2ap, 2 Bw где G =-------—7, и только при этих ц .
(1 -
a
)
k p
Равновесия не существует, если
G
>
Go
=
=
(1
-
a
+
ap
)(4
ap
)
-
1. При этом Ф
(
®
)
>
0
Vto
>
0
, т. е. невозможно добиться равновесия без изменения параметров (например, цен или заработной платы) или использования другой схемы рационирования. Если
G
<
G
o, то
O
(
to
)
<
0 при
to
e
(
to
1
,
to
2
), где
to.
=
в1
(ц
-
1),
Ц —
корни уравнения
Ф
(
to
)
=
0,
i
=
1,2, и равновесие существует. Пусть
ц
<
ц
. Если
ц
<
1, то
G
<
1
-
а
и равновесие достигается при
to
=
0,
Ф
(0)
<
0. При 1
-
a
>
ap
выполняется
ц
>
1. Если
ц
>
ц
>
1, то имеются два состояния равновесия при различных показателях дефицитности. Рассмотрим процесс установления равновесия
to
= Ф
(
to
), при котором дефицитность растет, если спрос избыточен, и наоборот. Равновесие
to
устойчиво относительно этого процесса, в чем можно убедиться с помощью функции Ляпунова (
to
-
to
)2, производная которой в силу системы отрицательна для
to
=
to
, 0
<
to
<
to
2. Заменяя в функции Ляпунова
to
на
to
2, нетрудно убедиться, что равновесие
to2
неустойчиво. Все возможные случаи расположения корней и области устойчивости легко представить графически, замечая, что
x
(
to
) - отрезок прямой при
to
e
[0,(1
-
a
)/
ap
P
], x0
(
to
) - кусок гиперболы. Всегда выполняется
Ф
((1
-
a
) I
apP)
>
0,, т. е.
to
<
(1
-
a
) I
ap
P
.
Опишем модель, по возможности сохраняющую структуру и обозначения, предложенные в [4]. Производитель находит объемы выпуска
x
(
to
) и заказа из решения задачи
p
(1 -
a
(1 +
pP<»))x
-
wl
^ max,
l
=
^
(
x
),
x
<
z
при
to
=0,
где ф = F 1 - функция, обратная производственной; z – суммарный заказ производителя и потребителей. Выражение (19) представляет собой задачу Pt в которой принято, что xm = да, а для M использовано его оптимальное значение (14). Созданная в процессе производства прибыль Q = p(1 - a)x(to) - —ф(x(to)). распределяется между потребителем и правительством. Доля у, поступающая потребителю, наряду с заработной платой и прочими источниками формирует доходную часть его бюджета. Потребитель решает задачу
u
(
x
0, (1
+
p
)
m0
+
p
Pto
x0
)
^
max (20)
при условиях
px
0, (1
+
Pto)
+
m
0 =
B
o =
m
+
—l
+
+Y
Q
—
t
,
l
<
l
0
(-).
p
Очевидно, (20) совпадает с
С
в форме (16). Предложение труда определяется вне оптимизации и считается известной гладкой монотонной функцией
l
реальной заработной платы. В дальнейшем будем, как правило, считать предложение неэластичным и равным константе
l
0
. Величина
т
- абсолютное значение налога в реальном выражении, который совокупность потребителей платит правительству. Деятельность последнего сводится к потреблению некоторой величины
g
, причем в случае сбалансированного бюджета
pg
=
т
+
(1
-
у
)
Q,
Потребление правительства приоритетно и не подвержено влиянию дефицита. В соответствии с утверждением 1 в равновесии соблюдается баланс
(1
-
a
)
x(
to
)
=
x0 (
to
)
+
g
. (21)
В предположениях примера 2 относительно производственной функции
F
решение (19) единственно и
Г
x
‘
(
to
)
=
min{
F
(
l
°),
f
(
p I —
(1
-
a
(1
+
p
^to
))] при
to
>0,
(22)
x (
to
)
= ( 7
[
min{
x
‘(
to
),
z
} при
to
=0.
Предположим также, что решение (20) единственно и дифференцируемо по параметрам. Существенную роль в дальнейшем играют знаки производных этого решения. Относительно этих знаков примем следующие предположения: 1)
d
x
I
дto
<
0, причем неравенство строгое, если
to
>
0, 2)
д
x
I
д
p
<
0, 3)
д
x
01 д
—
>
0, 4)
д
x
I
дт <
0. Первое и второе предположения выполняются при правильной постановке задачи, поскольку рост уровня цен и дефицитности реально снижает потребление. Третье и четвертое предположение также естественны, причем четвертое непосредственно следует из
д
x
I
дЕо >
0. Третье же означает, что с ростом заработной платы доход потребителей растет несмотря на снижение выпуска.
Рассмотрим сначала случай, когда сбалансированность бюджета не является обязательным требованием [9]. При этом вальрасовское равновесие определяется балансами по продукту и по труду ю = 0, x0(0) + g = (1 - a) f (1 - a) p/— = (1 - a)F(10 (—/p), где x0 (0) - функция параметров p, —, т, у и других. Пусть в соответствии с примером x убывает по р при фиксированных x и w/p. Тогда эти уравнения однозначно определяют равновесные p0, —0. Рассмотрим теперь ситуацию, когда предложение продукта и труда избыточно. В этом случае компенсационные заказы отсутствуют, и анализ ничем не отличается от традиционного [8]. Такой режим функционирования экономики реализуется при выполнении неравенства x0 (0) + g < (1 - a) min{F(10( —/p)), f((1 - a) p/—)}
Нетрудно убедиться, что это неравенство определяет область
К
на рисунке 1.
На луче Л = {y e R2 : y = A(p0, —0) Vy > 0} выполняется F(l0 (— I p)) = f ((1 - a)p I —) = const, в выше его f < F. В силу предположения о знаках производных спрос x падает вдоль луча. Поэтому граница К справа от равновесия достигается на f ((1 - a)p I —) и лежит выше луча Л. Слева от равновесия она достигается на F(l0 (— I p)) и лежит ниже луча Л . Если Y = 1 и l0 (— I p) = l0, то граница изображается вертикальным отрезком [(p0,0), (p0, —0)].
В общем случае она зависит от параметров и изображается отрезком кривой
(
p
1,0), (
p
0
,
—
0
)
. На границе Г4 области
К
спрос на продукт сбалансирован с предложением, т. е. слева от нее продукт дефицитен и заказ производителя включает компенсационную часть. Левая часть первого квадранта подразделяется на две области: нижнюю, где дефицитны продукт и труд, и верхнюю, где только продукт дефицитен. В традиционном анализе [4] граница между ними, очевидно, проходит по лучу
Л
.
Влияние дефицита на поставки промежуточных продуктов сокращает выпуск и спрос на труд и понижает границу между верхней и нижней областями. Сохраним за верхней областью ее обозначение
С
. Обозначим через Ф функцию избыточного спроса. В этой области он вычисляется как
Ф
(
ю
)
=
x
0
(
to
)
+
g
-
(
1
-
a
)
f
(
p
(
1
-
a
(
p
P<0
+
1
)
)
)
.
(23)
(
—")
С помощью (23) установим характер зависимости показателей выпуска, потребления населения и занятости от макроэкономических регуляторов: правительственных расходов g, налогов 1 - у и т , а также уровня цен р и заработной платы w. Интерес представляют эти зависимости в точках устойчивого равновесия ω , для которых Ф(^*) = 0, Ф‘(^*) < 0. Из условия равновесия Ф(®) = 0 с помощью теоремы о производной неявной функции отыщем знаки производных показателей как функций регуляторов. Легко проверить, что из предположений о знаках производных спроса x следуют неравенства дФ/дg > 0, дФ/дт < 0, д Ф/ду > 0, дФ/Sw > 0, дФ / дp < 0. Поэтому равновесное to* растет с ростом g, w и убывает с ростом р, т и 1 - у (при отсутствии требования сбалансированности бюджета).
Найденные зависимости не противоречат здравому смыслу: показатель дефицитности растет с ростом избыточного спроса, порожденного ростом заработной платы и правительственных расходов, и убывает с ростом цен, увеличивающих предложение и сокращающих спрос [5]. Последнее относится и к налогам. Сравним теперь влияние макроэкономических рычагов в области
С
в классическом анализе и в экономике с компенсационными заказами, когда производитель и потребители конкурируют друг с другом за поставки дефицитного ресурса. Рост правительственных расходов в классической экономике не оказывает влияния на производство, замещая потребление населения. В кейнсианском анализе (в режиме
К
) он стимулирует производство. В модели с компенсационными заказами рост правительственных расходов сокращает производство, национальный доход и занятость и вызывает еще большее сокращение потребления населения. Сказанное справедливо для вариаций
g
, не изменяющих режима
С
(или
К
) функционирования экономики. Если сокращение
g
приведет экономику из
С
в состояние, лежащее на границе
К
, то любое дальнейшее изменение
g
будет только сокращать национальный доход. Рост налогов и на потребителя, и на производителя действует в противоположном направлении. Уменьшая избыточный спрос, налоги улучшают условия снабжения производителей и влекут рост национального дохода и занятости. Заметим, что при этом растет и потребление населения за счет роста его доходов. Граница
Г
смещается влево,
to*
уменьшается. Если при этом
to*
обращается в 0, то достигнут
«’оптимальный” уровень налогов: любое их изменение при прочих равных условиях снижает национальный доход. Таким образом, соотношения цен и заработной платы, для которых выполняется баланс по продукту (т. е. (
p
,
w
)
е Г
), одновременно обеспечивают оптимальность государственных расходов и налогов с точки зрения занятости и национального дохода. Рост уровня заработной платы влечет такие же последствия, как и в классическом анализе, когда продукт дефицитен, а его производитель свободен от внешних ограничений, а именно снижения национального дохода, спроса на труд и занятости [7]. Надо только отметить, что рост дефицитности усиливает влияние роста уровня заработной платы в сравнении с классической ситуацией. Рост цен вызывает рост производства как вследствие роста его эффективности, так и из-за снижения дефицитности.
Рисунок 1. Геометрическое представление кривой
К
Figure 1. The geometric representation of the curve K
Следуя изложенной схеме анализа, можно рассмотреть и случай, когда госбюджет должен быть сбалансирован в любом равновесном состоянии экономики. Если баланс бюджета достигается за счет выбора подходящего налога на прибыль, то
у
=
1
+
(
т
-
pg
) /
Q.
В действительности нецелесообразность чрезмерного роста заказов объясняется не только вмененными затратами из-за предварительной их оплаты. Рост заказов порождает также увеличение запасов и издержек, связанных с их оплатой и обслуживанием. В нормально работающей экономике запасы создаются преднамеренно и служат для поддержания ритмичного производства в перерывах между поставками и при случайных сбоях графика поставок. Такого рода запасы увеличиваются в условиях дефицита. Однако нехватки и рационирование сами порождают запасы, возникающие вследствие некомплектности поставок. Правила рационирования при дефиците обычно неписаны, и пропорциональность поставок заказам, как и любая другая детерминированная функция рационирования, является лишь идеализацией реальности [10]. Более точным было бы считать уровень удовлетворения заказов случайной величиной или некоторым неопределенным числом, лежащим в заданных пределах. Если поставки неопределенны, никакими заказами производитель не может добиться их комплектности. Некомплектность же снижает выпуск, и часть поставленных продуктов оседает у производителя в виде непредусмотренных и, вообще говоря, нежеланных запасов. Назовем их непланируе-мыми. Объем непланируемых запасов так же неопределен, как уровень удовлетворения заказа. Будем считать в дальнейшем, что их максимальная величина ограниченна.
Сформулируем задачу производителя в экономике в условиях неопределенности. Пусть по-прежнему
x
выпуск продукта
i
,
z
– суммарный заказ на поставки
i
. Тогда
3,
=
x,
/
z,
назовем базовым уровнем удовлетворения заявок,
го
=
д
-
-
1
, как и раньше, показатель дефицитности. Назовем также
д,f
фактическим уровнем удовлетворения: заказов и
^
=
(
d
f
)
-
1
-
1
— субъективным коэффициентом дефицитности. Можно по-разному задавать область неопределенности фактических уровней удовлетворения. Поскольку должны выполняться условия
0
<
д
<
1
и
д
=
1
^
д =
1
, будем считать, что неопределенность субъективных дефицитностей тем больше, чем больше сама дефицитность, т. е. удовлетворяется условие
^
e
[(1
-
h
)
го
, (1
+
h
)
го
]
, где 0
<
h
<
1,
h
=
(
h
) - некоторый фиксированный вектор. Тогда
д
^
[
d
min
,
д
™],
где
(
д
1™)-1 =
д
+
h
«
,
д
ГТ1 =
д
-
h
^-
При неопределенности поставок величина выпуска также неопределенна, и производитель стремится максимизировать минимальный (гарантированный) выпуск, если его продукт дефицитен, или удовлетворить все заявки в противном случае. Полагая, как и раньше, что заказ производителя zy = a, (x. + M, ) получим из неравенств типа (10), (11), что минимальный гарантированный выпуск равен x1 = min{x1, z}, если toj = 0, где x1 = min <
Mij x,
; min------
Чтобы выбрать величину компенсационного заказа M , заметим, что наибольшее количество продукта i оседает в виде запаса у j в случае, когда поставка i осуществляется в максимальной пропорции д™, а фактический выпуск совпадет с гарантированным (24). Тогда прирост запаса i - продукта Sj = а^ б™ (My - (1 - h ) го^) • Подсчитаем прирост суммарной стоимости n запасов, s. = ^ ps^ , пренебрегая для про-i=1 стоты тем фактом, что хотя бы один продукт (лимитирующий) всегда используется полностью. Если максимально допустимый прирост запасов ограничен, то n
S
j
=
Z
"
д
tM
j
-
(1
-
h
i
N
x
)
<
B
j
,
(25)
i
=
1
где
,
=
р6ау
— удельные затраты на продукт
i
;
B
– граница допустимого прироста. Производитель выбирает величину компенсационных заказов
M
, решая задачу
M
ij
min-------> max
i
:
a
j
>
0
го
(1 +
h
)
при условии (25). Очевидно, максимум в (26) достигается, когда выражения M^ / (1 + h )го не зависят от i. Положим M = (1 + h)^k,. Тогда x1 = min{x", kj} j в силу (24), т. е. xj < k; Поскольку (21) определяет гарантированный выпуск, минимизируя максимальный прирост запасов, заметим, что избыток заказов kj > xj нецелесообразен, т. е. kj = xj. Из (26) следует, что kj < Bj (2h ^ ^ тч го, (1 + (1 - h )^) * )-1 Таким образом, оптимальный выбор производителя задается соотношениями x^ (го) = min {x1 (го), z3}, где x 1 (го) = min < x" n 2Ё "i l=1 Bj roh
My
(
ro
)
=
(1
+
h
)
rox
, (
ro
).
Дефицит порождает также непланируемые запасы у потребителей. Например, существующая система «’заказов” часто навязывает ненужные покупателям товары. Однако очень трудно оценить, какая часть излишних продуктов замешает в потреблении нехватку других, а какая откладывается впрок, образуя запас. В общем случае обозначим через
y
(
ro
)
e
R
^
вектор заказов конечного потребителя. Пусть, как и раньше,
x
0 (
го
) - вектор конечного потребления.
Утверждение 3. Тройка го е Rn, x(го) = = (x} (го*)) е R и x0 (го*) образует равновесие тогда и только тогда, когда го* - решение системы 1 + (1 + h )го А x, = x + i - > а у , i i0 1 + го и xo = y^, x = x (го), го > 0, i е N• 1+го Для доказательства достаточно заметить, что выражения для x и x непосредственно следуют из определения базового 5, компенсирующего спроса и суммарного заказа. Предположим, что фактический спрос x как функция показателей дефицитности го непрерывен и обладает свойством валовой заменимости xo(го') > xо(го) при го = го + «ej, а > 0, Vj * i, Vi
В (29)
ej
– орт
j
в
Rn
Утверждение 4. Пусть выполняется (29) и существует вектор го > 0, такой, что n
x
(0)
<
x
0
(0)
+
2
aijx j
(
го
)
V
i
, (30)
.j
=
1
x
i
1(
гo
)
>
x
i
0
(
гo
)
+
1
+
(1
+
-)го
2
a
j
x
m
V
i
(31)
1
+
го
j
=
1
Тогда рав
н
овесие (27), (28) существует, причем 0
<
го
<
го
.
Требования, гарантирующие существование равновесия, могут быть сформулированы по-другому. Пусть H(го) = (h(го)) - диагональ- ная матрица с диагональными элементами h (го) = (1 + (1 + h )го / (1 + го ), остальные h = 0. Очевидно, 0 < htJ < 1 + ht. Предположим, что матрица AH(го) продуктивна Vгo > 0.
Утверждение 5.
Пусть функция
(
E
-
H(
го
)A
)
-
1
x0 (
го
)
обладает свойством валовой заменимости, существует
го >
0 такое, что
x
1
(0)
<
(
E
-
H
(0)
A
)
-
1
x0 (
го
), x1 (
го
)
>
(
E
-
H(
го
) A
)
-
1
x0 (
го
).
Тогда равновесие существует. Это утверждение непосредственно следует из (12). Заключение
Модель экономики с некомплектными поставками и образованием непланируемых запасов, так же как и модель с предварительной оплатой заказов, может использоваться для анализа воздействия макроэкономических регуляторов на функционирование народного хозяйства. Модель (27), (28) удобнее для практических расчетов, поскольку включает 2
п
неизвестных параметра сферы производства
h
=
(
h
,) и
B
=
(
B
,),
i
,
j
е
N
, которые могут верифицироваться по наблюденным данным.
n
Из (28) следует, что величина
h
2
а^,
может
.j
=
1
рассматриваться как прирост запасов продукта i у всех участников – величина, фиксируемая в межотраслевом балансе. Если известна функция предъявляемого спроса у (го) и фактическое потребление, то уравнения (28) позволяют определить го и В. Предложенные методы и модели получили хорошую практическую апробацию и могут быть использованы не только для теоретического использования, но и для минимизации временных затрат при практической оценки экономической ситуации на предприятиях с учетом особенностей современного состояния рынка. Литература van Huellen S., Qin D., Lu S., Wang H. et al. Modelling Opportunity Cost Effects in Money Demand due to Openness. 2019. Gozgor G., Ongan S. Economic policy uncertainty and tourism demand: Empirical evidence from the USA // International Journal of Tourism Research. 2017. V. 19. № 1. P. 99–106. Лапшина М.Л. Аналоговые решения обратных задач моделирования линейных экономических систем // Системы управления и информационные технологии. 2003. № 1–2 (12). С. 23–25. Нельсон Р., Уинтер С. Эволюционная теория экономических изменений. М.: Финстатинформ, 2000. 98 с. Современный экономический словарь. М.: Инфра-М., 2017. 508 с. Na N. Mathematical economics. Springer, 2016. Blecker R. A., Setterfield M. Heterodox macroeconomics: models of demand, distribution and growth. Edward Elgar Publishing, 2019. Лукина О.О. Смена парадигмы управления инновационной деятельностью в условиях трансформации экономики // Вестник ВГУИТ. 2016. № 4 (70). С. 345–349. Клейнер Г.Б. К методологии моделирования принятия решений экономическими агентами // Экономика и математические методы. 2003. Т. 39. № 2. С. 167–182. Сумин В.И., Никитин А.Е., Смоленцева Т.Е. Оптимизация состава обеспечивающей информации для выработки управляющих воздействий // Современные проблемы науки и образования. 2015. № 2. С. 194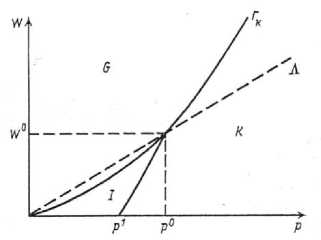
Список литературы Использование математических моделей в неравновесной экономике с компенсирующим спросом
- van Huellen S., Qin D., Lu S., Wang H. et al. Modelling Opportunity Cost Effects in Money Demand due to Openness. 2019.
- Gozgor G., Ongan S. Economic policy uncertainty and tourism demand: Empirical evidence from the USA // International Journal of Tourism Research. 2017. V. 19. № 1. P. 99-106.
- Лапшина М.Л. Аналоговые решения обратных задач моделирования линейных экономических систем // Системы управления и информационные технологии. 2003. № 1-2 (12). С. 23-25.
- Нельсон Р., Уинтер С. Эволюционная теория экономических изменений. М.: Финстатинформ, 2000. 98 с.
- Современный экономический словарь. М.: Инфра-М., 2017. 508 с.
- Na N. Mathematical economics. Springer, 2016.
- Blecker R. A., Setterfield M. Heterodox macroeconomics: models of demand, distribution and growth. Edward Elgar Publishing, 2019.
- Лукина О.О. Смена парадигмы управления инновационной деятельностью в условиях трансформации экономики // Вестник ВГУИТ. 2016. № 4 (70). С. 345-349.
- Клейнер Г.Б. К методологии моделирования принятия решений экономическими агентами // Экономика и математические методы. 2003. Т. 39. № 2. С. 167-182.
- Сумин В.И., Никитин А.Е., Смоленцева Т.Е. Оптимизация состава обеспечивающей информации для выработки управляющих воздействий // Современные проблемы науки и образования. 2015. № 2. С. 194


