Использование матрицы обмена к поиску равновесной ситуации на примере замкнутой экономической системы

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №6 2025

УДК 519. 865.3: 004.42                             

• 1)                , для j =    ;

• 2)    а      , для i =    , j =    .

Первое условие означает, что вся продукция j-й отрасли предназначена для обмена внутри системы, а второе — говорит о не отрицательности элементов матрицы.

Такую квадратную матрицу, для которой выполняются оба условия принято называть матрицей обмена [1].

Итак, рассмотрим матрицу обмена и поставим следующую задачу: необходимо определить такие цены на продукцию каждой отрасли, при которых вся рассматриваемая экономическая система будет находиться в равновесии. Под равновесием будем понимать, что отрасли с своем производстве и продаже равноправны (равносильны), по-другому, ни одна из них не обогащается за счет другой.

Введ ем в ра ссмотрение следующие параметры:

X i ( i = '. " 1, n ) — цена одной единицы продукции i -й отрасли:

• —    стоимость всей закупаемой ею продукции (расход i -й отрасли).

Для того чтобы i -ю отрасль могла существовать и развиваться, её расход не должен превышать дохода, т.е. стоимости произведённой ею продукции х i . С учетом этого получаем ограничения:

,

i =     .

При этом если искомые равновесные цены существуют, то система неравенств должна выполняться именно как система равенств. Покажем, что последнее утверждение верно.

Для этого совокупность всех цен хi (i =   ) одной единицы продукции каждой отрасли рассмотрим как вектор цен                   (он и является искомым).

Пусть числа               удовлетворяют условию (1), тогда подставим их в неравенства и затем сложим их почленно. При этом получим:

nnn

Z Z a j X 0 ^ Z x 0 ;

i=1 j =1

nnn

Z ( Z a ij ) x 0 ^ Z xf;

=1 i =1

nn

Z x j ^ Z x 0 .

= 1             i = 1

Но последнее неравенство с учетом условий 1 и 2 матрицы обмена справедливо только nn при выполнении знака равенства, т.е. Zx° =Zx° • Получили, что для чисел х°°,x°,...,x° J =1           i=1

n

E° a^xj = Xi , i = 1,n . j=1

Тогда в математической формулировке поставленная экономическая задача сводится к нахождению вектора                     , при котором существует единственная равновесная ситуация, т.е.

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №6 2025

Ax = x ;

Ax - Ex = 0;

(A - E) X = 0;

A - E = 0.

Последнее матричное равенство можно рассмотреть как A - 1 - E | = 0, а 1= Л, где Л — собственное значение матрицы А .

Проверим теперь, что Л = 1 действительно является собственным значением матрицы обмена, а для этого достаточно проверить, что .-: - лЕ = .' (где Л = 1), т.е.

	°и 1	а12     .	■     «1»
Л - ЛЕ| = и - 1 ■ £| =	°21	а22 — 1 .	■     а2П	= 0
	^1	апг     ■	■ апп - 1

Далее к первой строке прибавим все остальные строки и получим:

^=1^1-1 E^i^-l ... 2"=iain-l а21            а2г       ...       а2п ап1           ап2      ■■■      апп

n

Тогда элементы первой строки будут равны 0, т.к. в матрице обмена ^ а^ = 1. В итоге i=1

получаем матрицу с нулевой строкой, которая по свойствам будет равна нулю:

27=1^1-1	^i = l ai2 1   ■	■ 2Г=1ат-1		0	0     .	..     0
Я21	а22        ■	■        «2»	=	Д21	а22   ■	■ а2п	= 0
	^2      ■			«^1	^2  ‘	■■ апп

Таким образом, показали, что для матрицы обмена А собственное значение матрицы Л = 1, тогда остается найти соответствующий собственному значению собственный вектор

.

Найденный вектор и будет искомым неотрицательным вектором равновесных цен.

Приведем пример на нахождение такой равновесной ситуации: имеются 3 отрасли производства, каждая из которых выпускает один вид продукции. Система замкнута, и обмен внутри    системы    происходит    в    соответствии    с    данной    матрицей

/0,2 0,3 0,6 \ обмена                    . Определить вектор равновесных цен.

\0,4 0,2 0,3/

/-0,8   0,30,6 \

Найдём матрицу      :.

\ 0,4   0,2-0,7/

Составим матричное равенство:             , где          , т.е.

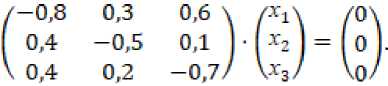
Последнее матричное равенство представим в виде системы уравнений:

f—0,8x1 + 0,3*2 + 0>6*з = 0;

j 0,4хг — 0,Sx2 + 0,lx3 = 0;

l 0,4х_х + 0,2x₂ — 0,7x₃ = 0.

Решив эту систему, получим, что она имеет бесконечное множество решений в виде:

³³ C ,⁸

28   7

C e R . Принимая !' = 2 ? ^l: : ^l: ^: .' :, получим x = • i :' <   :' 2 <  2 ? -.•:.

Таким образом, равновесные цены на продукцию каждой отрасли: , в котором коэффициент к можно рассматривать как множитель, связанный с денежной единицей.