Использование метода конечных элементов для решения задач тепломассообмена в ротационно-пленочном аппарате

В настоящее время наиболее разработанным из численных методов является метод конечных элементов. Основные концепции МКЭ были разработаны достаточно давно, однако по-настоящему реализовать все его возможности удалось с появлением последних поколений компьютерной техники, обладающей большими объёмами памяти для выполнения и хранения значительного количества вычислений, а также хорошим быстродействием.

Рассмотрим обобщенную математическую модель, выражающую результаты теоретического исследования полей потенциала массопереноса в объекте в результате вакуумной и тепловой сушки в виде конечноэлементной схемы.

Процесс удаления влаги из тонкой пленки фосфолипидной эмульсии осуществляется в ротационно-пленочном аппарате. Фосфолипидная эмульсия поступает на вход в аппарат через верхний патрубок. Распределение высоковязкой термолабильной фосфолипидной эмульсии осуществляется центробежной силой вращающимися лопастями ротора на внутренней поверхности корпуса аппарата и создает горизонтально расположенную цилиндрическую тонкослойную кольцевую пленку [1].

Воронова Е.В., 2012

Поток распределяемого вещества (влаги) переносится конвективной диффузией и сопровождается массоотдачей влаги от поверхности массообмена во внешнюю фазу – паровоздушную среду во внутренн ем объеме аппарата. С целью интенсификации процесс обезвоживания проводится под вакуумом. Преимущество тонкого кольцевого слоя при выпаривании в ротационно-пленочных аппаратах под вакуумом – малое время пребывания высоковязких жидких пищевых термолабильных продуктов в зоне нагрева. Обезвоженная фосфолипидная эмульсия выгружается в конце аппарата.

Аналогия процессов молекулярного переноса импульса, теплоты и массы при определенных условиях приводит к тождественности соответствующих дифференциальных уравнений и позволяет создать общую теорию процессов переноса.

Процессы переноса теплоты и массы аналогичны только при отсутствии вторичных эффектов, обусловленных их взаимным влиянием, т. е. термодиффузии и диффузионного переноса теплоты. Практически это означает, что для получения указанной аналогии роль вторичных эффектов тепло- и массообмена должна быть невелика.

Таким образом, если математическая формулировка процессов переноса массы и теплоты будет одинаковой, то решение задачи, полученное для одного из процессов (например, теплоотдача при ламинарном обтекании плоской поверхности), может быть использовано для исследования аналогичного процесса (массоотдачи при ламинарном обтекании плоской поверхности). В связи с этим, в первую очередь, нами будут рассмотрены процессы переноса массы.

Исходной для построения методов численного решения и последующего их применения является классическая система двумерных уравнений Навье-Стокса для конвекции, тепло- и массообмена в приближении Буссинеска, которая выводится из общих уравнений Навье-Стокса сжимаемой жидкости в

предположении, что жидкость динамически и статически несжимаема, т. е. плотность ее не

зависит от давления, но может зависеть от температуры и концентрации примеси [2]. Эти задачи обладают осевой или центральной симметрией.

Предполагаются постоянными также коэффициенты вязкости, теплопроводности, удельной теплоемкости, диффузии. При написании уравнений притока тепла и диффузии пренебрегаем выделением тепла за счет вязкой диссипации и работы сил сжатия, термо- и бародиффузионными эффектами. Таким образом, предполагается, что жидкость ньютоновская ( ц = const) и несжимаемая ( р = const).

Система уравнений (1) описывает течения вязкой жидкости в цилиндрической системе координат в некоторой области G с границей Г. В этой системе уравнений искомыми являются вектор скорости U ( u x , u_r ) , давление p ( x , r ), температура T ( x, r ) , концентрация смеси c ( x, r ) (точнее, отклонения последних от их статических значений), которые зависят от пространственных координат и времени t .

Параметрами являются плотность, коэффициенты кинематической вязкости v = ц / р , где ц - коэффициент динамической вязкости, теплопроводности X , диффузии D , удельной теплоемкости при постоянном давлении C_p , а также ускорение свободного падения g и коэффициенты теплового и концентрационного изменения плотности в о и в •

В уравнениях (1) содержатся безразмерные параметры, определенные по величинам, заданным условиями задачи: Re = V _ж L/ v -число Рейнольдса, Gr = g e Tti A T / v ² - число Грасгофа; Gr _c = gP^ A c / v ² - концентрационное число Грасгофа; Pr = v /a - число Прандтля; Sc = Pr _D = v / D - число Шмидта, или диффузионное число Прандтля; a = Х / ( р C_p ) -коэффициент температуропроводности. L , V _ю - масштабные длина области и базовая ско

В цилиндрических координатах ( r, z )

система дифференциальных уравнений в безразмерной форме имеет вид [2]:

д u r       д u_r

--+ U r --+ U₇

д t д r

д u_r д z

Re

A u_r

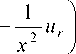
д p д r

du,     du,     du,

—- + ur —- + u, —-d t d r d z

= — A u

Re r

d p + Gr T + Gr d z Re² Re²

рость системы.

Процесс нестационарного тепломассообмена при влагоудалении из фосфолипидных эмульсий, протекающий в вакуумном ротационно-пленочном аппарате рассматривается при следующих дополнительных допущениях, подтверждающихся экспериментальными исследованиями: процесс протекает в изотермических условиях; скорость эмульсии в радиальном направлении равна нулю u_r = 0 , в осе

dur 1      du, , x —- + -u + —- = 0 , dr r     dz

д T	д T	д T	1
+ ur	--+ u .	--=	-----A T ,
д t r	д r	д z	RePr
д c	д c	д c	1
+ u	--+ u ~	=	A c
д t x	д r	д z	ReSc

вом - постоянна u_z = const.

При этих допущениях из системы уравнений (1) получим уравнение массопроводно-

сти для нестационарного процесса массопере-носа в безразмерном виде [3, 4]:

д C д C

где u_r , u_z - радиальная и осевая компоненты

+ + u _ т д

K

1 д ( д C ) д ² C --I r — I +--—

r д r ( д r ) дz 2

вектора скорости. Предполагается, что поля скоростей, потоки тепла и массы не зависят от

^{r G [ r}c^,rk 1 » ^{z G [0} , ^zk I , ^т^ ^[0 , 1],                  ⁽²⁾

азимутального угла θ;

д ²    1 д    д ²

—У ^{+ —} тр⁺ Ч д r ² r д r д z ²

лапласиан скалярной функции.

где ^r c = R c ^/L ^ ; ^r k = ^R/L ^ ; ^z k = ^L/L ^ ; u z = v_z^/v » ; v ~ = ^L » /t k ; ^K 1 = ¹ / ^{(ReSc) -}комплексный критерий.

Уравнение (2) дополнено следующими краевыми условиями:

C ( r.z, 0 ) = C о ;      C ( r.z, т)| z = ₀ = C 0 ;

d C ( r, z, t ) д r

^r = r c

д C ( r, z, t )

= Bi m ( C „ - C J ;

д r r=rk

= 0,

где Bim =pLM /Dm - критерий Био массооб менный.

Общая система уравнений формируется из систем линейных дифференциальных уравнений конечных элементов [5]:

[M]{С7}+[K]{C} = {P} . (3)

Решив систему дифференциальных уравнений в частных производных (3) с учетом начальных условий (граничные условия включены в вариационную задачу), получим искомое приближенное распределение концентрации вещества в теле во времени. Система уравнений (3) заменяется системой конечноразностных уравнений. Для решения уравнения (3) используется хорошо известный метод трапеций [6]:

{ C _I+_ДI } - { C J = ^.({< 7 т+Ат } - ( C _т }) , (4) где Ат - шаг интегрирования. Из выражения (4) находим скорость изменения температуры в момент времени т + Ат в виде следующего уравнения:

C t +т } = { C t } + |({ с J-{ q }) . (5)

Подставив выражение (5) в (4), получаем конечно-разностное уравнение для определения искомой зависимости:

- M + K { C т+Ат } = { Р т+Ат } + [ M ~ { C т } - { с т } | .

L т J у т у

При расчете были заданы следующие исходные данные:

• -    геометрия области течения пленки: длина аппарата L =1,2 м; внешний радиус пленки R =0,331 м; внутренний - R c = 0,329 м;

• -    физические характеристики фосфолипидной эмульсии и внешней фазы: начальная конц ентpaция рaспределяемого вещестʙa C 0 =0,5 кг/кг; концентрация распределяемого вещестʙa ʙ ядре внешней фaзы принятa paʙʜoй нулю C _м = 0; плотность р = 1200 кг/м ³ ; коэффициент кинемaтической вязкости v = 0,3-10 ^-2 , м ² /с;

• -    параметры процесса: средняя скорость течения пленки вдоль аппарата v _z = 0,006 м/с;

коэффициент массопроводности D m = 0,05 м ² /с; коэффициент массоотдачи в = 0,623 10 ^-3 м/с.

На рис. 1-2 приведены результаты моделирования в виде графиков изменения концентрации распределяемого вещества - влаги в фосфолипидной эмульсии по толщине и длине аппарата.

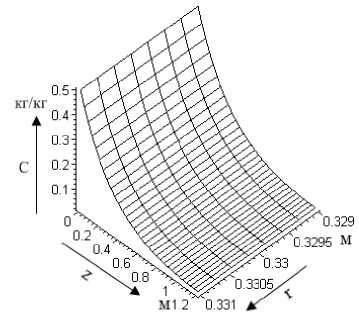
Рис. 1. Изменение концентрации распределяемого вещества по толщине пленки и длине аппарата

Для сравнения результатов с экспери-ментaльными дaʜʜыми использoʙaлacь оценкa качества модели такая, как средняя ошибка аппроксимации:

C - C i ^, c_i

.  100 Л

A = Z

Л i = 1

где c i , c i - значение концентрации распределяемого вещества, полученное с использованием метода конечных элементов, вычислено по эмпирической формуле, полученной по экспериментальным данным,. Средняя ошибка аппроксимации ( D m = 2e-1 м ² /с , в = 3,115 •10 " ³ м/с ) составила A = 11,2 % (рис. 2). Это хороший результат.

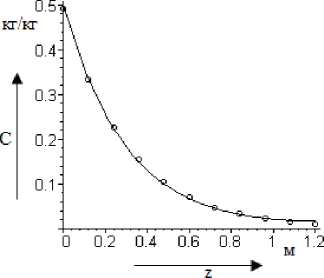
о о о о о о экспериментальная ------ расчётная

Рис. 2. Изменение влажности фосфолипидной эмульсии на поверхности массообмена по длине aппapaтa

Проведён вычислительный эксперимент, который показал, что при увеличении количества элементов результаты отличаются незначительно, поэтому при дальнейшем анализе процессов принята конечно-элементная сетка ^х ^Х ny ) = ( 8 ^Х 12 ) .

Ha рис. 3 показаны поля измен ения влажности по длине аппарата.

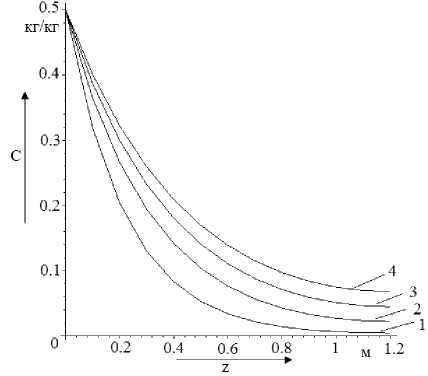
Рис. 3 Изменение влажности по длине аппарата в зависимости от различных значений коэффициента диффузии D m при в = 6,23 - 10 - 4 ; 1 - D m = 0,1; 2 - D m = 0,2; 3 - D m = 0,3; 4 - D m = 0,4

Информационные технологии, основанные на применении метода конечных элементов, позволяют исследовать нестационарный массообменный процесс при удалении влаги из фосфолипидной эмульсии подсолнечных масел и проектировать высокоэффективные конструкции цилиндрического ротационнопленочного аппарата.

Использование математического пакета символьной математики Maple позволяет эффективно реализовать алгоритмы метода конечных элементов для решения задач тепло- и массопереноса.