Использование метода сквозного счета для моделирования динамики систем с поверхностями раздела

Во многих задачах механики жидкости и газа возникает необходимость исследования динамики поверхности раздела между двумя несмешивающимися средами с разными свойствами. Вследствие нелинейности уравнений движения сплошной среды и зависимости поверхностных сил от формы границы раздела аналитическое решение подобных задач часто невозможно и необходимо применять численные методы.

Существующие подходы к численному моделированию динамики сред с поверхностями раздела можно разделить на следующие группы:

• 1)    методы, при использовании которых поверхность раздела аппроксимируется кусочно-заданным полиномом (метод «Front Tracking», метод граничных элементов);

• 2)    методы, основанные на отслеживании объема каждой фазы в расчетных ячейках, близких к границе сред (метод «Volume of Fluid» – VOF);

• 3)    методы сквозного счета (метод «Level Sset»).

Каждый из этих методов имеет свои преимущества и недостатки. Например, при использовании метода «Front Tracking» поверхность раздела можно аппроксимировать с высоким порядком точности, что позволяет проводить моделирование на относительно грубых сетках. Однако данный метод требует отслеживания топологии поверхности

раздела и применения специальных процедур при ее изменении. То же относится и к методу VOF.

В настоящей работе для численного решения задач с границей раздела сред используется метод сквозного счета. Этот метод, независимо предложенный в работах [1–3], основан на представлении двухслойной системы как одной среды с параметрами, зависящими от функции маркера. При этом поверхность раздела «размывается» в переходной слой с резко меняющимися параметрами. Поверхностные капиллярные силы аппроксимируются объемными таким образом, что объемная сила Fsv сосредоточена в узком переходном слое, где заметно отличны от нуля градиенты плотности (направление Fsv совпадает с направлением градиента маркерной функции; величина Fsv пропорциональна градиенту маркерной функции и кривизне поверхности; в предельном случае, когда переходный слой превращается в скачок характерных параметров жидкости, учет объемной силы Fsv приводит к обычному динамическому условию на поверхности раздела).

На основе указанных допущений выражение для объемной силы записывается в виде:

Fsv =-ak ( ф) 5 ( Ф^Ф ,

где ф - маркерная функция; 5 ( ф ) - дельта-функция Дирака; а - коэффициент поверхностного натяжения; к ( ф ) = div ( V ф / |V ф ) - кривизна поверхности раздела. В качестве маркерной функции в [2] использовалась плотность, а в [1, 3] – так называемая дистанционная функция, которая имеет противоположные по знаку значения в разных жидкостях; нулевой уровень дистанционной функции соответствует истинному положению границы раздела сред, а модуль этой функции пропорционален расстоянию до поверхности раздела.

• 2.    Основные уравнения

Рассмотрим поведение в поле тяжести двухслойной системы несмешивающихся жидкостей с различающимися плотностями р 1 , р ₂ и вязкостями п 1 , П 2 (индексы 1 и 2 относятся к нижней и верхней жидкостям соответственно) и деформируемой границей раздела. В соответствии с идеями метода сквозного счета [1–3] примем двухслойную систему жидкостей за одну жидкость с переменными плотностью и вязкостью и запишем уравнения динамики системы, введя объемную силу F_sv , аппроксимирующую поверхностные капиллярные силы:

(ри) + (uV\ pu = -Vp + — Div г +—pY+ — Fv, dtv ’ v ’             Re Fr We sv div Ш = 0, г = n

Г du du ,.) IT ⁺ IT dx. ox.

ji

Здесь й - скорость, p - давление, т - тензор вязких напряжений, у - единичный вектор, направленный вертикально вниз, g – ускорение свободного падения, ρ ( φ ) – плотность, η ( φ ) – динамическая вязкость. Уравнения записаны в безразмерной форме, в качестве единиц измерения длины, скорости, времени, плотности, вязкости, давления использованы следующие величины: L , U , L U , ρ ₁, η ₁, ρ ₁ U ² , где L и U соответственно характерные линейный размер задачи и скорость жидкости. Уравнения содержат следующие безразмерные параметры: Re = ρ ₁ LU η ₁ - число Рейнольдса; Fr= U ² gL – число Фруда; We = ρ ₁ LU ² α – число Вебера.

Объемная сила Fsv определяется выражением (1). В качестве маркерной функции в настоящей работе, как и в [1, 3], используем дистанционную функцию. Значения плотности и вязкости определяются по дистанционной функции с помощью выражений

ρ ( φ ) = λ + ( 1 - λ ) H ( φ ) , η ( φ ) = µ + ( 1 - µ ) H ( φ ) .

Здесь λ = ρ ₂ ρ ₁ , µ = η ₂ η ₁ , H ( φ ) – функция Хевисайда:

0,          φ < -ε, H (ф)=к . 1+ф+isin И^А,  ф ^е,                                (4) с п 1,           φ>ε, где ε - полутолщина переходного слоя.

Ограничимся рассмотрением двумерных решений. В этом случае можно ввести функцию тока ψ и плотность момента импульса Ω , при этом давление исключается из числа определяющих переменных [2]:

u_z = 0,

∂ ψ u = , x _{∂ y}

uy

∂ ψ ∂ x ^,

Q = ( rot р й ) _г .

Подстрочные индексы в выражениях (5) обозначают соответствующие компоненты завихренности плотности импульса и скоростей. Применяя операцию rotz к уравнениям движения жидкости (2) и используя (5), получаем уравнения движения в терминах плотности момента импульса и функции тока:

∂Ω ∂ t

= -^^rot ( ^{Div T} )_г —з (а у , р ) - -1 ^др + -^rot ( F s _V ) , Re          ^z             Fr ∂ x We ^z

ℑ ( ω , ψ , ρ )

' д^д у -д^д у ^ -d p < d 2 у ду + ду ду ' _v d x d y d y d x ) d x ^ d x d y d x d y ² d y _v

+ д р < д ² у д у + д ² у д у ^Л д y ^ д x д y д y    д x ² д x ^

f ^д р ^д ^ +

У d у ^d у

др V ) - р а У + а>' д x д x ) ^р [ д x² д x ² J

Для замыкания этой системы уравнений необходимо добавить уравнение переноса для дистанционной функции

∂ φ ₊ ∂ φ ∂ ψ _- ∂ φ ∂ ψ _{= 0} ∂ t   ∂ x ∂ y   ∂ y ∂ x

Из свойств функции Хевисайда следует, что ∇ H _ε ( φ ) = δ ( φ ) ∇ φ . В результате слагаемое в уравнении движения, содержащее объемную силу, можем переписать в виде

1             1 f дк днЕ дк днЕ rot (Fsv ) =^       ' -У’

We z We ^ д x д у    д у д x )

где кривизна поверхности k вычисляется по формуле

k = S ^{- 32}

дф у д 2 ф ₊ д x J д у²

^лд ф Y ^{д2 ф} - 2 д ф д ф ф^ £ _v д у ) д x ² д x д у д x д у

дф У+(ф У дx у у ду ^

• 3.    Численный алгоритм

Алгоритм численных расчетов был следующим. Пусть на данном временном слое заданы поля Ω ⁿ , ψ ⁿ , φ ⁿ , и их необходимо определить на следующем слое по времени _Ω n + 1_, ψ n + 1_, φ n + 1_.

Решая уравнения (6) и (7), рассчитаем значение функций Ω ^{n + 1}, ψ ^{n + 1} . Для аппроксимации производной по времени в уравнении (6) используем схему Кранка-Николсона:

Ωn+1 =Ωn+ 12∆t(ℜn+1+ℜn)+∆tΝn, где ℜn - конечноразностная аппроксимация нелинейного слагаемого и слагаемого, описывающего диффузию импульса; Νn – аппроксимация объемной капиллярной силы на границе раздела сред и силы тяжести; ∆t – шаг по времени.

С помощью уравнения (8) получаем значение дистанционной функции на следующем временном слое φ ^{n + 1} . Производную по времени в этом уравнении аппроксимируем по схеме Адамса второго порядка:

φ ^{n + 1} = ³ φ ⁿ - ¹ φ ^{n - 1} +∆ t ∏ ⁿ , 22

где ∏ _i ⁿ _j - конечноразностная аппроксимация правой части уравнения (8). В начале расчетов φ ^{n - 1} неизвестно, поэтому первый шаг по времени делаем по явной схеме первого порядка точности.

Далее производим процедуру уточнения дистанционной функции с целью уменьшения сеточной диффузии решения. Описание данной процедуры приведем ниже.

По уточненному значению дистанционной функции из формул (3) находим поля плотности и вязкости на новом временном слое.

Для повышения точности и сокращения времени вычислений расчеты проводились на многопроцессорных компьютерах с использованием параллельных вычислений и адаптивной сетки. Коммуникации между расчетными узлами осуществлялись с помощью библиотеки MPICH2, реализующий интерфейс передачи сообщений (MPI – The Message Passing Interface). Для построения адаптивной сетки использовался пакет Paramesh [4, 5], написанный на языке Fortran 90.

В пакете Paramesh исходная расчетная сетка делится на блоки одинакового размера. Затем проводится процедура адаптации сетки под решение – «Adaptive Mesh Refinement (AMR)»: в областях, где необходимо проводить вычисления с более мелкой сеткой, создаются новые блоки сетки. В результате строится древовидная иерархия блоков сетки. При этом независимо от местоположения блока в иерархии вычисления в нем можно проводить по одному и тому же алгоритму.

Пакет Paramesh содержит процедуры, которые распределяют блоки сетки по расчетным узлам так, что минимизируются межпроцессорные коммуникации. При выполнении расчетов по явным схемам пакет автоматически выполняет интерполяцию решений на границах блоков. Адаптация сетки в настоящей работе проводилась таким образом, чтобы обеспечить максимальную плотность узлов вблизи границы раздела сред.

Уравнения для плотности момента импульса (6) и функции тока (7) решаются неявно методом сопряженных градиентов (Bi-Conjugate Gradient Stabilized) с использованием процедуры предобуславливания. Расчеты осуществляются с помощью библиотеки Aztec [6], которая позволяет эффективно решать системы линейных уравнений с разреженной, распределенной по вычислительным узлам, матрицей.

Пространственная дискретизация уравнений проводится методом конечных объемов. При использовании этого метода расчетная область делится на конечное число контрольных объемов. В центре каждого контрольного объема на основе интегральной формы уравнений сохранения вычисляется значение переменной. Поверхностные и объемные интегралы аппроксимируются с помощью конечных разностей второго порядка точности.

• 4.    Процедура уточнения дистанционной функции

В ходе расчетов на каждом шаге по времени проводим коррекцию нулевого уровня дистанционной функции и толщины переходного слоя, размеры которого поддерживаем постоянными. Данная процедура позволяет, не изменяя положения границы раздела сред, свести к минимуму сеточную диффузию решения и размывание границы раздела, а также делает более гладким поведение дистанционной функции в пределах переходного слоя.

Теоретическое обоснование и описание основных уравнений, используемых для процедуры уточнения дистанционной функции, взяты из работы [7] и здесь не приводятся. Ограничимся лишь описанием численного алгоритма данной процедуры.

Во всей расчетной области решаем уравнение вида

^T = sign ⁽ ^ х^х -hi )

для некоторой вспомогательной функции Т у ( т ) с начальным условием Т у ( 0 ) = Ф ^{+ 1} • Здесь ф ^{+ 1} - значение дистанционной функции на n + 1-ом шаге по времени, полученное из уравнения (8), т - внутреннее время процедуры уточнения, подстрочные индексы i , j нумеруют узлы пространственной сетки. Необходимо решить уравнение (10) для т = 0... е . Значение функции T y ( е ) и будет являться уточненным значением дистанционной функции.

Опишем основные этапы решения уравнения (10), обозначая надстрочным индексом к номер шага по внутреннему времени т процедуры уточнения. Интегрирование по времени проводим по схеме Рунге-Кутта второго порядка точности.

Рассчитываем значения VT j | и

L ( ф , T j ) = sign h ( ф ) ( 1 -|v T j |) ,

где sign h ( ^ф ) = 2 ( Hh ( ^ф )^- V² ) , Hh ( ^ф ) вычисляется по формуле (4) при е , равном шагу сетки.

Определяем T y ^+V2 = T y + Ат [ L ( ф , T ij ) ] , где А т - шаг по внутреннему времени процедуры.

Рассчитываем |v T k ^+1/2|, получая L ( ф , Т ) из (11).

Вычисляем значение вспомогательной функции на новом временном шаге

^{T +} 1 = ^T   2 I L ^{( ф} , ^{T j )+} L ^{( ф} , ^T *^V2) ] .

Проводим коррекцию значений дистанционной функции вблизи поверхности раздела с целью минимизации изменения объемов сред:

T ij * ' = T j ^{+ 1} + A , ( T j ^{+ 1} ) н -( ф ) ,                                                              (12)

где H'( ф ) = d H /Э ф . Константу ^ ij для каждого узла расчетной области Vj определяем по формуле

J н - ( ф ) ( ф - T j ( т ) ) dV

А V-

^V ij

^;

/(н'(ф)) dV

^V ij

Для расчета V T k используем выражение

I vTj\ = 7( 3 T a x ) ² + ( d T а .у ) ².

Аппроксимацию пространственных производных в (14) производим по схеме второго порядка точности с процедурой уменьшения полной вариации (алгоритм Total Variation Diminishing). Интеграл в (13) вычисляем по девятиточечной схеме:

У f

V Vj

v j

( 11            ^

I I S f „ m„ + n I + 15 fj

V V m =- 1 n =- 1          v         /

h ²

.

На границах расчетной области пространственные производные вычисляем односторонними разностями с отступом внутрь расчетной области.

• 5.    Неустойчивость Релея - Тейлора

В качестве тестовой задачи использовалась задача неустойчивости Релея-Тейлора. Рассматривалась система двух жидкостей, находящихся в поле силы тяжести, сверху находилась более плотная жидкость. В такой системе при достаточно малых значениях поверхностного натяжения наблюдается нарушение механического равновесия. Более тяжелая жидкость начинает проваливаться через границу раздела, что приводит к перемешиванию жидкостей.

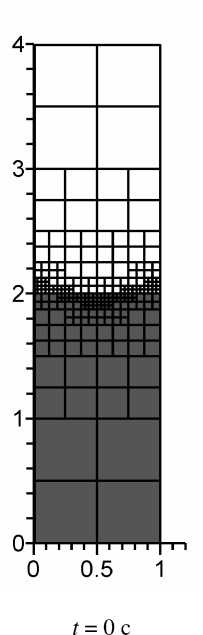
Расчеты поведения такой системы проводились для прямоугольной ячейки с отношением сторон 1/4. На вертикальных границах ставились условия периодичности, а на горизонтальных – условия прилипания. В начальный момент времени на границе раздела задавалось возмущение поверхности раздела сред в виде: 0,05cos ( 2 пх ) . Вычисления проводились для параметров, использованных в [8]. На рисунке 1 показаны формы границы раздела жидкостей для различных моментов времени. Полученные численные данные хорошо согласуются с результатами, приведенными в работе [8].

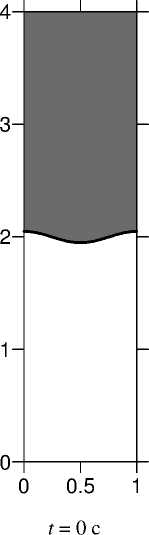
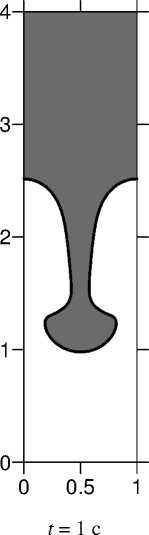
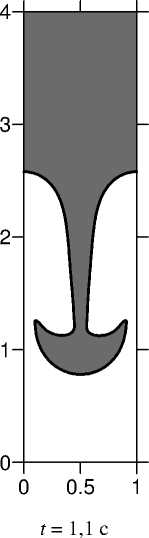
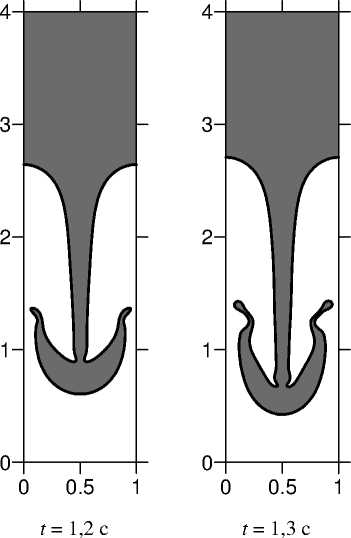
Рис. 1. Развитие неустойчивости Релея-Тейлора при We = 9,16, Fr = 0,102, Re = 391,4, Л = 0,13, ц = 0,13

4-

О11 । । । iiii । ।

О 0.5

t = 1,3 c

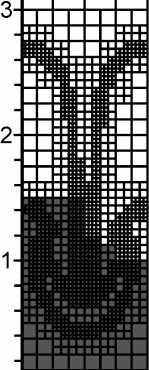
Рис. 2. Распределение блоков сетки по расчетным узлам в различные моменты времени

На рисунке 2 представлены блоки используемой при расчетах сетки в различные моменты времени, размер каждого блока 8×8 узлов. Как видно, в процессе счета количество блоков сетки увеличивается: в начале вычислений сетка состоит из 244 блоков, при t = 1,3 c количество блоков возрастает до 1334. Вычисления проводились на двух процессорах, на каждом шаге по времени выполнялась балансировка нагрузки на расчетные узлы. На рисунке серым цветом выделены блоки сетки, рассчитываемые на первом вычислительном узле, белым – на втором.

Проводилось также сравнение времен, необходимых для численных расчетов развития неустойчивости Релея-Тейлора с использованием однородной сетки размером 64×256 и адаптивной сетки с эквивалентной плотностью узлов вблизи границы раздела сред. Использование адаптивной сетки позволяет существенно сократить время, необходимое для проведения расчетов. Например, моделирование начального развития неустойчивости Релея-Тейлора ( t <  0,5 c) с использованием адаптивной сетки выполняется более чем в 3 раза быстрее, чем в случае однородной сетки.

• 6.    Периодические структуры на поверхности раздела несмешивающихся жидкостей при горизонтальных вибрациях

С помощью разработанного численного алгоритма, реализующего метод сквозного счета, проведено также моделирование периодических структур на поверхности раздела несмешивающихся жидкостей в замкнутой полости, совершающей горизонтальные вибрации конечной амплитуды и частоты.

Как известно [9, 10], в случае двухслойной системы бесконечных горизонтальных слоев несмешивающихся жидкостей при некоторой пороговой амплитуде скорости вибраций плоская поверхность раздела становится неустойчивой вследствие развития неустойчивости Кельвина-Гельмгольца и на ней возникает квазистационарный волновой

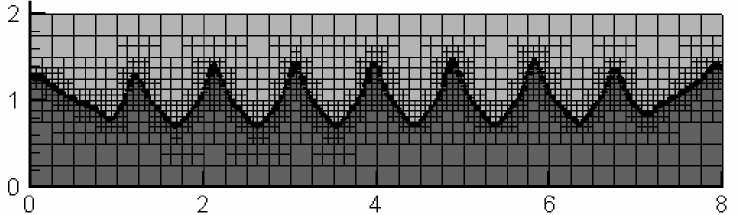
Рис. 3. Квазистационарный рельеф на поверхности двух несмешивающихся жидкостей при горизонтальных вибрациях с частотой 57,5 Гц, амплитудой 1,4 мм:

а – результат численного моделирования; б – данные эксперимента, проведенного в [10]

рельеф. В экспериментах [10] исследовались условия возникновения волнового рельефа и надкритическая динамика системы, состоящей из двух жидкостей: машинного масла и флуоринета FC-40. Вязкости этих жидкостей равны соответственно 1,87 Ст и 0,02 Ст, плотности – 1,85 г/см³ и 0,868 г/см³, коэффициент поверхностного натяжения a = 4 дин/см. Эксперимент проводился в прямоугольной кювете с размерами 20×20×140 мм.

На рисунке 3 приведены результаты расчетов, проведенных при параметрах, соответствующих экспериментам [10]. Как видно, численные данные о форме поверхности раздела хорошо согласуются с результатами экспериментов [10].

• 7.    Заключение

На основе метода сквозного счета разработан численный алгоритм для моделирования динамики двухслойных систем несмешивающихся жидкостей с деформируемыми поверхностями раздела. Написанная с применением технологий параллельного программирования программа позволяет проводить расчеты на многопроцессорных компьютерах с использованием адаптивной сетки.

Проведено численное моделирование развития неустойчивости Релея-Тейлора и периодических структур, возникающих на поверхности раздела жидкостей при горизонтальных вибрациях. Полученные численные данные хорошо согласуются с известными результатами численного моделирования и результатами экспериментов.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 07-01-00695).