Использование модели наклонно-слоистой среды при обработке данных вертикального сейсмического профилирования

Среди основных задач сейсморазведки следует отметить задачу оценки скоростного закона исследуемой среды (зависимость скорости распространения волны от глубины), на основе которой решаются задачи исследования околоскважинного пространства, уточнения структурных построений и задачи прогноза вещественного состава пород [1, 2].

Для обработки и интерпретации данных сейсморазведки обычно используется модель горизонтально-слоистой среды с однородными и изотропными слоями. Так как на распространение волны значительное влияние оказывают неоднородность и анизотропность слоев среды, а также форма и расположение границ раздела, то для удаленных пунктов взрыва (ПВ) такая модель во многих случаях становится неадекватной, а оценка скоростного закона, полученная с использованием этой модели, может содержать недопустимые погрешности [3]. В данной работе определяются границы области применимости наклонно-слоистой модели сред при обработке данных вертикального сейсмического профилирования (ВСП) на примере распространения прямой продольной волны (P-волны).

Рассмотрим модели слоистых сред со следующими параметрами (рис. 1): { h i } i =1,_, „ - толщина слоя в сечении скважины; { ф _i } i =1,..., _n - угол наклона границы; { V i } i =1,..., _n - скоростной закон.

а                                          б

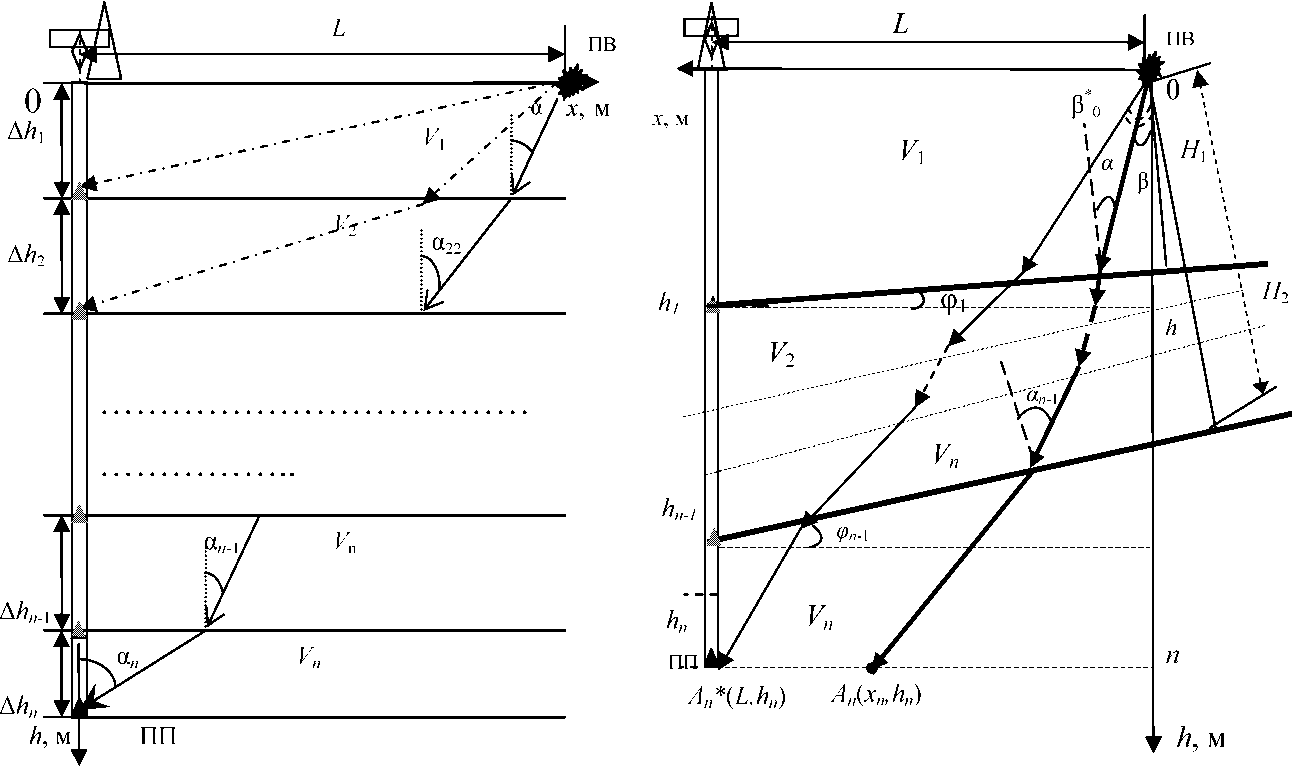
Рис. 1. Модели среды с n однородными и изотропными слоями: а - горизонтально-слоистая; б - наклонно-слоистая

Пусть наблюдение ВСП проводится в вертикальной скважине, возбуждение среды происходит на поверхности на расстоянии L от устья скважины, регистрация колебаний проводится в стволе скважины на всем интервале глубин.

Для изучения поставленных задач разработаны и реализованы алгоритмы решения прямой и обратных задач ВСП на основе представленных моделей горизонтально-слоистой и наклоннослоистой сред [3, 4]:

• 1.    Оценка годографа прямой продольной волны (времени прихода волны в заданные ПП).

• 2.    Оценка скоростной модели среды.

• 3.    Оценка угла наклона границ.

При решении задачи ВСП скоростной закон обычно оценивается на основе данных, полученных с ближнего ПВ, что позволяет обеспечить близкое к вертикальному распространение Р-волны. Часто скоростной закон с ближнего ПВ и скоростные законы, полученные с удаленных ПВ, существенно различаются. Далее будем считать, что единственной причиной несоответствия скоростных законов является наличие наклонной границы в среде. Рассмотрим влияние угла наклона границы на годограф прямой продольной волны и как следствие на оценку скорости на примере модели, параметры которой близки к реальным: количество слоев -10; мощность слоев в сечении скважины - 300 м; скоростной закон: V = 1409, 1339, 1297, 1685, 2016, 2443, 2533, 3284, 3005, 4030 м/с; удаление ПВ - 700 м.

Модели углов наклона

Номер модели	Глубина границы, м	Угол наклона ф, град
0	Горизонтально-слоистая модель (ф=0)
1	900	10
2	900	-10
3	2400	10
4	2400	-10

Исследовалось несколько моделей углов наклона границ (см. таблицу). В ходе исследова ния решались следующие задачи:

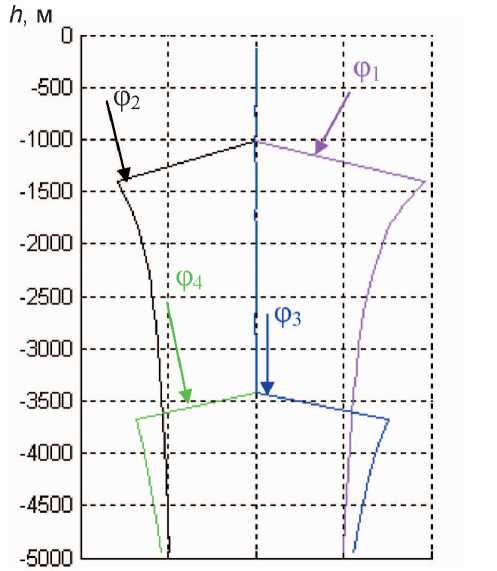
-0,010 -0,005     0   0,005 0,010 t, С

Рис. 2. Графики отклонений годографа для моделей, представленных в таблице

• -    для горизонтально-слоистой модели среды определялось время прихода P-волны t ^г( h );

• -    для каждой модели наклонно-слоистой среды определялось время прихода P-волны t ^н( h );

• -    рассчитывалось отклонение t ^н( h ) - t ^г( h ) (рис. 2).

Из результатов исследования следует, что наклон границы обусловливает нелинейное смещение годографа Р-волны ниже границы. Наиболее существенное влияние на годограф прямой продольной волны оказывает наклонная граница, расположенная ближе к дневной поверхности (на меньшей глубине), а по мере увеличения глубины влияние угла наклона уменьшается.

При использовании полученных годографов для решения обратной задачи на основе модели горизонтально-слоистой среды наблюдается смещение скоростных законов в локальном ин тервале глубин (рис. 3). Если ПВ находятся по разные стороны от скважины (углы наклона границ противоположны в направлении скважины), то в этом интервале наблюдается как положительное, так и отрицательное смещение скоростей (интервал локального разброса).

Таким образом, наличие локального разброса может служить признаком обнаружения наклонной границы. На рис. 4 приведены оценки скоростных законов по материалам ВСП, проведенного в одной из скважин Томской обл., полученные с использованием горизонтально-слоистой модели среды. В выделенных на рис. 4 областях наблюдается локальный разброс скоростей.

Если при обработке данных ВСП применяется горизонтально-слоистая модель среды, сле дует уточнить допустимые значения углов наклона границ, при которых эта модель может считаться адекватной. Очевидно, что в наибольшей мере на величину смещения годографа Р-волны и ошибку оценки скоростного закона помимо угла наклона оказывают влияние удаление ПВ,

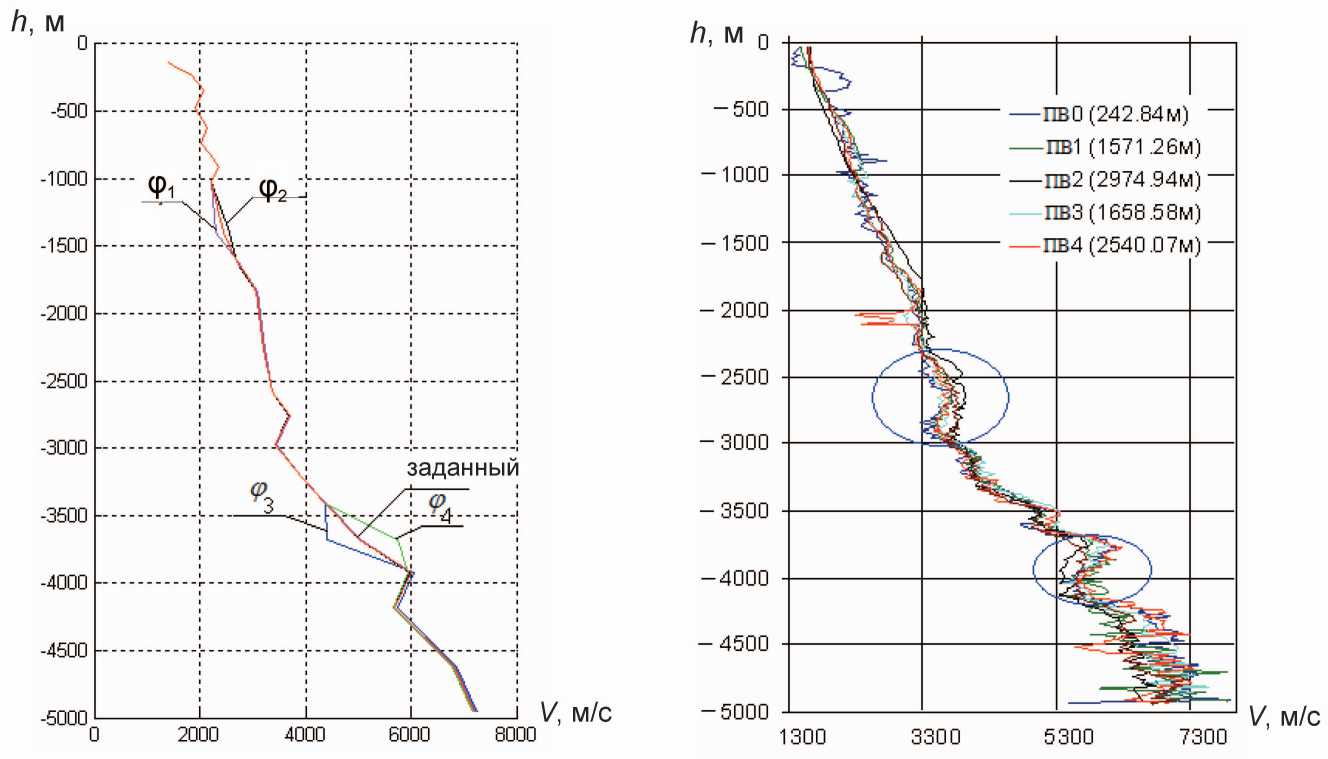
Рис. 3. Искажение скоростного закона при использовании модели горизонтально-слоистой среды

Рис. 4. Оценки скоростных законов, полученные с одной из скважин Томской области глубина залегания наклонной границы и дифференцированность скоростного закона среды. Проведен ряд экспериментов, позволивших оценить разрешающую способность метода ВСП по углу наклона границ. Применялся алгоритм, основанный на многократном решении прямой задачи для наклонно-слоистой среды с изменением угла наклона границы ф и ее глубины. В процессе решения определялся угол наклона границы ф (разрешающая способность ВСП по углу h, м

а

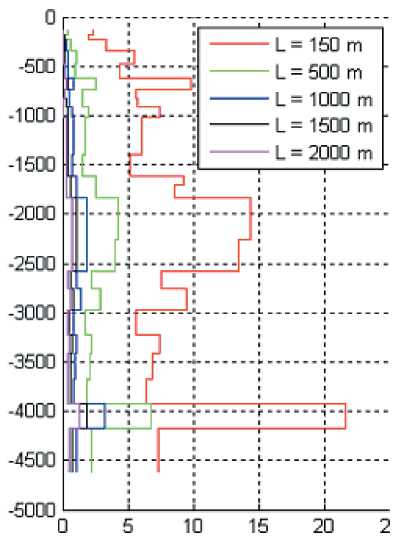
Рис.

. _            ф,град

5. Разрешающая способность ВСП по

б h, м

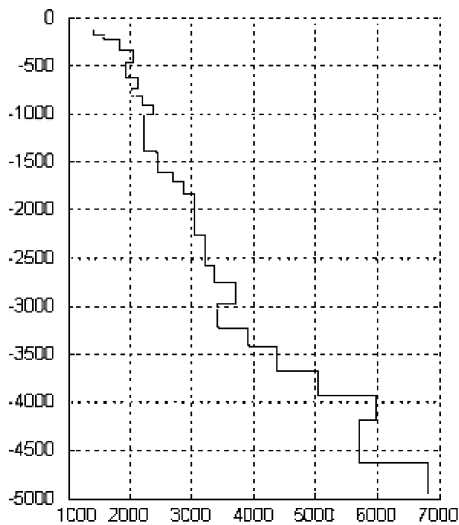
V, м/с наклона

для различных удалений ПВ ( а ) в среде со скоростным законом ( б )

наклона границ) на заданной глубине h , при котором отклонение годографа не превышало шага дискретизации, с которым получают материалы ВСП (обычно находится в пределах 0,5 ^ 2,0 мс). На рис. 5, а показано изменение разрешающей способности ф(h ) для различных удалений ПВ при принятом скоростном законе (рис. 5, б ) и шаге дискретизации, равном 1 мс. Видно, что при угле наклона границ менее 5 ° модель горизонтально-слоистой среды может быть использована только при обработке данных ближнего ПВ ( L = 150 м), а данные с удаленных ПВ не только можно, но и необходимо использовать для оценки и учета углов наклона границ, равных 1 ° .