Использование нейронной сети для обнаружения и идентификации помех при приеме шумоподобного сигнала

Введение                    Далее разность числа совпавших разрядов и

Шумоподобный полезный сигнал, излучаемый передатчиком, воспринимается приемником и обрабатывается с помощью аналоговоцифрового преобразователя (АЦП). Рассмотрим процесс более подробно. Обозначим каждый отдельный разряд М-последовательности, наблюдаемой на выходе АЦП, через X i , i = 1, N , где N – длина М-последовательности. На приемной стороне имеется также некоторая эталонная М-последовательность (образец), с которой принятые М-последовательности сравниваются. На основании сравнения принимается решение: была принята правильная М-последовательность или ошибочная.

Одним из методов принятия такого решения является использование автокорреляционной функции (АКФ) [1]. При этом, сравнивая поразрядно принятую и эталонную М-последова-тельность, получаем возможность отследить некоторые характеристики приема.

Так для каждого разряда x_i можно обнаружить факт его совпадения или несовпадения с разрядом e_i эталонной М-последовательности. Количество совпадающих разрядов обозначим N_y (уes), количество несовпадающих разрядов — N n (no). Очевидно, что N y + N n = N .

числа несовпавших разрядов сравнивается с некоторым заданным порогом P , т. е. для того, чтобы принятая М-последовательность была правильной, необходимо выполнение условия

N y — N n >  P,                                 (1)

где P = Np — уровень порога в интервале [0,1].

Проверка условия выше требует вычисления двух сумм. С точки зрения аппаратно-программной реализации можно упростить алгоритм проверки: достаточно считать только число совпадающих или только число несовпадающих разрядов. Действительно, с учетом условия (1) и того, что N y + N n = N , получаем следующие два условия:

N y > ( 1 + P ) N                             (2)

N n > ( 1 - P ) -.                                (3)

Так например для М-последовательности длиной 127 и порога p = 0.5 находим, что для того, чтобы считать принятую М-последовательность правильной, достаточно совпадения в 96 разрядах (с округлением до целых), либо число ошибочных разрядов не должно быть больше чем 31. Таким образом, для принятия решения о правильности приема М-последовательности доста

Число ошибок в

М-последовательности

Номер М-последовательности за период наблюдения Тп

Рис. 1. График числа ошибок в принятых М-последователь-ностях точно, например, подсчитать число ошибочных разрядов. С точки зрения аппаратно-программной реализации функции это дает выигрыш в количестве необходимых сумматоров.

Уже здесь возможно также применение нейронной сети в следующих двух случаях:

– при работе с аналоговыми сигналами до или внутри АЦП, однако это требует нетрадиционного подхода к проектированию АЦП;

– после АЦП для анализа качества приходящих М-последовательностей вместо АКФ используется нейронная сеть, такая возможность рассматривалась в [2; 3].

Расширим далее нашу модель введением некоторого периода наблюдения T_n (например, 1000 подряд принимаемых последовательностей) за поведением групп принимаемых М-последова-тельностей. Для группы последовательностей можем получить ряд дополнительных статистических характеристик. Для отдельной М-последо-вательности можем получить количество разрядов, в которых произошло несовпадение с эталоном. А поскольку число рассматриваемых М-последовательностей равно T_n , то для всего периода наблюдения получаем график изменения количества ошибок во времени (рис. 1), некий аналог «скользящих» графиков, для которых можно получать и другие характеристики, например линию скользящей средней.

От М-последовательности в целом можно перейти к более подробным статистическим характеристикам, например, для каждого разряда М-последовательности можно получить за период T_n количество n_i несовпадений в этом разряде. Отсюда, соответственно, можем получить частоту несовпадения f_{n , i} для i -го разряда.

Таким образом, имеем следующие статистические характеристики.

Скользящая частота несовпадений в i -м разряде:

f == n / Tu.(4)

n,

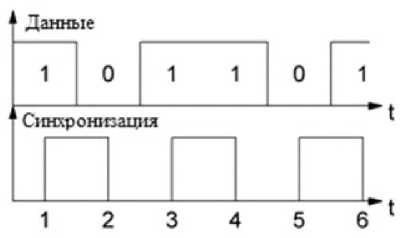
Рис. 2. Организация передачи данных

Скользящая частота совпадений в i -м разряде:

f y , i

_ yi _ Tn

~ гр ~ гр ^{- 1}   fn , i .

TnTn

Как уже отмечено, эти частотные характеристики являются динамическими, т. е. они формируются в изменяющемся времени (происходит смещение периода наблюдения вдоль временной оси). Поэтому даже при постоянном T_n частоты несовпадения или совпадения являются также функциями времени: f_{n , i} ( t ), f_{y , i} ( t ). Поэтому по каждому разряду можно еще получить график изменения частот за время периода T_n , который не всегда будет линейным (по сути дела, это некоторые скользящие средние с заданным периодом).

Поскольку частота передачи М-последователь-ностей в системах связи достаточно высока (порядка МГц), то подсчет числа совпадений и несовпадений (и соответствующих им частот) должен происходить достаточно быстро, чтобы не выходить за пределы возможностей аппаратуры приемного тракта.

Таким образом, сбор статистических характеристик позволяет нам получить матрицу числа ошибок, в столбцах которой представлены отдельные М-последовательности, обозначенные их номером в периоде наблюдения T_n , а номер строки соответствует номеру разряда М-последо-вательности. Суммирование для отдельной М-по-следовательности числа ошибок по всем разрядам дает также вектор ошибок по М-после-довательностям внутри периода наблюдения T_n .

Возникающие в процессе сеанса связи помехи могут иметь различную природу: импульсные, квазигармонические, флюктуационные (в виде белого шума) [4; 6; 7] и т. д. Влияние этих помех отражается на качестве приема М-последовательностей, увеличивая число ошибок в них. Можно утверждать, что в принятых М-последовательностях остаются следы действия помех того или иного вида. Предполагается, что для каждого вида помех форма этих следов разная. Какая именно, можно установить в эксперименте, примерная схема которого представлена на рис. 2. Распознать их вид можно при помощи нейронной сети. Полученный вектор числа ошибок в М-последовательностях можно подать на входы нейросети, а на выходе ее получать как минимум тип действующей помехи. Учет числа ошибок по отдельным разрядам может помочь получить и более точные способы распознавания.

1. Пример нейронной сети

Чтобы описать работу нейронной сети, необходимо понять, как работает отдельный нейрон [4; 5]. Если m-размерный входной вектор подается на вход нейрона, то работу нейрона можно представить функцией g (x)> xWT + b, (6) где W – вектор весов, который соответствует множеству входов; b – некоторый свободный член [10]

Очевидно, результат этого действия есть некоторое число. В реализации функции нейрона есть линейная часть, описанная выше (операции сложения и умножения векторов являются линейными) и нелинейная часть, представленная решающей функцией f ( g ( x ) ) .

Нейронная сеть представляет собой некоторую структуру из нескольких отдельных нейронов, работа которых показана выше. Все операции для вычисления значения выхода нейронной сети могут быть записаны в матричной форме, чтобы все вычисления выполнялись эффективно [5]. В соответствии с теоремой аппроксимации нейронная сеть способна реализовать более сложные функции, чем отдельный нейрон [8; 13; 16].

В процессе обучения нейронной сети ей представляются обучающие примеры. Значения выходов нейронной сети рассчитывается с учетом этих примеров, и затем используется также функционал качества нейронной сети. Использование обучающей информации позволяет изменить веса нейронной сети таким образом, чтобы обеспечить требуемое качество работы нейронной сети [16].

В качестве структуры нейронной сети предполагается использовать многослойный персептрон [5], имеющий один входной, один или несколько скрытых и один выходной слой. На вход каждого нейрона входного слоя поступают раз-

ряды М-последовательности x_i . Для внутренних слоев в обозначении y_j ^{( n )} верхний индекс – номер слоя, а нижний – номер нейрона в этом слое. Число k нейронов в разных слоях может отличаться. Весовой коэффициент синапсиче-ской связи, соединяющий i -й нейрон слоя n - 1 c j -м нейроном слоя n обозначим через w_ij .

Работа многослойного персептрона описывается следующей формулой:

( n ) y_j

( k n - 1

= f z w n y ( n ^{- 1 )}- P i

V i = 1

где f – функция активации нейрона (для многослойного персептрона обычно применяются гладкие нелинейные функции активации, например гиперболический тангенс); P_j – пороговый уровень j -го нейрона в слое n .

Полезны также такие показатели, как среднеквадратичная ошибка обучения и среднеквадратичная ошибка обобщения:

El =

E T =

Q L K n - ^

Q T K n - 1

QL

k

n

Ln z zyin’j -dj ,

Q T ( kn.          .

z z У " ¹ ’ - d i  ,

n

где QL – количество элементов обучающей выборки; QT – количество элементов тестовой выборки; Kn – число нейронов в выходном слое (n)j сети; yi – значение нейрона в выходном слое с номером i в выходном слое n, вычисленное для j-го элемента выборки; dij – значение нейрона с номером i в выходном слое n, вычисленное для j-го элемента выборки.

2. Влияние помех

Воздействие помехи приводит к тому, что в принимаемом сигнале изменяются его характеристики. Рассмотрим несколько типичных случаев [9].

Гармоническая помеха. На входе селективного тракта приемника действует аддитивная смесь сигнала и гармонической помехи:

U ( t ) = A_s cos ( to _st + 9 _s ) + A p cos ( to p t + 9 p ) ,     (10)

где A , to и 9 — амплитуда, частота и фаза; индексы s и p соответствуют сигналу и помехе.

На выходе селективного тракта получаем:

A o = V A 2 + A po + 2 A so A po cos ( Ato t ) ,          (11)

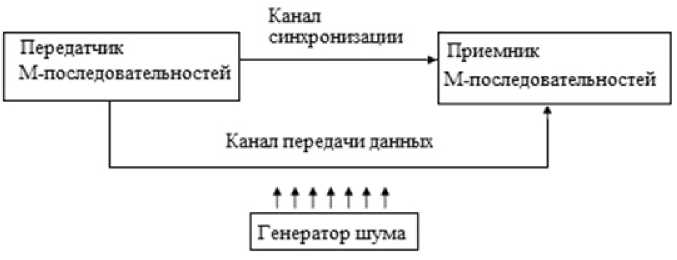
Рис. 3. Схема эксперимента по обнаружению помех

где Ato = | to s -to p — разность частот сигнала и помехи; индекс o соответствует выходу.

Фаза выходного сигнала изменяется следую- щим образом:

A po sin (^Ato t ) Ф ( t ) = arctg------------------.------.

A so + A po cos ( Ato t )

Импульсная помеха. Возникает в виде случайных импульсов. Соответственно, амплитуда помехи есть функция времени:

A o = V A so + A po ( t ) + 2 A so A po ( t ) cos ( 6 ) .          (13)

Изменение фазы сигнала на выходе зависит от фазы помехи:

Ф ( t ) = arctg

A po ( t )sin( 6 )

A so + A po ( t )cos( 6 )

Флюктуационная помеха. Часто представлена так называемым «белым шумом». При этом узкополосный случайный процесс записывается в виде

U n ( t ) = U n ( t )cos ( to o t -ф ( t ) ) ,                      (15)

где U n ( t ) — случайная огибающая; ф ( t ) — случайная фаза узкополосного колебания; индекс n соответствует шуму.

Распределение вероятностей мгновенного значения шумового напряжения U_n подчиняется нормальному закону:

² n 2

P ( U n ) = -_= e ²⁰ n ,                     (16)

• V 2non

3. Техническая реализация

где o n — дисперсия шума.

Распределение огибающей шума подчиняется закону Релея:

² n 2

P ( U n ) = -n e ^{2 o} n .                             (17)

^o n

Таким образом, можно отметить, что различные виды помех по-разному действуют на выходной сигнал, что закладывает основу для возможности распознавания типа помех.

Экспериментальная система связи состоит из передатчика и приемника сигнала [11; 12]. Используются платы Arduino Nano на основе микроконтроллера ATMega328p. Связь между передатчиком и приемником (рис. 2) осуществляется через синхронный интерфейс на частоте 20 кГц. Раз в секунду передатчик генерирует предварительно записанную М-последовательность на одном из своих выходных портов, сопровождая ее импульсами синхронизации (рис. 3). Приемник проверяет состояние ввода и сохраняет полученную битовую последовательность в память. Далее компьютер через адаптер uart-usb считывает ее терминальной программой для последующей обработки с помощью нейронной сети. В этом случае импульсы синхронизации передаются по проводам, а передаваемые последовательности - по радиоканалу [14; 15; 17].

Для тестирования были использованы M-последовательности длиной 31 бит.

Эталонной последовательностью была следующая:

Сравнение полученных M-последовательностей с эталонной дает следующие результаты (представлены только типичные М-последовательности): 1110010001010111101101001100000

N - N = 31 - 0 = 31 result = 1

yn

N - N = 30 - 1 = 29 result = 0.9354839 yn

N„ - N = 29 - 2 = 27 result = 0.8709677 yn

N„ - N = 17 - 14 = 3 result = 0.09677419 yn

N„ - N = 16 - 15 = 1 result = 0.03225806

yn

N - N = 13 - 18 = - 5 result = —0.16122903

yn

N - N = 15 - 16 = - 1 result = —0.03225806

yn

Полученные данные показывают, что нейронная сеть может быть реализована и обучена так, чтобы распознавать помехи, которые присутствовали в передающем канале, и определять характеристики достоверности полученных М-последовательностей не хуже, чем АКФ. Следующим шагом может быть использование нейронной сети для анализа следов помех в отклике приемо-передающего тракта, т. е. в совокупности получаемых в результате сбора статистики графиков скользящих частот числа правильно принятых или ошибочных разрядов.

Заключение

В процессе выполненных исследований получены следующие результаты:

• 1.    Рассмотрена возможность применения нейронной сети для обнаружения шумоподобного сигнала.

• 2.    Определены некоторые статистические параметры принимаемых М-последовательностей, и предложен механизм их формализации.

• 3.    На основании предложенной схемы эксперимента показана возможность обнаружения и идентификации действующих на систему связи помех в процессе передачи сообщения.

• 4.    Рассмотрены технические вопросы, связанные с постановкой и реализацией эксперимента.