Использование необыкновенной компоненты радиосигнала в задаче восстановления высотных профилей электронной концентрации по высотно-частотным характеристикам вертикального зондирования

В работе предлагается метод восстановления высотных профилей электронной концентрации в анизотропной ионосфере по данным вертикального зондирования (ВЗ). Входными данными являются наклонение магнитного поля и высотно-частотные характеристики (ВЧХ) для обыкновенной и необыкновенной волны (гирочастота вычисляется по разности критических частот необыкновенной и обыкновенной компонент). Выходные данные – высотный профиль электронной концентрации (или профиль плазменной частоты). Программа, реализующая данный алгоритм, была протестирована на большом числе модельных профилей, при этом восстановленные профили дают достаточно точное совпадение с исходными за исключением неизбежного для аппроксимационного метода расхождения в области «долины».

1971] в следующей последовательности: из зависимости h' ( f ) (для примера ВЧХ на рис. 1, б была смоделирована из профиля рис. 1, а с критической частотой F-слоя f ₀F2=4.58 МГц и высотой максимума h _mF2=206 км) делается переход к зависимости угла падения на слой от частоты при наклонном зондировании φ( f ) [Котович и др., 2006]:

ф( f ) = arctg

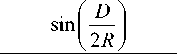
h '

Определение высот максимума E- и F-слоев

На первом этапе программа восстановления профиля рассчитывает высоты максимумов Е- и F-слоев. Для этой цели может служить известная эмпирическая формула вида

h m F2 =

M ( 3000 ) F2 + АМ

- 176,

которая известна, по крайней мере, в трех своих вариантах:

• а)    формула Шимазаки [Shimazaki, 1955], для которой Δ М =0;

• б)    формула Брэдли–Дадни [Bradley, Dudeney, 1973], где

0.18

АМ =

X _E — 1.4

в) формула Дадни [Dudeney, 1974]

АМ =

0.253

.

X_F - 1.215

E

f F2

Здесь X_E = —— .

^E     f 0 E

Параметр M ( 3000 ) F2 = МПЧ ( 3000 )/ f₀ F2 определяется из ВЧХ h' ( f ) методом Смита [Кияновский,

где D =3000 км – дальность трассы, R – радиус Земли.

Далее по закону секанса находится частота при наклонном зондировании (рис. 1, в ):

f нз ( f ) =    "'. ,                              (3)

cos ф( f )

где k =1 .116 – коэффициент сферичности Земли для D =3000 км.

Наконец, параметр МПЧ (3000) равен максимуму функции f HЗ ( f ) (рис. 1, в ).

Неточность определения параметра М (3000)F2 в данном случае может быть связана с тем, что метод Смита не учитывает магнитоионное расщепление, а производит пересчет ВЧХ вертикального зондирования в ВЧХ наклонного зондирования лишь в изотропном случае. Применение данного метода к обыкновенной компоненте ВЧХ не представляется корректным, как, например, показывает рис. 1, б : ВЧХ при ВЗ для обыкновенной компоненты (синтезированной для типичных значений гирочастоты f H =1.56 МГц и наклонения магнитного поля 19.5 ° ) существенно отличается от ВЧХ, рассчитанной в изотропном приближении (тонкая линия). Указанное различие приводит к тому, что применение метода Смита к обыкновенной    компоненте    ВЧХ    дает

М (3000)F2=19.3 МГц (рис. 1, в ) и высоту максимума, рассчитанную, например, по формуле Шима-заки, h _mF2=179.7 км с существенным отклонением от реальной высоты максимума профиля; тогда как для изотропного случая получаем М (3000)F2=17.8 МГц (рис. 1, в ) и соответственно h _mF2=206.4 км с достаточно точным совпадением.

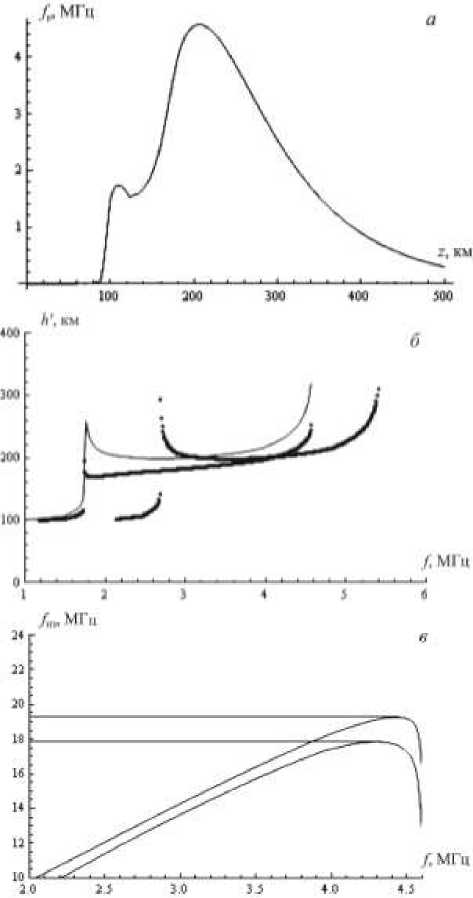
Рис. 1. Определение параметра МПЧ (3000) методом Смита.

Однако имеется возможность уточнения метода Смита для анизотропного случая. Для показателя преломления необыкновенной волны, согласно формуле Эпплтона–Хартри, имеем [Гинзбург, 1967]

На рис. 2 показаны обе части неравенства (5) в зависимости от времени группового запаздывания т ; моделирование проведено для необыкновенной волны для профиля, показанного на рис. 1, а , рабочая частота f =4.24 МГц. Очевидно, условие (5) нарушается лишь в окрестности точки отражения, где и ( т )=1 и 9 - 90 ° .

Условие (5) позволяет упростить выражение (4) до вида n2х -1--u-----.                                 (6)

1 - w cos 9₀

Критическая частота в этом приближении ff fх = и       „  - fco + cos 9o, в соответствии с

1 1 - w cos 9₀        2

известным соотношением [Гинзбург, 1967] f f х ” f c0 + ^, так как сos90 в наших условиях близок к единице, например, для рассмотренного случая cos19.5°=0.94.

Проанализируем погрешность при расчете действующих и истинных высот отражения, к которой приводит нарушение условия (5) в точке отражения. В табл. 1 приведены полученные в результате моделирования действующие высоты, вычисленные по формуле (4) и по приближенной формуле (6), а также соответствующие истинные высоты отражения. Существенное расхождение имеет место вблизи критической частоты, тогда как, например, для частоты f =0.834 f c x =4.5 МГц погрешность приближения составляет 0.8 %.

Таким образом, выражение (6) принимает вид изотропного приближения (со сдвигом критической частоты), для которого применим метод Смита:

n ² х - 1 - u x ,                                         (7)

где u_x

^{2 p} f ² ( 1 - w cos 0 0 )

Отметим следующее: тот факт, что ВЧХ необыкновенной волны близка к изотропному приближению со сдвигом частоты, позволяет также

n

x

2 u ( 1 - u )

2 ( 1 - u ) - w ² sin² 9 -   4 w² ( 1 - u ) 2 cos² 9 + w ⁴ sin⁴ 9

, (4)

применять для оценки высоты максимума слоя простой метод, описанный, например, в [Дэвис, 1973].

f2          f где u = y-, w = -y.

Отметим, что при вертикальном зондировании угол θ между волновым вектором и вектором магнитного поля остается практически постоянным и равным наклонению магнитного поля, для средних широт порядка 9 0 =20 ° (соответственно -20 ° при распространении назад). Исключение составляет лишь окрестность точки отражения радиоволны, которая будет исследована далее. В этих условиях выполняется неравенство cos²9 >> sin⁴9, а также, в силу условия w ² > w 4 , неравенство

4 w ² ( 1 - u ) 2 cos² 9 >>  w ⁴ sin⁴ 9.                  (5)

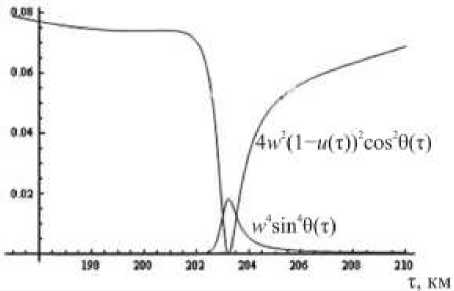
Рис. 2. Вклад окрестности точки отражения при моделировании с использованием формулы Эпплтона–Хартри.

Использование необыкновенной компоненты радиосигнала в задаче восстановления высотных профилей…

Таблица 1

Сравнение действующих и истинных высот отражения, полученных при моделировании с использованием формул (4) и (6)

f , МГц	h' , км, формула (4)	h' , км, формула (6)	точная высота отражения, км	прибл. высота отражения, км
3	203.7	203.4	152.7	154.1
3.25	199.7	200.2	158.1	159.2
3.5	197.8	198.5	162.2	163.0
3.75	198.3	199.4	165.7	166.4
4	200.3	201.6	168.9	169.6
4.25	203.2	204.6	172.1	172.8
4.5	207.3	209.0	175.3	176.0
4.75	213.1	215.4	178.8	179.6
5	226.0	230.8	183.4	184.6
5.25	252.3	264.4	190.7	192.9

Таблица 2

Определение высоты максимума различными методами

h mF2, км, исходный профиль	h mF2, км, формула Шимазаки	h mF2, км, формула Брэдли–Дадни	h mF2, км, формула Дадни	h m F2= h' x (0.834 f c x ), км
216.2	203.8	177.2	179.5	215.1
206.1	201.0	173.2	175.2	207.4
212.8	205.3	181.8	184.5	209.1
213.0	203.9	172.9	174.2	217.7
228.2	230.5	195.2	196.7	232.9
222.2	224.5	190.3	191.7	229.3
210.0	203.7	183.5	186.4	208.6
220.0	215.8	195.4	198.5	218.6
230.0	227.5	201.3	204.3	232.5
240.0	236.3	213.5	216.9	243.0
250.0	252.4	226.8	230.4	257.1
289.2	283.7	198.4	164.0	280.6
302.1	297.3	267.1	271.6	294.3
203.0	198.2	173.1	175.4	214.9
290.2	282.4	247.6	251.4	282.2

Как известно, в изотропном приближении для параболического слоя вида fP (z ) = f2

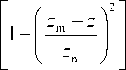
(zm – высота максимума, zn – полутолщина слоя, zm–zn – начало ионосферы) зависимость действующей высоты отражения от частоты можно определить аналитически: она имеет вид h ( f )= zm - zn + 1 fzn 1П fc+f . (9) mn n

² f c f c - f

Если в (9) потребовать выполнения условия h' ( f )= z m , то решение полученного трансцендентного уравнения будет иметь вид f =0.834 f c , т. е. действующая высота отражения на данной частоте будет приближенно равна высоте максимума слоя. Возникающая при данном подходе погрешность будет связана с тем, что профиль электронной концентрации в высотном интервале от z _m до истинной высоты отражения на частоте 0.834 f _c в большей или меньшей степени отличается от параболического.

Перечисленные способы определения высоты максимума слоя с использованием ВЧХ необыкновенной компоненты волны были протестированы на большом количестве профилей, взятых с ионозонда DPS-4, полученных по модели IRI-2000 или построенных с помощью аналитических функций. В табл. 2 приведены выборочные результаты для пятнадцати заданных профилей: для каждого из них моделировалась ВЧХ, которая затем обрабатывалась описанными выше методами.

Средний модуль абсолютной ошибки для формулы Шимазаки составил 5.6 км, для формулы h _mF2= h'_x (0.834 f _{c x} ) – 4.8 км. Для двух других формул он превысил 20 км. При выборе способа расчета высот максимумов E- и F-слоев, встроенного в программу, автор принял решение использовать формулу Шимазаки.

Подчеркнем, что на основе приведенных статистических данных о погрешностях автор не делает вывода о высокой точности формулы Шимазаки по сравнению с другими формулами. Утверждается лишь, что представляется более корректным применять метод Смита к ВЧХ необыкновенной компоненты, чем к ВЧХ обыкновенной, и в этом случае формулы Шимазаки и hmF2 = h'x (0.834f^) дают более точный результат, чем формулы Брэдли–Дадни и Дадни.

Восстановление профиля электронной концентрации

Гирочастота определяется из соотношения

f : ^- f co - f H [Гинзбург, 19 ^67] .

Для аппроксимации профиля электронной концентрации ниже максимума Е-слоя используется функция вида

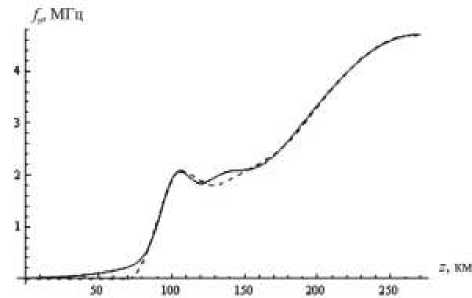
Рис. 3 . Пример восстановления профиля: штриховая линия – исходный профиль, сплошная линия – восстановленный.

f p ( z ) = f E exP

h m ^{E -} z

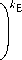
z ^ h _mE,      (10)

где f _E – критическая частота Е-слоя, определяемая по ВЧХ обыкновенной волны, высота максимума Е-слоя h m E вычисляется описанным выше методом. Параметры l E и k E находятся следующим образом: для каждой фиксированной степени k E производится перебор значений масштаба l E в диапазоне от 10 до 25 км с шагом 1 км, тогда как во внешнем цикле параметр k E принимает значения от 1.5 до 2.5 с шагом 0.1. По мнению авторов, указанные диапазоны покрывают значения l _E и k _E, необходимые для аппроксимации подавляющего большинства профилей ниже максимума Е-слоя функцией вида (10). Далее для каждой пары значений ( l _E, k _E) программа синтезирует ВЧХ обыкновенной компоненты волны с шагом 0.1 МГц в диапазоне от минимальной частоты, зафиксированной на ионограмме f min , до критической частоты Е-слоя f E . После этого методом наименьших квадратов находится наиболее близкое совпадение синтезированных ВЧХ с исходной, т. е. ищется минимальное значение

5 ( i , j ) = E ( h экс ( f ) — h'"'   ( f ) ) 2 ,            (11)

f где h' (f ) – действующая высота для экспериментальной ВЧХ на частоте f, h ' , синт(f ) – действующая высота для ВЧХ, синтезированной из профиля с параметрами (lEi, kEj). Пара параметров (lEi, kEj), соответствующая минимальному S(i, j), является искомой для подстановки в выражение (10).

Далее для восстановления профиля на высотах z ≥ h m E используется аппроксимирующая функция вида

k

( h F2 - z 1 0

fp (z) = fc0 exP -I           I +

V     ¹ o      J

и 1 .5≤ k 0 ≤3.5) и сравнение групповых задержек теперь происходит в частотном интервале f E < f < f c 0 . Третье слагаемое (12) оптимизирует аппроксимацию в области «долины»: высота h_z – это точка локального минимума функции

f _c0 exp

fhmF2-z \

V    1o    J

^{+ f} E exP

-

z - ^h m ^E

в интервале h m E< z < h m F2. Малые поправки Δ f и Δ z

во втором слагаемом возникают в силу того, что появление первого и третьего слагаемого в выражении (12) приводит к нарушению обязательных усло- df p (hmE)  a вий fp (hmE) = fe и --------= 0, характерных для

соотношения (10).

На рис. 3 показан пример работы алгоритма – исходный профиль (штриховая линия) был взят из модели IRI-2000. Имеет место неизбежное различие в области «долины», а также на малых высотах.

+ (fe -Af)exp

+ f z exP

hz - z

z

f z - hmE -Az

V        IE        .

kZ

+

Заключение

В работе предложен метод восстановления высотных профилей электронной концентрации, в котором для определения высот максимумов E- и F-слоев предлагается использовать необыкновенную компоненту радиоволны. Данный метод был проверен на большой базе различных высотных профилей с помощью численного эксперимента: из произвольного профиля синтезировалась ВЧХ, из которой предложенным методом восстанавливался профиль. Результат работы алгоритма сравнивался с исходным профилем, при этом в большинстве случаев полученный и исходный профили с достаточно хорошей точностью соответствовали друг другу.

Работа выполнена при поддержке гранта РФФИ № 11-05-00892-a и Минобрнауки РФ (соглашение № 8388).