Использование нетрадиционного сырья в пищевых производствах

Введение. Кондитерские изделия – удобный объект для обогащения микронутриентами, дефицит которых представляет собой серьезную проблему в нашей стране. Используемые при производстве кондитерских изделий компоненты содержат незначительное количество минеральных веществ и витаминов, которые в процессе технологической переработки разрушаются. При этом снижается пищевая, прежде всего? витаминная ценность продукта. Обогащение кондитерских изделий, таким образом, становится не только целесообразным, но и абсолютно необходимым. Одним из важных направлений повышения эффективности технологических процессов кондитерского производства является использование нетрадиционного сырья, ко- торое способствует повышению пищевой ценности изделий, экономии дорогостоящего сырья, интенсификации отдельных стадий производства [1, 2, 3].

Одним из нетрадиционных источников сырья являются морские водоросли, которые используются для приготовления пищевых и лечебно-профилактических продуктов, в качестве кормов и удобрений в сельском хозяйстве и сырья для химической промышленности. Они служат сырьем для производства агара, агароида, альгиновой кислоты, маннита и других продуктов. В настоящее время в производстве используется в основном ламинария, или морская капуста. Из морской капусты вырабатывают кулинарную и консервную продукцию, пищевой порошок, кормовую крупку, альгинат натрия, маннит.

Вследствие недостаточной изученности технологических свойств порошка из ламинарии он почти не используется в кондитерской промышленности [4]. В литературных источниках недостаточно полно отражено моделирование потоков сырья в технологической системе получения готовой продукции.

В этой связи изучение пищевой ценности мучных кондитерских изделий с включением порошка из ламинарии, а также моделирование потоков сырья в технологической системе получения готовой продукции, является актуальной задачей.

Цель исследований . Разработка рецептур функциональных кондитерских изделий с использованием порошка из ламинарии и моделирование потоков сырья в технологической системе получения готовой продукции на примере получения бисквитного полуфабриката.

Задачи исследований . Изучить влияние и определить оптимальные дозировки порошка из ламинарии на качество готовой продукции; разработать математическую модель потоков сырья в технологической системе на примере получения бисквитного полуфабриката с добавлением порошка ламинарии.

Объекты и методы исследований . Порошок из ламинарии, сахарное печенье и бисквитный полуфабрикат с добавлением порошка ламинарии.

Результаты исследований и их обсуждение . Для разработки рецептуры сахарного печенья с использованием порошка бурой водоросли ламинарии были взяты 3 образца изделия: с заменой муки на 2, 4, 6 % порошка из ламинарии. Для разработки рецептуры бисквитного полуфабриката с порошком бурой водоросли ламинарии были взяты 3 образца изделия: с заменой муки на 3, 5, 7 % порошка из ламинарии.

В технологической схеме производства разрабатываемых изделий введена дополнительная операция – введение порошка из бурой водоросли ламинарии. Пересчет рецептур полуфабрикатов с заменой пшеничной муки высшего сорта на порошок из ламинарии производится исходя из рецептуры контрольного образца. Замена осуществляется по сухим веществам заменяемого количества пшеничной муки высшего сорта идентичным количеством сухих веществ порошка ламинарии. Анализ готовых изделий проводился по органолептическим и физико-химическим показателям.

С добавлением порошка из ламинарии в печенье физико-химические показатели немного изменяются по сравнению с контрольным образцом, но остаются в норме по сравнению со всеми стандартами. В органолептической оценке изменились только параметры вкуса. Привкус морской соли растет с увеличением вносимой добавки. В печенье с 6 %-й заменой вкус явно выраженный, что мешает обычному вкусу печенья.

Дегустационная оценка разработанных образцов сахарного печенья с частичной заменой муки на порошок ламинарии на 2, 4, 6 % от массы муки проводилась по 30-балльной системе по методу Н.И. Ковалева. По результатам дегустационной оценки был сделан вывод, что образец сахарного печенья с добавлением 2 % порошка имеет в совокупности показателей наилучшие характеристики. С увеличением добавки порошка ухудшаются такие органолептические показатели изделий, как вкус, аромат, внешний вид и цвет изделия.

В результате проведенных исследований по внесению в бисквитный полуфабрикат порошка ламинарии можно сделать вывод, что оптимальным является внесение в бисквит 5 % добавки порошка из ламинарии. У бисквита с такой добавкой поверхность ровная, без надрывов, мякиш мягкий, нежный, равномерная поверхность. Следует отметить, что с внесением добавки такого процента не появился запах и вкус ламинарии. Была проведена дегустационная оценка разработанных образцов бисквитного полуфабриката с частичной заменой муки на порошок морской капусты на 3, 5, 7 % от массы муки. По результатам дегустационной оценки бисквитного полуфабриката образец с добавлением 5 % порошка ламинарии является оптимальным по качеству. С увеличением концентрации порошка ухудшаются такие органолептические показатели изделий, как вкус, аромат, внешний вид, цвет и структура.

Исходя из совокупности результатов проведенных исследований, были выбраны оптимальные дозировки порошка из ламинарии для разрабатываемых изделий. Для сахарного печенья оптимальная дозировка порошка составляет 2 % и для бисквитного полуфабриката оптимальной дозировкой 5 %. При данных дозировках изделия обладают наилучшими свойствами.

При расчете химического состава сахарного печенья и бисквитного полуфабриката был сделан вывод, что с внесением порошка снизилось количество углеводов, белков. Увеличились показатели таких элементов, как Na, K, Ca, Mg, Fe. С внесением порошка морской капусты в мучную группу кондитерских изделий, обогатились такими элементами, как Se, Zn, F, β-каратином, также присутствуют следы йода.

При расчете пищевой ценности сахарного печенья с 2 % добавлением порошка ламинарии установлено, что при употреблении 100 г печенья суточная потребность для взрослого человека составляет в белках 8,80 %, жирах – 12,28, углеводах – 18,99 %. При расчете пищевой ценности бисквитного полуфабриката с 5 % добавлением порошка установлено, что при употреблении 100 г бисквита суточная потребность для взрослого человека составляет в белках 12,61 %, жирах –7,14, углеводах – 20,87 %.

Для моделирования потоков сырья в технологической системе на примере получения бисквитного полуфабриката с добавлением порошка из ламинарии была разработана математическая модель исходя из заданных объёмов сырья, режимных и технологических параметров. Информационно-логическая модель технологической системы представлена на рисунке.

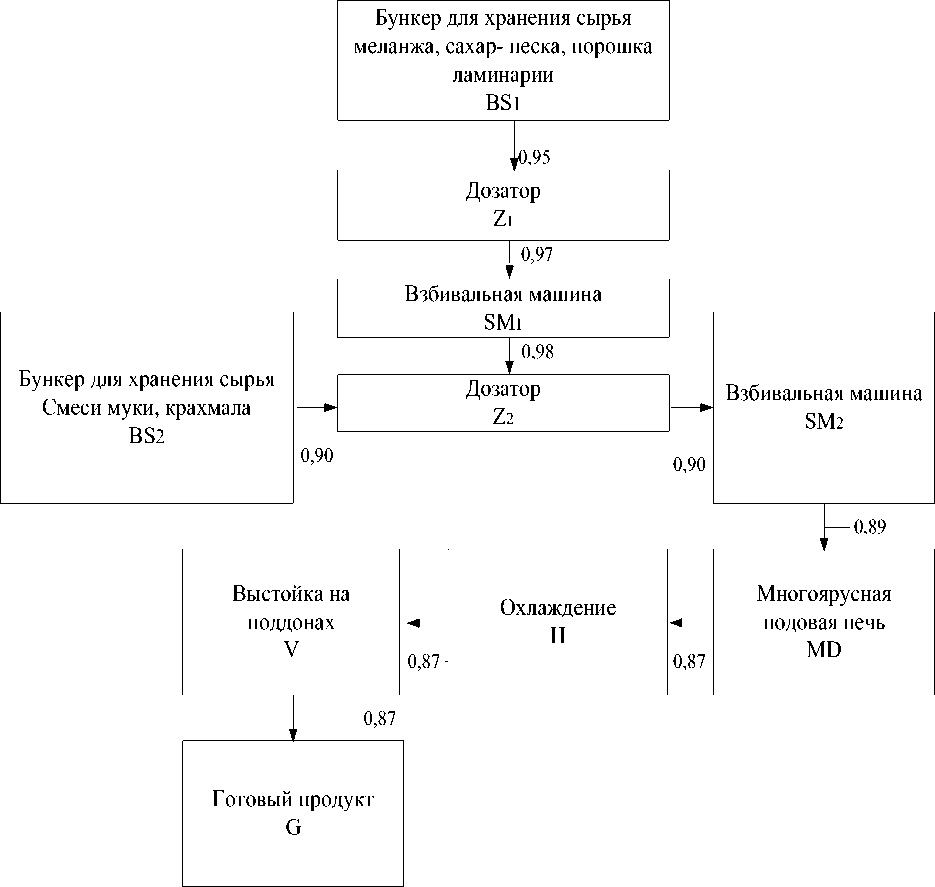
Принципиальная схема технологической системы

Интенсивность потоков сырья обозначена через Л = Л ХУ

Хλ У

По закону А.Н. Колмогорова изменение состояния каждого звена, с одной стороны, равно производной функции, с другой стороны, разности входных и выходных потоков. Общая модель функционирования технологической системы представляется системой дифференциальных уравнений:

¹ = A z ' B ( t ) - А ’ Z | ( t ) , BZ ₁               Z ₁ SM ₁     1

dSM

А’

dt dZ2

= ^A BSZ dt

'Z,SM, ■ ^Z 1 ^{( t} )   ^A SM,Z₂ ■ ^SM 1 ^{( t} ) ,

■ 2 ■ BS ⁽ t ) + A sm 1 z 2 ■ ^SM 1 ^{( t} )   ^A z 2 sm 2 ■ ^Z 2 ^{( t} ) ,

dSM

----= Л

dt dMP dt

'Z 2 SM 2 ■ ^Z 2 ^{( t} )   ^A SM 2 MP ■ ^SM 2 ^{( t} ) ,

" = ^A sm ₂ mp ■ ^SM 2 ^{( t} ) ^A mph ’ ^{MP ( t} ) ,

~7~ = ^A mph ’^{MP (t} ) - ^A hv ’ ^H(t ) , dt

~7~ = Ahv ' H(t) - Avg ’ V(t), dt dG = Avg • V (t) -dt

Учитывая, что масса сырья находящегося в технологических звеньях в настоящий момент времени t=0 от начала функционирования равно нулю, поставлены начальные условия:

/ (0) = 0; SM /0) = 0; Z2 (o)= 0; SM 2(o) = 0; MP (0 )= 0; H (o)= 0; V (0 )= 0; G (o) = 0

Для учета производительности звеньев и планируемых потерь сырья задаем интенсивности потоков сырья между звеньями, т.е. интенсивности технологических процессов в системе:

A bz 1 = 0,95 , A z 1 SM 1 = 0,97 , A sm i z 2 = 0,98 , A bsz 2 = 0,90 , A z 2 SM 2 = 0,90 ,

Asm2mp = 0,90,  Amph = 0,89, Amph = 0,89,  A^ = 0,87, AVG = 0,87

.

£n<.

Заданием входные потоки при случайных возмущениях в системе ^{Е в} и ^BS учтены:

B (t ) = 1,2796 + Ев (t),(11)

BS (t ) = 0,9800 + е stt)-(12)

Таким образом, задача Коши для (1)–(8) и (9) поставлена корректно [5]. Коэффициенты являются аналитическими функциями. Следовательно, в наблюдаемой области t ∈ (0;24) ч. существует аналитическое решение, которое было найдено в среде Maple, т.е. масса сырья спрогнозирована в звене в момент времени t. Например:

дозатор-1

60781    60781

( t ) = 48500  3940900

cos(73 1 ) 73 +

5895757 394090000

sin( 3 t )

(  97 t А

7 Ж И 60781  60781  3А

1 48500 + 3940900 J взбивальная машина-1

8683   229934523

⁽ t ) = 7000  31215080720

(  97 t А                                            (  49 t A я W )( 60781   60781 JI A I— 5i] J( 842251   5895757 JI A e      | 48500   3940900 J e      | 7000     3960400 J

Рассмотрим приближенное решение задачи (1)–(9), важное для практической оценки результатов по временному параметру t, полученное разложением решения в окрестности точки t=0 с точностью 0(t6) в ряд Тейлора. Например:

дозатор-1

60781    ( 60781 Д 5895757 A 2   (   5895757 -Д 571888429 А 3

• ⁽ t ) = 50000 t ⁺ ^ 2000000   10000000 J t + ^   600000000   ⁺ 3000000000 ^J t ⁺

  (   1251541571 JT    55473177613 А 4

^   240000000000    1200000000000 J t

121399532387  3     5380898228461

7 120000000000000   600000000000000 J t ^O( t )

взбивальная машина-1

• - 5895757   ₂  (_ 76644841   5895757 73 А ₃

S ⁽ t ) = 10000000 t ⁺ ^ 200000000 ⁺ 600000000 ^J t ⁺

(   76644841 /3   168141093883 А ₄

¹   16000000000 ⁺ 1200000000000 J t ⁺

(    8731616117 71    1457248361933 А _{5     6}

I 120000000000000   40000000000000 ^{J t +  (} t ) ^,0

.

Методом Рунге-Кутты численного решения задачи Коши использован для вычислительного эксперимента с моделью на временном промежутке t ^е [ ^{0; 10} ] ч с шагом 2 ч. Например, при t=2 получаем оценку:

Z1( t ) = 1.09755792278963792   SM1( t ) = 0.743520435131913127

G( t ) = 0.0138659198889257048

Например, при t=4 получаем оценку:

Z1( t ) = 1.21553600737581569   SM1( t ) = 1.10488653350408472

G( t ) = 0.338004342450588580

В момент времени t=6 получаем оценку:

Z1( t ) = 1.25241275371282136  . SM1( t ) = 1.23005032013201299  .

G( t ) = 1.59787170584128278

При достижении t=8 получаем:

Z1( t ) = 1.25966614448272042 SM1( t ) = 1.22507086651151464

G( t ) = 4.00643527064463711

.

Для момента времени t=10 спрогнозированы значения:

Z1( t ) = 1.23707865670857054 SM1( t ) = 1.24686931682856850

G( t ) = 7.31144311033594452

Взбивальная машина используется для замеса бисквитного теста. Без этой операции получение готового продукта невозможно. Поэтому звено SM 1 является лимитирующим звеном.

Переходные процессы завершаются соответственно через 6 и 10 ч. Часто взбивальная машина дополняет кондитерское и хлебопекарное оборудование, например тестомес, находит основное применение в кондитерской и хлебопекарной промышленности, служит при замешивании теста для разных видов кондитерского теста и простого, начинок для кондитерских изделий, глазурей, джемов, приготовления эмульсии при производстве печенья. Взбивальная машина с успехом используется во многих областях пищевой промышленности. Эти машины находят применение в кондитерской промышленности, где служат для замешивания теста.

Для определения нормального режима функционирования технологической линии, решаем систему линейных алгебраических уравнений, соответствующих дифференциальным уравнениям (1)-7):

ABZ 1 ■ B(t) AZ 1 SM 1 ■ Z1(t) = 0 ,

41 SM 1 ■ Z1(t)-Asm 1Z2 ■ SM^t) = 0 ,(14)

Absz2 ■ BS(t) + Asm 1 z2 ■ SM1 (t) — 42sm2 ■ Z2 (t ) = 0,(15)

AZ2SM2 ■ Z2(t)— ASM2MP ■ SM2(t) = 0 ,

ASMMP ■ SM2 (t) — AMPH ■ MP(t) = 0 ,

Amph ■ MP(t)—Ahv ■ H(t) = 0,(18)

АНр ■ H (t)—Avg ■ V (t ) = 0,(19)

И далее из уравнений (13)–(19) методом Жордана в общем виде получаем финальные состояния звеньев:

дозатор-1

Z1( t ) =

^ BZ1 b( t ) -

^Л Z1SM1

взбивальная машина-1

SM1( t ) =

^ bzi B( t )

^Л SM1Z2

дозатор-2

x _ ^ BSZ2 BS⁽ t ) ⁺ ^ BZ1 ^B( t )

^Z2( t ) =          j

^Л Z2SM2

;

взбивальная машина-2

45 ^bsc t ) +4z Л t )

SM2( t ) =    — ---- BZ¹

Л SM2MP многоярусная подовая печь hsz2 BS) t) + kBZ7b( t)

MP( t ) = -SZ^------—---

^ MPH охлаждение hsZ2VS) t) + kBZ7B( t) BSZ2          BZ 1

^H( t ) = 1-------------

^HV выстойка xBSZ2BS) t) + XBZ7B) t)

V) t ) =

BSZ2           BZ 1

^ VG

При подстановке конкретных значений интенсивности получаем численную оценку финальных состояний.

Заключение. Изделия с добавлением порошка из бурой водоросли ламинарии имеют пониженную энергетическую и повышенную биологическую ценность, на основании чего можно сделать вывод, что новые виды изделий относятся к кондитерским продуктам функционального назначения. Рентабельность разработанного ассортимента составляет 23 %. Поэтому выпуск данной продукции с использованием полуфабрикатов из нетрадиционного сырья возможен для расширения ассортимента, увеличения выработки изделий и применения их в питании человека.

Разработанная информационно-логическая модель технологической системы может быть использования для расчета выхода готовой продукции бисквитного полуфабриката с добавлением порошка ламинарии исходя из заданных объёмов сырья и режимных параметров.