Использование отражений от подстилающей поверхности для формирования произвольной поляризации при высокой направленности излучения в фазированных антенных решетках с управляемой поляризацией

-                     ,

4 я

где g(u) - весовая функция; d Q = sin O d O d ф ; F ( и ) - ДН по мощности в направлении орта.

При задании весовой функции, всюду равной единице, за исключением определенных направлений и угловых секторов, где она выбирается достаточно большой, максимум х практически совпадает с коэффициентом направленного действия (к. н. д.) решетки, а в диаграмме направленности (ДН) формируются глубокие «нули» или провалы в направлениях с g(u) >>1 .

В данной статье рассмотрена задача максимизации к. н. д. ФАР с УПП при ограничении на поляризацию излучаемого в направлении главного максимума поля и формировании глубоких «нулей» в ДН в заданных направлениях.

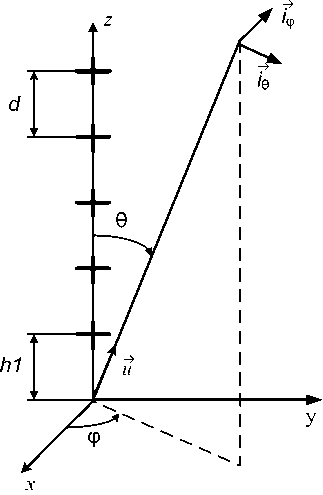
В качестве антенной решетки с управляемой поляризацией поля рассмотрим (рис. 1) вер -тикальную линейную антенную решетку, состоящую из N крестообразных (горизонтальных и вертикальных) элементарных вибраторов, в каждом из которых можно изменять амплитуды и фазы питающих токов. Крестообразные излучатели расположены эквидистантно с шагом d . Будем полагать, что решетка располагается на высоте h 1 над плоской идеально проводящей поверхностью.

Векторная комплексная ДН вертикальной решетки из горизонтально и вертикально ориентированных относительно поверхности земли излучателей в направлении орта и (0,ф), с учетом плоской идеально проводящей земли (коэффициенты отражения Френеля соответственно для вертикальной R _в и горизонтальной R _г поляризаций R _в = + 1, R _г= - 1), определяется выражением [1]

F ⁽ u ) = i e F ⁽ u ) ₊ i ф F ⁽ u ) =

N

= i e X [ y n j cos ^e sin Ф ^sin( kh n cos ^{e) +} z n ^{( - 1) sin e cos(} kh n ^{cos e)] +}                 (2)

n = 1

N

⁺ i ф X [ y n j cos ф ^sin( kh n cos ^e)]

или в матричной форме записи

F (u) = i e ( a H y + b ^H z ) + i ф ( a H y ) = i e e ^H v + i _T e H v ,

где v=

y

z

– 2 N -мерный вектор-столбец из амплитудно-фазовых распределений: y_n – в гори-

зонтально, а zn – в вертикально ориентированных относительно поверхности земли излучате- лей, (n= 1, N);

a=| I- j cos0sinфsin( kh n cos 0)11, a l=|h ^j cos^sinC kh n co ^s0)|| , Ь=| |^-s i ^{n0cos (} kh n c^os0)|| -

N -мерные векторы-столбцы; e =

– 2 N -мерные векторы-столбцы;

k = 2пГк - волновое число (к - длина волны); h = h + ( n -1) d , h 1 - высота подвеса первого из- n 1

лучателя над подстилающей поверхностью, d – шаг решетки; значок H означает операцию эр-митового сопряжения.

Для получения, в частности, круговой поляризации поля антенной решетки в направлении u (θ ,φ ) необходимо, чтобы в точке наблюдения с учетом отражений от подстилающей поверхности амплитуды ортогональных компонентов поля (F(u0) и Fθ (u0)) были φ равны и сдвиг по фазе между ними был равен π / 2, т. е. чтобы фазор поля в точке наблюдения

F _φ ( u 0 ) p = 2,,-. = ± j ,

F _θ( u 0 )

где знаки «+» и «–» определяются направлением вращения плоскости поляризации.

В вертикальной плоскости (φ = 0) ДН F(u0) определяется только токами zn вертикально θ ориентированных относительно поверхности земли излучателей и фазор поля антенной решетки в направлении θ = θ0, φ = 0 при круговой поляризации определяется следующим выражением:

£ Уп sin(khn cos 00 )

«=1_____________________________

£Zn sin00 cos(khn cos00) n или в матричном виде (учитывая (3) и (4))

±1 = a H ( e 0 ) y b ^H( θ 0 ) z

.

Как следует из последнего соотношения, для получения круговой поляризации поля решетки в направлении 0 = 0 0 (ф ₀ = 0) достаточно изменять пространственный период распределения отношения амплитуд и разности фаз токов с дискретом 180° в горизонтально и вертикально ориентированных относительно поверхности земли излучателях.

Для получения при этом высокой направленности луча при сканировании амплитуднофазовые распределения токов в горизонтально и вертикально ориентированных относительно поверхности земли излучателях должны выбираться исходя из обеспечения максимального значения к. н. д.

D =

2 4 π F ( u ₀ )

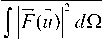
4π

где F ( и ) - ДН по мощности, d^ = sin O d O d ф ;

точку наблюдения.

u ₀ – орт, определяющий направление ( θ ₀ ,φ ₀ ) на

В матричной форме записи с учетом (3) соотношение (8) имеет вид

vHW v vHP v , где W=

a ( u ₀) a ^H( u ₀)+ a ₁ ( u ₀)a ₁^H( u ₀) b ( u 0 ) a ^H( u 0 )

a( u 0 )b ^H( u 0 )_; P ₌ B0

b ( u 0 ) b ^H( u 0 )       0C

– соответственно неотрицательно и

положительно определенные блочные эрмитовы матрицы размером 2 N ;

B = b mn ; С = c mn – квадратные матрицы размера N с элементами

b m. = -1 J ( aa H + _{a i} a H ) d a

4 π 4π

^C mn = 4^ I^{bb H d} “ .

b mn

Вычисляя интегралы (9) с учетом соотношений (4), получаем

1 [ sin y  sine cosy  siny  cos в  sine ]     _£[ siny   cosy  sine  cos в

41 y      в   + Y 2      Y 3 в 2   + в ^{3 J} , c mn = 21 y ³ y ^{2   +} в ³ в 2

2π2π где y = — ( n - m ) d ; P= — ( n + m λλ

1) d.

Максимум к. н. д. достигается на векторе амплитудно-фазовых распределений v , опреде-

-1                    -1

ляемом [1] v o = P ^{e (} u 0 ^)+a P- ^e i (u 0 ), где ^a - скаляр. Учитывая, что V o

yo z0

0

C -1

, где

B-1 и C-1 – обратные матрицы, получаем, что вектор-столбцы амплитудно-фазовых распределе- ний токов в горизонтально и вертикально ориентированных относительно поверхности земли излучателях, обеспечивающие максимальный к. н. д в направлении θ = θ0, φ0 = 0, определяются следующими выражениями [1]:

y0 aBa1 (6°), z0 CH^).       H_„1 _

Подставляя (10) в (7), имеем ± ¹ = ct ^ ⁽⁶ ° ) B a (9 ° ) / b (9 ° ) C b (9 ° ) и, следовательно, для создания круговой поляризации поля решетки в вертикальной плоскости и обеспечения при этом максимального значения к. н. д. в направлении θ 0 скаляр α по абсолютной величине:

а = bH (6° )C-1b(6°) / a, (6° )B-1ai (6°),

H         -1              H-1

где b (0 ° ) C b (0 ° ) , a 1 (0 ° ) B a ₁ (0 ° ) - максимальные к.н.д. при вертикальной и горизонтальной поляризациях соответственно.

Последнее означает, что, поскольку условия формирования максимумов ДН (F0 (0) и F (0)) Ф на обеих поляризациях различны, для получения равенства амплитуд ортогональных компонент поля в точке наблюдения и высокой направленности луча необходимо амплитуды токов в горизонтально ориентированных излучателях изменять по отношению к амплитудам токов в вертикально ориентированных излучателях в α раз, где α определяется отношением максимальных к.н.д. при вертикальной и горизонтальной поляризациях.

Для получения в направлении θ 0 , φ 0 поляризации, отличной от круговой, в формуле (5) необходимо подставить заданное значение фазора. Для формирования «нулей»в заданных направлениях в ДН антенной решетки необходимо в формулы для расчета элементов матриц В и С вводить весовую функцию вида

M

g(u) = 1 + £qMu -ui), i=1

где 5( u - U i ) - дельта функция [1].

Для обращения матриц В и С в этом случае целесообразно использовать правило Дуайра [4].

Проведем анализ численных результатов. Предположим, для рассматриваемой решетки N = 7, d = 0,5λ, h 1 = 0,25λ, θ 0 = 80°, поляризация круговая.

Нормированное амплитудное распределение приведено в таблице.

Амплитуды токов в горизонтальных и вертикальных вибраторах рассчитывали с использованием соотношений (9)–(11). Амплитудное распределение токов в горизонтальных вибраторах, ^{как видно из} таблицы, повторяет функцию sin ( kh_n cos 9 ° ) , ( n = 1,7 ) . Нормировка токов во всех вибраторах произведена к максимальному значению тока (в третьем горизонтальном

Таблица

n 1 2 3 л 5 6 7 yn 0.27581 0.74395 1.00000 0.96069 0.65044 0.13855 –0.30368 zn 0.72450 0.53896 0.12119 –0.20026 –0.66059 –0.64673 –0.86146 вибраторе). Знак «+» или «–» соответствует фазе тока 0 или π и определяется, следователь- но, знаком «+» или «-» функции sin f 2^ hn cos 00

для горизонтальных вибраторов и функции

| 2n cos —h cos 00

I X "        0

для вертикальных вибраторов.

Соответствующие данному амплитудно-фазовому распределению токов в горизонтальных и вертикальных вибраторах ДН и поляризационная характеристика (зависимость коэффициента эллиптичности r от угла θ) представлены на рис. 2.

Как показывает анализ, при сканировании в вертикальной плоскости можно получать круговую поляризацию излучаемого поля в направлении главного лепестка при максимальном к.н.д. с использованием отраженных от поверхности земли волн. За счет интерференции прямого и отраженного лучей создается необходимая пространственная ориентация и фазовый сдвиг между ортогональными линейно-поляризованными волнами, дающими в сумме волну круговой поляризации. Для этого необходимо производить изменение пространственного периода распределения отношения амплитуд и разности фаз токов в горизонтально и вертикально ориентированных относительно поверхности земли излучателях вдоль вертикальной оси, при этом разность фаз токов в этих излучателях следует менять скачкообразно от 0 до π, а амплитуды токов в горизонтально ориентированных излучателях изменять по отношению к амплитудам токов в вертикально ориентированных излучателях во столько раз, во сколько максимальный к. н. д. при вертикальной поляризации отличается от максимального к. н. д. при

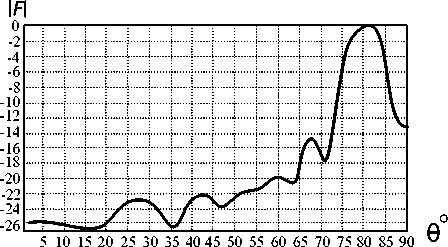
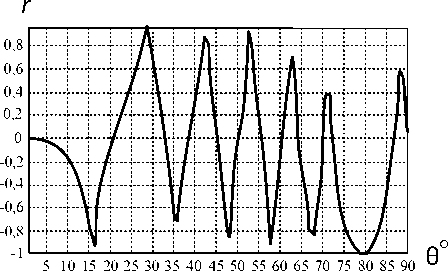
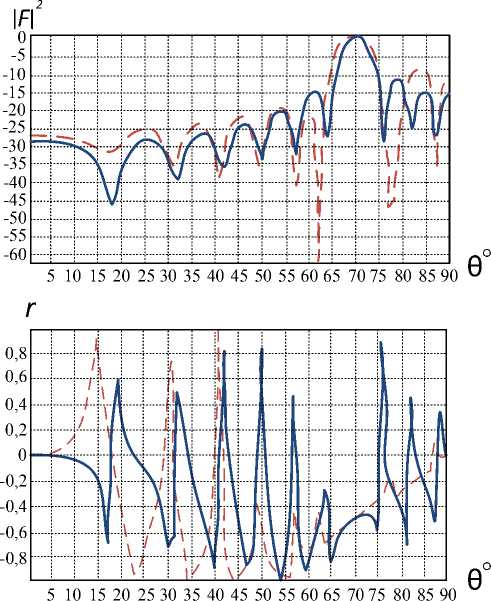
Рис. 3

горизонтальной поляризации, т. е. поляризация поля каждого излучателя антенной решетки линейная.

На рис. 3 приведены оптимальные диаграмма направленности и поляризационная характеристика для решетки N = 10, d = 0,5λ, h ₁ = 0,25λ, θ₀ = 70°, поляризация – эллиптическая с коэффициентом эллиптичности 0,5 без формирования «нулей» (сплошные кривые) и с формированием трех «нулей» в направлениях θ₁ = 62° (направление первого бокового лепестка слева), θ 2 = 77°, θ 3 = 78° (направление первого бокового лепестка справа) с весовыми коэффициентами q 1 = q 2 = q 3 = 10 (штриховые кривые).

Как видно из рис. 3, в направлении θ 0 = 70° коэффициент эллиптичности равен 0,5, в заданных направлениях сформировались «нули»: в направлении θ₁ = 62° – глубиной –60 дБ; в направлениях θ 2 = 77° и θ 3 = 78° – провал шириной на уровне –25дБ примерно равной 4° (четверти ширины ДН по половинной мощности). При этом наблюдается некоторое увеличение (на 2 дБ) уровня бокового лепестка справа, расширение ширины ДН (на 1°).

Выводы

• 1.    Можно получать круговую поляризацию излучаемого поля в направлении главного лепестка при максимальном к. н. д. с использованием отраженных от подстилающей поверхности волн. За счет интерференции прямого и отраженного лучей создаются необходимая пространственная ориентация и фазовый сдвиг между ортогональными линейно-поляризованными

• 2.    В процессе сканирования луча в вертикальной плоскости по результатам синтеза ФАР в направлении главного максимума формируется заданная поляризация при высокой направленности излучения, в заданных направлениях в ДН формируются «нули», т. е., подбирая значения весовых коэффициентов, можно изменять форму ДН.

волнами, дающими в сумме волну круговой поляризации. При этом поляризация поля каждого излучателя антенной решетки – линейная.

Using Reflections from a Padding Surface for Forming Arbitrary Polarization in Phased Antenna Arrays with Controlled Polarization Under High