Использование схем типа DRP высокого порядка аппроксимации и метода крупных вихрей с релаксационной фильтрацией для расчёта турбулентных течений газа на примере распада вихря Тейлора-Грина

В настоящее время в связи с ростом вычислительных ресурсов и необходимостью более точного моделирования течений газа в различных устройствах всё большую популярность приобретают методы высокого порядка аппроксимации. В качестве одного из подклассов данных методов можно выделить те, которые основаны на схемах с высокой разрешающей способностью, не только имеющих высокую точность описания решения, но и сохраняющих её для более широкого диапазона волновых чисел. Примерами таких схем служат компактно-разностные схемы и центрально-разностные схемы высокого порядка. Существуют также оптимизированные версии этих схем: DRP [1] и CDRP [2], где DRP означает Dispersion-Relation Preserving — сохраняющие дисперсионное соотношение. Изначально названные схемы предназначались для задач акустики, где зачастую нужно обеспечить максимально возможное разрешение волн различной длины на достаточно грубых сетках. В схемах типа DRP (при сохранении одного и того же

числа точек в шаблоне) их формальный порядок понижается, а волновые характеристики улучшаются. Такие схемы называют подобными спектральным (spectral-like).

Кроме применения к описанию распространения волн, схемы DRP могут быть использованы и для исследования турбулентных течений. При этом основной идеей является разрешение вихревых структур вплоть до самых мелких, доступных на имеющейся расчётной сетке. Так, к примеру, для 13-точечной оптимизированной схемы DRP 4-го порядка аппроксимации [1] пределом точности можно считать 3,36 точек на длину волны возмущения, что значительно меньше 32 точек, необходимых для стандартных схем 2-го порядка. Все возмущения, имеющие меньше точек на длину волны, чем требуется схемой, удаляются специальным узкополосным фильтром, слабо влияющим на крупные масштабы. Таким образом реализуется метод крупных вихрей. При этом вместо вихревой вязкости, которая зачастую явно присутствует в уравнении, диссипация энергии с мелких масштабов осуществляется фильтрацией. Этот подход называют методом крупных вихрей с релаксационной фильтрацией (LES-RF). Его также можно отнести к классу неявных методов крупных вихрей (ILES), в которых диссипация обеспечивается за счёт свойств самой схемы, а не модификацией решаемого уравнения.

Метод крупных вихрей с релаксационной фильтрацией имеет ряд преимуществ по сравнению с традиционным, использующим вихревую вязкость, — это отсутствие в нём каких-либо параметров (кроме силы фильтра), что ведёт к большей универсальности метода, сохранение величины эффективного числа Рейнольдса течения [3], а также простота в реализации.

Целью данной работы является исследование возможностей метода крупных вихрей с релаксационной фильтрацией на основе оптимизированных схем типа DRP при применении его для расчёта турбулентных течений, а также проведение анализа зависимости решения от силы фильтра и размера шага по времени. В качестве тестовой задачи рассматривается распад вихря Тейлора–Грина. Это течение, представленное Тейлором и Грином в 1937 году [4], широко изучено теоретически, поэтому многие авторы прибегают к нему для тестирования адекватности описания турбулентности различными методами. В частности, в работах [5, 6] обсуждаются спектральные методы, публикации [7, 8] посвящены неявным методам крупных вихрей, [9] — схеме КАБАРЕ, [10] — квазигидродинамическому подходу. В работе [11] задача решается с помощью центральных конечно-разностных схем высокого порядка аппроксимации. В [12] вихрь Тейлора–Грина рассчитывается псевдоспектральным и вихревым методами на подробных расчётных сетках. Кроме того, подобному течению посвящены публикации [13] и [14].

2.    Постановка задачи

Вихрь Тейлора–Грина представляет собой течение, определяемое в периодичной кубической расчётной области размерами -п L <  x, y, z < п L при следующих начальных условиях ( t = 0):

v • I x I     I У I     I z I u = Vn sin — cos — cos — ,

⁰ I L J    I L J    I L J

I x I I У I I z I v = - V , cos — sin — cos — , 1        0 I L J I L J I L J

w = 0,

P = P 0

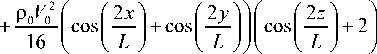
где V₀ — максимальная начальная скорость; p ₀ и p ₀ — средние начальные плотность и давление. Вихрь, определяемый условиями (1), является неустойчивым, в силу чего происходит его распад, и в некоторый момент времени течение становится турбулентным. Переход к турбулентности сопровождается уменьшением масштабов вихрей, находящихся в области, и диссипацией кинетической энергии.

В работе рассмотрены два случая течения с разными значениями числа Рейнольдса: Re = 1600 и Re = 3000. Числа Рейнольдса вычислялись по характерному размеру области L , максимальной начальной скорости V₀ , начальной плотности р ₀ и вязкости ц (в данном случае — постоянной). На рисунке 1 показана эволюция течения для Re = 3000. Видно, что изначально в расчётной области присутствуют только крупные вихри (Рис. 1 а ). Далее наблюдается их локальный распад на более мелкие структуры (Рис. 1 б ), и впоследствии происходит турбулизация всей области (Рис. 1 в ). Аналогичная картина имеет место и для числа Рейнольдса Re = 1600 .

Для расчётов применялся решатель, использующий «сжимаемые уравнения» Навье–Стокса (compressible N–S equations) с уравнением состояния совершенного газа. В обоих случаях число Маха М = V ,/ с ₀ , где с ₀ = Y p P ₀ /р₀ , равнялось 0,09 (здесь у — газовая постоянная: у = 1,4). Как известно, влияние сжимаемости среды на её течение для малых чисел Маха (M <  0,3) является слабым [5].

Рис. 1. Эволюция вихря Тейлора–Грина для

Re = 3000 ; структура течения соответствует моментам времени

t ^* :

0 ( а ), 9 ( б ), 20 ( в ); показаны положительные изоповерхности Q -критерия, раскрашенные z -компонентой вектора завихренности

Фактически максимальное отклонение плотности от среднего значения составило около 0,4% Таким образом, влияние сжимаемости на результаты в данной работе не принималось во внимание. Число Прандтля Pr = ц c p /к равнялось 0,71 (где к — коэффициент теплопроводности. В рассмотренном диапазоне чисел Рейнольдса наибольшая скорость диссипации энергии достигалась для безразмерного момента времени t* = V 0 t/L ® 9, при этом сам расчёт продолжался до t* = 20 .

3.    Уравнения и схемы 3.1.    Определяющие уравнения

В работе используются уравнения Навье–Стокса, записанные для совершенного газа в криволинейной системе координат в неконсервативной форме:

• ¹    J A x * ₊ A Э_{А +} A z £ W J A x с^ a 5п ₊ а z адШ J а x S^ а ^ a z d^d U = f v , (2) д t (   д x y д y д z J д^ ( д x y д y     д z J др ( д x y д y д z J dZ

где U = ( p uvw p ) T — вектор примитивных переменных (Т — символ операции транспонирования);

Z = Z(x, У, z), П = П(x, У, z), Z = Z(x, y, z) — расчётная система координат, введённая таким образом, что значения координат Z, П, Z

в узлах

структурированной расчётной сетки

совпадают со значениями

индексов ( i , j , k ) данных узлов;

F

v

( Y- 1)

A

x

^ и

Р 0 u 0

0 u 00

Y Р 0

0 0

0 u

0 ) V p и ,

, A y

^ v

. 0

0 v

Р

v

Y Р

0 0

0 v

0 )

V р 0

A z

Г w  00

0  w0

0  0

0  00

, 0  00

Р 0 ^

0 0

0   0

^{w 1} p Y Р w J

1 Г дт 5т дт ) xx ^y        zx

p(дx   дy    дz J дт дт дт

¹ xy + yy + zy

p( д x    д y    д z J

1 Г дт^    ^дт yz   5t_zz )

xz ^+     ^y ^+     zz

p(д x   д y    д z J

Гд ² T  д ² T  д ² T )     д и д v     д w     Гд v  д и )    Гд w  д и )     Гд w  д v )

^к1 “7Т ⁺ ТТ ⁺ ТТ 1 ^{+ т} xx 7Т ^{+ т} yy T" ^{+ т} zz "Т ^{+ т} xy I , ' , 1 ^{+ т} xz I "Т ⁺ "Т 1 ^{+ т} yz I     '

^д x   д y   д z J     д x   "оy     д z     ^д x  д y J    ^д x  д z J     ^д y  д z J

Здесь T = P /( p R ) — температура; R — индивидуальная газовая постоянная (в работе — газовая

„        , х dE dn dZ                                , постоянная воздуха: R = 287,1); —, —, —,... — метрические коэффициенты; тij — компоненты дx   дx   дx тензора вязких напряжений: ту = ц

'ги^/и' д x j   д x i

2 д и, —о. —-

3 j д x _k

, где u i = { и , v , w }, x i = { x , y , z }.

Использование неконсервативной постановки задачи обусловлено, прежде всего, её вычислительной сложностью. Алгоритмы расчётов для неконсервативного случая требуют меньшего объёма оперативной памяти вычислительной машины, а также имеют меньшее число операций, что ведет к общему ускорению расчётов. При этом в отсутствие разрывов решения неконсервативная и консервативная постановки эквивалентны.

• 3.2.    Схема DRP

Система уравнений (2), (3) решается методом конечных разностей со схемой DRP для расчёта производных по пространственным координатам (Е, n, Z) ■ Эта схема представляет собой

N оптимизированную центрально-разностную схему следующего вида: (д U/дЕ) ikk «^ am (Ui+m, k, k - Ui - m, k, k), m =1

где ( д UJ <3E)^ _k — производная искомой функции по E в точке расчётной сетки с индексами ( j , j , k ) , при этом N = ( N full - 1 ) /2, где N full — количество точек схемы по одному индексному направлению, a _m — коэффициенты схемы. В данном случае считается, что сетка в расчётной системе координат равномерна и имеет единичный шаг, то есть AE = 1 (что справедливо в силу того, что расчётная система координат, по сути, представляет собой индексы ячеек сетки). Аналогично можно записать и производные по остальным двум координатам расчётной системы ( n и Z )■ Коэффициенты a m схемы определяются исходя из двух условий: первое — это необходимость аппроксимации производной с нужным порядком точности, второе — минимальность дисперсионной ошибки, то есть разности между аналитическим ( k ) и численным ( k ^* ) волновыми числами.

Связь волновых чисел для центрально-разностной аппроксимации можно записать как

N k *Ax = 2^ am sin (mkAx).

m =1

С использованием (4) условие минимизации относительной разности безразмерных волновых чисел k * A x и k A x представляется в следующем виде:

2 2 k A x - k A x           ‘ny, *         ,

E =[  ---------- '-d ( k A x ) = f k A x - k A x\d (ln( k A x )) ^ min,

J      kAx                  ,                   1

П 1                                                ln(4 1 )

где n 1 , n ₂ — границы диапазона волновых чисел, для которых производится оптимизация. В качестве значения n 1 авторами [1] принималось число л/ 16 (для любых схем), n ₂ выбиралось равным п/ 2 для 9- и 11-точечных схем (DRP4 и DRP5) и 3п/5 для 13-точечной схемы (DRP6).

Во всех трёх схемах первые два коэффициента a _m обусловливались аппроксимацией производной, что давало формальный 4-й порядок аппроксимации. Остальные коэффициенты определялись из условия (5). Коэффициенты рассматриваемых схем представлены в таблице 1.

Таблица 1. Коэффициенты различных схем DRP 4-го порядка

	DRP4	DRP5	DRP6
a 1	0,841570125482	0,872756993962	0,907646591371
a 2	-0,244678931765	-0,286511173973	-0,337048393268
a 3	0,059463584768	0,090320001280	0,133442885327
a 4	-0,007650904064	-0,020779405824	-0,045246480208
a 5	–	0,002484594688	0,011169294114
a 6	–	–	-0,001456501759

Предельное разрешаемое схемами количество точек на длину волны составляло 4,22, 3,93 и 3,36 для DRP4, DRP5 и DRP6 соответственно. Для расчётов в данной работе из представленных трёх схем была выбрана схема DRP6, имеющая наилучшие волновые характеристики и, кроме того, приемлемую вычислительную сложность.

• 3.3.    Фильтрация решения

Для обеспечения устойчивости схемы DRP и диссипации энергии мелких масштабов применяются оптимизированные селективные фильтры вида:

Г        N                 х)

U. -, — U ■ , — ст ddJ - / + d (и -; "VU.

• i ,    j , k i , j , k I 0 i , j , k / j m. \ i + m , j , k i - m , j , kJ I , k             m =1                            )

где U_jk и U_ljk — фильтрованная по £ координате расчётной системы функция в точке сетки с индексами ( i,j,k ) и её начальное (до фильтрации) значение в той же точке; сте [ 0,1] — сила фильтра; d m — коэффициенты фильтра. Фильтрация по п и Z записывается аналогично.

Коэффициенты d_m определяются путём минимизации следующего функционала:

^1п(П 2 )

j D_id ( k A x ) d ( ln( k N x ) ) ^ min,

^ln(n i )

где D_id ( k A x ) — идеальная демпфирующая кривая в пространстве волновых чисел, равная нулю при k A x = 0 (то есть не модифицирующая хорошо разрешённые схемой волны) и единице при k A x = п (то есть полностью подавляющая высокочастотные волны, плохо разрешённые схемой). В качестве такой кривой авторами [1] использовалась следующая функция:

^Dd ( ^{k N} ) =

e

1п(2)Г k N x -^ k 0,2п

Границы интегрирования р 1 и п ₂ в (6) для 9-, 11- и 13-точечных фильтров выбирались такими же, как и для соответствующих 9-, 11- и 13-точечных схем DRP. Коэффициенты фильтров, полученные с помощью (6) и (7), представлены в таблице 2. Фильтрация проводилась в конце каждого шага по времени последовательно по координатам расчётной системы ^ , п и Z ■

Таблица 2. Коэффициенты оптимизированных фильтров для схем DRP

	SFO4	SFO5	SFO6
d 0	0,24352749312	0,215044884112	0,190899511506
d 1	-0,20478888064	-0,187772883589	-0,171503832236
d 2	0,12000759168	0,123755948787	0,123632891797
d 3	-0,04521111936	-0,059227575576	-0,069975429105
d 4	0,00822866176	0,018721609157	0,029662754736
d 5	–	-0,002999540835	-0,008520738659
d 6	–	–	0,001254597714

• 3.4.    Схема LDDRK

Для интегрирования по времени применялась оптимизированная схема Рунге–Кутты 4-го порядка LDDRK (Low Dispersion and Dissipation Runge–Kutta) [15], содержащая два слоя переменных: основной ( U ) и промежуточный ( V ). Оптимизация этой схемы основывалась на том же принципе, что и оптимизация схемы DRP, а именно путём минимизации дисперсионных ошибок улучшались её волновые свойства. Переход на новый шаг по времени в схеме LDDRK осуществляется с помощью шести последовательных подшагов (в отличие от 4-х для стандартной схемы RK4). При этом на каждом из подшагов j с помощью схемы DRP вычисляется невязка Rj (U), представляющая собой все слагаемые в (2) (кроме dUptt), перенесённые в правую часть. Данную схему можно записать в следующем виде:

V j =a V j-i + А tR j ( U j-1 ) , U j = U j-i

^       ( j = 1,..., 5 ),

где в фигурных скобках указана последовательность одного подшага j . Сначала с помощью невязки R j ( U j 1 ) , коэффициента a j и значения V j 1 переменных промежуточного слоя с предыдущего шага рассчитываются соответствующие переменные V _j промежуточного слоя на текущем подшаге. Далее с учётом коэффициента в j осуществляется пересчёт полей основного слоя U j . При j = 1 под величиной U 0 подразумевается переменная U j 1 до начала интегрирования на очередном подшаге по времени. Значение 5 определяет количество подшагов. Коэффициенты a j и в j используемой схемы представлены в таблице 3.

Таблица 3. Коэффициенты оптимизированной 6-шаговой схемы Рунге–Кутты 4-го порядка

j	a j	р j
1	0,0	0,032918605146
2	-0,737101392796	0,823256998200
3	-1,634740794341	0,381530948900
4	-0,744739003780	0,200092213184
5	-1,469897351522	1,718581042715
6	-2,813971388035	0,27

4.    Результаты

Как сказано ранее, расчёты проводились для двух значений числа Рейнольдса: Re = 1600 и Re = 3000 . При этом применялись равномерные расчётные сетки размерностью 64³, 128³ и 256³ ячеек. Также исследовалось влияние силы фильтра на получаемые результаты. Необходимо отметить, что для успешного применения описанных схем в расчётах турбулентных течений требовалась минимальность данного влияния. Расчёт (если обратное не оговаривалось) проводился с шагом по времени, выбранным из следующего условия для числа Куранта: CFL ® 0,45.

Как известно, для прямого численного моделирования течения расчётная область (при решении спектральными методами) должна содержать не менее Re ⁹⁴ ячеек [16], что соответствует сетке с числом ячеек 253 3 в случае Re = 1600 и числом ячеек 406³ в случае Re = 3000. Исходя из этого, расчёт для Re = 1600 с сеткой 256³ является прямым численным моделированием. Однако следует учитывать и разрешающую способность используемой схемы: поскольку точность решения значительно ухудшается для самых высоких волновых чисел, эффективное сеточное разрешение для мелких структур становится меньше. Таким образом, любой из описанных случаев может рассматриваться и как относящийся к методу крупных вихрей.

Сравнение результатов проводилось по профилю безразмерной скорости диссипации кинетической энергии £ . Величина £ находилась из следующего соотношения: £ = - dEjdt* , где E k — кинетическая энергия в расчётной области -п L <  x , y , z < п L объёмом Q , определяемая из следующего соотношения:

E k =

1 г U ² + V ² + W ²

РЩ^Р   2

d Q .

• 4.1.    Случай Re = 1600

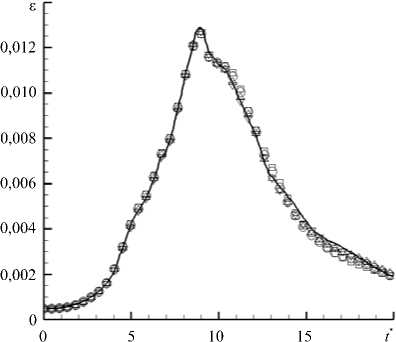
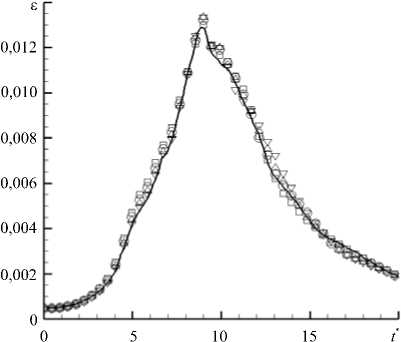
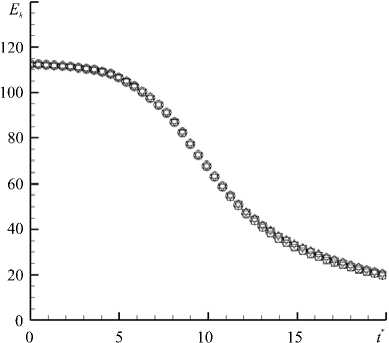
На рисунке 2 представлены результаты расчётов для различных сеток и силы фильтра. Для сравнения приведены данные прямого численного моделирования, взятые из работы [12], полученные с помощью псевдоспектрального метода на сетке размерностью 5123 ячеек. Из рисунка видно, что в случае сетки размерностью 2563 ячеек наблюдается почти полное совпадение результатов схемы DRP и спектральной схемы, а также минимальная зависимость результатов схемы DRP от силы фильтра. Последнее можно объяснить тем, что наибольший вклад в решение (при разрешении мелких масштабов) вносит молекулярная вязкость, а вклад фильтрации заметно уменьшается. Также можно отметить неплохую разрешающую способность схемы: вплоть до безразмерного момента времени порядка t* ® 13 расхождение со спектральным решением минимально. Данное обстоятельство говорит и о том, что до этого момента размер основных несущих энергию вихрей остаётся достаточно большим. Основное расхождение для сетки из 2563 ячеек связано с диссипацией энергии мелких вихревых структур, заполняющих область ближе к концу расчёта. На сетке размерностью 1283 ячеек результаты расчётов с разной силой фильтра несколько расходятся, а на сетке из 643 ячеек отличие становится ещё более заметным, оставаясь, тем не менее, небольшим. Прослеживается, что с уменьшением размерности сетки диссипация энергии на ранних этапах возрастает, что вызвано неудовлетворительным разрешением вихревых структур и усилением влияния фильтрации. При этом вплоть до сетки в 643 ячеек пик скорости диссипации энергии сохраняет форму и амплитуду, хотя и «раздваивается» с ростом значения силы фильтра (Рис. 2в). На сетке в 323 ячеек, приведённой для сравнения, видно, что пик скорости диссипации сильно сдвинут влево, и следовательно, диссипация происходит раньше и на более крупных масштабах, поскольку мелкие масштабы на этой сетке отсутствуют. В то же время амплитуда пика сохраняется довольно хорошо.

а

б

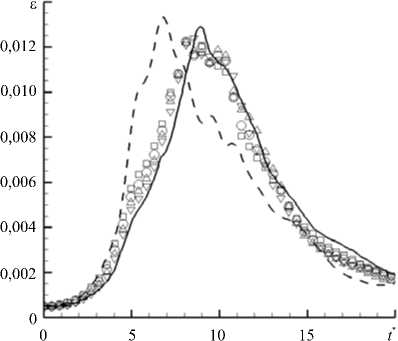
Рис. 2. Результаты расчётов для Re = 1600: безразмерная скорость диссипации кинетической энергии е согласно псевдоспектральному методу [12] (сплошная линия) и для схемы DRP при расчётных сетках размерностью 256³ ( а ), 128³ ( б ) и 64³ ( в ) ячеек, а также кинетическая энергия E_k ( г ) при сетке размерностью 256³ ячеек, полученные с учётом разной силы фильтра (символьные обозначения); сила фильтра составляет: о = 0,2 ( V ), о = 0,4 ( △ ), о = 0,6 ( О ), о = 0,9 (□); на части ( в ) штриховой линией показан характер е при сетке размерностью 32 3 и силе фильтра о = 0,2

в

г

• 4.2.    Случай Re = 3000

Случаю Re = 3000 посвящена работа [7], в которой также рассматривается метод крупных вихрей с релаксационной фильтрацией, но основывается он на стандартных центрально-разностных схемах. При этом авторы [7] предполагают, что размер сетки 256³ недостаточен для точного описания решения (это также вытекает из необходимого количества ячеек Re ⁹⁴ ), поэтому он будет использован только для относительного сравнения результатов для различных разрешений сетки.

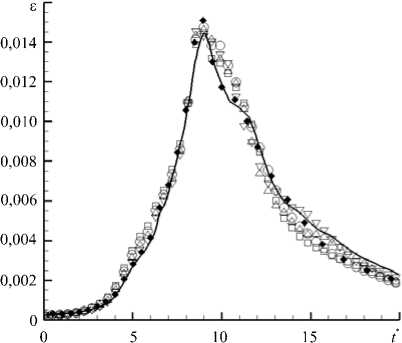
Результаты расчётов для Re = 3000 представлены на рисунке 3. Для сравнения используются результаты прямого численного моделирования, полученные псевдоспектральным методом на сетках размерностью 256³ [5] и 384³ [11] ячеек. Как видно из рисунка, уже на сетке в 256³ ячеек решение начинает зависеть от силы фильтра. Для фильтров с силой а >  0,2 пик скорости диссипации в момент времени t * ® 9 уменьшается по амплитуде и «размазывается» на более поздние моменты времени 10 <  t * <  12. Аналогичное явление наблюдается и на сетке в 128³ ячеек, только в этом случае для фильтров с силой о 0,2 амплитуда пика увеличивается, и диссипация в целом осуществляется несколько раньше, что приводит к её заметному снижению при 12 <  t * <  18. Для фильтров же с силой ст = 0,2 полученные результаты довольно хорошо ложатся в диапазон псевдоспектральных (в частности, по положению и амплитуде пика) как для сетки размерностью 256³, так и для сетки в 128³ ячеек.

Следует отметить, что поведение представленных результатов для сеток в 256³ и 128³ ячеек напоминает поведение результатов, вычисленных псевдоспектральными методами на сетках в 384³ и 256³ ячеек: на более грубой сетке амплитуда пика скорости диссипации становится больше. При сетках в 64³ и 32 3 ячеек ситуация похожа на ту, что имела место для Re = 1600, но при Re = 3000 диссипация энергии происходит в более ранние моменты времени в силу недостаточного разрешения мелких вихревых структур.

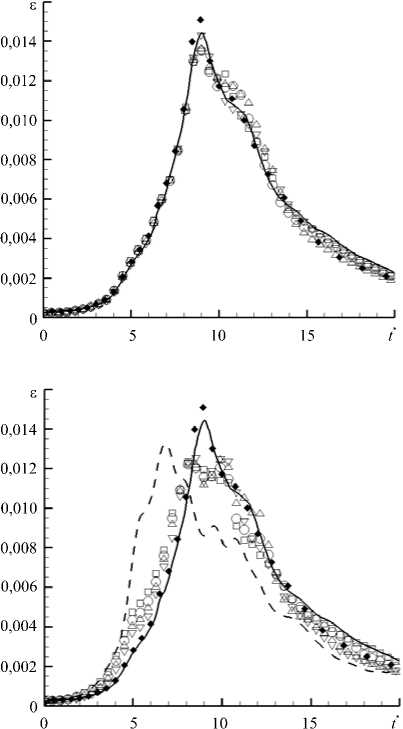
Рис. 3. Результаты расчётов для Re = 3000 : безразмерная скорость диссипации кинетической энергии £ для псевдоспектральной схемы на сетках из 384³ [11] (сплошная линия), 256³ [5] (символы ♦ ) ячеек и схемы DRP на сетках 256³ ( а ), 128³ ( б ) и 64³ ( в ) ячеек, а также кинетическая энергия E_k ( г ) при сетке размерностью 256³ ячеек, полученные с учётом разной силы фильтра (символьные обозначения); сила фильтра составляет: а = 0,2 ( ▽ ), а = 0,4 ( △ ), а = 0,6 (О), а = 0,9 (□); на части ( в ) штриховой линией показан характер £ при сетке размерностью 323 и силе фильтра а = 0,2

а

б

в                                                       г

о1-----------1----—----1----—----1-----------1

0           5          10          15           f

• 4.3.    Зависимость решения от размера шага по времени

Результаты, описанные ранее, были получены при размере шага по времени, определённом согласно условию CFL ® 0,45. При этом зависимость результатов от силы фильтра (в выбранном

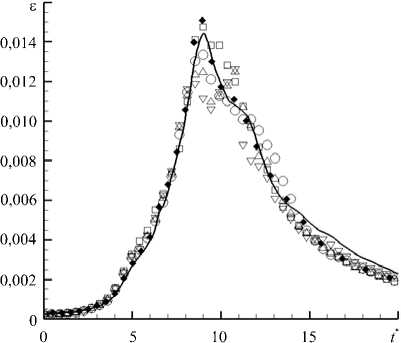
Рис. 4. Результаты расчётов для Re = 3000 зависимости от времени безразмерной скорости диссипации кинетической энергии ε при спектральной схеме на сетке 384³ (сплошная линия) и 256³ (♦) ячеек и схеме DRP с расчётной сеткой размерностью 128³ ячеек и силой фильтра σ= 0,6 с разным временным шагом, то есть при

CFL « 0,06 ( ▽ ), CFL « 0,1 ( △ ), CFL « 0,23 ( O ), CFL « 0,45 (□)

диапазоне 0,2 ≤σ≤ 0,9 ) была минимальной. «Общий объём» фильтрации χ за некоторое время t можно выразить как

χ =σ⋅ n ,                  (8)

где n = t ∆ t — количество шагов за время t , ∆ t — размер шага по времени [11]. Таким образом, при уменьшении ∆ t значение χ будет увеличиваться, и общая диссипация в области за тот же отрезок времени будет больше, что может повлиять на решение.

Рассмотрим случай Re = 3000 и проведём расчёты скорости диссипации кинетической энергии ε с фиксированной силой фильтра σ= 0,6 на сетке в 128³ ячеек при нескольких условиях для числа Куранта: CFL ≈ (0,06; 0,11; 0,23; 0,45) , то есть с разными величинами шага по времени. Полученные результаты представлены на рисунке 4.

Как видно из рисунка, результаты зависят от числа Куранта и отличаются друг от друга достаточно сильно, и разница проявляется (Рис 3б). Это объясняется тем, что при значительно сильнее, чем в случае изменения силы фильтра σ

изменении величины шага по времени в m раз (в данном примере m = 7,5 ), общая диссипация за счёт фильтра будет отличаться также в m раз. К примеру, расчёт с CFL = 0,2 и σ=0,5 эквивалентен, с точки зрения объёма фильтрации (8), расчёту при CFL = 0,4 и σ=1,0 , поскольку уменьшается эффективное разрешение схемы, что и делает результаты похожими. Таким образом, значение искомой величины в каждой конкретной ячейке области существенно зависит от числа Куранта в этой ячейке. Так, если бы в данной задаче использовалась неравномерная сетка с уменьшенным в несколько раз размером всего одной ячейки, результаты для всей области поменялись бы, как на рисунке 4, в силу того, что шаг по времени из условия Куранта также бы уменьшился. Аналогичное явление характерно для большинства практических задач, в которых сетка может быть сильно неравномерной и иметь вариации размеров ячеек в десятки, сотни и более раз.

В действительности это говорит о том, что используемая схема (по крайней мере, в задачах, похожих на рассмотренную здесь) не обеспечивает сходимость решения по времени. Однако, несмотря на это, данные схемы применяются в практических расчётах с достаточно хорошими результатами [3].

5.    Заключение

Проведено исследование свойств метода крупных вихрей с релаксационной фильтрацией при реализации с помощью схем типа DRP применительно к моделированию турбулентных течений. С его помощью осуществлены расчёты распада вихря Тейлора–Грина. Вычислительные эксперименты для различных расчётных сеток и чисел Рейнольдса показали хорошее совпадение с данными спектральных расчётов других авторов. Оценено влияние единственного свободного параметра рассмотренной схемы DRP — силы фильтра. Обнаружено, что сила фильтра влияет на решение в меньшей степени при использовании подробной расчётной сетки, разрешающей довольно мелкие вихри. При этом на более грубых сетках, где зависимость результатов непосредственно от молекулярной вязкости меньше, сила фильтра проявляет несколько большее влияние. Тем не менее, при фиксированном размере шага по времени это влияние достаточно мало.

В работе также выявлена важная особенность метода крупных вихрей с релаксационной фильтрацией — это существенная зависимость решения от размера шага по времени (при фиксированной силе фильтра), которая фактически означает отсутствие его сходимости по времени. Эту особенность можно объяснить тем, что уменьшение размера шага по времени (при условии фиксированной силы фильтра) приводит к увеличению общей диссипации за счёт фильтрации и дополнительному «размазыванию» решения. Это в свою очередь может сказаться на результатах решения при использовании неравномерных сеток, которые зачастую применяются на практике. Примерами могут служить исследования любых течений, ограниченных стенками, где обычно прибегают к сгущению расчётной сетки по направлению к стенке. По мере уменьшения размера пристеночных ячеек изменяется и допустимый размер шага по времени, что может привести к другим результатам.

Тем не менее, несмотря на эту особенность, данная схема успешно применяется в сложных задачах (см., например, расчёт шума турбулентных струй в [3]). Кроме того, возможна доработка рассмотренного метода крупных вихрей с релаксационной фильтрацией, например, с помощью дополнительного управления силой фильтра.