Использование симметрии графиков функций при решении систем уравнений

Углубленное изучение математики в школе предусматривает помимо получения учащимися расширенного объема знаний и техники владения предметом формирование у них устойчивого интереса к предмету, выявление и развитие математических способностей, выработку ориентации на профессии, существенным образом связанные в перспективе с математикой.

В последнее время наряду с увеличением в России количества классов с углубленным изучением математики и, как это ни парадоксально, заметным сокращением потребности в соответствующих специалистах, отсутствием достаточного количества хорошо подготовленных учительских кадров объективно стало наблюдаться снижение уровня математической подготовки выпускников данных классов. Об этом говорят итоги независимых экзаменов в ряде городов страны.

Принятая в соответствии с образовательной программой большинства школ (классов) данного профиля система обучения оправдывает себя в основном через решение систем задач. Однако, во-первых, времени для реализации такой системы должно быть достаточно, а во-вторых, при этом должна реализоваться методика обобщений. Однако личный опыт работы в университете, подкрепленный анализом современной педагогической и методической литературы, показывает, что многие студенты-первокурсники естественно-научных, и особенно математического, факультетов университета, в том числе и выпускники математических школ и классов, испытывают серьезные трудности, прежде всего на первых этапах обучения в высшей школе, при изучении математических теорий высокого уровня абстракции. Поскольку в классы с углубленным изучением математики поступают, как правило, тс дети, которые связывают свое будущее если не с математикой, то с естественно-научным циклом дисциплин, постольку еще в средней школе следует готовить их к преодолению упомянутых трудностей.

Таким образом, выявляются проблемы поиска альтернатив, учитывающих современную российскую реальность, вариантов обучения математике в школах (классах) с углубленным ее изучением и разработки содержания учебного материала.

Материал нашей статьи (см.: Чуча-ев И. И., Табачкова М. Ю. Симметрии графиков функций и уравнения // Математика в школе. 1997. № 6. С. 77 — 80), в которой уравнения решались приемами, использующими симметричность (инвариантность, неизменность) графика функции f(x) относительно некоторых преобразований области определения, может быть использован учителями математических школ и классов с углубленным изучением математики. Эти приемы могут быть перенесены и на системы уравнений специального вида.

Рассмотрим системы вида где f, g, h — функции одной переменной, а 1 — функция двух переменных.

Если р — инвариант функции f, то решения системы

Хб(х)) = h(y), 1(х, у) = О, содержащиеся в ОДЗ системы уравнений (1), являются решениями системы (1).

Заметим, что системы вида (1) стали появляться среди олимпиадных и конкурсных задач (см., например: Третья Со-ровская олимпиада школьников 1996 — 1997 гг. М., 1997; Горнштейн П. И. и др. Задачи с параметрами. М., Харьков, 1998).

Приведем примеры решения систем.

Пример 1. Решите систему уравнений х4 - 4х2 -т 2 | 2 - х2 | + 4 = 9у2 Т 6 | у | , х2 - бху = 0.

Решение. Система уравнений имеет вид (1), где

f(t) = I2 + 2 | 1 | g(x) = 2-х2, h(y) = Зу.

Функция f(l) четная и возрастающая при t > 0. Поэтому первое уравнение системы равносильно совокупности уравнений 2 - х2 = ±3у, а система равносильна совокупности систем уравнений

2 - х2 = Зу, 2 - х2 = -Зу, х - бху = 0, х — бху = 0.

Решая их, получаем следующие решения исходной системы:     (0;     ±2/3),

((-1±ТЛ)/4; (-1±733)/24), ((1±/33)/4; (-1 ±733")/24).

Пример 2. Решите систему уравнений

/4-х    _ Ту

< 10 - 2х + Т4 - х 2у - 2 + Ту -7 ’ ху + 2х = 1.

Решение. ОДЗ первого уравнения: х < 4, у > 2. Положим

f(t) = t/(2t2 + 1 + 2),_g(x) = ТТ-х h(y) = Ту -T

Тогда система записывается в виде (1). Так как при всех I ^ 0

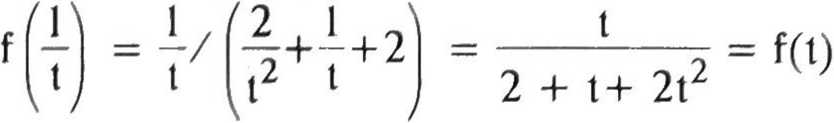
то функция >(1) = 1/1 — инвариант функции f(t). Поскольку каждое свое значение функция f(t) принимает не более двух раз, то первое уравнение системы равносильно совокупности уравнений

Т4 - х = Ту -"7, Т4 -х = 1 /Ту -2, а система равносильна совокупности систем уравнений

Т4 - х = Ту -7, ху + 2х = 1,

Т4 - х = 1 /Vy ху + 2х = 1.

Решая их, находим решения исходной системы: (4 ± VT5; 2 ± 715), (4/(9 ± /65); (1 ± Т55)/4).

Пример 3. Решите систему уравнений

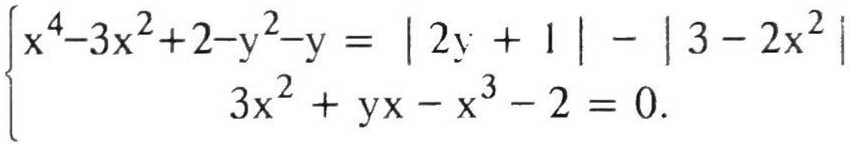
Решение. Перепишем первое уравнение в виде

(1 - х2)2 + 1 - х2 + I 2(1- х2) + 1 I = у2 + у + | 2у + I |

Тогда

f(t) = Г + t + I 21 + 1 I g(x) = 1 - х2, h(y) = у, и система примет вид (1). Графики фун-кций 1" + 1, | 21 + 1 | симметричны относительно прямой 1 = -1/2, поэтому pW =-l-t является инвариантом функции f(l). Функция f(t) возрастает при 1 > -1/2. Поэтому первое уравнение системы эквивалентно совокупности уравнений у = 1 - X2, -1 - у = 1 - X2, а исходная система равносильна совокуп-ности систем уравнений у = 1 - х2,

Зх2 + ху - 2 - X3 = О, -1 - у = 1 - X2.

|3х2 + ху - 2 - х3 = 0.

Решая их, находим решения исходной ^истомы: (1; 0), ((1 ± VT7)/4; (-1±Л7)/8), ((l±v7)/3: (-10±2v7)9).

Пример 4. Решите систему уравнений

Тогда первое уравнение системы примет

вид

Так как

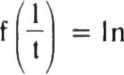
2t2 + 1 t2 + 2

= ПО.

. Гх + 21 .      . Гу+1"] ।

. I                I = |у- 1 -4         | у - 2у + 1 = 2х, где | х | — целая часть числа х.

Решение. Система уравнений

имеет

вид (1).

причем

f(t) = | t - 4

то функция ^(t) = 1/t — квазиинвариант f(t). Если х = 0, то система нс имеет решений. Поэтому далее будем считать, что х ^ 0. Тогда первое уравнение системы равносильно уравнению

f(h(y)) = f(l/g(x)).

Функция f(l) четная. Так как

g(x) = х, h(y) = у - 1.

Так как

f(t + 4) = | t + 4 - 4

t+2

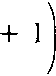
то функция f(t) периодическая,

= 40,

Т = 4.

Если

HI

< 2, то

t + 2

значит,

f(t) = | I | При этом f(2) = 2, f(-2) = 2. Отсюда следует, что функция f(t) четная и на |0; 2] строго возрастающая. Поэтому первое уравнение системы равносильно совокупности уравнений

_{гт =} 214+1 2t(2t² + 1) - 4t(t² + 2) _ ^U t² + 2        (2t²+l)²

-6t

(t2 + 2) (2t2 + 1) ’ то функция f(t) убывающая при t > 0. Отсюда следует, что первое уравнение системы равносильно совокупности уравнений у4-3 = ±1/х, а исходная система равносильна совокупности систем уравнений

х = у - 1 4- 4п, -х = у - 1 4- 4n, n Е Z,

у + 3 = 1/х, f у43 = -1/х, ух 4- у2 4- Зх = 5, ух 4- у2 4- Зх = 5.

Отсюда получаем решения системы: (1; 2), (1/5; 2к ((-3 ± VF)/3; ± VI).

а исходная система равносильна совокупности систем х = у - 1 4- 4п,    [-х = у - 1 4- 4п, у2 - 2у 4- 1 = 2х, у2 - 2у + 1 = 2х.

Решая их традиционным способом, получаем решения: (1 ± VI + 8п 4- 4п; 2±V1 +8п), где n>0, n Е Z и (l-V1^8n-4n; VI -IF), где п < 0, n Е Z.

Квазиинварианты функции f(t) могут быть использованы при решении систем, в которых первое уравнение имеет вид f(g(x)) 4- f(h(y)) = 0.        (3)

Рассмотрим примеры.

Пример 5. Решите систему уравнений

• , х² 4- 2     , у² 4- бу 4- 11      „

• In—~---4- In-²^-----------= 0,

• <   2х² 4-1      2у² + 12у 4- 19

ух 4- у2 4- Зх = 5.

Решение. Допустим

I2 4 2

f(t) = In—----» g(x) = х, h(y) = у 4- 3.

2г 4- 1

Пример 6. Решите систему уравнений х2+1    .   .

-^g Iх н

9у2-6у + 2 ' Зу - 1

1g | Зу - 1 | = 0,

х 4- ху - у2 = 0.

Решение. ОДЗ уравнения: х ^ 0, у ^ 1/3. Первое уравнение системы имеет вид (3). Положим

I2 4- 1

НО = —-— 1g | t | , g(x) = X, h(y) =3y-l.

Поскольку функция f(t) нечетная, то первое уравнение системы можно записать как f(-g(x)) = f(h(y)). Функция ^(t) = -1/t — инвариант f(t). Так как f'(t) = (I - l/t2)lgt + (1 + l/t2)lgc > 0

при t > 0, то функция f(t) является возрастающей при t > 0 и, следовательно, каждое свое значение может принимать нс более двух раз. Поэтому на ОДЗ пср- вое уравнение системы равносильно совокупности двух уравнений

-х = Зу - 1, 1 /х = Зу - 1, а исходная система равносильна совокупности систем уравнений

-х = Зу - 1, J 1/х = Зу - 1, [ х 4- ху - у2 = 0, х + ху - у2 = 0.

Решая их, получим, что исходная система имеет решения: ((7 ± 3 VT)/4; (-1 + 75)/4), (1/2; 1).

О МЕТОДИКЕ ИЗУЧЕНИЯ ЯЗЫКА ПРОГРАММИРОВАНИЯ TURBO PASCAL НА ФАКУЛЬТАТИВНЫХ ЗАНЯТИЯХ ПО ИНФОРМАТИКЕ

Основным понятием информатики является понятие информации. Почти полвека тому назад американский ученый, отец кибернетики Норберт Винер дал такое определение информации: „Информация есть информация, не материя и не энергия" Но несмотря на свою нематериальную сущность, информация служит определяющим фактором развития экономической, технической, научной и других сфер человеческой деятельности. Информация обладает замечательным свойством: если се аккумулировать и обрабатывать, то она даст новые сведения и приводит к новым знаниям. Она также позволяет человеку ориентироваться в окружающем мире, обеспечивает его жизнедеятельность.

Последняя четверть нашего столетия отличается мощным информационным взрывом. Ежегодно в мире публикуется около 100 тыс. журналов на 60 языках, выходит более 5 млн научных ста тей, книг, брошюр, защищается более 250 тыс. диссертаций. Ежеминутно в мире публикуется около 2 тыс. печатных страниц научных текстов: каждые 1,5 — 2 мин предлагается новое техническое решение; каждый час регистрируется 15 — 20 научных изобретений и открытии. Невозможность своевременно аналитически охватить все научные достижения может привести к частичному дублированию исследований, увеличению сроков разработок, отставанию в системе образования и т. д. Материалы американской статистики свидетельствуют о том, что каждая десятая исследовательская работа является излишней, так как была проделана ранее и результаты се где-то были опубликованы. И это в одной из самых компьютеризованных стран ми-ра! *х

По данным ЮНЕСКО, каждый ученый, разработчик или исследователь половину своего времени расходует на по-