Использование системы компьютерной алгебры Maple на занятиях по дифференциальной геометрии

Дифференциальная геометрия - один из разделов геометрии, изучаемый в процессе подготовки учителей в педагогических вузах. В дифференциальной геометрии изучаются геометрические образы (свойства кривых и поверхностей в малом, семейств линий и поверхностей) методами математического анализа. Для эффективного освоения курса дифференциальной геометрии студенты должны обладать достаточно высоким уровнем развития пространственного воображения и пространственного мышления. Без этого невозможно интерпретировать аналитически полученные результаты применительно к конкретному геометрическому объекту, поэтому при исследовании свойств кривых и поверхностей в пространстве важно опираться на принцип наглядности в обучении.

Для представления в наглядной форме трехмерных геометрических объектов можно создавать предметные модели. Наглядные материальные модели часто используют в процессе обучения, но их создание отнимает много времени и средств, причем зачастую материальные модели статичны и не предусматривают интерактивности при изучении свойств моделируемого объекта. Этих недостатков лишены модели, созданные на основе информационных технологий. Такие модели, демонстрирующие свойства геометрических объектов, могут быть открыты для модификации, изменения параметров, задающих поверхности и кривые, изучающими их студентами. Программное обеспечение и информационные ресурсы, которые могут оказаться полезными при обучении студентов дифференциальной геометрии, довольно разнообразны:

• -    специализированные пакеты для геометрических построений (GeoGebra, Cabri 3D, GeomSpace, Geometer’s SketchPad и др.);

• -    универсальные математические пакеты Maple, Mathematica, Matlab, Axiom, Maxima и др.;

• -    системы автоматизированного проектирования и инженерной графики;

• -    графические редакторы с развитыми геометрическими возможностями;

• -    готовые рисунки, чертежи и анимации, доступные в сети Интернет (особенно много подходящих рисунков имеется в математической онлайн-энциклопедии MathWorld.Wolfram и в англоязычной Википедии).

Наконец, требуемые рисунки и анимации могут быть результатом работы программы, созданной в какой-то универсальной среде программирования, например Delphi. Однако этот путь, с учетом перечисленных выше требований, конечно, очень затратен и не слишком рационален.

Системы автоматизированного проектирования и инженерной графики, как правило, дороги и не просты в освоении. Использование готовых рисунков и чертежей, созданных в графических редакторах, не позволяет преподавателю или самим студентам изменять параметры, задающие те или иные геометрические объекты, чтобы отслеживать и анализировать геометрическую сущность этих параметров. В связи с этим естественно остановиться на одном из специализированных геометрических или универсальных математических пакетов. Возможна, конечно, и комбинация различных пакетов. Например, В. Глизбург, являющаяся одним из ведущих специалистов в интересующей нас области, рекомендует комбинацию Maple + Cabri [1]. Однако при том количестве часов, которое отводится учебными планами на изучение дифференциальной геометрии, тратить время на освоение сразу двух математических пакетов – непозволительная роскошь.

Мы остановили свой выбор на системе компьютерной алгебры Maple. В пользу такого решения говорят следующие факты.

• 1.    Богатые возможности трехмерной графики системы Maple: возможность совмещения геометрических объектов различной природы на одном чертеже; возможность вращения и модификации готовых графических объектов; простота создания анимаций и др.

• 2.    Мощная система символьных вычислений. Это позволяет использовать Maple не только для обеспечения наглядности, но и для выполнения достаточно громоздких преобразований математических формул и выражений, с которыми приходится иметь дело при изучении дифференциальной геометрии.

• 3.    В Maple имеется подгружаемый пакет DifferentialGeometry. Сосредоточенные там команды и функции ориентированы на внутреннюю геометрию поверхности, тензорное исчисление, алгебры Ли. В базовом курсе дифференциальной геометрии изучение этих тем не предусмотрено. Однако тем студентам, тематика выпускных квалификационных работ которых будет связана с дифференциальной геометрией, не придется переучиваться.

• 4.    Знакомство с Maple будет востребовано в дальнейшем: при изучении компьютерной алгебры, информационных технологий в математике, а также, возможно, ряда спецкурсов и некоторых дисциплин, изучаемых в магистратуре.

В пользу Maple говорит и наличие в Волгоградском государственном социально-педагогическом университете электронного учебника, с помощью которого студенты могут быстро и эффективно получить навыки первоначальной работы c данным математическим пакетом [4].

Безусловно, немалую роль в выборе математического пакета для поддержки курса дифференциальной геометрии сыграли и личные предпочтения авторов. Система компьютерной алгебры Maple – один из лидеров среди систем символьной математики. Для многих математических задач, решаемых по определенному алгоритму, в Maple имеются соответствующие команды. Maple обладает мощными средствами визуализации вычислений и математических понятий, обеспечивает управляемые пользователем возможности отображения информации на экране, позволяет минимальными средствами создавать свои эффективные программы [3].

Учебным планом изучения дифференциальной геометрии предусмотрены как лекции, так и практические занятия (семинары). Нам представляется уместным использование Maple и при изложении теоретического материала, и при его закреплении на практике.

При изучении теории использование созданных в Maple чертежей и анимаций позволяет визуализировать дифференциально-геометрические понятия. Важным является то, что даже статические 3D-объекты можно вращать и рассматривать с разных сторон. Например, при изучении темы «Сопровождающий трехгранник» студентам можно предъявить чертеж, на котором представлены участок кривой, а также касательная, главная нормаль и бинормаль в одной из точек, принадлежащих кривой. Рассмотрения рисунка с одного, даже самого удобного, ракурса может оказаться недостаточно для выявления поведения кривой в окрестности данной точки, поэтому уместно рассмотреть чертеж с разных ракурсов. Так, выбирая направление проектирования близким к направлению бинормали, можно увидеть «плоский портрет» нашей кривой, наиболее близкий к оригиналу, а проектируя в направлении, близком к направлению главной нормали, мы увидим картину, объясняющую происхождение термина спрямляющая плоскость .

Используя возможности трехмерной графики системы Maple, можно показать не только касательную бинормаль и главную нормаль, но и особенности расположения относительно кривой взаимно перпендикулярных граней ее сопровождающего трехгранника. На рисунках 1а – 1в, наряду с касательной (зеленая линия), бинормалью (красная линия), и главной нормалью (синяя линия), поочередно представлены соприкасающаяся, нормальная и спрямляющая плоскости в неособой точке кривой.

Как показывает опыт, большинство студентов плохо понимают, что представляет собой соприкасающаяся плоскость (предельное положение плоскости, проходящей через три неограниченно сближающиеся точки кривой) и чем она отличается от остальных касательных плоскостей к кривой в данной точке. Графиче-

ские возможности Maple позволяют показать (рис. 1а), что вблизи точки прикосновения кривая расположена по разные стороны от соприкасающейся плоскости.

Полезно обратить внимание студентов на бесконечность множества нормалей к кривой в каждой ее точке. Все они расположены в нормальной плоскости, определяемой главной нормалью и бинормалью к кривой (рис. 1б). В рассматриваемой точке кривая «протыкает» нормальную плоскость

На рисунке 1в наглядно видно, что, в отличие от соприкасающейся и нормальной плоскостей, в окрестности рассматриваемой точки кривая расположена по одну сторону от спрямляющей плоскости. При этом из всех касательных плоскостей кривая максимально быстро удаляется именно от спрямляющей плоскости. Заметим, что при демонстрации можно менять кривую, выбирать разные точки кривой, для которых рассматриваются сопровождающие трехгранники, менять параметры просмотра.

Еще более наглядным понятие «сопровождающий трехгранник» станет, если рассмотреть его в динамике, когда точка, в которой строится сопровождающий трехгранник, движется вдоль кривой. На рис. 2 представлены три стоп-кадра соответствующей анимации.

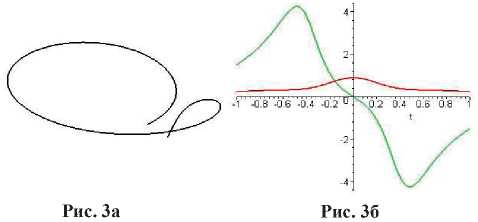
Использование Maple при обучении дифференциальной геометрии не сводится исключительно к созданию иллюстраций и анимаций. При нахождении единичных векторов сопровождающего трехгранника, коэффициентов в формулах Френе-Серре, кривизны и кручения кривой, заданной в обычной и естественной параметризациях, можно использовать возможности символьных вычислений Maple. Следует обратить внимание студентов на то, что кривизна показывает, насколько отклоняется кривая по своей форме от формы прямой (чем больше кривизна, тем больше это отклонение), а кручение показывает, насколько отклоняется пространственная кривая по своей форме от формы плоской кривой (чем больше кручение, тем больше это отклонение). Можно не только находить кривизну и кручение кривой в конкретной ее точке, но и представлять их как функции от параметра. Построив графики изменения функций кривизны и кручения кривой в зависимости от изменения параметра в одной системе координат (рис. 3б) и вращая построенную в Maple кривую (рис 3а), можно показать взаимосвязь кривизны и кручения с поведением кривой.

Следующий пример еще более выпукло иллюстрирует мощь вычислительных возможностей Maple. На практическом занятии, посвященном изучению пространственных кривых, можно решить такую задачу: «намотать» кривую на стержень, закрученный в форме винтовой линии. Параметрическое уравнение требуемой кривой легко получить, используя несколько прозрачных команд Maple.

> with(plots):

> x:=cos(t);x1:=diff(x,t);x2:=diff(x1,t):

> y:=sin(t);y1:=diff(y,t);y2:=diff(y1,t):

> z:=t/2;z1:=diff(z,t);z2:=diff(z1,t):

> c:=1/4:b:=1/18:

> X:=x+b*x1+c*(x2*sin(t/b)+(y1*z2-z1*y2)*cos(t/b)):

> Y:=y+b*y1+c*(y2*sin(t/b)+(z1*x2-x1*z2)*cos(t/b)):

> Z:=z+b*z1+c*(z2*sin(t/b)+(x1*y2-y1*x2)*cos(t/b)):

>spacecurve([X,Y,Z,numpoints=700],t=-1..4*Pi, thickness=3):

Чтобы убедиться, что без использования математического пакета решить задачу было, мягко го- воря, затруднительно, достаточно распечатать заданные ранее уравнения:

Y = sin(t)+16384 cos(t)¹⁹ - 90112 cos(t)¹⁷ + 207872 cos(t)¹⁵ - 261632 cos(t)¹³ + 195520 cos(t)¹¹ –

– 88352 cos(t)⁹ + 23496 cos(t)⁷ – 3396 cos(t)⁵ + ⁸⁹ ₄ ⁷ cos(t)³ – ³ ₇ ¹ ₂ ¹ cos(t)

Построив изображение кривой, задаваемой полученным уравнением, убедимся, что задача решена верно (рис. 4).

До сих пор мы рассматривали примеры использования Maple при изучении пространственных кривых. Разумеется, вычислительные и графические возможности системы компьютерной алгебры Maple при-

X = 1732 13 sin(t) – 16384 sin(t)cos(t)18 + 57344 sin(t)cos(t)16– 76800 sin(t)cos(t)14 + + 46592 sin(t)cos(t)6 – 300 sin63cos(t)4 + 63 sin (t) cos(t)2 + cos(t)

годятся и при изучении поверхностей. Касательная плоскость, нормальные сечения, координатные линии на поверхности, геодезические, главные кривизны, индикатриса Дюпена, типы точек на поверхности, гауссова кривизна, внутренняя геометрия поверхности, минимальные и линейчатые поверхности, квадратичные формы поверхности - при освоении студентами всех этих понятий помощь Maple может существенно сократить время расчетов и повысить наглядность воспри-           ^ис.

ятия [2]. Остановимся только на одном примере: развертывание цилиндра на плоскость (рис. 5). Этот пример будет полезен и при изучении темы «Развертывающиеся поверхности» и при рассмотрении более общего вопроса об изгибании поверхностей.

Отметим, что наиболее целесообразно не предъявить студентам готовую анимацию, а разработать ее вместе с ними. Для этого помогут такие вопросы, адресованные студентам:

• -    какова траектория каждой точки при развертывании цилиндра на плоскость?

• -    как выглядит параметрическое уравнение циклоиды?

• -    чем отличаются циклоиды, описываемые разными точками цилиндра?

• -    как «заставить» разные точки цилиндра закончить движение в разные моменты времени?

Найдя ответы на эти вопросы, студенты под руководством преподавателя разработают компактную с точки зрения размеров кода, но не простую в реализации анимацию.

>animate(plot3d,[[2*Pi*('if'(t+u<1,t+u,1)-u)- sin(2*Pi*'if'(t+u<1,t+u,1)),v,

1-cos(2*Pi*'if'(t+u<1,t+u,1))],u=0..1,v=0..4], t=0..1,scaling=constrained,orientation=[-70,70]);

После того как студенты получат первоначальные навыки работы с Maple, уместно приобщать их к самостоятельному созданию графических образов и анимаций по изучаемой тематике. Польза от такого рода деятельности будет двойной: более глубокое освоение материала дифференциальной геометрии, освоение СКА Maple. Последнее будет полезным не только в качестве пропедевтики дисциплины «Информационные технологии в математике», но и в дальнейшей профессиональной деятельности.

Применение математических пакетов, в частности системы компьютерной алгебры Maple, в процессе обучения дифференциальной геометрии способствует лучшему пониманию студентами теоретического материала и осознанному применению его на практике. Возможность интерактивного изменения параметров при вычислениях и демонстрации объектов повышает самостоятельность и развивает познавательные способности студентов.