Использование сложных гармонических сигналов в задачах акустической спектрометрии эластомеров

Термомеханические методы исследования свойств эластомеров находят широкое применение в практике лабораторного и промышленного контроля качества. Термомеханические методы обладают простотой реализации и высокой информативностью, а также позволяют определить большое количество свойств эластомеров и их композитов (аморфность или кристалличность, влияние пластификаторов и наполнителей, температуры размягчения, стеклования, плавления, кристаллизации и т.д.). Широкая сфера применения термомеханического метода привела к созданию разнообразных приборов и методов контроля, предназначенных для определения конкретных показателей качества, использующихся в той или иной отрасли промышленности. Каждый из методов контроля характеризуется своим частотным диапазоном деформации испытуемого образца, температурным диапазоном и соответствующей методике единицей измерения (единицы вязкости по Муни, пластичности по Карреру и т.д.). Современные методы формирования и регистрации механических деформаций, которым подвергается эластомер, позволяют моделировать температурночастотные условия разных методов контроля в рамках одного прибора, что открывает широкие возможности для создания универсальных, компактных и недорогих систем контроля спектра показателей качества эластомеров.

Разрабатываемая система контроля должна обеспечивать нанесение возмущающего сигнала на испытываемый образец, регистрацию прошедшего через образец сигнала и его обработку с целью соотнесения шкалы измерения регистратора и единицы измерения показателя качества эластомера.

Оценка показателей качества осуществляется по измеряемым акустическим свойствам образца [1]. По измеренным параметрам колебательных процессов, возбуждаемых в образце ультразвуковым преобразователем (амплитуд излученного и принятого сигналов Аизл, Апр), регистрируемых приемником и ос циллографом для передачи на ЭВМ, а также условий проведения измерений (частоты о, Гц и температуры T, К) и толщины образца (h, м) определяются акустические свойства полимера (а - коэффициент затухания, м-1; c - скорость звука, м/с;) при заданных о и T :

c = —, а = — • ln A"' , A а      2 h   А пр

где Ata - время прохождения сигнала от излу чателя до приемника.

Анализ проводится как при фиксированных температурах и частотах воздействия, так и на основе акустической спектрометрии (сканировании в частотном или температурном диапазоне с определенным шагом). В результате сканирования формируется множество значений, отражающих распределение акустических свойств полимера по температуре и частоте Sak = (a , ,c ,,о,, Ao,T , A T ), i = 1,N . По этим значениям осуществляется расчет распределений компонентов комплексного модуля упругости E или тангенса угла механических потерь tg5 Svp = (Е,,n , ,tg5 , ,о , , A o , T , A T }, , = 1,N .

E ( о ) = E ' + ion = pc ²

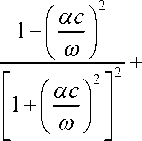
ac

E

+ i • 2 pc ² • ------------ -y, tg5 -

^{2 2} E

Показатели качества, как правило, увязывают с параметрами кривой, полученной по данным акустической спектрометрии [2]. Например, температура релаксационного или фазового перехода Tп в диапазоне T е[ Tn min, Tn max ] при частоте измерения оо определяется как:

T n = ^ma^x ( ^tg ⁵ ( ^o o^, T ) ) , ⁽³⁾ время релаксации т_Р при температуре T ₀ определяется по частотной характеристике тангенса угла механических потерь:

^{Т р =} { m | x [ tg ⁵ ( о, T o ) ] } . (⁴)

По данным акустической спектрометрии можно оценить спектр времен релаксации полимера [3] и даже функцию молекулярномассового распределения его раствора [4].

Необходимость оперативности контроля показателей качества требует максимального сокращения суммарного времени цикла анализа, включающего нанесение, регистрацию и обработку результатов воздействия при каждом шаге воздействия в процессе сканирования. Сокращение времени измерения возможно сужением диапазона сканирования или увеличением шага Ao, AT . В первом случае потеря полезной информации возможна в результате выхода за пределы частотного или температурного диапазона измерения, а во втором - за счет снижения частоты дискретизации.

Выходом из данной ситуации служит использование в качестве возмущающего сигнала не гармонического сигнала одной частоты го, а сложного гармонического сигнала, являющегося суперпозицией нескольких гармонических сигналов с информативными для конкретной задачи частотами го gQ , например Q = { 1,3,5,10 } . Такой подход используется при исследовании динамических систем, таких как радиотехнические цепи [5].

В таком случае для селективности анализа излучаемых и принимаемых после прохождения через образец сигналов необходим способ независимого оценивания потерь для каждой из гармоник. Такие возможности представляет аппарат спектрального анализа [6]. Одним из эффективных способов является разложение исходного сигнала S ( t ) в диапазоне t g [ t 1 , t ₂ ] , для которого выполняется условие:

t 2

j[S (t)] dt <«           (5)

t 1

в систему ортогональных функций { ф _п ( t ) } :

«

Система представляет собой обобщенный ряд Фурье (6), причем каждый член ряда

C_nФ_n ( t ) является спектральной составляющей, а совокупность коэффициентов { C ₀,..., C_n ,... } -спектр сигнала S ( t ) . Суть спектрального анализа заключается в определении коэффициентов ряда (6). Кроме того, возможна как аппроксимация, так и разложение S ( t ) с последующим анализом спектральных составляющих. Таким образом, эффективным средством исследования свойств эластомеров является использование сложных излучаемых акустических сигналов, состоящих из некоторого множества спектральных составляющих { C ₀,..., C_n ,... } . В реальном исследовании предполагается конечное число спектральных составляющих N g [ n 1 , n ₂ ] , обеспечивающих решение частной исследовательской задачи.

n 2

S ( t ) « Z C n Ф n ( t ) (7) n = n

Например, метрологические характеристики (чувствительность как отношение изменения измеряемого косвенного параметра к изменению показателя качества и погрешность оценок показателей качества) при измерении предельной прочности при разрыве c P и вязкости по Муни Mh по данным экспериментальных исследований [2] существенно зависят от частоты и температуры. В таблицах 1, 2 представлены результаты оценки погрешностей.

Таблица 1

Относительные погрешность и чувствительность оценки c P для каучука СКС-30

Частота измерения, МГц	0,6	0,6	1,25	2,5
Температура измерения, K	373	293	293	293
Максимальная относительная погрешность, %	28,422	31,796	21,28	7,216
Средняя относительная погрешность, %	14,039	13,992	8,653	4,283
Относительная чувствительность	0,037	0,017	0,287	0,816
Критерий Фишера (расчетный)	0,197	0,352	2,55	3,229

Таблица 2

Относительная погрешность и чувствительность оценки Mh для каучука СКС-30

Частота измерения, МГц	0,6	0,6	1,25	2,5
Температура измерения, K	373	293	293	293
Максимальная ошибка, %	1,933	2,465	9,356	9,318
Средняя ошибка, %	0,952	1,438	4,373	3,518
Относительная чувствительность	0,159	0,192	0,033	0,017
Критерий Фишера (расчетный)	4,49	4,6	0,383	0,48

Видно, что наилучшие характеристики по каждому показателю достигаются при определенных частотах ro M _h и го *

Таким образом, целесообразно вести измерения с использованием сложных гармонических сигналов, представляющих суперпозицию нескольких гармонических сигналов с частотами, соотвествующими максимумам чувствительности и минимуму погрешности измерения для каждого показателя качества в общем случае:

N

^S l ( t ) = i A n sin ( ® n t + Ф п ) ,      ⁽⁸⁾

n = 1

и для случая анализа предельной прочности при разрыве и вязкости по Муни:

S z ( t ) = A Mh sin ( ® Mh t + Ф мh ) + + A _cp sin ( ® * P t + Ф _{с р} )

где S _z ( t ) - сложный гармонический сигнал,

An, AMh , Aap , Фп, Фмн, фар - амплитуды и фазы соответствующих составляющих гармоник сложного сигнала.

Далее, используя преобразование Фурье прошедшего через образец и принятого сигнала, определяются зоны частотных диапазонов, соответствующих максимумам в спектре при -нятого сигнала. Значения функции спектра характеризуют амплитуды соответствующих частот и, следовательно, отражают изменение этих амплитуд с изменением свойств материала в заданном частотном диапазоне (рисунок 1).

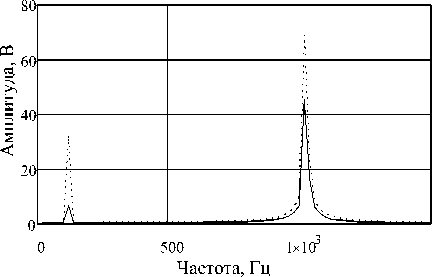
Рисунок 1. Пример амплитуд сигнала для определения двух показателей качества

Однако на первом этапе исследований заранее не известен набор необходимых для исследования частот или хотя бы их диапазон. В таком случае для исследований и выявления необходимых частотных диапазонов можно использовать сигнал типа белый шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот.

S ( го ) ^ const , VroG ( —»; +да ) (10)

Одним из эффективных способов его использования является определение частотных характеристик динамических систем, т.к. амплитудно-фазовая частотная характеристика линейной системы есть отношение преобразования Фурье выходного сигнала к преобразова- нию Фурье входного сигнала [5]. Также воздействие сигнала белый шум на вход системы используется в задачах идентификации динамических систем [5].

В генераторах есть возможность синтеза сигналов, моделирующих белый шум. Однако при осуществлении исследований у такого подхода возникает ряд трудностей – вероятность искажений из-за ограничений на время регистрации сигнала белого шума при фиксированном количестве точек сигнала, в связи с ограничением памяти регистратора осциллографа. При малых интервалах времени возникают искажения в низкочастотной области спектра, а при больших сигнал искажается в высокочастной области ввиду снижения частоты дискретизации и, соответственно, потери информации. На рисунках 2, 3 представлены спектры сигнала белый шум, регистрация велась с помощью цифрового осциллографа RIGOL DS-1102.

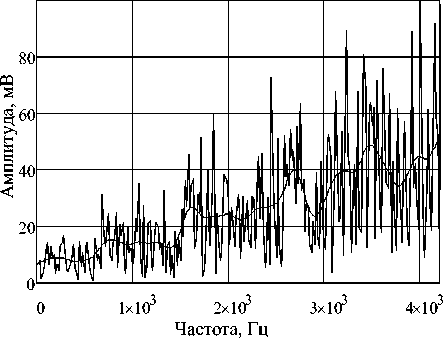
Рисунок 2. Спектр сигнала белый шум, записанный с помощью осциллографа RIGOL DS-1102

Представленные спектры получены для интервалов сигнала белый шум 4 - 10 — 6 , 4 - 10 — 2 и 1 секунда, для визуализации результатов дополнительно использовалась фильтрация по алгоритму на основе ядра функции Гаусса (рисунок 2). Из представленных на риунке 3 спектров видно, что с изменением интервала времени, при котором регистрируется спектр, довольно существенно проявляется отклонение от равномерного распределения спектральных составляющих по частотам.

В этой ситуации для синтеза автоматизированных информационно-измерительных систем необходимо разработать методику выбора интервала времени подачи сигнала типа белый шум, который обеспечивал бы приемлемое качество фиксируемого сигнала в смысле равномерности распределения спектральных составляющих в наблюдаемом частотном диапазоне.

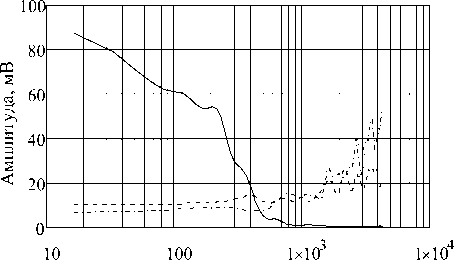
Частота, Гц

― 4*10-6 сек; - - - 0,04 сек; - · - 1 сек.

Рисунок 3. Спектры сигналов «белый шум» с различным временем регистрации

Таким образом, в системах акустической спектрометрии свойств эластомеров, возможна оценка нескольких показателей качества с использованием сложных гармонических сигналов, что позволит повысить оперативность измерений в частотном диапазоне, обеспечивающем приемлемые метрологические характеристики измерений. Для использования на начальном этапе исследований сигналов в виде стационарного белого шума необходимо разработать процедуру подбора временного окна, при котором обеспечивается равномерность спектральных составляющих излучаемого генератором сигнала.