Использование средств информационных технологий для изучения моделей нелинейной динамики

Потребность общества в высококвалифицированных специалистах, способных решать задачи различной сложности, адаптироваться к изменяющимся условиям, готовых к саморазвитию и самообучению, повлекла за собой изменения в образовательной системе. Требования, предъявляемые к выпускникам вузов, изложены в Федеральном государственном образовательном стандарте (ФГОС), построенном на компетентностном подходе [1,2]. Среди требований следует выделить способность приобретать новые научные и профессиональные знания с использованием современных образовательных и информационных технологий (ИТ) [3-8], способность собирать, обрабатывать и интерпретировать данные современных научных исследований, необходимые для формирования выводов по соответствующим научным исследованиям. Таким образом, для достижения поставленных обществом и государством целей обучения, выражающихся в формировании необходимых компетенций, перечисленных выше, нужно организовать учебный процесс на основе адекватного целям содержания образования, широкого использования средств ИТ, реализации межпредметных связей учебных дисциплин [9]. Инструментом интеграции в процессе обучения математическим дисциплинам студентов, обучающихся по направлению подготовки «Прикладная математика и информатика», может служить математическое и компьютерное моделирование [1013]. Средства ИТ позволяют преобразовать математическую модель в компьютерную при наличии формального описания первой. ИТ представляют широкие возможности визуализации результатов моделирования, такие как построение графиков, диаграмм и т.п. Вопросу использования средств ИТ в образовательном процессе и научноисследовательской работе посвящено много работ [5-8].

Читаемая студентам бакалавриата, обучающимся по направлению подготовки «Прикладная математика и информатика», дисциплина «Качественные методы нелинейной динамики» как раз решает задачи формирования компетенций, связанных с выполнением фундаментальных и прикладных работ поискового, теоретического и экспериментального характера

В качестве примера использования ИТ в исследовательской работе приводится математическая модель виброударного механизма с кривошипношатунным возбудителем колебаний (КШВК), численное исследование которого проведено с помощью программного комплекса, разработанного в среде Borland C++ Builder 6.

Описание курса «Качественные методы нелинейной динамики»

Дисциплина «Качественные методы нелинейной динамики» относится к дисциплинам специализации, лекционным курсам по выбору студентов, специализирующихся в области прикладной математики, нелинейной динамики, математического моделирования.

Цели и задачи дисциплины «Качественные методы нелинейной динамики» состоят в том, чтобы

• -    ознакомить студентов с основными понятиями и современными методами нелинейной динамики и приемами исследования нелинейных динамических систем;

• -    привить студентам практические навыки математического моделирования процессов нелинейной динамики на основе качественно-численных методов исследования с применением компьютера, необходимые для решения конкретных прикладных задач нелинейной динамики.

Дисциплина «Качественные методы нелинейной динамики» изучается в 5 семестре. Изучаемый в рамках дисциплины теоретический и практический материал опирается на базовые знания, полученные обучающимися в результате освоения таких дисциплин как «Математический анализ», «Дифференциальные уравнения», «Численные методы».

Полученные в результате освоения данной дисциплины знания и навыки могут быть непосредственно применены обучающимися в их будущей профессиональной деятельности, а при продолжении ими обучения в магистратуре являются частью базовых знаний по дисциплинам, связанным с применением математических методов и компьютерного моделирования, при решении задач математического прогнозирования, системного анализа и оптимизации.

Анализ различных   источников,   посвященных   компьютерному моделированию, позволяет выделить несколько классов средств компьютерного моделирования для исследования математических моделей в зависимости от их функционала [9]

• -    языки и системы программирования (C++, Object Pascal и т.д.);

• -    математические пакеты аналитических и символьных преобразований (MathLab, Maple и т.д.);

• -    специализированные программы для исследования моделей (Ansys, AutoCad и т.д.).

Для исследования задач нелинейной динамики студентам предлагается в качестве средств ИТ написать собственную программу на языке программирования или воспользоваться одним из математических пакетов. Специализированные программы исследования моделей в данном случае не подходят, поскольку ориентированы на выполнение расчетов для других классов задач.

В качестве примера в работе приводится математического и компьютерного моделирование динамики виброударного механизма с КШВК [14,15].

Пример использования средств ИТ

Работу рассматриваемых вибрационных механизмов можно описать следующим образом (рис.1): вращательное движение с постоянной частотой ® вала основной массы механизма с помощью кривошипно-шатунного устройства преобразуется в возвратно-поступательное движение основной массы М относительно шабота. При этом ползуны-ударники попеременно наносят удары по h соответствующим наковальням высоты i и, создаваемое таким образом ударновибрационное воздействие передается непосредственно через шабот обрабатываемой среде. Благодаря выбору величин сдвига по фазе ^i между кривошипами, эксцентриситетов ri , высот наковален может быть обеспечено требуемое (может быть оптимальное в некотором смысле) ударное взаимодействие ползунов-ударников о шабот, при котором ползуны-ударники (ПУ) имеют максимальную скорость, обеспечивая устойчивость периодического режима работы. Следует отметить, что наличие в рассматриваемых механизмах нескольких ПУ создает условия к возникновению в простейших режимах движения в одном его цикле N ударов ПУ об обрабатываемую среду, что с одной стороны, как известно, должно способствовать более эффективному процессу пластического деформирования обрабатываемой среде, а с другой – несколько затрудняет процесс настройки механизма на этот эффективный режим движения и поэтому требует детальное предварительное математическое изучении его нелинейной динамики. Уравнения движения механизмов при ряде ограничений могут быть записаны в виде

X = - p , x >  f ( т ),

5c ⁺ =- RX ^- + (1 + R ) df ^ )-, x = f ( т ). d T

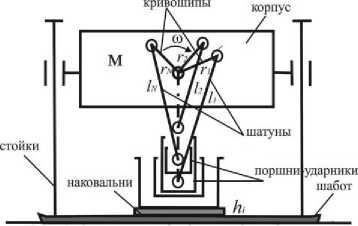
Рис. 1. Схема виброударного механизма с КШВК с произвольным числом поршней-ударников с неподвижным ограничителем где x, т - безразмерные координата центра масс и время соответственно, 0 < R < 1 -коэффициент восстановления скорости при ударе поршня о неподвижный ограничитель, моделирующий среду,    f (т ) = max{f(т), f2(т ),...,fN (т)}    - т цилиндрическая поверхность, ограничивающая движение фазовой точки в трехмерном фазовом пространстве. Фазовое пространство системы (1) в координатах x, x, т усечено по x , причем x > f(т), x < +«.Все фазовые траектории располагаются либо на поверхности S(x = f (т)), либо выше ее, представляющую собой как N пересекающихся поверхностей x = f(т) (i=1,2,...,N). Случай x. > f (т) соответствует свободному движению механизма, а x = f (т) - ударному взаимодействию одного из ПУ с ограничителем.

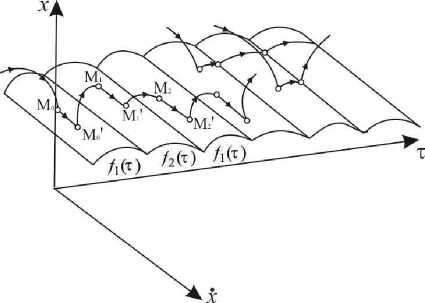
Рис.2. Качественный вид фазового пространства для двухпоршневого виброударного механизма с кривошипно-шатунным возбудителем колебаний

Исследование динамики механизма, описываемого дифференциальными уравнениями (1), (2), проведено, как и в [14], с помощью метода точечного преобразования [16]. За секущую поверхность выберем поверхность S.

Пусть

M о^{( т} = ^т о , х = ^f 1^{( т} о ), x = x о ) е S i⁽ х = ^f 1^{( т} )),

M 1 ( т = т 1 , x = f 2 ( т 1 ), x = ;c i ) е S ₂( x = f ₂ ( т )),

M2 (т = т2, x = f (т ),-x = ^x2 ) е S],   - три последовательные      точки, принадлежащие поверхности x = f (т) , тогда преобразование T = T^T точек TT

М_о-- ¹—> M]-- ²—> M₂ можно записать в виде

- цу cos(r 1 - ф") = - цХ ₁(cos т ₁ - cos t 0 ) - ( т 1 - т ₀)( цХ 1 sin т 0 + цуХ ₂ sin( T 0 - фУ) - (3)

T 1 1

- цуХ ₂ (cos( t - ф ) - cos( t 0

^- Ф» ^- Р ( ^Т 1 Т 0 )  ^{+ 51} о ^{( т} 1

- т 0 ) + £ - ц cos t 0 ;

x 1 = - R ( цХ ₁(sin т 1 - sin т 0 ) + цyХ ₂(sin( т ₁ - ф ) - sin( T 0 - ф )) - p ( т 1 - т 0 ) + x ₀) +

+ (1 + R ) цу sin( T 1 - ф );

£ - ц cos t 2 =- цХ ₁(cos т 2 - cos T 1 ) - ( т 2 - т 1 )( цХ 1 sin т 1 + цуХ ₂ sin( T 1 - ф )) -

T 2 1

- цуХ ₂ (cos( t ₂

- ф ) - cos( t - ф )) - Р

( т 2 - Т 1 ) 2 2

^{+ x} 1 ( ^T 2

- Т 1 ) - цу cos( T 1 - ф );

x ₂ = - R ( цХ 1 (sin т ₂ - sin т 1 ) + цуХ ₂ (sin( T ₂ - ф ) - sin( T 1 - ф )) - p ( т ₂ - т 1 ) + x 1 ) +

+ (1 + R ) ц sin т ₂.

В связи с усеченностью фазового пространства по фазовой координате, точечное преобразование T будет определено, если выполнены следующие неравенства

£ - ц cost 0 > - цу cos(t 0 - ф)

- цу cos(T1 - ф) > £ - цcosT1

£ - цcost2 >-цу cos(t2 - ф)

x(т) > f (т) для Т0 < Т < Т1, Т1 < т < т2,

Первое неравенство системы (7) означает, что в начальный момент времени т = т0 изображающая точка принадлежит поверхности S( x = f (т) ) (это условие соответствует ударному взаимодействию первого поршня о шабот), второе неравенство означает, что в момент времени т = т изображающая точка принадлежит поверхности S( x = f2 (т)) (это условие соответствует ударному взаимодействию второго поршня о шабот), третье неравенство означает, что в момент т = т2 изображающая точка вновь попадает на поверхность x = f (т) (вновь происходит ударное взаимодействию первого поршня о шабот). Четвертое неравенство отражает очевидный факт принадлежности изображающей точки подпространству x > f (т) .

Уравнения для нахождения неподвижных точек преобразования Т , соответствующих двухударным (с поочередными ударами каждым поршнем-ударником) периодическим движениям (основной режим) получаются путем добавления к (3) - (6) условий периодичности [17]

^x2 = x0 = x, т2 = т0 + 2.nn (8) Вводя в рассмотрение параметр ^ = Т1 - Т 0, характеризующий время движения изображающей точки между двумя последующими ударами поршней-ударников, получим уравнения для определения координат неподвижной точки в виде x = R(p(2nn - ^) - ;x1) + (1 + R)ц sin т0, p2

£ - цcost0 =- — (2nn - ^) + (2nn - ^)x:1 -

• -    цу cos(t0 + а).

;v1 = R ( p ^ - ;: ) + (1 + R ) цу sin( T 0 + а ),

• -    цу cos(r 0 + а) = - -p ^2 + ^x + £ -А к - ц cost 0,

(a = f - ф, f = Т1 - То )

Из первого и третьего уравнений (11) получим

■ х0 =

Rp(2 п п - f (1 + R )) + (1 + R ) p (sin т₀ - R y sin( T ₀ + а )) 1 - R ²

■

^Х 1

Rp( f - R(2 п п - f )) + (1 + R ) p ( y sin( T ₀ + а ) - R sin т ₀) 1 - R ²

Подставляя (10) во второе и четвертое уравнения (9) получим систему двух уравнений относительно т0 и f , которую запишем в виде pacost0 - pbsin т0 = A,

- pccost0 + pd sin т0 =-B, где а = (1 - R)(1 - y cosa) + R/f sin а.

b = f (1 - Rycosa) - (1 - R)ysin a c = (1 - R)(1 - ycosa) + (2nn - f)ysin a d = (2nn - f)(R - ycosa) - (1 - R)Ysin a

A = (1 - R )( e -A k ) + -^- | 2 n nR - ^f (1 + R )² |

(1 + R ) (         2          J

B = (1 - R)( _£ - A k ) + p ^z f- ( (2 n - f )(1 + R ²) - 2 R f ) Используя (11), получим соотношение

V(Ad - bB)2 + (Ac - Ba)2 ц = ГТ/ n , |ad - bc| определяющее в плоскости  ц, f границу существования неподвижных точек, соответствующих основному (с поочередными ударами каждым поршнем о наковальню) периодическому режиму движения.

Устойчивость неподвижной точки определяется, как известно [17], величиной корней характеристического уравнения х ( z ) = 0, который в нашем случае имеет вид

х ⁽ z ) = ^b 11 ^b 22 z ^{2 + ( a}11^b 22 ^{+ a} 22 ^b11 ^{- a} 21 ^b12^{)z + a}11^a 22 ^{- a} 12 ^a 21 .

В (12) введены обозначения

R

an = R(1 + R)pycos(t0 + a) + Rp + -^(x - PYsm(T0 + a))

a ₁₂ = ^- ( ц sin t ₀ - x ),

a21 = (2nn - f) R (jc - py sin(T0 + a))+ (2nn - f)(1 + R)pycos(t0 + a) +

+ (2nn - f)p - /Cj + pysin(T0 + a), a22 = (2nn - ^) у (^ sin т0 - x),

Ь11 = 1(p^ - x + ^/sin(T0 + a)), b12 = ^(x - pc - ^sin т0) - (Rp + (1 + R)^cost0), b22

= xc1 - (2nn - ^)p - ^sinт0.

Периодическое решение устойчиво, если все корни (12) расположены внутри единичного круга, т.е. выполняется неравенство z <  1 . Нарушение условий устойчивости неподвижной точки происходит либо когда абсолютное значение одного из корней характеристического уравнения становится равным z = ± 1 , либо когда z = exp( ± j ϕ ),0 ≤ ϕ ≤ π . Границы области устойчивости рассматриваемого периодического движения, обозначаемые N ₊ , N _- , N _ϕ , удовлетворяют уравнениям χ (1) = 0, χ ( - 1) = 0, χ ( e ^{± j ϕ} ) = 0,0 ≤ ϕ ≤ π .

Кроме того, известно [17], что при непрерывном изменении параметров интересующий нас периодический режим движения исчезает либо из-за нарушений условий устойчивости, либо из-за выхода фазовой траектории из области определения соответствующего точечного преобразования. Выход фазовой траектории из области определения точечного отображения, определяемой бифуркационной поверхностью N , связан с касанием траектории в некоторые моменты времени τ поверхности S (рис.2).

Таким образом, область существования устойчивых периодических движений рассматриваемой системы ограничена поверхностями N ₊ , N _- , N _ϕ и поверхностью

N _C .

Границы области устойчивости N ₊ , N _- , N _ϕ имеют вид

N ₊ :   b ₁₁ b ₂₂ + ( a ₁₁ b ₂₂ + a ₂₂ b ₁₁ - a ₂₁ b ₁₂) + ( a ₁₁ a ₂₂ - a ₁₂ a ₂₁) = 0,

N _- :   b ₁₁ b ₂₂ - ( a ₁₁ b ₂₂ + a ₂₂ b ₁₁ - a ₂₁ b ₁₂) + ( a ₁₁ a ₂₂ - a ₁₂ a ₂₁) = 0,

N _ϕ : b ₁₁ b ₂₂ - ( a ₁₁ a ₂₂ - a ₁₂ a ₂₁ ) = 0.

Визуализация и анализ результатов вычислительных экспериментов

Исследование сложной динамики двухпоршневого механизма проведено с помощью численных расчетов с использованием программного комплекса, разработанного в среде Borland Developer Studio 2006 [18 - 20]. Данный комплекс позволяет проводить расчеты фазовых траекторий, бифуркационных диаграмм и областей устойчивости основных режимов движения в пространстве параметров механизма.

Обозначим через D ( m , m ) область существования устойчивых периодических движений в пространстве параметров, где m - число ударов первым поршнем о шабот, m ₂ - число ударов вторым поршнем о шабот.

На рис.3 в плоскости (p, R) представлена область D(1,1) (заштрихованная область) для значений параметров γ = 4,ϕ = 0.52, µ = 0.1, k = 0,∆k = 0 и различных значений Е (расстояние от точки крепления шатуна до нижнего основания ПУ). На рис.3а е = 0.02, на рис.Зб е = 0.15.

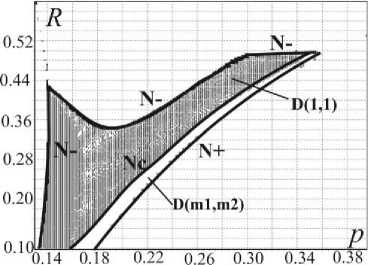
а)

Рис.3. Область D(1,1) существования устойчивых периодических движений в

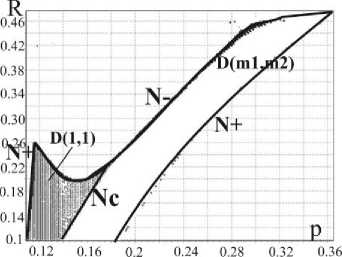
б)

плоскости ( p , R ) при различных значениях е .

Бифуркационная граница N [17] существования точечного отображения (11) отсекает из области устойчивости, ограниченную поверхностями N ₊, N_ , небольшую часть D ( m_x , m ₂), где т_х и m₂ не равны одновременно 1.

Сравнивая рис.3а и 3б можно увидеть, что увеличение параметра Е (расстояние от точки крепления шатуна до нижнего основания ПУ) приводит к уменьшению размеров области существования устойчивых периодических режимов движения механизма и смещению области периодических режимов в сторону уменьшения значений частотного параметра p .

На рис. 4, 5 изображены бифуркационные диаграммы, построенные для того же набора параметров, что и рис. 3а,б соответственно, но при R = 0.22 . На диаграмме на оси абсцисс приведены значения частотного параметра p , а по оси ординат –

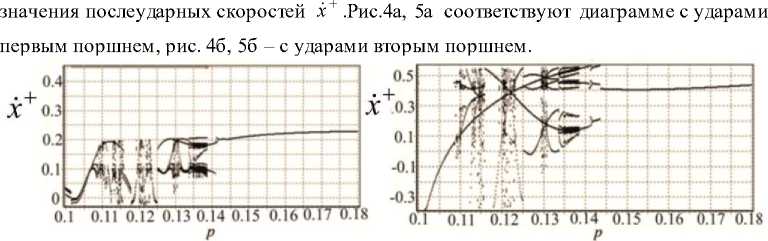
Рис.4. Бифуркационные диаграммы по частотному параметру p для значений

параметров R = 0.22, е = 0.02, у = 4, ф = 0.52, ц = 0.1, к = 0, А к = 0 .

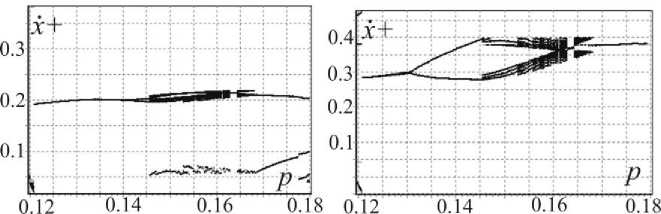
• а)                                            б)

Рис.5. Бифуркационные диаграммы по частотному параметру p для значений параметров R = 0.22, ε = 0.15, γ = 4, ϕ = 0.52, µ = 0.1, k = 0, ∆ k = 0 .

Из рис. 4, 5 видно, что увеличение ε приводит к смещению области периодических режимов в сторону уменьшения значений частотного параметра p так, на рис.4 основной периодический режим движения наблюдается при 0.145 ≤ p ≤ 0.18 , а на рис.5 при 0.121 ≤ p ≤ 0.13 .

На рис.6 а,б в плоскости (p,R) представлена область D(1,1) значений параметров ε = 0.02,γ = 4,µ= 0.1,k = 0,∆k = 0 и различных значений угла ϕ , на рис.6a ϕ= 0.3, на рис.6б ϕ= 3

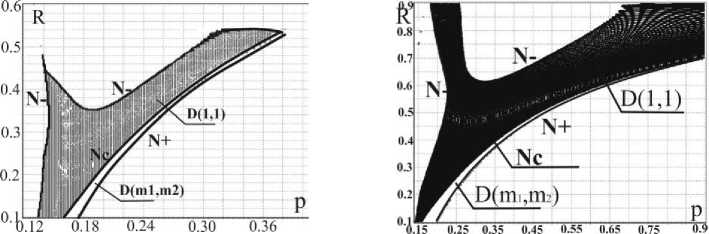
а)                                                б)

Рис.6 Область D(1,1) существования и устойчивости периодических движений в плоскости ( p , R ) для различных значений ϕ

На рис.7, 8 представлены бифуркационные диаграммы по частотному параметру p при том же наборе параметров, что и рис.8а,б соответственно, но при

R = 0.3.

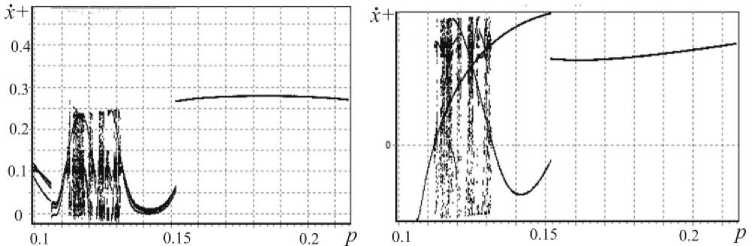
а)

б)

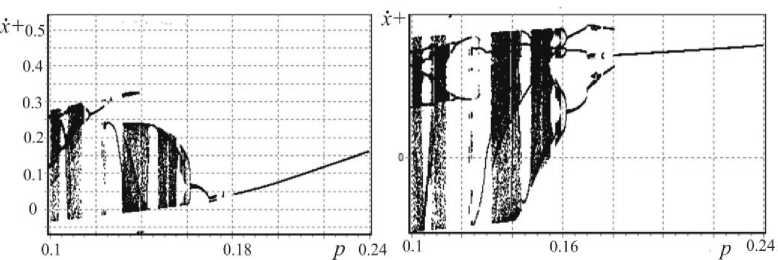
Рис.7. Бифуркационные диаграммы по частотному параметру p для ϕ = 0.3

а)                                    б)

Рис.8. Бифуркационные диаграммы по частотному параметру p для ϕ = 3

На рис.7 основной режим ( m = 1, m = 1 ) наблюдается в интервале 0.15 ≤ p ≤ 0.215, при 0.12 ≤ p ≤ 0.13наблюдается хаотический режим.

На рис.8 для 0.18 ≤ p ≤ 0.24 существует основной режим m = 1, m = 1 , при 0.1 ≤ p ≤ 0.12 и 0.122 ≤ p ≤ 0.16 , наблюдается хаотический режим.

Анализ представленных областей устойчивости и бифуркационных диаграмм показал, что увеличение ϕ (сдвига по фазе между эксцентриситетами) приводит к увеличению областей существования устойчивых периодических режимов, т.е. интервала значений частотного параметра p , при которых существуют периодические движения, становится шире.

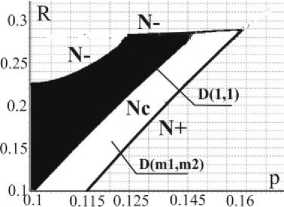
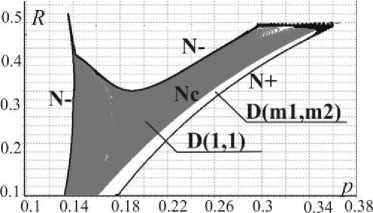
На рис.9 в плоскости ( p , R ) представлена область D (1,1) для набора параметров ε = 0.02, γ = 2.5, ϕ = 0.52, µ = 0.1, k = 0, ∆ k = 0 , и различных значений γ = 2.5 (рис.9а) γ = 4(ри.9б).

• а)                                    б)

0.1       0.11     0.12     0.13      0.1       0.11      0.12      0.13 '

Рис.9. Область D(1,1) существования устойчивых периодических движений в плоскости ( p , R ) для различных значений параметра γ .

На рис.10,11, построенных для того же набора параметров, что и рис.9, представлены бифуркационные диаграммы для R = 0.25 .

На рис.10 основной режим с m = 1, m = 1 существует для 0.116 ≤ p ≤ 0.125 , для 0.112 ≤ p ≤ 0.116 m1 = 2, m2 = 2 , p = 0.116  - бифуркационное значение параметра, при 0.104 ≤ p ≤ 0.112 наблюдается хаотический режим, при 0.1 ≤ p ≤ 0.104 m1 = 2, m2 = 2 .

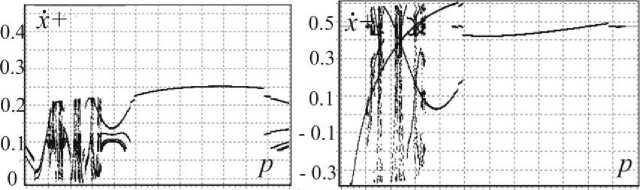
На рис.11 основной режим наблюдается при 0.15 ≤ p ≤ 0.21 , при 0.13 ≤ p ≤ 0.15 m ₁ = 3, m ₂ = 2 , при 0.21 ≤ p ≤ 0.22 m ₁ = 4, m ₂ = 1 , хаотический режим существует при 0.1 ≤ p ≤ 0.13 .

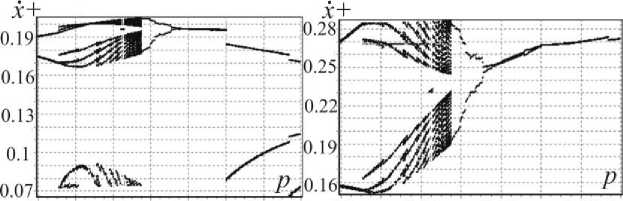
Рис.10. Бифуркационные диаграммы по частотному параметру p для у = 2.5

0.1     0.13 0.16 0.19 0.22 0.1    0.13    0.16    0.19    0.22

Рис.11. Бифуркационные диаграммы по частотному параметру p для у = 4

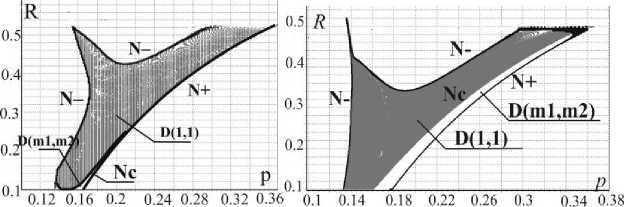
На рис.12 представлена область устойчивости в плоскости параметров ( p , R )

, где ц = 0.1, е = 0.02, у = 4, ф = 0,52, Х _х = 0, Х 2 = 0, к 1 = 0.1,Л к = 0.1, но на рис.12а к = 0, Л к = 0 (не учитываются высоты наковален), на рис.12б к_х = 0.1, Л к = 0.1 (высоты наковален учитываются).

а)                                                  б)

Рис.12. Области D(1,1) существования и устойчивости периодических движений в плоскости ( p , R ) для различных значений параметров к_х , Л к

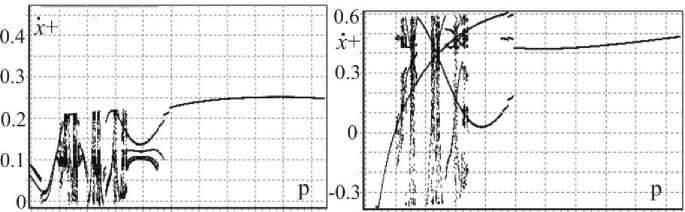
А на рис.13,14 представлены бифуркационные диаграммы для того же набора параметров, что и рис.12а,б, но для R = 0.25 .

0.1              0.15             0.2 0.1               0.15             0.2

а)                                       б)

Рис.13. Бифуркационные диаграммы по частотному параметру p для к = 0, Лк = 0

0.1           0.14         0.18 o.l            0.14          0.18

• а)                                       б)

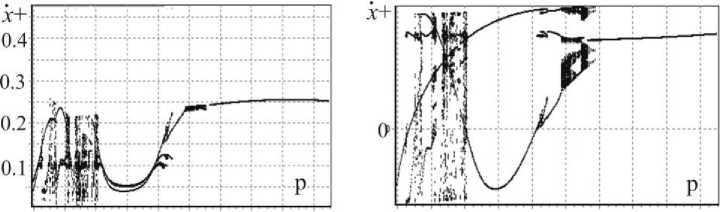
Рис.14. Бифуркационные диаграммы по частотному параметру p для k=0.1,∆k=0.1

Анализ представленных диаграмм и областей устойчивости показал, что учет высот подставок наковален k , k + ∆ k приводит к изменению конфигурации области существования периодических режимов движения. Так на рис.13 видно, что периодический режим для выбранных значений параметров существует при 0.15 ≤ p ≤ 0.205 (без учета высот наковален), а на рис.14 периодический режим существует при 0.16 ≤ p ≤ 0.195 .

Проведенные численные эксперименты позволили сделать вывод о том, что наиболее существенно влияют на динамику механизма параметры ε , ϕ , k , ∆ k .

Заключение

Информационные технологии начинают играть все более важную роль не только как инструмент автоматизации образовательного процесса, но и как отличный полигон для проверки получаемых знаний. Применение информационных технологий в образовании позволит добиться повышения эффективности и качества процесса обучения, и интенсификации процесса научных исследований в образовательных учреждениях;