Использование тензорной методологии анализа систем для описания бизнес-процессов предприятия. Средства автоматизации

М. H. Петров, H. Г. Треногин, Е. А. Веловатый

ИСПОЛЬЗОВАНИЕ ТЕНЗОРНОЙ МЕТОДОЛОГИИ АНАЛИЗА СИСТЕМ ДЛЯ ОПИСАНИЯ БИЗНЕС-ПРОЦЕССОВ ПРЕДПРИЯТИЯ.

СРЕДСТВА АВТОМАТИЗАЦИИ

Рассмотрены основные аспекты применения для анализа систем тензорнойметодологии, позволяющейупрос-тить задачу описания и анализа. В качестве примера описан бизнес-процесс современного предприятия. Показано применение программного средства для оценки построенной ранее модели.

Развитие производства, науки и техники приводит к созданию все более и более сложных систем. Огромных масштабов достигли технологические комплексы, информационные системы, вычислительные комплексы, банки данных, системы управления.

С ростом сложности систем возникают две основные проблемы:

• -    из-за масштабов трудно производить действия с такими системами (расчет характеристик, проектирование, управление), предвидеть последствия тех или иных изменений, оптимизировать их работу. Для полного описания и моделирования существующих сетей недостаточно мощностей современных вычислительных систем. При этом количественный рост систем порождает и качественные изменения их характеристик;

• -    исследование и создание каждой сложной системы требует больших затрат ресурсов, привлечения больших коллективов разработчиков.

Использование достигнутых результатов в новых разработках стало практически невозможным, поскольку разнообразие природы и типов сложных систем сделало их несопоставимыми, уникальными. Для каждой системы разрабатываются свои методы исследований и рас четов. Однако с ростом сложности систем растет роль характеристик, которые во многом являются общими для различных систем. Это позволяет получать и использовать аналогии между системами различной природы.

Главной проблемой анализа сложных систем является необходимость разработки единого способа представления и описания физических, технических, экономических и других сложных систем. Процесс объединения описаний разнородных систем состоит из следующих этапов:

• -    выделения наименьшей части системы, в которой еще продолжает в полной мере происходить характеризующий эту систему процесс, т. е. элемента системы;

• -    представления системы как совокупности элементов, соединенных друг с другом. Эта совокупность связей с их характеристиками образует структуру системы.

В данной статье для описания сложных систем предлагается использовать тензорную методологию, которая позволяет представить систему в виде, удобном для дальнейшего анализа набора величин.

Понятие тензорной методологии анализа систем. Процесс описания разнородных систем с помощью универсальных понятий элемента и структуры создает предпосылки для следующего обобщения: множество систем является множеством различных проявлений некоторой обобщенной абстрактной системы, а следовательно, элементы и структуры исследуемых систем определенным образом взаимосвязаны друг с другом. В таком случае, имея результаты анализа одной системы, можно прикладывать их к другим системам с помощью некоторого количества стандартных преобразований, как это делается в геометрии при изменении системы координат. Тогда имеет смысл рассматривать обобщенную абстрактную сложную систему как геометрический объект, помещенный в некоторое многомерное пространство, а все многообразие существующих систем - как проекции данного объекта в частные системы координат.

Теория преобразований систем координат изучается в рамках векторного исчисления. Математическим аппаратом, позволяющим оперировать обобщенными и-мерными пространствами и объектами в них, является тензорный анализ, обобщающий векторное исчисление и матричную алгебру.

Рассматривая обобщенную абстрактную систему как тензор, а множество подлежащих анализу сложных систем - как проекции этого тензора, можно, используя результаты исследования и расчета одной системы, получать результаты для других систем.

Автором тензорной методологии анализа систем является американский ученый и инженер Г. Крон [1; 2]. Он использовал тензорный анализ в приложении к теории электрических сетей и сделал вывод, что инвариантом преобразований структуры является линейная форма, связанная с каждым элементом сети.

В приложении к теории связи тензорная методология Г. Крона свое дальнейшее развитие получила в работах [3; 4], в которых тензорная методология была впервые использована для анализа вероятностно-временных характеристик в сетях связи.

Контурный метод анализа сети. При рассмотрении сети из к контуров в качестве переменных принимаются величины, характеризующие интенсивности потоков, протекающих в контурах сети (это могут быть потоки энергии, потоки вызовов и т. д.). Такие потоки называются контурными. Контурные потоки не имеют явного физического смысла и приобретают его, суммируясь в ветви, по которой они протекают При этом сумма всех контурных потоков, протекающих в данной ветви, с учетом их направлений образует поток в данной ветви, который имеет физический смысл и является измеряемой величиной.

Для сетевых задач в качестве исходной системы координат принимается структура исходной сети, подлежащей анализу Вспомогательная система координат определяется как структура той же размерности, что и исходная сеть, элементы которой (ветви, подсети, произвольные структурные блоки) соединены неким другим способом. Из множества вспомогательных сетей выделяется так называемая примитивная сеть - сеть, состоящая из и не соединенных между собой ветвей - элементов.

Как показал Г. Крон, для любой контурной сети примитивная сеть состоит из и отдельных ветвей, каждая из которых короткозамкнута на себя (рис. 1).

Таким образом, примитивная и-мерная сеть представляет собой множество и отдельных ветвей, содержащих

элементы сети без каких-либо непосредственных соединений между ними (с помощью узлов). Однако некоторые или все элементы сети в ветвях могут влиять друг на друга косвенно, например используя общий ресурс оперативной памяти или процессорного времени узла коммутации ит.д.

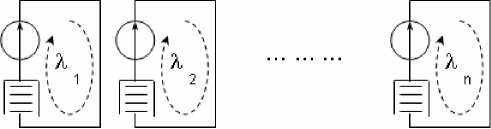
Рис. 1. Примитивная и -мерная контурная сеть

Если применять данный подход к теории массового обслуживания, то уравнение состояния примитивного элемента представляет собой формулу Литтла:

N= Т-Х,

где Т- время задержки передачи сообщения в узле коммутации, с; N - объем буфера узла коммутации; Х - интенсивность поступления сообщений, эрл.

Эти величины могут быть переходными или установившимися, функциями времени, линейными операторами и т. д.

Геометрические объекты, а также уравнение состояния примитивной сети, выраженное в терминах этих геометрических объектов, записанные в матричной форме, имеют тот же вид, что и для элемента этой сети:

• -    Х - вектор, компоненты которого представляют собой интенсивности потоков сообщений, протекающих в соответствующих ветвях;

• - N- вектор, компоненты которого представляют собой объемы буферов систем массового обслуживания в соответствующих ветвях;

• -    Т - квадратная матрица размерностью и строк на и столбцов. Элементы ее главной диагонали представляют собой значения времени задержки в системе массового обслуживания, соответствующей данной ветви. Ос

тальные элементы матрицы отражают взаимное влияние систем массового обслуживания друг на друга (использование общих ресурсов и т. д.).

Геометрические объекты, описывающие примитивную сеть, могут быть представлены в следующем виде:

N

N 1         λ 1

N 2        λ 2

, Х =

Т=

N n

λ n

д

T

T

И

т „ т

1,2 ...      1,

Т      гр

2,2   ...     2,

т

T n ,2

...

T n , n

Инвариантное матричное уравнение состояния примитивной сети

N=T-X                    (1)

эквивалентно системе и обычных уравнений:

^N 1 - ^Т 1,1 ■ ^Х 1 ^{+ Т} 1,2 ■ ^Х 2⁺ - ^{+ Т} 1,„ ■ ^Х „^,

^N 2 - ^Т 2,1 ■ ^Х 1 ^{+ Т} 2,2 ■ ^Х 2⁺ - ^{+ Т} 2,„ ■ ^Х „^,          ( ² )

\'     Т 'Л ' Т 'Л ' ... ■ Т 'Л.

Геометрические объекты, необходимые для описания исходной сети, и уравнения состояния исходной сети, выраженные в матричной форме, имеют тот же вид, что и для примитивной (вспомогательной) сети, отличаясь лишь значениями компонент.

Геометрический объект, связывающий переменные обеих систем, называется тензором преобразования. Так как переменными (величинами отклика) в контурных сетях являются интенсивности потоков сообщений, то уравнение преобразования принимает вид

Х -С- Х' , (3) где X - вектор интенсивности поступления сообщений для примитивной (вспомогательной) сети; X' - вектор интенсивности поступления сообщений для исходной сети; С - матрица преобразования интенсивностей между примитивной и вспомогательной сетями.

Получим выражение интенсивностей потоков ветвей примитивной сети через интенсивности контурных потоков исходной сети:

Х1 = С1,1 ' X' 1 + С1,2 ' Х' 2 ' — ' С. . ' Х' ., x c -х' ■ c -х' ■ ^ ■ c -х' (4)

^Х и ^{- С} и. 1 ' ^Х' 1 ^{+ С} 2,2 ^{- Х}' 2 ⁺ - ^{+ С} и, i ^{- X}' Р матрицу тензора преобразования:

C = C11 C2,1 ... с 1,2 с C2,2 ... ...        1,k ...   C2,k ...      ... ,                (5) . Cn ,1 Cn,2 ...   Cn,k J N (СТ)-1 ■N'; (6) матрицу значений времени задержки в исходной сети

Т'=С^Г-Т-С.               (7)

Компоненты матрицы времен задержек Т' исходной сети находятся по компонентам матрицы Т примитивной сети с помощью формулы преобразования (7) умножением Т на транспонированную и прямую матрицы тензора преобразования С.

Система уравнений состояния исходной сети в матричной форме имеет вид

N-T'-X',(8)

v=c-X',(9)

Ne=T-C-X'.(10)

Решение данной системы можно получить любым методом теории систем линейных уравнений и матричной алгебры. Результатом ее решения является вектор интенсивностей контурных потоков сообщений. В случае если вспомогательная сеть является примитивной и-контурной сеть, интенсивности поступления вызовов в отдельных ветвях исходной сети находятся по формуле (9). Объемы буферов систем массового обслуживания в отдельных ветвях находят по формуле (10).

В простой сети малой размерности, без взаимных влияний элементов сети, уравнения состояния легче и быстрее получить простым рассмотрением структуры сети и аналитическими методами. Однако при усложнении сети эта задача будет очень сложной.

Использование тензорной методологии на примере описания бизнес-процесса предприятия. Рассматриваемый авторами подход дает значительное упрощение задачи описания и анализа не только сетей массового обслуживания при моделировании информационных систем, но и других задач из многих областей [5-7].

В качестве примера рассмотрим описание бизнес-процессов согласования и предоставления широкополосного доступа в Интернет физическим лицам в Новосибирском филиале ОАО «Сибирьтелеком» (рис. 2):

• - 1,5- заявка на предоставление доступа поступает от клиента сотруднику подразделения «Телекомсервис» посредством заявления (1) или путем устной заявки по телефону 061 (5). Отделом продаж новых услуг структурного подразделения «Телекомсервис» производится проверка технической возможности предоставления услуги;

• - 13,14 - в случае отсутствия технической возможности формируется отрицательный ответ клиенту с указанием причины отказа;

• -    2, 6 - в случае наличия технической возможности клиентом оформляется и подписывается бланк-заказ и договор на оказание услуги;

• -    9,11 - формируется комплект документов на предоставление услуги для передачи клиенту;

• - 3,7- специалист отдел продаж новых услуг структурного подразделения «Телекомсервис» вносит заявку на подключение в автоматизированную систему расчетов, выписывает наряд в кросс. Выполняются кроссиро-вочные работы и производится активация порта;

• -    4, 8 - электромонтер линейного цеха технического центра телекоммуникаций выезжает к абоненту и выполняет работы по инсталляции оконечного оборудования;

• - 10, 12 - клиенту поступает отказ или подписанный договор на предоставление услуги.

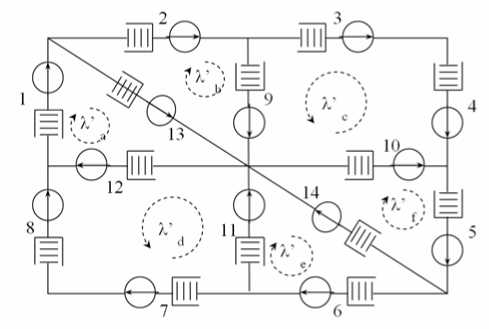
Рис. 2. Бизнес-процесс согласования и предоставления широкополосного доступа в Интернет

С использованием тензорной методологии данная система может быть описана следующим образом:

X X 2

...

Х 14

C

T

N =

N ₁

N ₂

N

14 ,

T1,1     0    ...0

0   T2,2   ...0

...       ...     ......

0     0    ...   T 14,14

C =

01 0 0

- 1

- 1

0 - 1

- 1

грамму «Тензор» как средство автоматизации описания систем с применением тензорной методологии (рис. 4).

- 10 0

- 10 0

0 - 1 1

001 1

000 01

- 1

- 1

- 1

01 0 00

- 1

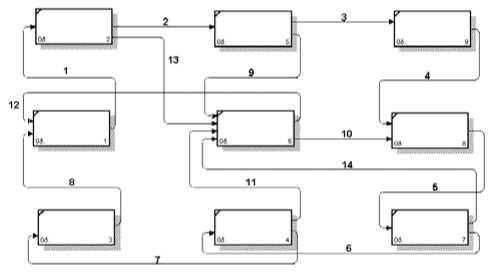
Рис. 3. Схема бизнес-процесса в программе BPWin

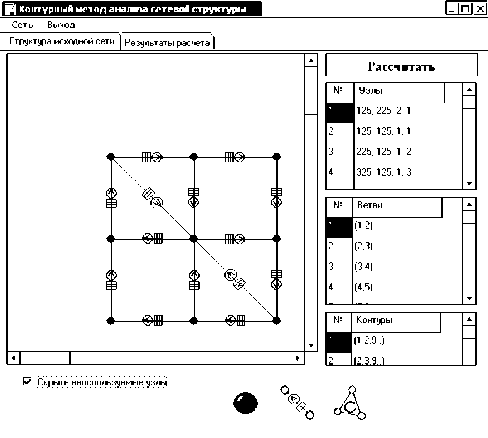
Рис. 4. Внешний вид программы «Тензор» для бизнес-процесса согласования договоров

С учетом формул (6), (7), (8) это описание приобретет ВИД

N 1 ⁺ N 12 ⁺ N 13 = ⁽ T 1,1 ⁺ T 12,12 ⁺ T 13.13 ^{) Х} a ^- T 13,13 ^ b ⁺ T 12,12 ^ d ’

N 2 ⁺ N 9 ^- N 13 = - T 13.1Л a ^{+ (} T 2,2 ⁺ T 9,9 ⁺ T 13,13 ^{) Х} b ⁺ T ^Л c ’

_-N 3 - N 4 + N 9 + N10 = T 9,9Хb + (T 3,3 + T 4,4 + T 9,9 + T 10.10)Хc + T 10,10^ f, - N 7 - N 8 + N11 + N12 = T 12,12^ a + (T 7,7 + T 8,8 + T 11,11 + T 12,12^ d + T 11.1Л 4 ’ N 6 + N11 - N14 = T 11.1Лd + (T 6,6 + T 11,11 + T 14,14)^4 - T 14,14^f, _N5 + N10 + N14 = T 10,10^c - T 14,14^4 + (T 5,5 + T 10,10 + T 14,14)^ f ’ т е. мы получили систему уравнений, соответствующую формуле (8). Так же могут быть получены системы для формул (9) и (10).

Приведенный выше пример не является очень сложным. Существующие бизнес-процессы могут иметь намного более сложную структуру с бьльшим количеством элементов.

Использование средств автоматизации расчета параметров. Для наглядного отображения систем часто используют специализированные программные средства, например программный пакет BPWin (рис. 3).

Для упрощения задачи анализа авторы предлагают использовать специализированную компьютерную про

Эта программа имеет пользовательский интерфейс для составления схемы системы. Необходимо лишь определить узлы сети, ветви и указать контуры. После окончания составления схемы нужно нажать кнопку «Рассчитать», и программа сформирует все параметры описания системы.

Помимо ручного составления схемы, программа имеет механизм загрузки схем из файлов пакета BPWin.

Результаты расчета параметров с помощью программы «Тензор» соответствуют полученным нами ранее без использования этой программы.

Тензорная методология является мощным инструментом для исследования характеристик сложных систем. Универсальность и общность описаний и рассуждений создает предпосылки для широкого применения этой методологии в современных условиях.

Представленный выше подход по использованию тензорной методологии для описания сложных процессов и систем на примере бизнес-процесса организации позволяет в полной мере описать систему и происходящие в ней изменения. Использование средств автоматизации позволяет значительно упростить рутинные операции вычисления параметров, учитывая тот факт, что многие си- стемы имеют очень сложную структуру с большим количеством элементов.