Использование ультразвуковых концентраторов резонансной длины в нанотехнологии

Известно, что ультразвук является эффективным средством воздействия на многие технологические процессы. Особое внимание здесь следует обратить на явление акустической кавитации. Обработка жидкостей в режиме кавитации способствует ее активации, изменяет ее физико-химические свойства, интенсифицирует химико-технологические процессы [1]. Исследования акустической кавитации приобретают актуальность в связи с развитием нанотехнологий [2-6]. Известно, что наночастицы часто образуют агломераты. Для эффективного использования нанопорошков в технологиях получения новых материалов требуется решить минимум две задачи:

• 1)    разбить агломераты наночастиц;

• 2)    распределить наночастицы равномерно в объеме основного материала.

Эти задачи хорошо решаются методом ультразвукового диспергирования [79]. Еще больший эффект достигается при использовании ультразвука в режиме акустической кавитации. Известно, что для создания эффекта акустической кавитации необходимо три составляющих:

• 1)    генератор ультразвуковых колебаний;

• 2)    преобразующее устройство, зачастую это магнитострикционный преобразователь;

• 3)    волновод — излучатель, который во многих исследованиях называют “концентратор”, подчеркивая этим названием его особую роль (здесь и далее мы

будем использовать последнее название этого элемента ультразвуковой техники [10].

Концентраторы классифицируются по принципу действия на фокусирующие и стержневые [11]. «Стержневой концентратор» применяют для увеличения амплитуды колебательного смещения частиц (колебательной скорости частиц). Вызывают интерес такие концентраторы, которые могут создавать максимальный объем кавитирующей жидкости. При этом повышается эффективность практического использования ультразвука в режиме акустической кавитации. Актуальным становится правильный выбор формы и размеров концентратора.

Расчет концентратора можно провести с помощью волнового уравнения, составленного для стержневых концентраторов с использованием теории и функции комплексного переменного

Для того чтобы эффективно использовать энергию ультразвуковых колебаний для дисперсии нанопорошков, необходимо правильно вычислить геометрические параметры концентратора.

Основные уравнения

Введем три предположения, чтобы получить волновое уравнение для концентраторов:

• 1.    Фронт волны напряжения, распространяющейся вдоль оси концентратора, плоский.

• 2.    Напряжения, возникающие в концентраторе, равномерно распределены по поперечному сечению.

• 3.    Продольные деформации в концентраторе упругие.

Теоретический расчет на основании преобразования и решения волнового уравнения приведен полностью в [12].

При выполнении первых двух условий в концентраторе распространяется продольная мода колебаний, при этом диаметр концентратора меньше или равен половине длины волны звуковых колебаний

D ≤ λ ,                             (1)

где D — диаметр концентратора; λ — длина волны.

Третье условие выполняется при σ m < σ 02 . Здесь σ m — амплитудное значение напряжений в концентраторе, σ 02 — условный предел упругости материала концентратора. Третье условие исключает нагрев концентратора, что особенно важно при использовании их в процессах химической, биохимической, пищевой, лесохимической и других технологиях, связанных с переработкой термолабильных материалов.

При таких допущениях бесконечно малое смещение u поперечного сечения S концентратора в направлении координаты х связано с относительным удлинением ∂ ^u (деформацией) следующим выражением:

∂x du= udx                      (2)

∂ x

Тогда сила упругости, вызывающая это смещение, будет пропорциональна произведению относительного удлинения на площадь поперечного сечения:

F =- ES ∂ ^u                     (3)

∂x где Е — модуль Юнга материала концентратора.

В свою очередь, дифференциальное уравнение движения единичного объема материала концентратора можно записать следующим образом:

• d V _ _— 1 d F d t    p S d x

  
  

где V — колебательная скорость поперечного сечения концентратора; p — плот- ность материала концентратора; t — время.

Таким образом, из выражения (3) легко получить основное дифференциальное уравнение, описывающее совместно с (4) изменение силы упругости и колебательной скорости в концентраторе:

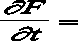
— ES

Учитывая гармонический характер колебаний, можно представить выражение для силы упругости и колебательной скорости следующим образом

F = F m sin( a t + ф р )

V = V m sin( a t + ф у ).

В комплексной форме

■

F ^ F e^j""

■ где y_ — у eJVv — комплекс эффективной колебательной скорости;

2 m e

_JF _ ^—F ejPF — комплекс эффективной колебательной силы.

Дифференциальные уравнения (4) и (5) в комплексной форме принимают вид:

■

■

1 dF

—

V _---- jropS dx

—

•

.

„ ES dV

^{F _} ™ j< » dx

Анализ волнового процесса продольно возбуждаемых концентраторов с помощью полученных уравнений значительно упрощается. Это объясняется тем, что представление синусоидальных функций в комплексной форме исключает переменную t , а введение третьего допущения обусловливает отсутствие активных потерь в концентраторе, что не будет вызывать в нем затухания волн.

Площадь поперечного сечения концентратора в общем случае зависит от координаты х , продифференцировав выражение (6) по х , получим:

—

dF dx2

■ Л

,, dS    div

_ jtop Vdx + ^dx

k

У

•

■

Подставляя в последнее выражение значения V и dVиз (6) и (7), получим dx волновое уравнение концентратора в комплексной форме:

■

■

d 2 F  S ' dF

dx2  S dx

■

+ k 2 F _ 0 ,

где                    — волновое число;

, ro  2nf 2nf к = - = -- = —;= cc E

S = dS s = _n R 2 - площадь поперечного сечения концентратора. dx’

С учетом последних соотношений уравнение (9) можно переписать в следующем виде:

d2F dx2

2R dF

R dx

•

+ k²F =

здесь ^dR

R _dx

Аналогично можно получить волновое уравнение концентратора в комплексной форме относительно колебательной скорости:

•

•

d² V 2R dV , ₂ •

--. +       + k² V = 0

dx2   R dx

Расчет концентраторов сводится к определению его резонансной длины по-

средством решения уравнения (10) или (11) при следующих граничных условиях:

•

V '(0 ) =

•

V ' ( e ) = 0

•

V ' ( 0 ) = V

Концентратор, рассчитанный с учетом условия (12), будет резонансным и присоединение его к электромеханическому преобразователю не изменит режима работы последнего, т.е. будет удовлетворяться и условие (13).

Для уточнения порядка расчета концентраторов выявим семейство образующих R(х) , при котором волновое уравнение в комплексной форме (11) имеет аналитическое решение.

Для этого комплекс колебательной скорости представим следующим образом

•

V = u ( ^{x )} , подставим в уравнение (11) и приведем его к каноническому виду:

- R ⁽ X)

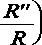
• и = 0

d²u dx²

+ k2

При такой замене граничные условия (12) и (13) принимают следующий вид:

iu ( o ) = V ^' C 0 ) R ' ,	(15)
u ( e ) = V*(eX Re ’	(16)
u ( 0 ) = V o R 0 "	(17)

Уравнение (14) при соблюдении следующего условия k - R- = к’2 = const > 0,                 (18)

имеет решение и= .4sin kx + ф) ,                        (19)

где A и ф — постоянные интегрирования; к' — волновое число, учитывающее дисперсию фазовой скорости в концентраторе.

Функций, удовлетворяющих условию (18), всего три. Они характеризуются

R "

тем, что отношение для них постоянно, это:

R

• 1)    R(x) = a x + b — прямая линия. Причем, если

а # 0 — то концентратор конический;

а = 0 — то концентратор цилиндрический;

• 2)    R(x) = a e^{- в} x + b e ^e x — цепная линия, при:

в = 0 — экспоненциальный концентратор;

а = в — катеноидальный концентратор;

• 3)    R(x) =a cos ( в x + ф о ) — тригонометрические кривые, при этом профиль концентратора имеет гантелевидную форму.

Постоянные интегрирования определяются из граничных условий (15 — 17):

A sin ф =

V 0 R 0 ,

A к соз ф = V 0 R 0 ^,

отсюда

( R 0

= arctg ^ к R )

+ nn ,

ф

A =

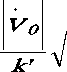
R o ²

+ ( к R 0 ) ²

k

к

Следовательно, выражение (2.19) примет вид:

u (x )

V 0 R 0 .

k "              (

= — 0rRs sin I k x + arctg

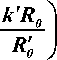
Для определения резонансной длины концентратора используем граничное условие на выходе концентратора

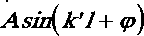
u 1 R₁ ,

к AcoS ( к l + ф ) =

u i R 1 .

R

Отсюда tdkl+ mA — к R¹ и, учитывая, что tgф = к —0 , получим: ^gg„ + ^ф-  R1                    R 0

tgk' l =

R o   R 1

^Ro  ^R1 )

R o R 1

R 0 R 1

+ к²

Выражение (27) позволяет определить резонансную длину вышеперечислен- ных концентраторов.

Теоретическая часть

Рассчитаем резонансную длину простейшего цилиндрического концентратора.

• 1.    Для концентраторов, радиус которых изменяется по линейному закону (образующая концентратора — прямая линия):

R(x) = a x + b, здесь R'(x) = a и k'= k; тогда r(x) = 1-

—

l

R

0 X x + R₀ и, введя соотношение вход-

ного радиуса поперечного сечения концентратора к выходному n = R o , имеем:

R1

tgk =

kl

N ( kll ) 2 ( - - N ) ²

.

При N = 1 , или при равенстве входного и выходного радиуса R o = R 1 цилиндр, и его резонансная длина равна:

имеем

n n l = k

.

где n = 1, 2, 3, ..

В основном концентраторы изготавливаются из титановых сплавоы. В

нашем

случае марка ВТЗ-1. Модуль упругости для него (Модуль Юнга) Е = 1.15×10¹¹ Пa и плотность ρ = 4500 кг/m³ . Частота ультразвуковых колебаний генератора f = 23,000 ± 1,000 кГц , коэффициент Пуассона р = 0,3.

Тогда волновое число получается:

k =   ^{2 n f} * 28.57

Резонансная длина концентратора при n = 1 соответственно равна

ПП l =---* 0.11 м .

k

Волновые уравнения для колебательной силы и скорости (10) и (11) имеют приближенных характер, но они хорошо отражают физику явления. При выводе этих уравнений не учитывали радиальные деформации концентратора. Известно, что между продольной и радиальной деформацией существует связь через коэффициент р . Для металлов его величина лежит в пределах от 0,25 до 0,35. Впервые методику вычисления резонансной длины стержня постоянного сечения при наличии радиальных деформаций дал Рэлей [13]. При этом получилось, что резонансная длина уменьшается на величину, равную:

Л 2 2 П | R |Л = п и. — — ^ n р 4^ i)

,

где n = 1, 2, 3,

..

., Δ — относительное изменение размера.

Для n = 1 при отношении R к l равном ≈ 0.2 поправка Рэлея составляет ≈ 3∙10³ . Тогда длина концентратора с учетом поправки:

l = —(1 - Л) * 0.11(1 - 0.003) * 0.10967m .k

Видно, что поправка Рэлея в нашем случае незначительна.

Однако, формулу (30) следует учитывать, если увеличить радиус концентратора. При этом поправка Рэлея возрастает.

На рис. 1 представлен волновод, который был использован в наших исследованиях. Проведенные эксперименты показали, что максимальный эффект кавитации достигается при следующих частотах:

• 1)    для водной суспензии наноразмерного диоксида кремния ≈ 23277 Гц;

• 2)    для базового моторного масла с наноразмерным порошком меди ≈ 22900 Гц.

Рис. 1. Концентратор ультразвуковых колебаний резонансной длины

Экспериментальная часть

Также были проведены эксперименты без кавитации для водной суспензии наноразмерного диоксида кремния. Частота, при которой кавитация отсутствовала, составила ≈ 23923 Гц. По результатам исследований получен патент на изобретение [14].

Для достижения максимального эффекта режима кавитации в реальных условиях эксперимента проводилась корректировка частоты генератора ультразвуковых колебаний. Отклонение экспериментальных резонансных частот, от принятой в расчетах (23000 Гц), составляет не более ±500 Гц. Это примерно 3%.

Экспериментальные образцы суспензии были исследованы с помощью спектрофотометра СФ-56 на степень пропускания света определенной частоты. Их сравнивали с эталонными жидкостями. В качестве эталонных жидкостей использовали воду для наноразмерной суспензии диоксида кремния и базовое моторное масло для медных наноразмерных порошков соответственно.

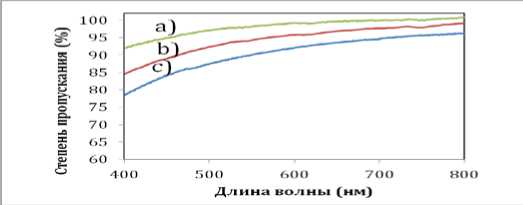
Рис. 2. График пропускания света в % в образцах при различной обработке суспензий наноразмерного диоксида кремния: а) простое перемешивание;

b) воздействие ультразвука; с) воздействие акустической кавитации.

На рис. 2 представлен график степени пропускания света в трех образцах суспензии наноразмерного порошка диоксида кремния. Нижняя линия соответствует образцу, полученному при воздействии кавитации. Верхнюю линию дал образец, полученный механическим перемешиванием (без ультразвука и без кавита- ции). Между ними расположена линия, соответствующая образцу, полученному при воздействии ультразвука без кавитации. Расположение линий на графике говорит о том, что в режиме кавитации диспергирование и деагломерирование частиц наноразмерного порошка кремния эффективнее (свет проходит плохо), чем при простом ультразвуковом воздействии.

На рис. 3 представлен график результатов спектрофотометрических исследований образцов, полученных диспергированием наноразмерного порошка меди в базовом моторном масле.

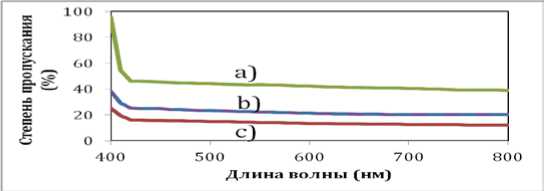
Рис. 3. График пропускания света в % в образцах при различной обработке суспензий наноразмерного порошка меди в моторном масле: а) простое перемешивание; b) воздействие акустической кавитации 1 мин; с) воздействие акустической кавитации 3 мин.

Данные эксперимента показывают, что для достижения высокой эффективности диспергирования время воздействия также имеет значение.

По результатам исследований получен патент на изобретение [14].

Выводы

Из полученных результатов можно сделать следующие выводы:

• 1.    Теоретический анализ волнового процесса в комплексной форме значительно упрощается, так как при этом из синусоидальных функций исключается переменная t — время.

• 2.    Эксперименты подтверждают достоверность полученных расчетных формул с учетом поправок. Эти поправки корректируются частотой ультразвукового генератора в реальных условиях эксперимента.

• 3.    Диспергирование наноразмерных порошков в режиме акустической кавитации более эффективно, чем при воздействии ультразвука без кавитации. Также имеет значение и время воздействия. Это подтверждается приведенными экспериментальными данными.

Работа выполнена при поддержке РФФИ грант №18-02-00523а и БГУ грант №16.8168.2017/БЧ.