Использование вейвлет-преобразования для построения моделей фонем русского языка

При увеличении числа узлов в два раза точность возрастает более чем в десять раз, что подтверждает четвертый порядок сходимости не для всех значений N.

Библиографический список

1. Быкова, Е. Г. Неоднородная разностная схема четвертого порядка точности в области с гладкой границей / Е. Г. Быкова, В. В. Шайдуров // Сиб. журн. вычисл. математики. 1998. Т. 1. № 2. С. 99-117.

Таблица 5

Погрешности задачи (23) в области й_р N = 8

г	10	кг	КК	10 4	К '
А	5,17 ■ Кг	7,56 ■ Кг	7,54 ■ Кг	7,54 ■ Кг	7,54 ■ Кг

Таблица 6

Погрешности задачи (23) в области Q ₁, N = 256

г	10	Кг	КК	10 4	10^5
А	1,21 ■ КК	9,85 ■ Ю '	9,65 ■ К '	9,6 ■ Ю '	9,6 ■ Ю '

Таблица 7

Погрешности задачи (23) в области Ц, г = 10 " ⁵

N	8	16	32	64	128	256	512	1024
А	7,54 ■ Кг	3,18 ■ Кг	7,7 ■ КК	1,2 ■ КК	1,2 ■ Ю 4	9,6 ■ Ю '	6,45 ■ К '	3,79 ■ Ю 9

A DAPTIVE METHODS FOR SOLUTION THE SINGULAR PERTURBED PROBLEMS USING UNHOMOGENEOUS DIFFERENCE SHEMES

Its considered the s^ngular perturbed problems with the small parameter before the highest derivatives. Using the decomposition of the domain its developed the highest order schemes which was suggested in the works V. V. Shaidurov Принята к печати в апреле 2006 г.

ИСПОЛЬЗОВАНИЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ДЛЯ ПОСТРОЕНИЯ МОДЕЛЕЙ ФОНЕМ РУССКОГО ЯЗЫКА

Исследованы возможности использования различных типов вейвлетов для создания моделей фонем русского языка в системе преобразования речи в текст. Показано, что для получения признаков фонем целесообразно использовать кратномасштабное вейвлет-преобразование (базис Добеши 8). Вычисления проводились в среде MatLAB 7.Анализрезультатов показал достаточное качествораспознавания фонем (95 %).

В современных компьютерных системах все больше внимания уделяется построению интерфейса речевого ввода-вывода, поскольку его потенциальная эффективность основана на практически неограниченных возможностях формулировки на естественном языке всевозможных задач в самых различных областях человеческой деятельности. Наиболее перспективными на сегодняшний день являются системы речевого ввода. Но существующие модели понимания речи пока еще значительно уступают речевым способностям человека, что свидетельствует об их недостаточной адекватности и ограничивает применение речевых технологий в промышленности и быту. Известные методы вычисления признаков речевых единиц не позволяют решать реальные задачи, что заставля- ет продолжать исследования в этой области. Кроме того, из имеющихся программных продуктов рынка систем распознавания речи лишь немногие поддерживают русский язык.

При проектировании системы преобразования речи в текст одной из важных задач является выбор единицы распознавания. Это решение существенно влияет как на выбор описательных признаков, так и архитектуру системы в целом. В качестве единиц распознавания могут быть использованы фонологические единицы: аллофоны, фонемы, дифоны, слоги, слова или некоторые их сочетания (рис. 1).

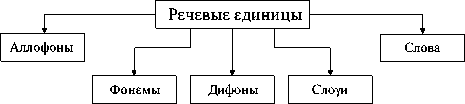
Рис. 1. Речевые единицы

В настоящее время создание систем распознавания речи ориентировано либо на использование в качестве эталонов целых слов, что удобно для применения в системах с ограниченным словарем, например для ввода небольшого набора команд, либо на использование метода, основанного на выделении фонем из потока речи, т. е. фонемно-ориентированного метода. Его преимущество состоит в том, что при увеличении словаря качество распознавания не снижается.

Сравнив методы распознавания целых слов и фонем, можно сделать следующий вывод: при небольшом количестве слов, используемых диктором, более высокая надежность и скорость работы наблюдается при распознавания целых слов, но при увеличении словаря характеристики резко падают. И размер словаря системы распознавания уже в сотню слов делает актуальным переход на уровень более низкий, чем распознавание слов в целом. Преимущество использования фонемно-ориентированного метода связано с тем, что набор фонем для любого языка представляет собой наименьшее число отличительных фонологических классов, которые должны быть распознаны. Система фонем русского языка насчитывает 44 единицы [1].

Одной из основных проблем, возникающих в процессе создания систем распознавания речи, является выбор признаков, позволяющих наиболее полно описать сигнал речевой единицы, а также метода их вычисления. Речевой сигнал является примером нестационарного процесса, в котором информативным является сам факт изменения его частотно-временных характеристик (рис. 2).

Необходимо определить такие параметры речевого сигнала, которые бы полностью описывали его, т. е. позволяли бы отличить один звук речи от другого, но были бы в какой-то мере инвариантны относительно вариаций речи.

Примером использования кепстральных характеристик при построении моделей фонем является модель Орегонского института науки и технологий. Модель фонемы в этом случае описывается как

Ф :К„.\К„Е,.\Е-, (1)

где К₁₂ -12 мел-частотных кепстральных коэффициентов; АК₁₂ -12 характеристик дельты МЕСС; Е - энергетическая характеристика; АЕ - дельта-характеристика энергии.

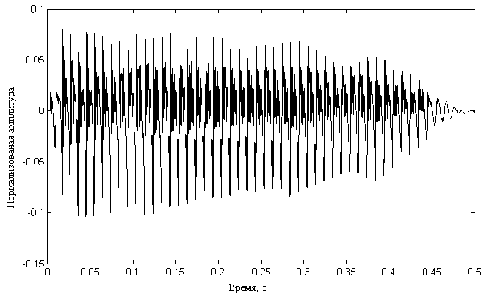
Рис. 2. Отображение речевого сигнала во временной области

Таким образом, для вычисления признаков речевого сигнала фонемы используется 12 мел-частотных кепстральных коэффициентов, 12 характеристик дельты МЕСС, которые указывают степень спектрального отклонения, 1 энергетическая характеристика и 1 дельта-характеристику энергии, в общей сложности 26 характеристик на окно. Также используется кепстральное вычитание мел-частотных кепстральных коэффициентов, предназначенное для удаления некоторых эффектов шума.

Чтобы получить информацию об акустическом окружении, берется контекстное окно характеристик, т. е. анализируются окна, находящиеся на 60, 30 мс до рассматриваемого окна и на расстоянии в 30, 60 мс после него, с учетом динамической природы речи, благодаря которой идентификация фонемы часто зависит не только от спектральных особенностей в некоторый момент времени, но также и от того, как эти особенности изменяются в течение долгого промежутка времени. Характеристики контекстного окна посылаются в нейронную сеть для классификации по 26 характеристик на каждое окно, всего для 5 окон -130 характеристик. На выходе нейронной сети будет получена классификация каждого входного окна, взвешенная в терминах вероятностей категорий на основе фонемы. Посылая контекстные окна для всех окон речи к нейронной сети, можно формировать матрицу из вероятностей категорий на основе фонемы.

Для нахождения лучшего пути через матрицу вероятностей для каждой строки используется поиск Витерби. Вывод распознавания программы - это строка слова, которая соответствует лучшему пути. Подобная модель фонемы была предложена в системе автоматического распознавания русской речи «Sirius» Санкт-Петербургского института информатики и автоматиации РАН [2], в которой использовались мел-частотные кепстральные коэффициенты с их первой и второй производными, а для распознавания применялись методы скрытого марковского моделирования.

Распространенными методами вычисления признаков речевого сигнала являются методы, основанные на преобразовании Фурье, в частности гомоморфный анализ, позволяющий определить частоту основного тона путем вычисления кепстра речевого сигнала и измерить формантные частоты с помощью кепстрально-сглажен- ного логарифма спектра. В данном методе анализ сводится к измерению параметров цифровой модели рече-образования, где сигнал рассматривается как свертка компонентов [3]:

x(n) = u(n) • s(n),                  (2)

где s(n) - сигнал возбуждения; u(n) - импульсная характеристика голосового тракта. При этом сигналом возбуждения s(n) считается свертка последовательности импульсов основного тона_p(n) и импульсов возбуждения e(n): s(n) =р(н) • е(n).                    (3)

Операция свертки (2) легко приводится к суммированию, если применить дискретное преобразование Фурье (ДПФ), что дает произведение, и прологарифмировать результат [3]. Данное свойство используется в алгоритме, позволяющем оценить параметры каждой составляющей x(n) в отдельности (рис. 3).

Дискретное преобразование Фурье от x(n) дает сигнал, равный произведению ДПФ от и(п) и s(n):

N - ¹         - i 2 П kn

X ⁽ k ) = £ x ⁽ n ) e N ,              (4)

k = 0

X(k) = U(k) S(k).                (5)

В следующем блоке определяется логарифм модуля полученной последовательности, причем сигнал в точке С равен сумме логарифмов модулей ДПФ от s(n) и и(п): log(Rk)l) - log(|U(k)|) + log(|5(k)|).      (6)

Поскольку обратное ДПФ линейно, сигнал в точке D, называемый кепстром сигнала в точке И, равен сумме кепстров функции возбуждения и импульсной характеристики голосового тракта и позволяет разделить эффекты возбуждения и характеристики голосового тракта [3] (рис. 4).

Кепстр, полученный описанным выше способом, исследуется с целью отыскания пика в области возможных значений периода основного тона (4.. .40 мс), соответственно вычисляется и частота основного тона:

foe.= ~ ,                      С7)

ULH

T0

где Т₀ - период основного тона.

Часть кепстра в области времени, меньше чем период основного тона, содержит главную информацию о речевом тракте. Применяя к данному компоненту ДПФ, получают кепстрально-сглаженный логарифм спектра (рис. 5). Этот спектр отражает резонансную структуру речевого сигнала, т. е. пики в спектре соответствуют формантным частотам. Оцениваются первые три формантные частоты, так как именно им принадлежит основная роль при формировании звуков.

Но методы, основанные на преобразовании Фурье, в своем традиционном виде не приспособлены для анализа нестационарных сигналов. Их использование требует соблюдения условия стационарности сигнала в пределах некоторого промежутка времени, что ограничивает точность анализа локальных изменений сигнала. Например, дискретное преобразование Фурье (3) не позволяет отличить сигналы, состоящие из двух синусоид с разными частотами, один из которых равен сумме синусоид (8), а второй представляет собой последовательно следующие друг за другом синусоиды (9) [4]:

x(n) = sin(n) + sin(3n),               (8)

x ( n ) =

sin ( n ) , n <  0

sin ( 3 n ) , n >  0 ,

Весовая функция

Весовая функция

Кепстра

Рис. 3. Гомоморфная обработка речи

В обоих случаях их спектр будет представлять собой два пика на фиксированных частотах (рис. 6, 7).

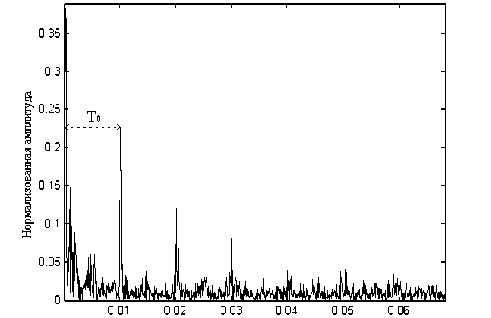
Время, с

Рис. 4. Кепстр вокализованного сигнала

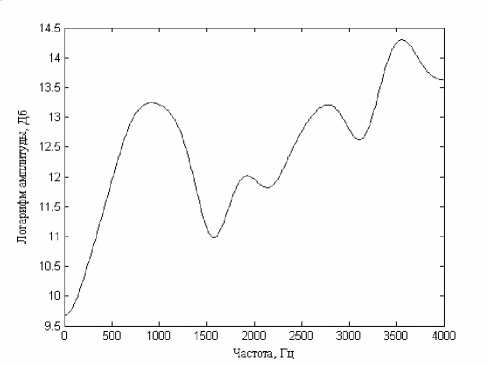
Рис. 5. Кепстрально-сглаженный логарифм спектра

Для построения модели фонемы автором предлагается использовать вейвлет-преобразование, в частности многомасштабный (кратномасштабный) вейвлет-анализ, который состоит в представлении сигнала последовательностью образов с разной степенью детализации, что позволяет выявлять локальные особенности сигнала и классифицировать их по интенсивности. В этом случае модель фонемы можно представить в виде набора средних значений энергии вейвлет-коэффициентов для каждого уровня детализации:

ф = {^а^Д (10) где W- значения средней энергии вейвлет-коэффициентов для 10 уровней детализации; АЛ/. значения среднего квадратического отклонения вейвлет-коэффициентов для 10 уровней детализации;^- число уровней детализации вейвлет-преобразования.

Средняя энергия вейвлет-коэффициентов для определенного уровня детализации / определяется следующим образом:

• 1    Lj - 1

^wrT Y d ь k ^, OD L j k = 0

где d _k- детализирующие коэффициенты; k - номер вейвлет-коэффициента;£. - количество вейвлет-коэффициентов в анализируемом окне на уровнеД

Многомасштабный вейвлет-анализ основывается на разложении сигнала по функциям, образующим орто-нормированный базис [4]. Любую функцию можно разложить на некотором заданном уровне разрешения (мас-штабе)у/ в ряд вида

• 2    M - 1 j max 2 M - 1

f ⁽ x ) = Y jk Ф у „, k ⁺ Y Y d j,k v j . k , ⁽¹²⁾ k = 0 n n j = jn k = 0

где Ф j n , _k и ш j , _k - масштабированные и смещенные версии скейлинг-функции (масштабной функции) ф и материнского вейвлета г; s j , _k - коэффициенты аппроксимации; d j , _k -детализирующиекоэффициенты.

Таким образом, метод вейвлет-анализа сигналов является наиболее предпочтительным для использования, так как данный метод не содержит сложных последовательностей действий, а признаки, получаемые в результате, характеризуют сигнал и во временной плоскости, и в частотной, что дает хорошие результаты для классификации (рис. 8,9).

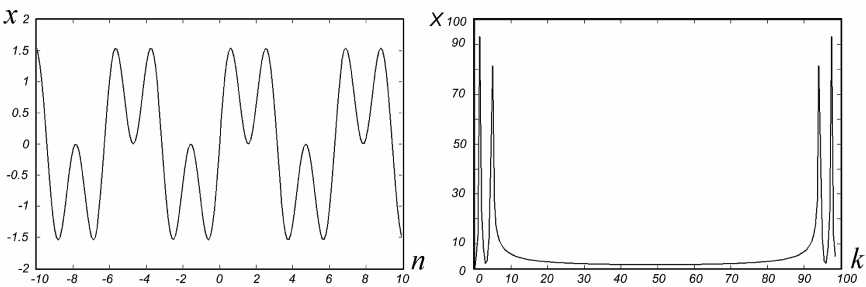
Рис. 6. График сигнала, описываемого функцией (8), и его фурье-спектр

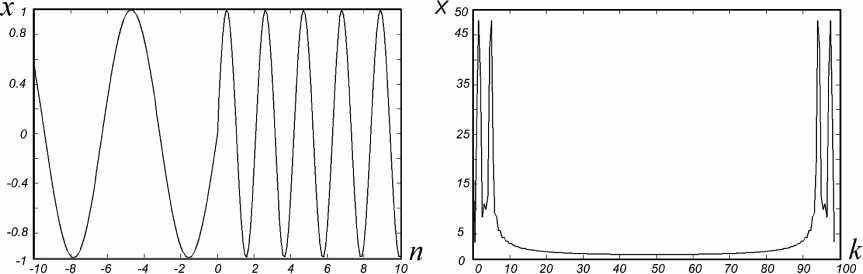
Рис. 7. График сигнала, описываемого функцией (9), и его фурье-спектр

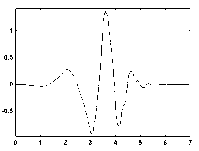
а

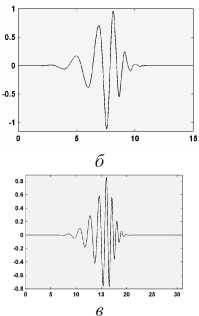
Рис. 8. Вейвлет-базисы: а - Добеши 4;

б - Добеши 8; в- Добеши 16

Проведенные экспериментальные исследования по выбору вейвлет-базиса показали, что наилучшие результаты достигаются при использовании базиса Добеши 8. Поскольку базис Добеши является ортонормированным, то это дает возможность использовать быстрый алгоритм вычисления вейвлет-коэффициентов на каждом частотном уровне по найденным коэффициентам на уровне с более высокой частотой.

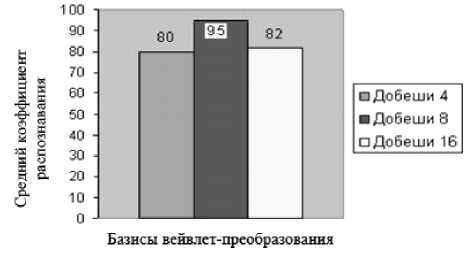
Рис. 9. Сравнительный анализ качества распознавания слов для разных типов вейвлетов

При использовании вейвлет-коэффициентов в качестве признаков, описывающих речевой сигнал, необходимо определить число уровней детализации, соответствующих размеру анализируемого частотного диапазона. Частотный диапазон речи равен примерно 20...20 000 Гц [1]. Вейвлет Добеши 8 имеет центральную частоту, равную 0,666 7 Гц. При частоте дискретизации 22 050 отсчетов в секунду получаем центральную частоту вейвлета, используемого для первого уровня разложения [4]:

Fr₁=Fr-Fd, (13)

Fr=0,666 7 22 050= 14 701.

С каждым следующим уровнем разложения частота вейвлета будет уменьшаться в два раза. Центральная частота вейвлета на десятом уровне разложения будет равна 28,7 Гц. Таким образом, вейвлет-коэффициенты для десяти уровней разложения отражают характеристики сигнала в указанном частотном диапазоне речи (рис. 10).

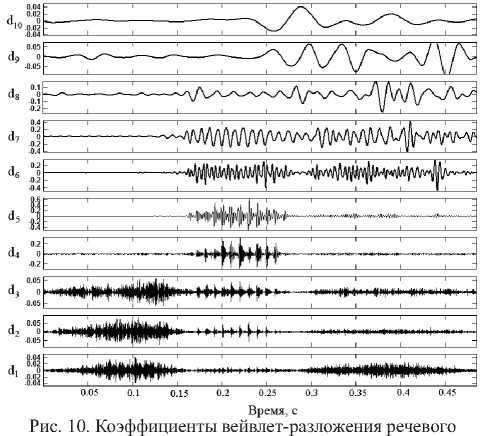
сигнала на 10 уровней детализации

В ходе проведения эксперементов определялась длина фиксированного интервала во временной области, на котором рассчитываются признаки речевого сигнала. Данный интервал должен быть меньше времени звучания фонемы. В русском языке длительности фонем изменяются в пределах 50.. .250 мс [1]. Значение длины сегмента должно позволять вычислять признаки речевого сигнала. Нижняя граница анализируемого частотного диапазона равна 28,7 Гц и в выделенный сегмент должен укладываться, по крайней мере, один период данной частотной составляющей, который равен 36 мс. Исходя из времени звучания фонемы в русском языке и анализируемого частотного диапазона, длина сегмента будет равна 36 мс.

Для оценки эффективности предложенного метода разработана вероятностно-сетевая модель системы преобразования речи в текст на основе нейронной сети с программной реализацией в срезе MatLAB [6]. Система дает возможность пользователю сформировать базу данных фонем, провести обучение нейронной сети с заданными параметрами на сформированной обучающей выборке и выполнить преобразование в текст представленного речевого сигнала. Для оценки качества работы системы преобразования речи в текст создана база данных фонем русского языка, включающая образцы речевых сигналов фонем дикторов различного пола и возраста и были проведены эксперименты по распознаванию фонем и слов. После обучения нейросети на сформированной базе признаков фонем-эталонов диктором, проводившим обучение, произносились отдельные фонемы и слова. По результатам экспериментов определялся коэффициент распознавания речевых единиц фонем (см. таблицу).

Таким образом эксперименты показали достаточно высокий коэффициент распознавания фонем, что определяет эффективность применения вейвлет-преобразова-ния для построения моделей фонем русского языка.