Использование возможностей стандартного прикладного программного обеспечения при решении инженерной задачи

Как известно, к стандартному прикладному программному обеспечению относится табличный процессор Microsoft Excel.

Ранее было описано, что расширенные возможности табличного процессора могут быть эффективно использованы при преподавании магистрантам дисциплин “Информационные технологии в теплоэнергетике” и “Информационные технологии в науке и образовании” в Карагандинском техническом университете [1].

Для изучения возможностей встроенного языка программирования VBA магистрантам была предложена стандартная для инженера задача:

В резервуаре правильной формы появляется отверстие (повреждение) через которое начинает вытекать вода . Площадь основания S0 , площадь отверстия S.Начальный уровень жидкости H0

Требовалось создать программу, которая позволила:

• -    осуществлять расчет изменения уровня воды в резервуаре в течении (то есть ее расход);

• -    иметь возможность изменения детализации (изменения шага) в заданном временном диапазоне.

Выбор в качестве инструментальногостредства табличного процессора было связано с теми преимуществами ,которые были ранее описаны:

• -    использование визуализации поля клеток;

• -    наличие встроенного языка программирования VBA;

• -    использование возможностей Recorder (записи действий пользователя) в виде программного кода [2].

Навыки по использованию Recorder были особенно актуальны и востребованы для инженеров-непрограммистов.

Стандартное решение задачи не представляло сложностей.

С помощью уравнения Бернулли и уравнения непрерывности получена формула для осуществления численного расчета изменения уровня жидкости в резервуаре:

Ah_z =^ 56= S At Jv-⁵

где Δh i – изменение уровня воды при i-м шаге за время Δt;

h i – значение уровня жидности;

Δt – величина выбранного временного промежутка;

• S 0 – площадь основания резервуара;

S – площадь пробоины.

С использованием разработанного программного средства был осуществлен численный расчет и визуализация (построение графиков).

На рисунке 1 представлен пример реализации заданных входных параметров.

Входные параметры соответствуют значениям:

Ho=5 м; Δt=60c (или 1 мин); S 0 = 10 м²; S=0,0077 м²

Динамика изменения уровня жидкости в зависимости от площади пробоины

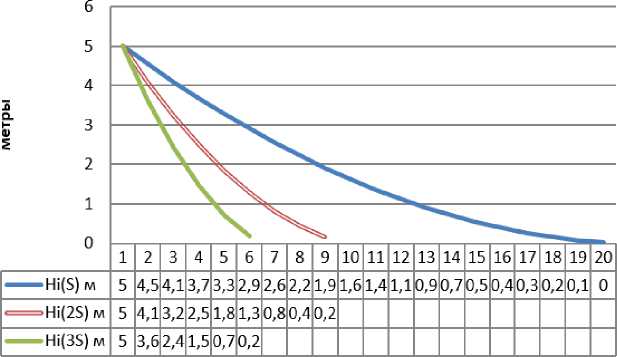
Рис. 1. Пример зависимости высоты уровня жидкости от площади пробоины

Разработанной программой предусмотрена возможность отслеживания динамики изменения уровня жидкости при значениях величины пробоины S:

• -    в 2 раза больше (2S) и

• -    в 3 раза больше (3S). Напомним, что S-оценка величины заданной пробоины. Очевидно ,что проверить эту оценку с использованием разработанной программы проблематично.

С этой точки зрения возникла идея расширения возможностей програм-мы.Подобные расширения программной реализации позволяют:

• -    оценивать размер самого повреждения по вытекшему количеству воды ;

• -    оценивать степень развития аварийности – то есть возможного степени роста размера повреждения

Расширенный функционал основан на решении обратной задачи – осуществление оценки величины пробоины S по количеству вылитой жидкости. Подобная постановка является более актуальной и близкой к производственной реализации .

Рассмотрим расширение программной реализации более детально.

Возьмем те же параметры Ho=5 м;

Δt=60c (или 1 мин) ;S0= 10 м2

Для приближения к реальности величину пробоины примем S=0,0007 м2 . С этой точки зрения изменение уровня воды выглядит так ,как показано на рисунке 2.

НП(м)

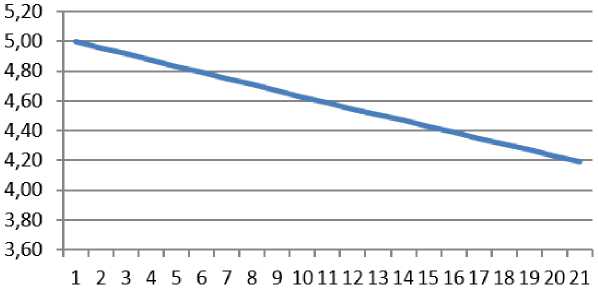
Рис. 2. Пример зависимости высоты уровня жидкости от площади пробоины

Hfl(M)

Предположив в качестве грубого приближения величину пробоины S=0,0003 м2 можно получить значение изменения уровня жидкости в предположении изменения величины пробоины при ее изменении.

В Таблице 1 значения Hf1 являются фактическими данными , а значения Hi(S) расчетными для величины пробоины S=0,0003 м2 ,значения Hi(2S) для величины пробоины 2S = 0,0006 м2 ,значения Hi (3S) для величины пробоины 0,0009 м2.

Таблица 1. Сопоставительная таблица экспериментальных и расчетных данных

S(м 2)	D (см)	t (мин)	Hf1 (м)	Hi(S) м	Hi(2S) м	Hi(3S) м
0,0003	1	0	5,00	5,00	5,00	5,00
		1	4,96	4,98	4,96	4,95
		2	4,92	4,96	4,93	4,89
		3	4,87	4,95	4,89	4,84
		4	4,83	4,93	4,86	4,79
		5	4,79	4,91	4,82	4,73
		6	4,75	4,89	4,79	4,68
		7	4,71	4,87	4,75	4,63
		8	4,67	4,86	4,72	4,58
		9	4,63	4,84	4,68	4,52
		10	4,59	4,82	4,65	4,47
		11	4,55	4,80	4,61	4,42
		12	4,51	4,79	4,58	4,37
		13	4,47	4,77	4,54	4,32
		14	4,43	4,75	4,51	4,27
		15	4,39	4,73	4,47	4,22
		16	4,35	4,72	4,44	4,17
		17	4,31	4,70	4,41	4,12
		18	4,27	4,68	4,37	4,07
		19	4,23	4,66	4,34	4,02
		20	4,19	4,65	4,30	3,98

В соответствии с таблицей 1 построен график зависимостей изменения уровня жидкости в зависимости от времени (рис. 3).

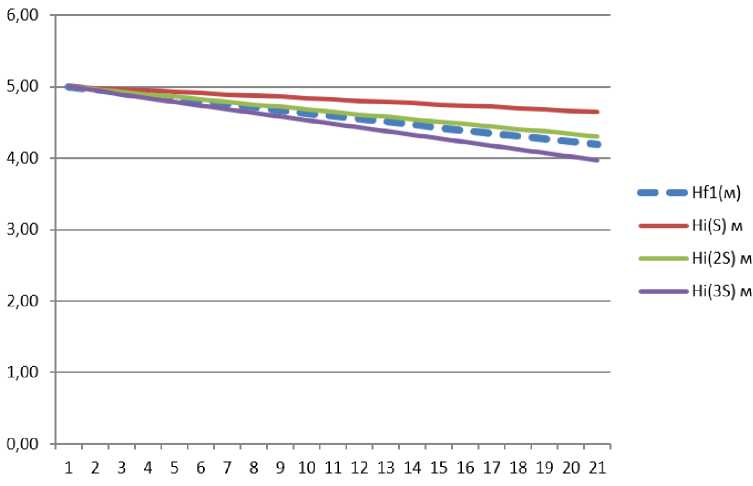
Рис. 3. Сопоставление фактических и расчетных данных в выбранный промежуток времени

Из графика (рис. 3) видно, что размер

В заключении следует отметить, что повреждения находится между значениями Hi(2S) и Hi(3S), то есть между 0,0006 м2 и 0,0009 м2, причем немного больше 0,0006 м2.

Таким образом , расчетное значение повреждения составляет 0,0007 м2 , что очень близко к фактической оценке.

расширение постановки задачи позволило усилить возможности производственного использования рассматриваемой стандартной учебно-методической задачи.

Разработанное программное средство успешно используется в производственных процессах Энергообъединения АО «Астана-Энергия».