Использования Java для проверки компетенций по геометрическому моделированию
Автор: Макаров Евгений Маратович
Журнал: Образовательные технологии и общество @journal-ifets
Статья в выпуске: 1 т.21, 2018 года.
Бесплатный доступ
Описывается способ использования языка Java в курсе «Компьютерная геометрия и геометрическое моделирование» для проверки компетенции ОПК-4: «Способность находить, анализировать, реализовывать программно и использовать на практике математические алгоритмы, в том числе с применением современных вычислительных систем». Приводятся примеры задач для оценки уровня этой компетенции, и обсуждается, как программирование на Java может использоваться для проверки решений этих задач.
Геометрическое моделирование, электронное обучение, аффинное отображение
Короткий адрес: https://sciup.org/140224561
IDR: 140224561
Текст научной статьи Использования Java для проверки компетенций по геометрическому моделированию
В 2011 году в рамках реализации Болонского процесса в России были введены новые федеральные государственные стандарты (ФГОС), важнейшей частью которых является компетентностный подход. Он предусматривает перенос фокуса образования с преподавания и проверки знаний на выработку взаимосвязанных характеристик: знаний, умений, навыков, способностей и личностных качеств [1–4]. Таким образом, результатом обучения должна явиться способность свободно ориентироваться в предметной области, решать профессиональные задачи на основании опыта и при необходимости находить дополнительную информацию.
Компетенции для каждого направления обучения зафиксированы в ФГОС. Для каждой дисциплины формулировки компетенций, вырабатываемых этой дисциплиной, записываются в рабочую учебную программу (РПД). Вместе с ними записывается наполнение компетенции в контексте конкретной дисциплины в виде показателей (индикаторов), а также критерии оценки сформированности компетенции. К РПД прилагается фонд оценочных средств, состоящий из заданий, таких как контрольные работы, тесты, собеседование и проекты, которые служат для проверки всех аспектов формирования компетенции.
В стандарте по направлению бакалавриата 02.03.01 «Математика и компьютерные науки»1 имеется компетенция ОПК-4: «Способность находить, анализировать, реализовывать программно и использовать на практике математические алгоритмы, в том числе с применением современных вычислительных систем». В данной статье описывается предложения по обучению этой компетенции в дисциплине «Компьютерная геометрия и геометрическое моделирование», преподаваемой на третьем курсе в Институте информационных технологий, математики и механики Нижегородского государственного университета им. Н.И. Лобачевского. В рамках этой дисциплины рассматриваются как теоретические вопросы компьютерного моделирования, такие как аффинные и проективные отображения, кривые Безье, и сплайны, так и использование этих понятий при программировании на языке Java. Мы рассмотрим всего лишь одну задачу, умение решать которую можно отнести к ОПК-4: использование аффинных отображений для построения изображений на экране компьютера. В рамках этой задачи к компетенции ОПК-4 можно отнести следующие показатели:
знать определения и основные свойства линейных, аффинных и проективных отображений, формулы наиболее важных отображений;
уметь находить матрицы линейных и аффинных отображений;
уметь переводить мировые координаты двумерной фигуры в экранные;
владеть навыками построения изображения двумерных и трёхмерных фигур на экране компьютера.
В статье показано, что для овладения этой компетенцией недостаточно знать факты об аффинных отображениях: нужно также уметь использовать их на практике и обладать навыками выбора способа решения практических задач.
Поскольку курс читается на направлении «Математика и компьютерные науки», он в большей степени, чем, скажем, курсы по компьютерной графике на более прикладных направлениях, ориентирован на изучение математических понятий и теорем, лежащих в основе способов изображения объектов. Сделана попытка не просто решить задачу, а связать её с материалом из более ранних курсов по аналитической геометрии и линейной алгебре и строго доказать корректность используемых методов изображения. С другой стороны, знание теоретических основ должно не остаться абстрактным, а послужить обоснованием тех практических соображений, которые используются программистами при использовании графической библиотеки Java.
В следующем разделе содержится напоминание понятий, связанных с аффинными преобразованиями и вводятся необходимые обозначения. Затем мы кратко перечисляем средства векторной графики, имеющиеся в языке Java, и описываем, как заготовки программ, выданные студентам, могут использоваться для проверки решения задач построения изображений. Часть материала ниже основана на учебно-методическом пособии автора [5].
Аффинные преобразования
Будем обозначать реперы на плоскости фигурными буквами, такими как У, а координаты точки р в репере У — через . Координаты обычно рассматриваются в виде вектора-столбца.
Как известно, - С'[^ ]*^, где через ^т* обозначена матрица перехода из базиса, входящего в репер У, в базис репера У’ . Если перейти к однородным координатам и матрицам размера на единицу больше, то это равенство [О'И
/ \ 0 1
можно записать как , где есть блочная матрица называемая матрицей перехода из у в У’ .
Если J — аффинное преобразование, то КЛ называется матрицей J в репере у и обозначается Ш^7. В более общем случае можно рассмотреть матрицу преобразования по отношению к двум реперам у и у! ; тогда матрицей / называется
.
Таким образом одна и та же матрица может рассматриваться как матрицей преобразования, так и матрицей перехода. В первом случае [/2 ° /1JT7 = ([/2]-^) ([/1]-^) : матрицы последовательных преобразований записываются справа налево, причём все преобразования рассматриваются в одном репере. Во втором случае ^3 7-2 : матрицы последовательных переходов записываются слева направо, но при этом матрица каждого следующего преобразования берётся в предыдущем репере. Для развития навыка построения изображения на экране компьютера имеет большое значение умение выбрать наиболее удобный взгляд на матрицу в конкретной задаче и умение строго объяснить, как происходит преобразование координат из одной системы в другую.
Введём обозначения для стандартных преобразований. Если Т = (O,ei,e2) — ортонормированный репер, то поворот вокруг О на угол а , масштабирование вдоль ci и 6-2 с коэффициентами Аи М- , соответственно, а также параллельный перенос на вектор с координатами (ж, у) являются аффинными отображениями со следующими матрицами в у .
( cos а sin а
О
— sin а cos а О
0\ /А 0 0\ /10х\
0 I , 5(А,д) = I 0 /2 0 I , Т(ж,у) = I 0 1 у I(1)
1/ \0 0 1/ \0 01/
Если А или Мв s^A отрицательны, то кроме масштабирования преобразование включает в себя симметрию относительно соответствующей оси координат.
Все задачи, которые рассматриваются в данной статье и используются для развития компетенции ОПК-4, имеют целью перевод координат фигуры в одной системе координат в координаты образа этой фигуры в, возможно, другой системе координат. В качестве важного примера рассмотрим перевод фигуры из мировой системы координат в экранную (window to viewport transformation) [6–8]. Как обычно, начало экранной системы координат расположено в левом верхнем углу экрана или окна, ось X направлена вправо, а ось У — вниз.
Пример 1.
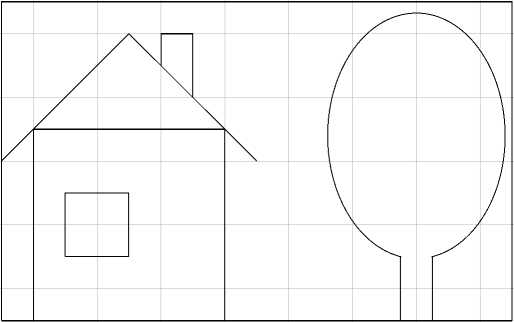
В мировой системе координат, где единицами измерения служат метры, задана фигура, показанная на рис. 1. Требуется изобразить её в окне, имеющем высоту h пикселей, границу шириной Р пикселей и разрешение г пикселей на сантиметр. Изображение должно быть выполнено в масштабе m метров в одном сантиметре и располагаться в левом нижнем углу окна, то есть левый нижний угол фигуры с мировыми координатами (xw,yw) = (3,1) должен иметь экранные координаты
= (h -p.p) . Описанное расположение изображено на рис. 2.
8 G 4
2 4 G 8 10 12 14 16 18 20
Рис. 1. Фигура в мировых координатах
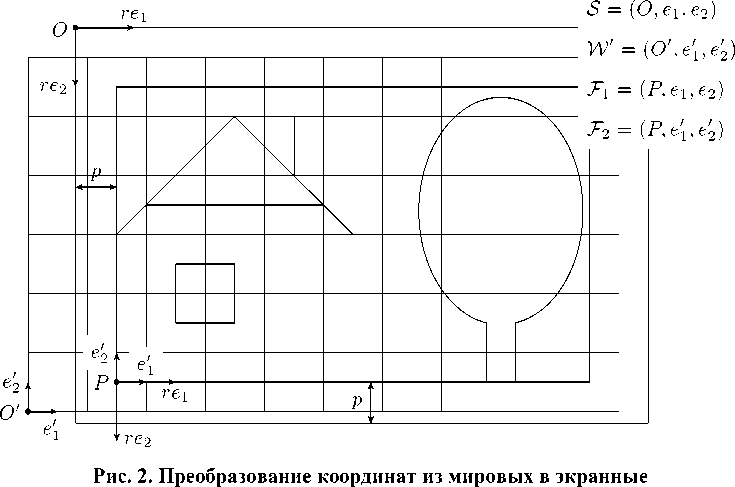
Пусть w и S = (O, ei,e2)— реперы, задающие мировую и экранную системы координат, соответственно. Тогда длины векторов ?’ei и re2 равны 1 см. Далее, пусть F— точка с экранными координатами ^s^s^ . Рассмотрим репер W' = (O', 61,62), где e'l = le'2| = l/m см и [P]4V' = (жи,,ую). Тогда аффинное преобразование /, переводящее wв wz, переводит исходную фигуру в требуемое изображение в окне, поэтому задача сводится к отысканию Vf^w^ = Dw- .
Рассмотрим два дополнительных репера = (F, ei,e2) и Г-1 = (Fe^e?,); тогда W'. Эти матрицы переходов удобно рассматривать как матрицы преобразований: и uw есть матрицы параллельных переносов на векторы ^s^s) и (-хш, -yw), соответственно, поскольку координаты векторов переноса определяются в реперах s и . Преобразование, переводящее 3"i в ^2 , есть масштабирование с центром в точке Р и коэффициентами т и —т(т . Общая матрица перехода есть
Dw- = T($s,ys)S(r/m,-r/m)T(-;rw,-yw). ( 2 )
Векторная графика в Java
В курсе «Компьютерная геометрия и геометрическое моделирование» язык программирования Java используется как для решения и оценки задач, так и для написания программных проектов. Язык Java является хорошим выбором для работы с графикой по следующим причинам:
он очень популярен;
он обладает собственной библиотека Swing для создания графического интерфейса, которая одинаково работает в разных операционных системах;
Java часто используется во вводных курсах программирования, а если в таких курсах используется C++, то с него достаточно просто перейти на Java;
компилятор, библиотеки и средства разработки на Java являются бесплатными.
Согласно нашему опыту, для того, чтобы дать студентам, изучавшим C++ на младших курсах, достаточно информации для написания программ с графическим интерфейсом на Java, достаточно трёх лекций и трёх практических занятий.
Поскольку студенты все равно должны выучить Java, чтобы писать проекты (используя заготовки преподавателя), написание маленьких программ можно использовать для решения теоретических задач.
К сожалению, даже самые простые программы на Java, использующие графику, содержат немало конструкций, объяснение которых требует время. Так, на рис. 3 показана минимальная программа для рисования. Она может быть предоставлена преподавателем ещё до объяснения тонкостей программирования графического интерфейса, и студентам нужно только добавить код для создания фигур и аффинных отображений, а также собственно для рисования.
Аффинные отображения в Java представляются объектами класса AffineTransform . На рис. 4 приведены основные методы этого класса, меняющие отображение. Чтобы получить объект AffineTransform , содержащий поворот, масштабирование или перенос, можно создать тождественное отображение с помощью конструктора, а затем применить к нему нужный метод.
setOpaque(true);
setPreferredSize(new Dimension(500, 500));
}
@Override public void paintComponent(Graphics g) { super.paintComponent(g);
Graphics2D g2 = (Graphics2D) g;
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING,
RenderingHints.VALUE_ANTIALIAS_ON);
// Код для рисования записывается сюда
} private static void createAndShowGUI() {
JFrame frame = new Jframe("");
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setVisible(true);
} public static void main(String[] args) {
SwingUtilities.invokeLater(Drawing::createAndShowGUI);
}
}
Рис 3. Минимальна программа для рисования
Методы AffineTransform
Действие
A ;= Е (единичная матрица)
А := Ат
А := ААг
А — АЩО)
А := AS^x, у)
А := АТ^х, у)
A = new AffineTransform()
A = new AffineTransform(A1)
A.concatenate(A1)
A.rotate(theta)
A.scale(x,y)
A.translate(x,y)
Рис. 4. Методы AffineTransform . Переменная A имеет тип AffineTransform
Для представления фигур в Java имеются классы Line2D (отрезок), Rectangle2D (прямоугольник), Ellipse2D (эллипс), Arc2D (дуга эллипса), а также QuadCurve и CubicCurve (кривые Безье второй и третьей степени, соответственно). К этим названиям добавляется .Double для обозначения классов с координатами, представленными числами типа double. Кроме того, имеется класс Path2D.Double для представления составных фигур. В нем есть методы moveTo(x, y) для перемещения текущей точки в (т, у), lineTo(x, y) для соединения текущей точки с (•г1, У) отрезком, а также метод append() для добавления целой фигуры. Аффинное отображение А можно применить к фигуре s вызовом A.createTransformedShape(s).
Использование Java для проверки решения задач про аффинные отображения
Пусть S — репер, задающий экранную систему координат. Невырожденную матрицу А можно рассматривать как матрицу перехода Dw от S к некоторому реперу W , задающему мировую систему координат. Тогда A.concatenate(A1) вводит новую мировую систему координат с репером W , где Dw- — ^i .
Таким образом в окне программы легко задать систему координат используемую в той или иной задаче. Студент может решить задачу по нахождению отображения на бумаге и затем проверить правильность решения, скомпилировав и запустив программу.
Пример 2.
В декартовой системе координат дана прямая I с уравнением у = X + 1 . Найти матрицу Si симметрии относительно I в исходной системе координат (рис. 5).
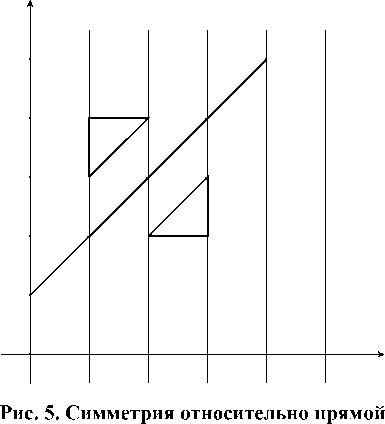
Пусть у — репер, задающий исходную систему координат, и пусть У получается из у сдвигом на единицу вверх и последующим поворотом на 45°. Матрица искомой симметрии в У' есть S(l,-1) (см. (1)), поэтому согласно хорошо известному факту о матрице отображения в другом репере Si = D 1S(1, — 1)D , где D . Матрицу D можно представить с помощью композиции переходов: D = R(— тг/4)Т(0, —1). В итоге
St = T(0,1)Д(тг/4)5(1, -1)Я(-тг/4)Т(0, -1). (3)
Преподаватель высылает студенту или выкладывает на сайт курса файл-оболочку на рис. 3, где в метод paintComponent() вставлен код на рис. 6. Преобразование cs соответствует мировой системе координат, где начало находится в левом нижнем углу окна (метод getHeight() возвращает высоту окна в пикселях), ось У направлена вверх, а единичный отрезок равен 50 пикселям. Программа рисует отрезок из (0,1) в (^ 5) , представляющий прямую, относительно которой нужно осуществить симметрию. Также рисуется треугольник с координатами (1, 3), (1,4) и (2? 4) в качестве примера фигуры. Отображение at , определение которого студенту нужно закончить, инициализировано тем же преобразованием cs .
AffineTransform cs = new AffineTransform();
cs.translate(0, getHeight());
AffineTransform at = new AffineTransform(cs);
Рис. 6. Заготовка программы в задаче про симметрию относительно прямой
Формула (3) и рисование образа фигуры при отображении записывается в Java в виде кода на рис. 7.
at.translate(0, 1);
at.translate(0, -1);
Рис. 7. Решение задачи про симметрию относительно прямой
В решении данной задачи можно сделать ряд ошибок, и важно не только избежать их, но и уметь объяснить каждый шаг. Так, матрица Т(О, -1)Я(-тг/4) с перепутанным порядком поворота и параллельного переноса есть матрица перехода из у' в репер с началом в Ы^Ф, 1 - V2/2) вместо у . Кроме того, поскольку матрица преобразования известна в У , но неизвестна в У , нужно рассматривать матрицу перехода из F в У , а не наоборот, несмотря на то, что У задаёт исходную систему координат. Для решения подобной задачи часто требуется несколько попыток.
В качестве решения задачи студент высылает код на рис. 7 или всю программу, а также краткое объяснение формулы (3).
Пример 3.
О О' е1
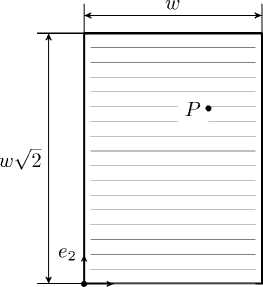
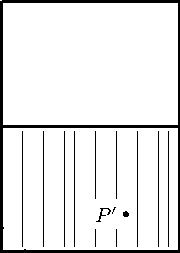
Рис. 8. Масштабирование листа формата А4
Отношение высоты к ширине листа бумаги любого формата серии A (например, A4) равно V2 и 1,414. Это позволяет в точности разместить две уменьшенные и повёрнутые на 90° копии страницы на одной странице, как показано на рис. 8. Пусть при таком преобразовании точка р переходит в р! , и пусть заданы реперы У = (О, ci, е2) и F = (O',ei,e2) с началами в левых нижних углах страниц. Найти матрицу, преобразующую [Р]-^7 в ^Р^Р , если размер исходной страницы есть w х h в единицах, задаваемых векторами ^1 и ^2 .
Пусть / есть искомое отображение; требуется найти матрицу Г#1 ij: у>\ _ qF’
. Записывая матрицы последовательных переходов слева направо, получаем, что искомая матрица есть
Т(0, /t/2)P(-7r/2)S'(l/V2,1/V2). (4)
Вместе с задачей студенту даётся заготовка на рис. 9. В ответ он высылает код на рис. 10, рисующий уменьшенную страницу, вместе с объяснением формулы (4). Эта формулу можно получить, рассматривая композицию отображений вместо последовательности переходов к новым реперам, но в любом случае требуется предъявить доказательство правильности полученной матрицы.
Приведём ещё несколько примеров аналогичных задач.
AffineTransform cs = new AffineTransform(); cs.translate(0, getHeight());
double w = 210;
double h = 297;
AffineTransform at = new AffineTransform(cs);
Рис. 9. Заготовка программы в задаче про поворот страницы at.translate(0, pageHeight/2);
Рис. 10. Решение задачи про поворот страницы
Пример 4.
Дан график функции sin x на отрезке [—тг/2, тг/2] . Найти аффинное преобразование, которое нужно к нему применить, чтобы этот график был нарисован в центре окна размером w х h пикселей, а единичный отрезок занимал 30 пикселей. Также найти преобразования, переводящие исходный график в изображения графиков следующих функций:
cos x на [О, тг];
arcsine на [— 1.1];
arccos x на [-1,1].
Пример 5.
Метод void drawString(String str, float x, float y) печатает строку str в точке с координатами (^’: У) . Точка находится непосредственно слева от строки на её базовой линии , как показано на рис. 11. Аффинное преобразование действует на печатаемые символы. Направление текста совпадает с направлением оси Ox мировой системы координат, а буквы направлены в ту сторону от базовой линии, которая противоположна оси Oy . Таким образом, при тождественном аффинном преобразовании буквы расположены обычным образом (а не перевёрнуты).
Требуется нарисовать окружность радиуса r и буквы слова «Окружность», равномерно распределенные вокруг неё. Вертикальная ось букв должна быть направлена к центру окружности, как показано на рис. 11. Расстояние от центра до базовой линии букв равно l,lr. Найти функцию, которая по номеру г возвращает матрицу преобразования, которое нужно применить перед вызовом drawString(c, 0, 0) , где c — i -я буква слова.

Рис. 11. К примеру 5
В качестве более крупного программного проекта по теме аффинных отображений студентам предлагается дописать заготовку программы, которая, аналогично примеру 1, помещает изображение в один из углов или в центр окна (рис. 12). Масштаб изображения в пикселях на сантиметр при этом может быть фиксированным, или изображение может занимать всю ширину или всю высоту окна. Режимы изображения задаются кнопками справа. Код, реализующий графический интерфейс предоставляется преподавателем, и студенты должны лишь написать код, возвращающий требуемое аффинное преобразование в зависимости от значений переменных, которые соответствуют кнопкам. Так, преобразование (2) получается с помощью следующего фрагмента.
AffineTransform at = new AffineTransform();
at.translate(xs, ys);
at.translate(-xw, -yw);
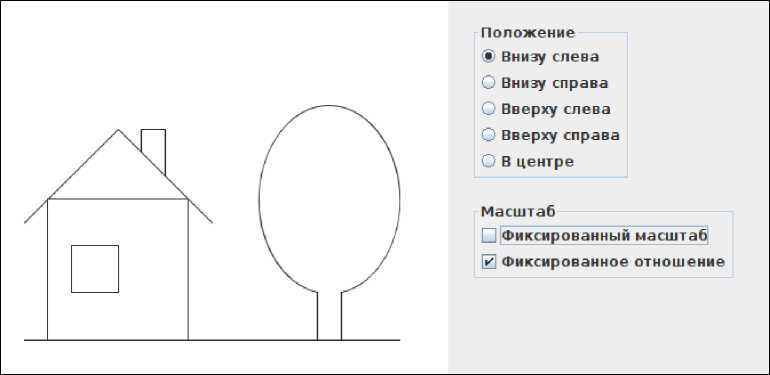
Рис. 12. Программный проект
Заключение
В статье рассматривается компетенция ОПК-4 «Способность находить, анализировать, реализовывать программно и использовать на практике математические алгоритмы, в том числе с применением современных вычислительных систем» для бакалавриата по направлению «Математика и компьютерные науки». Предложены возможные показатели и описаны оценочные средства для этой компетенции.
Аффинные отображения широко используются при построении изображения на экране компьютера. Теория этих отображений несложная и, как правило, рассматривается в курсах аналитической геометрии и линейной алгебры. Однако одного знания теории недостаточно для развития навыка построения изображения двумерных объектов. Первые попытки изобразить фигуру, заданную в абстрактных мировых координатах, часто приводят к тому, что изображение находится за пределами компьютерного окна или имеет неожиданную форму.
Представление матрицы искомого отображения в виде произведения стандартных матриц допускает разные обоснования, и выбор наиболее удобного из них требует опыта. Также легко допустить ошибку, подобную следующим:
перепутать направления перехода от одного репера к другому;
забыть, что при рассмотрении последовательности переходов матрица каждого из них записывается в предыдущем репере, а не в исходном, как при рассмотрении композиции отображений;
забыть, что в матрице поворота нужно изменить знак на побочной диагонали, если ось У направлена вниз.
Для развития навыка решения подобных задач незаменимым является возможность проверить правильность ответа на компьютере. Благодаря тому, что формулы, задающие аффинные отображения, записываются в Java почти так же легко, как на бумаге, есть возможность предоставить студентам заготовку программы, куда нужно только вписать операторы для создания требуемого отображения. Это позволяет студентам проверить себя и делает обучение более наглядным. Преподаватель оценивает фрагменты, присланные студентами (для этого можно запустить полученную программу), а также теоретические объяснения используемых формул. Таким образом, компетенцию ОПК-4 можно развивать дистанционно.
Использовать компьютер для проверки решения задач можно прямо во время собеседования во время промежуточной аттестации, внося изменения в заготовку программы и перекомпилируя её. Так, например, уровень владения навыками ОПК-4 может оценить по количеству попыток решения упражнения в примере 4.
В будущем мы планируем написать набор онлайн-тестов, которые бы исключили необходимость вносить изменения в код программы для получения изображения. Это сделает проверку ответа более удобной и позволит проводить дистанционное тестирование с ограниченным количество попыток решения.
Список литературы Использования Java для проверки компетенций по геометрическому моделированию
- Гергель В.П., Гугина Е.В., Кузенков О.А. Разработка образовательного стандарта Нижегородского госуниверситета по направлению «Фундаментальная информатика и информационные технологии»//Современные информационные технологии и ИТ-образование. -2010. -Т. 1, № 6. -С. 51-60.
- Ключевые ориентиры для разработки и реализации образовательных программ в предметной области «Информационно-коммуникационные технологии»/И.Ю. Петрова //Бильбао. -2013.
- Захарова И.В., Кузенков О.А. Опыт реализаций требований образовательных и профессиональных стандартов в области ИКТ в российском образовании//Современные информационные технологии и ИТ-образование. -2016. -Т. 12, № 3-1. -С. 17-31.
- Модернизация программ математических дисциплин ННГУ им. Н.И. Лобачевского в рамках проекта МЕТАМАТН/О.А. Кузенков //Нижегородское образование. -2016. -№ 1. -С. 4-10.
- Макаров Е.М. Элементы двумерной графики в Java. -Нижегородский государственный университет им. Н.И. Лобачевского, 2017. -URL: http://www.unn.ru/books/met_files/graphics-java.pdf (дата обращения: 21.12.2017).
- Никулин Е. А. Компьютерная геометрия и алгоритмы машинной графики. -СПб: БХВ-Петербург, 2003.
- Klawonn F. Introduction to Computer Graphics Using Java 2D and 3D. -2nd ed. -Springer-Verlag, 2012.
- Eck D. J. Introduction to Computer Graphics/Hobart and William Smith Colleges. -2016. -URL: http://math.hws.edu/graphicsbook (дата обращения: 21.12.2017).


