Исследование алгоритмов определения параметров многодипольной модели сердца

Согласно многодипольной модели сердце состоит из конечного числа диполей, фиксированных в определенных точках миокарда и сохраняющих ориентацию вектора момента (обычно по нормали к участку поверхности сердца), но изменяющих во время кардиоцикла свою величину. Каждый из этих диполей отражает суммарную электрическую активность данного участка сердца. Суммарное действие всех всех диполей модели сердца формирует электрокардиосигнал (ЭКС), регистрируемый на поверхности тела.

В свою очередь, решение обратной задачи электрокардиографии, состоящей в получении характеристик электрической активности сердца (ЭАС) по данным зарегистрированным на поверхности тела, представляет исключительную диагностическую ценность, наряду с классическими методами амплитудно-временного, частотно-временного и нейросетевого анализа ЭКС [1].

Существенную роль в определении электрической активности играют геометрические харак-

теристики модели сердца, так как геометрическое место точек – элементарных генераторов, направления нормалей в этих точках напрямую влияют на результаты моделирования. Классически геометрическая модель сердца рассматривается как шар или эллипсоид [2], однако могут использоваться и полигональные модели, отражающие анатомические особенности строения сердца [3].

В данной работе проводится исследование алгоритмов определения параметров многодипольной модели сердца при моделировании ЭАС. В качестве электрической модели сердца авторами многодипольная модель.

МОДЕЛИРОВАНИЕ ЭАС

Моделирование ЭАС заключается в решении обратной задачи электрокардиографии [2]. Способ определения ЭАС предложен авторами в работе [4], он предполагает, совместное решение обратной и прямой задачи электрокардиографии и включает в себя следующие этапы:

• 1.    Регистрация и предварительная обработка первичной медицинской информации.

• 2.    Решение обратной задачи электрокардиографии.

• 3.    Решение прямой задачи электрокардиографии.

• 4.    Визуализация повреждений миокарда.

На первом этапе регистрируются данные, полученные в результате стандартного электрокардиографического обследования, а также регистрируются антропометрические данные пациента.

На этапе решения обратной задачи электрокардиографии по значениям потенциалов в конкретных точках на поверхности тела пациента определяются характеристики электрической активности сердца (ЭАС), в течение одного кардиоцикла. В качестве модели ЭАС принята многодипольная модель, которая состоит из определенного числа диполей, закрепленных на поверхности миокарда в определенных точках. Это теоретически позволяет получать детальную информацию о функционировании каждого участка поверхности сердца. Ограничением здесь выступает только размер вектор входных данных (электрических параметров, зафиксированных на поверхности тела), а также математический аппарат, позволяющий корректно и эффективно решать плохо обусловленные задачи решения больших систем уравнений, имеющих высокий уровень линейной зависимости [5]. Тело человека в такой модели ЭАС предполагается однородным и изотропным, обладающим неким удельным сопротивлением. Характеристики многодипольной модели ЭАС - это значения дипольных моментов Di, вычисленные по потенциалам ц _j , зарегистрированным в точках стандартных отведений:

р Д cos а ....

%(t) = Т-Е---T^DXt), j = 1-N, (1)

4л ~ r^

где Ф j ( t ) — суммарный поверхностный потенциал в точке измерения j [В];

P - среднее удельное сопротивление тела [Ом . м];

a ji - угол между вектором дипольного момента D_i и прямой, соединяющей j-ю точку отведения с каждым диполем сердца;

r_ji – расстояние от диполей модели сердца до точек отведений [м];

D_i ( t ) –дипольный момент i -го диполя модели сердца ( i = 1... I ) [А . м];

I – количество диполей модели сердца;

N – количество отведений.

Для повышения устойчивости решения обратной задачи принимается допущение о неизменности расположения и ориентации составляющих диполей. Предполагается, что вектор дипольного момента каждой точки модели сердца на протяжении всего рассматриваемого периода времени ориентирован вдоль неподвижной прямой, совпадающей с направлением нормали к данной точке модели сердца. Направления составляющих диполей определяются заранее и при решении обратной задачи считаются известными.

Для определения электрических характеристик сердца необходимо решить обратную задачу для многодипольной модели. Для ее решения согласно выражению (1) необходимо знать расположение диполей сердца, точек отведений и по- тенциалов в точках отведений на торсе пациента. Расположение диполей сердца задается координатами точек в декартовой системе координат модели сердца.

АЛГОРИТМЫ

Авторами рассматриваются два алгоритма поиска характеристик многодипольной модели сердца D _1-12. Оба алгоритма включают в себя математический аппарат решения системы уравнений и различия их состоят только в используемом критерии, согласно которому среди множества решений определятся итоговое решение.

Первый алгоритм в качестве такого критерия использует минимум суммы квадратичных отклонений между измеренными и рассчитанными потенциалами, то есть минимизируется среднеквадратичная невязка следующего вида:

N                        ²

F = Ё (%Хt) -ФЛд_12)(t)) = Fmin , (2) j i

где фj (t) - измеренный потенциал в точке j отведения, фim Xt) — потенциал в точке j отведения, (D1-12)

рассчитанный с использованием многодипольной модели, состоящей из 12 диполей.

Во втором алгоритме используется критерий следующего вида:

Ф       (t)-ф7(t) = 0, j = 1...12,    (3)

^{J (} D 1 - 12)               ^J

В качестве метода решения системы уравнений в обоих случаях использовался один и тот же метод – это метод Левенберга-Марквардта, разница состояла лишь в особенностях подачи уравнений в функцию – вычислитель. Стоит оговориться, что критерий подобный (3) уже предлагался при решении обратной задачи электрокардиографии, однако тогда для решения уравнений использовался другой метод - метод Гаусса – Ньютона, а в качестве электрической модели использовался точечный диполь [6].

Согласно предлагаемому подходу определения ЭАС (см. рис. 1) решение прямой задачи электрокардиографии используется для верификации решения обратной задачи.

Для решения прямой задачи необходимо:

• -    выбрать альтернативную модель ЭАС;

• -    установить взаимосвязь полученных в ходе решения обратной задачи электрокардиографии характеристик ЭАС с параметрами альтернативной модели ЭАС;

• -    определить параметры альтернативной модели ЭАС;

• -    установить критерий проверки алгоритмов решения обратной задачи по полученным параметрам альтернативной модели и параметрам многодипольной модели ЭАС.

На данный момент существует ряд моделей ЭАС, которые используются в исследованиях электрического поля сердца. Эти модели позволяют определять состояние сердца через его электрические параметры относительно выбранного центра системы координат, предназначенной для решения обратной задачи (диагностики) [2].

Одной из наиболее известных моделей ЭАС в области диагностики является дипольная модель эквивалентного электрического генератора. Теория эквивалентного диполя является теоретическим обоснованием электрокардиографии. В процессе кардиоцикла дипольный момент D_m , называемый в медицинской литературе интегральным электрическим вектором сердца, меняется по величине и направлению. ЭКГ представляет собой не что иное, как проекцию вектора D_m на выделенное электрокардиографическое отведение.

Несмотря на ряд преимуществ (наглядность, удобство визуального отображения, простота структуры при достаточно высокой точности аппроксимации измеренного потенциала), данная модель электрического генератора сердца, по мнению авторов, не пригодна для решения обратной задачи электрокардиографии, т.к. отсутствует возможность раздельного определения электрических характеристик разных частей сердца. Однако, для решения прямой задачи электрокардиографии, данная модель является вполне приемлемой, так как позволяет установить взаимосвязь между параметрами многодипольной модели с параметрами дипольной модели ЭАС. Поэтому в качестве альтернативной модели авторами был выбран дипольный эквивалентный токовый источник.

Основным параметром дипольной модели ЭАС является дипольный момент сердца D_m , который представляет собой согласно принципу суперпозиции сумму дипольных моментов элементарных диполей:

I

^Dm. = Z ^Di. (4)

i = 1

где D_m – суммарный дипольный момент сердца,

D_i – дипольный момент элементарного диполя сердца, вычисленный в ходе решения обратной задачи электрокардиографии.

В ходе решения прямой задачи электрокардиографии по измеренным электрокардиосигналам стандартной системы отведений были определены компоненты вектора дипольного момента сердца D_x, D_y, D_z (см. рис. 2), так как ЭКС представляет собой не что иное, как проекцию вектора дипольного момента точечного генератора сердца на выделенное электрокардиографическое отведение.

Для этого была составлена система из уравнений вида:

Ф j = ^ (cos a Dx + cos pDy + cos уDz) [В], (5) 4л rj                y где Фj(t) — поверхностный потенциал в точке измерения;

• j = 1 … N ;

• Р - среднее удельное сопротивление тела;

D_x, D_y, D_z – проекции вектора суммарного дипольного момента сердца на оси декартовой системы координат;

• а , Р , Y — углы между проекциями вектора суммарного дипольного момента сердца и вектором отведения;

• r_j – расстояние от центра дипольной модели сердца до точек отведений [м];

N – количество отведений.

Система уравнений (5) является переопределенной, в связи с чем, для ее решения был применен метод наименьших квадратов Гаусса, позволяющий находить неизвестные путем минимизации суммы квадратов разностей левой и правой частей уравнений системы.

Полученные кривые дипольных компонент D_x, D_y, D_z в течение кардиоцикла представлены на рисунке 3.

В качестве критерия проверки представленных алгоритмов решения обратной задачи электрокардиографии, авторами выбран следующий - сравнение суммарных дипольных моментов, рассчитанных по формуле (4) D_m по полученным дипольным моментам каждого элементарного диполя сердца, с суммарным дипольным моментом точечного токового диполя D m , расположенного в безграничной однородной среде, вычисленного по компонентам D_x, D_y, D_z .

РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ

Результаты вычислений параметров ЭАС с использованием первого алгоритма приведены на рис. 1 (сплошная линия - суммарный дипольный момент D_m точечного токового диполя, пунктирная линия - суммарный дипольный момент D m многодипольной модели сердца) и рис. 2 (сплошные линии – ЭКС, пунктирные линии – ЭКС, полученный с помощью модели).

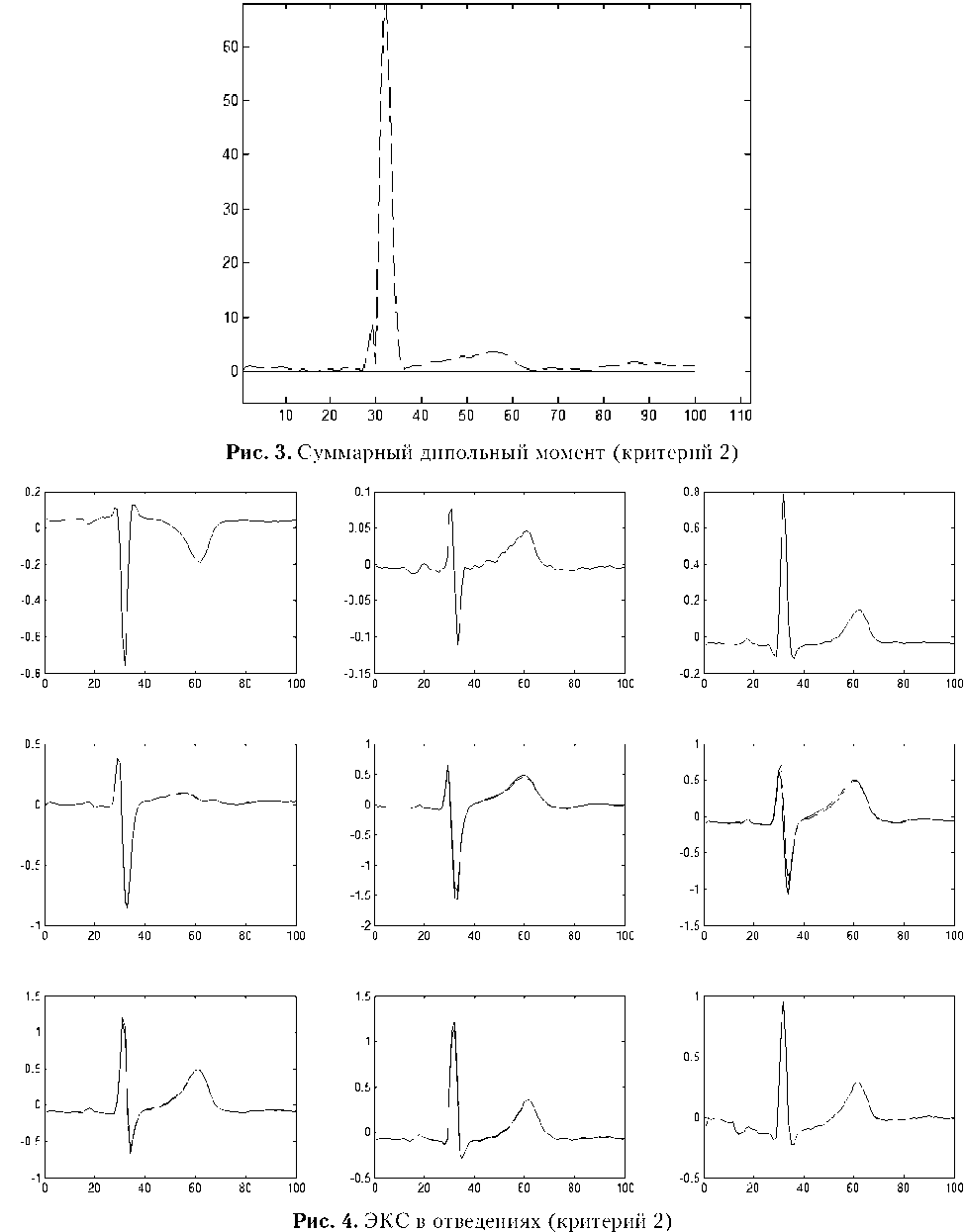
Результаты вычислений параметров ЭАС с использованием второго алгоритма приведены на рис. 3 (сплошная линия - суммарный дипольный момент D m точечного токового диполя, пунктирная линия - суммарный дипольный момент D_m многодипольной модели сердца) и рис. 4 (сплошные линии – ЭКС, пунктирные линии – ЭКС, полученный с помощью модели).

По результатам вычислительных эксперимен-

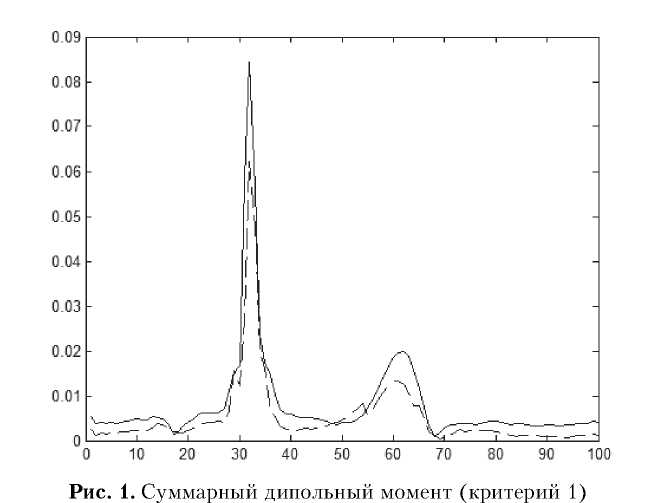
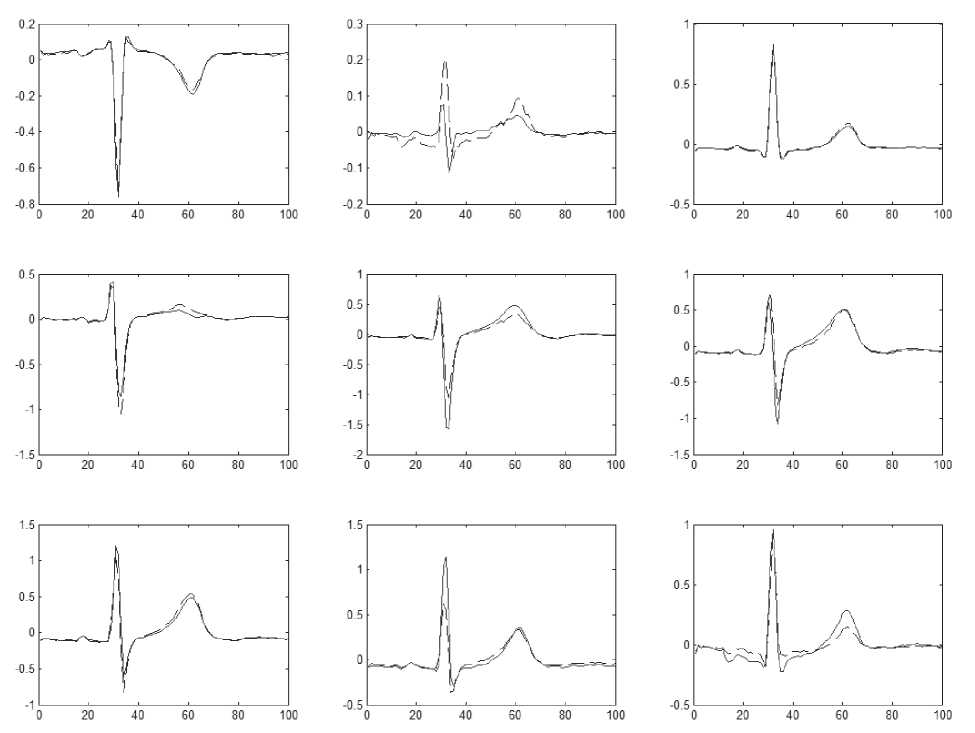
Рис. 2. ЭКС в отведениях (критерий 1)

тов можно сделать вывод, что погрешность восстановления ЭКС в отведениях V1-V6 меньше при использовании второго алгоритма, однако суммарный дипольный момент при найденных дипольных моментах второго алгоритма не соответствует суммарному дипольному моменту точечно- го диполя, который был выбран в качестве эталонного, то есть дипольные моменты с меньшей общей погрешностью, но не отражают физиологических процессов, происходящих в сердце.

Напротив, при использовании первого алгоритма полученные значения дипольных моментов,

с использованием которых синтезируются ЭКС, имеют большую погрешность по сравнению с результатами второго алгоритма. Но при этом более точно были получены кривые суммарного дипольного момента. Несмотря на большую погрешность синтеза ЭКС при использовании первого алгоритма, можно сказать, что полученные дипольные моменты в большей степени отражают происходящие в сердце электрические процессы.

На последнем этапе подхода определения ЭАС возможно осуществление локализации повреждений миокарда на основе анализа полученных значений характеристик ЭАС и визуализация места повреждения миокарда на трехмерной модели сердца. Тем не менее, вопрос поиска оптимального математического аппарата для решения обратной задачи электрокардиографии в предложенной авторами постановке остается открытым.

ЗАКЛЮЧЕНИЕ

В статье описаны результаты исследования двух алгоритмов определения параметров многодипольной модели сердца при моделировании ЭАС. Показано, что первый алгоритм имеет большую погрешность, но позволяет более точно получить кривые суммарного дипольного момента.