Исследование антенных комплексов с использованием киральных метаматериалов и фрактальной геометрии излучателей для систем MIMO

В связи с наличием высококачественного мультимедийного контента, а также увеличения канальной емкости очевидно, что в настоящее время возрастают и требования к качеству обслуживания беспроводных сетей в целом, что, в свою очередь, приводит к их модернизации как программной, так и аппаратной части. Примером такого комплексного подхода является технология MIMO (Massive MIMO) [1; 2], нашедшая широкое применение в современных беспроводных сетях, в т. ч. в сетях IEEE 802.11ax (Wi-Fi 6) и сетях 5G, которая позволяет обеспечить существенное повышение спектральной эффективности. Данная технология используется при многолучевом распространении сигналов, возникающем в том числе в условиях городской застройки.

В работах [3; 4] было показано, что увеличение спектральной эффективности с точки зрения модернизации аппаратной части позволяет обеспечить использование антенных комплексов, в конструкции которых применяются киральные метаматериалы [5; 6]. В общем случае метаматериалы - это искусственные композиционные материалы, представляющие собой совокупность двух и более материалов с кардинально разными элек-

трофизическими параметрами (например, диэлектрик с включенными в него особым образом металлическими вставками). Таким метаматериалам присущи электрофизические свойства, которые нехарактерны для природных материалов и которые обусловлены периодической структурой элементов определенной формы. Среди метаматериалов особый интерес вызывают исследования киральных метаматериалов, в которых проводящие включения зеркально-асимметричной формы равномерно распределены по диэлектрическому контейнеру.

Увеличение спектральной эффективности в системах MIMO путем использования в таких антенных комплексах достигается за счет снижения взаимного влияния между излучателями путем создания высокоомных поверхностей с применением киральных метаматериалов [7; 8].

В современных сетях связи в ряде случаев могут возникать ситуации, когда нескольким радиопередатчикам приходится работать на одну антенну, причем в различных частотных диапазонах. Вместе с тем возникает потребность в многочастотных антеннах, способных функционировать в нескольких частотных диапазонах. Одним из типов таких многочастотных антенн являются антенны и антенные комплексы

с фрактальной (самоподобной) геометрией излучателя [9]. Кроме того, поскольку существует большое многообразие фрактальных геометрических структур, то такие антенны могут выполняться как часть предметов экстерьера, что снижает их заметность, а также может обеспечивать их размещение на объектах (зданиях), где искажение архитектурного облика недопустимо.

В связи с этим настоящая статья посвящена исследованию антенных комплексов с использованием киральных метаматериалов и фрактальной геометрии излучателей для систем MIMO. Излучатели представляют собой фрактальные структуры в виде треугольника Серпинского, кривых Коха и Гилберта, а также дипольной треугольной антенны сложной конфигурации – ФРМ [10; 11], расположенных на подложках из киральных метаматериалов.

	z 11	z 12	•   z 1 n
Z =	z 21 ;	z 22	z 2 n
	. z n 1	z 2 n	. z nn J

В (2) по диагонали матрицы стоят собственные импедансы каждого из входов антенной системы. Недиагональные элементы вычисляются как от-

ношение напряжения, наведенного на пассивном входе излучателя антенной системы к току на активном входе излучателя антенной системы:

U i z j = Ij ’

где U i - комплексная напряженность на пассивном излучателе; I_j - комплексный ток на актив-

ном излучателе.

Для оценки спектральной эффективности си-

1. Методика оценки спектральной эффективности систем MIMO

стемы MIMO с учетом взаимного влияния между излучателями будем условно считать, что корре-

ляция сигналов в парциальных каналах MIMO от-

В работах [3; 4; 12] было показано, что достаточно сильное влияние на спектральную эффективность систем MIMO оказывает взаимное влия-

сутствует, а в источнике и приемнике установлены одинаковые антенные системы. В связи с этим формула (1) записывается как:

ние излучающих элементов антенной системы. Оценить спектральную эффективность системы

С = log 2 det I I +

—q— Z - 1 HZZ ^H H ^H ( z ^{- 1} ) H I ,      (4)

N TX                 J

MIMO с учетом взаимного влияния излучателей

антенной системы предлагается с помощью сле-

дующей формулы [12]:

Г

С = log ₂ det I +— ^zrX X

X HZ_tyRZ H ^h (Z-1 ^ H

TX TX RX

J

где q - уровень сигнала; N_TX - количество парциальных каналов.

Следует отметить, что для обеспечения условия равенства энергетических характеристик системы MIMO необходимо выполнить нормирование матрицы импедансов:

Z norm

,

Z

V tr( ZZ H )

где D_N – суммарная мощность шумов в каждой приемной антенне; Z r_X , Z t_X - матрица импе-дансов приемной и передающей антенных систем соответственно; H – канальная матрица; H ^H – операция эрмитова сопряжения канальной матрицы; R – корреляционная матрица входного сигнала.

Из данной формулы, которая, вообще говоря, является вариацией формулы К. Шеннона [13] на случай системы MIMO, следует, что взаимное влияние излучателей описывается матрицами импе-дансов педедающих и приемных антенных систем, образующих антенный комплекс. Общий вид матрицы импедансов антенной системы, имеющей n излучателя, записывается следующим образом:

где tr( X ) - след матрицы X .

• 2.    Электродинамические модели антенных систем с фрактальной геометрией излучателей, расположенных на киральных подложках

В данном исследовании была рассмотрена система MIMO 2 x 2, в которой были использованы несколько пар фрактальных антенных систем с подложками из киральных метаматериалов (одна приемная, другая, соответственно, передающая). Кроме того, в целях оценки выигрыша спектральной эффективности были также использованы антенные системы с диэлектрическими подложками, относительная диэлектрическая проницаемость которых была положена равной 1 (бc = 1).

Были рассмотрены следующие типы подложек из киральных метаматериалов:

• -    Биизотропные подложки с хаотической ориентацией киральных элементов – спиралей;

• -    Бианизотропные подложки с одинаковой ориентацией киральных элементов – спиралей.

Данные киральные элементы (спирали) были размещены в однородном диэлектрическом контейнере с относительной диэлектрической проницаемостью 1 ( б c = 1 ) . Это связано с тем, что на практике обычно используется материал с небольшой диэлектрической проницаемостью, например пенополистирол.

Важным вопросом является определение резонансной частоты (резонансных частот) кирально-го метаматериала, вблизи которой проявляются данные киральные свойства. Одним из подходов к определению резонансной частоты кирального метаматериала является использование формулы Томсона:

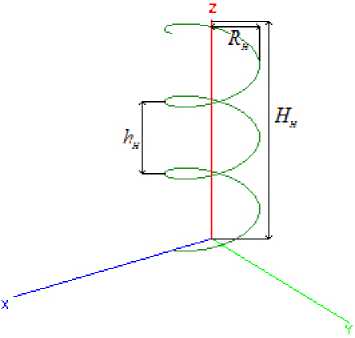
Рис. 1. Cпираль

Fig. 1. Spiral

f 0 2 п VLC

где L – индуктивность киральных элементов; C – емкость элементов.

Рассмотрим одиночную тонкопроволочную металлическую спираль (рис. 1). Данная спираль выполнена из тонкой проволоки, радиус которой составляет Г н . Спираль состоит из Nh витков, расположенных на расстоянии h_H друг от друга, а ее внутренний радиус равен Rh . Длина спирали в развернутом состоянии (длина тонкой проволоки) составляет Н . Высота спирали равна Н н , а угол накрутки - а н .

Для вычисления индуктивности спирали воспользуемся формулой для определения индуктив-

Емкость проволоки спирали вычисляется в соответствии с выражением определения емкости прямолинейного проводника:

C wire =Б0 Б c ----7 ^ ^— IO"⁹,                  (9)

18ln |       | - 1

I Гн J где 1н = 2п(Rh + 2гн)Nh + Нн - длина спирали в развернутом состоянии.

Межвитковая емкость определяется следующим образом:

Sit ( N — 1 )

C it =Б о б с- ^Н ,                            (10)

hH

где S_it

= ^{п (} R H ^{+ 2 Г}Н )    R H ²

- это площадь коль-

ца, образуемая одним витком проволоки.

Расстояние между соседними витками ^ н вычисляется как:

h H =

H _H

N H + ¹.

ности соленоида:

И наконец, межэлементная емкость определяется формулой

L H = ^ц 0 ^ц с

S H N H ²

HH

= W с

^п R H ² N H ² H H

С , elem

=^Б 0 ^Б c k H

S , elem

A 0 ^,

где ц c - относительная магнитная проницаемость 2

среды; Sh = п Rh - площадь витка спирали.

Емкость спирали определяется основными тремя составляющими (8): во-первых, емкостью проволоки C wire , из которой она выполнена; во-вторых, межвитковой емкостью C it ; в-третьих, при наличии группы спиралей, расположенных близко друг от друга, межэлементной емкостью С , : elem

C H = C wire + C it + C elem •                             (8)

N_H ( 2 R_H + 2 r_H )

где Selem =-------7---7---2 rH - плоЩадь про- cos(ан)

странства, занимаемого спиральными элементами; k_H – пространственный коэффициент;

п ан = —-----у - угол накрутки проволоки.

Пространственный коэффициент k_H зависит от расположения и ориентации спиралей. Для случая рассматриваемой биизотропной кираль-ной подложки (когда спирали имеют хаотическую

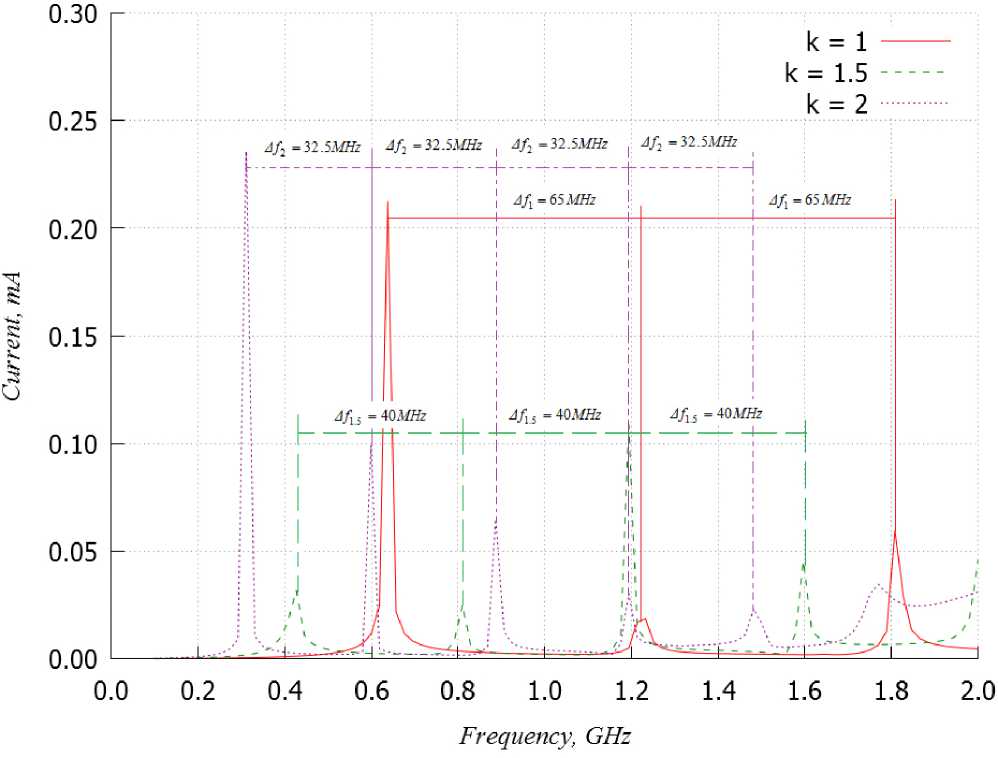
Рис. 2. Зависимость токовой функции спирали от частоты

Fig. 2. Dependence of the current function of the spiral on the frequency

ориентацию и каждую спираль окружают от 3 до 8 спиралей), данный коэффициент был положен равным к н = 0,25.

Подставляя выражения (9), (10) и (12) в (8), получим аналитическое выражение для расчета полной емкости кирального метаматериала на основе спиралей.

Однако формула Томсона (6) определяет лишь первую резонансную частоту кирального элемента. По факту таких резонансных частот может быть гораздо больше. Строгий электродинамический анализ (для расчета токовой функции использовался метод моментов) одиночной спирали, а также кирального метаматериала в целом показал, что в некоторой полосе частот резонансные частоты спирали пропорциональны разности двух близких резонансных частот, т. е. коэффициент пропорциональности равен A f ® f ^ n - f ^ n _- i . В таком случае резонансные частоты определяются в соответствии со следующим выражением:

f 0 n « n A f (13)

При условии допущения определенной погрешности в качестве частоты f ^ n — 1 может быть выбрано нулевое значение, что, в свою очередь, позволяет определить коэффициент пропорциональности как A f ® f ^ . Следует отметить, что формула (13) справедлива для случаев, когда имеет место одновременное пропорциональное изменение высоты H_H спирали и ее радиуса R_H (рис. 2), т. е. f 0 n ~ n A f при к ( H H , R H ) , где к ^е ( 0, +^ю ) •

На рис. 3 приведена электродинамическая модель антенной системы с бианизотропной кираль-ной подложкой, на которой расположен излучатель, представляющий собой диполь Серпинского [10; 11].

Физика работы фрактального излучателя (диполя Серпинского) объясняется тем, что при подключении источника ЭДС к вершине плеча антенны (треугольнику) по нему начинает распространяться электрический ток в направлении его основания. При достижении кластера, размеры которого сравнимы с длиной волны, происходит

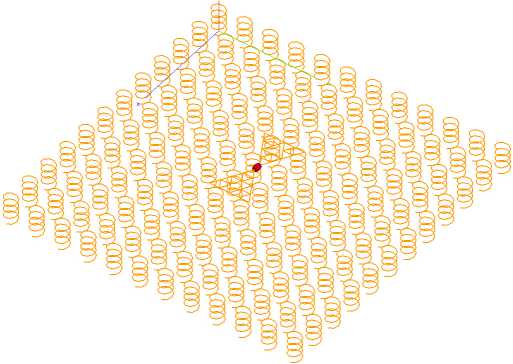
Рис. 3. Модель антенной системы с диполем Серпинского

Fig. 3. Model of an antenna system with a Sierpinski dipole

а

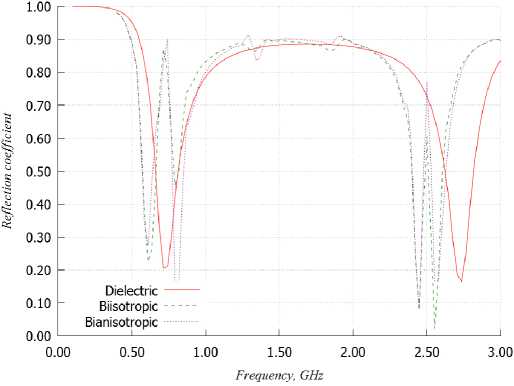
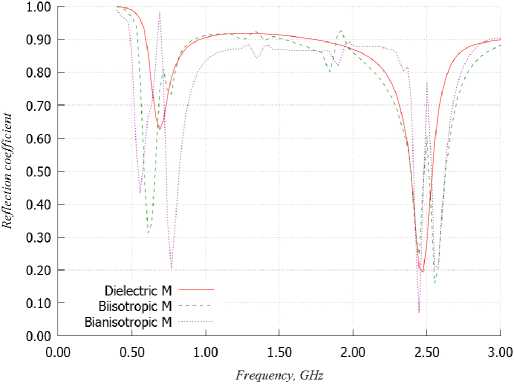
Рис. 4. Зависимости коэффициентов отражения от частоты АСС

Fig. 4. Dependences of reflection coefficients on ACC frequency

б

излучение электромагнитных волн. Аналогичным образом на каждой частоте поверхностный ток локализуется в областях соответствующих по размерам кластеров, в связи с чем антенная система в целом проявляет резонансные свойства каждого такого кластера. Количество кластеров определяется порядком фрактальности. На рис. 3 представлен излучатель, имеющий 4-й порядок фракталь-ности, т. е. разбиение на треугольники происходит за 4 итерации.

На рис. 4 представлены зависимости коэффициентов отражения от частоты антенных систем с диэлектрической, бианизотропной и биизотроп-ной киральными подложками (рис. 4, а ), в т. ч. и металлизированными с нижней стороны (рис. 4, б ), на которых располагается диполь Серпинского (АСС).

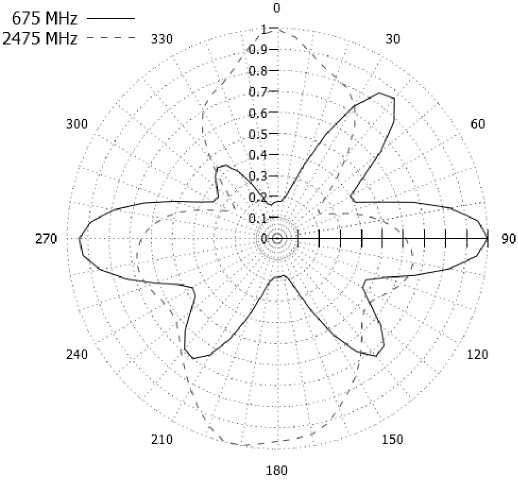
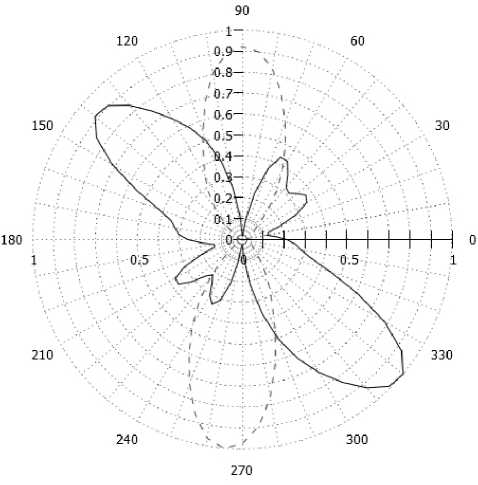
На рис. 5 представлены диаграммы направленности (ДН) АСС с бианизотропной киральной подложкой, выполненной из правовинтовых спиралей, в вертикальной (рис. 5, а) и азимутальной (рис. 5, б) плоскостях.

Как видно из рис. 4, такие АСС работают в двух достаточно сильно разнесенных частотных диапазонах, причем в случае наличия металлизации антенные системы с подложками из кирального метаматериала согласованы гораздо лучше.

Как видно из данных ДН, на нижней частоте 675 МГц такая АСС имеет азимутальное излучение электромагнитных волн, т. е. на частотах резонанса бианизотропной киральной подложки происходит азимутальное рассеяние нормально падающих волн.

На рис. 6 приведена электродинамическая модель антенной системы с биизотропной кираль-ной подложкой, на которой расположен фрактальный излучатель ФРМ.

а

Рис. 5. ДН АСС

Fig. 5. RP of AСС

б

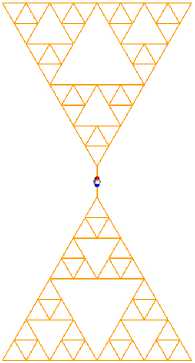
Рис. 6. Модель антенной системы с ФРМ излучателем

Fig. 6. Model of an antenna system with a PRM emitter

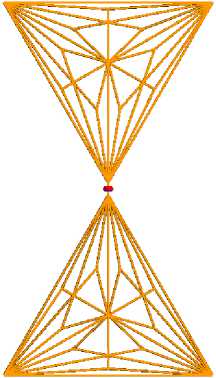
Плечи ФРМ представляют собой треугольники, которые получаются в результате выполнения рекурсивной процедуры (число итераций в данном случае равно 3) соединения центров масс треугольников и их углов (по аналогии с проведением медиан треугольника). Именно благодаря данной аналогии – фрактального разбиения медианами – данная антенна и получила свое название [10; 11].

На рис. 7 представлены зависимости коэффициентов отражения от частоты антенных систем с диэлектрической, бианизотропной и биизотроп-ной киральными подложками, на которых располагается диполь ФРМ (АСФРМ).

Как видно, такой излучатель ФРМ в целом может также работать в двух частотных диапазонах.

На рис. 8 представлены диаграммы направленности АСФРМ с биизотропной киральной подложкой, выполненной из левовинтовых спиралей, в вертикальной (рис. 8, а ) и азимутальной (рис. 8, б ) плоскостях.

Как видно из представленного рис. 8, АСФРМ имеет азимутальное излучение электромагнитных волн уже на двух резонансных частотах.

На рис. 9 приведена электродинамическая модель антенной системы с бианизотропной кираль-ной подложкой, на которой расположен фрактальный излучатель, представляющий собой кривую Гильберта (АСГ).

Следует отметить, что в целях выравнивания потенциалов, что позволяет избежать возникновения

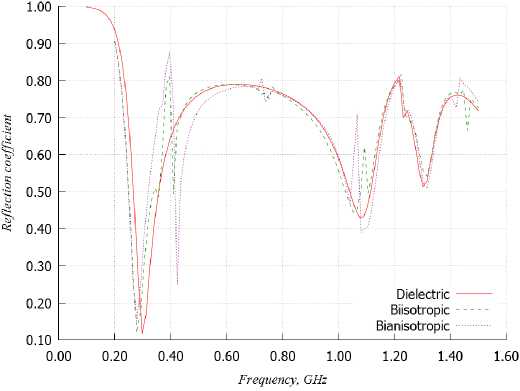
Рис. 7. Зависимости коэффициентов отражения от частоты АСФРМ

Fig. 7. Dependences of the reflection coefficients on the frequency of ASFRM

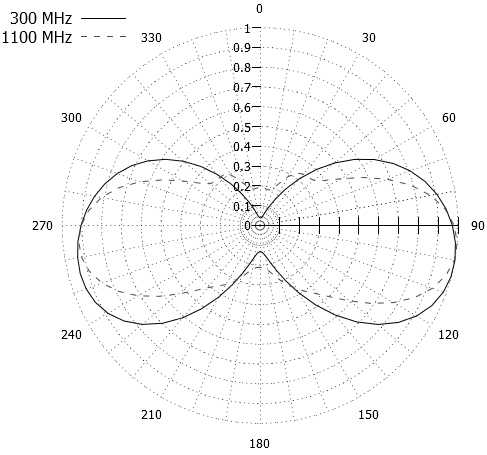
Рис. 8. ДН АСФРМ

Fig. 8. RP of ASFRM

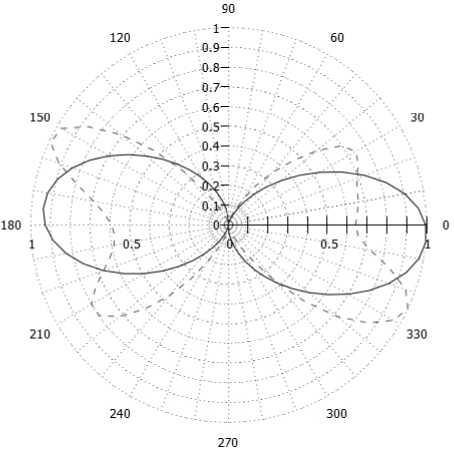
а

б

О О О О О О     ООО о о о о о о      о о о

ООО 000    ОО

ОО   О        о о о о о о о о о о о о о ,о о о о оо

О О О О О ОО о о о оо о о о о о    ос о оо

О О О О О С  ОО)

О О О О О О ОО ) ОО о о о о---

Рис. 9. Модель АСГ с бианизотропной киральной подложкой

Fig. 9. Model of an ASG with a bianisotropic chiral substrate

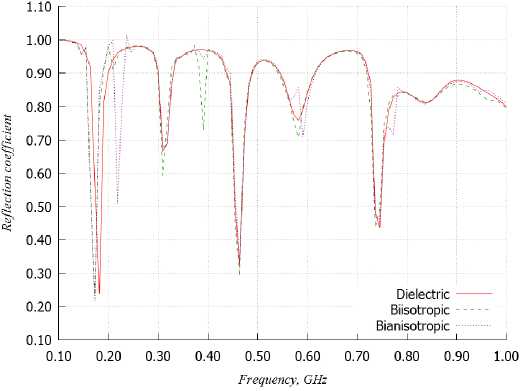
Рис. 10. Зависимости коэффициентов отражения от частоты АСГ

Fig. 10. Dependences of the reflection coefficients on the frequency of the LRA

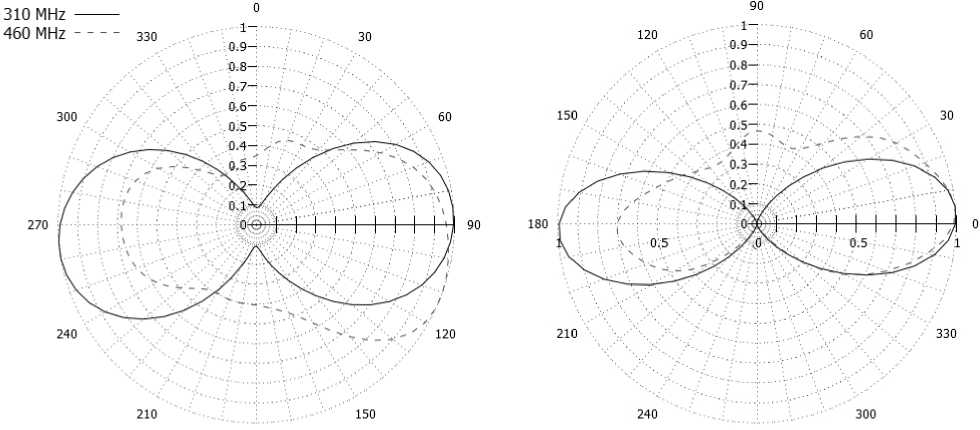
180                                                                         270

а                                                    б

Рис. 11. ДН АСГ

Fig. 11. RP of LRA

противооткатных электромагнитных волн, использовалось шунтовое соединение в нижней части данной антенной системы.

На рис. 10 представлены зависимости коэффициентов отражения от частоты антенных систем с диэлектрической, бианизотропной и биизотроп-ной киральными подложками, на которых располагается излучатель в виде фрактальной кривой Гильберта (АСГ).

Из рис. 10 видно, что АСГ имеет как минимум три резонанса при волновом сопротивлении, равном 50 Ом, однако при другом волновом сопротивлении фидера возможно согласование антенной системы и в других частотых диапазонах.

На рис. 11 представлены диаграммы направленности АСГ с бианизотропной киральной подложкой, выполненной из левовинтовых спиралей, в вертикальной (рис. 11, а ) и азимутальной (рис. 11, б ) плоскостях, рассчитанных на резонансных частотах, в частности на 310 и 460 МГц.

На рассмотренных резонансных частотах так же, как и в предыдущих случаях, имеет место эффект азимутального рассеяния.

И наконец, на рис. 12 приведена электродинамическая модель антенной системы с биизотроп-ной киральной подложкой, на которой расположен фрактальный излучатель, представляющий собой кривую Коха (АСК).

Рис. 12. Модель АСК с биизотропной киральной подложкой

Fig. 12. ASK model with biisotropic chiral substrate

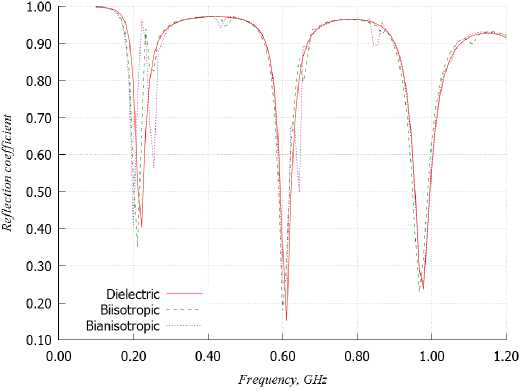
Рис. 13. Зависимости коэффициентов отражения от частоты АСГ

Fig. 13. Dependences of the reflection coefficients on the frequency of the LRA

На рис. 13 представлены зависимости коэффициентов отражения от частоты антенных систем с диэлектрической, бианизотропной и биизотроп-ной киральными подложками, на которых располагается излучатель в виде фрактальной кривой Коха (часть снежинки Коха) (АСК).

В данном случае у такой антенной системы с фрактальным излучателем Коха явно выражены 3 рабочих диапазона частот.

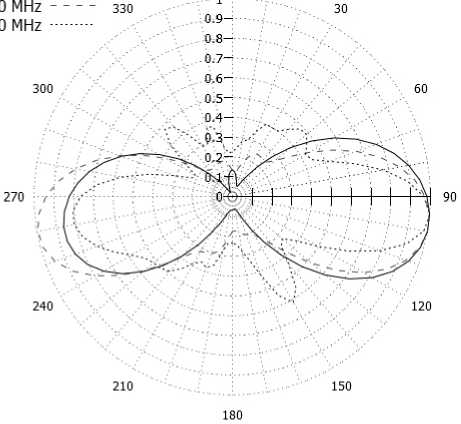
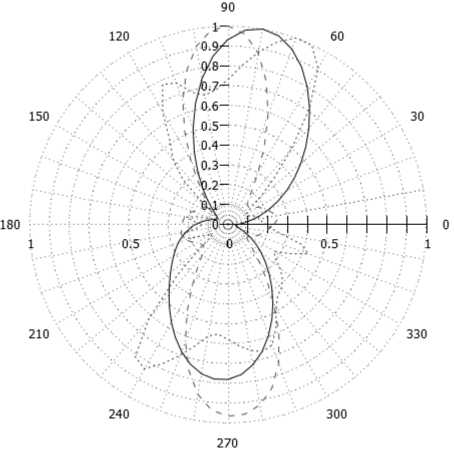
На рис. 14 представлены диаграммы направленности АСГ с биизотропной киральной подложкой, выполненной из левовинтовых спиралей, в вертикальной (рис. 14, а ) и азимутальной (рис. 14, б ) плоскостях, рассчитанных на резонансных частотах, в частности на 220, 610 и 970 МГц.

Во всех рабочих диапазонах, как видно из представленных на рис. 11 диаграмм направленностей, данная антенная с биизотропной киральной подложкой, на которой располагается фрактальный излучатель Коха, обладает азимутальным направлением излучения электромагнитных волн.

• 3.    Оценка спектральной эффективности MIMO систем при использовании антенных комплексов с подложками из киральных метаматериалов и фрактальной геометрией излучателей

Для оценки спектральной эффективности MIMO систем использовались антенные комплексы с подложками из киральных метаматериалов и фрактальной геометрией излучателей. На таких киральных подложках антенных систем параллельно друг другу на фиксированном расстоянии были расположены два фрактальных излучателя различных типов, рассматриваемых выше.

На рис. 15 представлены зависимости спектральной эффективности от частоты при использовании антенных систем с диэлектрической,

220 MHz

а

Рис. 14. ДН АСК

Fig. 14. RP of ASK

б

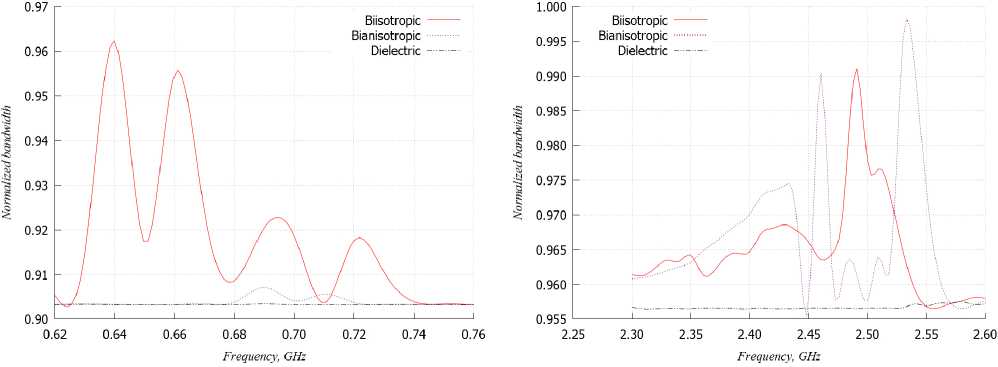
Рис. 15. Зависимости спектральной эффективности от частоты при использовании АСС с различными подложками

Fig. 15. Dependences of spectral efficiency on frequency when using ACC with various substrates

биизотропной и бианизотропной подложками, на которых располагается пара диполей Серпин-ского, а на рис. 16 – аналогичные зависимости с тем лишь отличием, что такие антенные системы располагаются на бесконечно тонкой и идеальной проводящей поверхности (основания).

Как видно из представленных зависимостей, антенные системы на киральных подложках, на которых располагаются диполи Серпинского, могут обеспечить выигрыш в спектральной эффективности по сравнению с антенными системами на диэлектрических подложках, причем в двух частотных диапазонах. В нижнем диапазоне наибольший выигрыш обеспечивают антенные системы на биизотропных киральных подложках, в верхнем диапазоне – как на биизотропных, так и на бианизотропных.

На рис. 17 представлены зависимости спектральной эффективности от частоты при использовании антенных систем с диэлектрической, би-изотропной и бианизотропной подложками, на которых располагается пара фрактальных излучателей ФРМ.

Аналогичным образом такие антенные системы с ФРМ излучателем на киральных подложках обеспечивают выигрыш в спектральной эффективности в двух частотных диапазонах. Однако по сравнению с антенными системами с диполем Серпинского данные АСФРМ, во-первых, обладают меньшей полосой частот, в которой наблюдает-

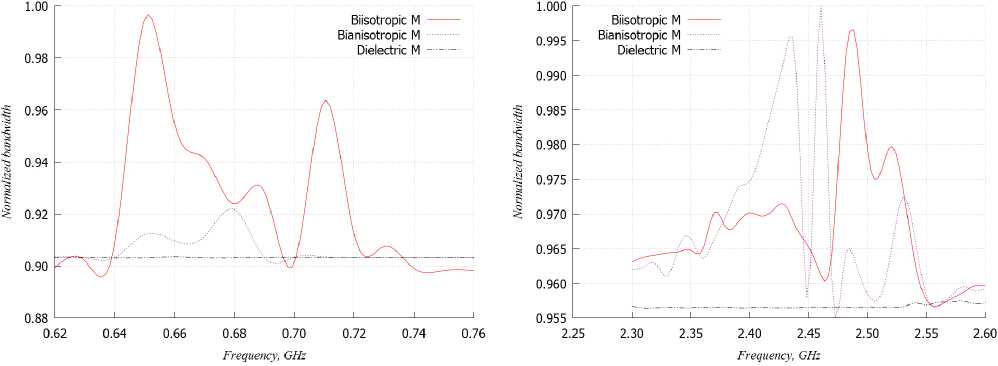
Рис. 16. Зависимости спектральной эффективности от частоты при использовании АСС с различными подложками с односторонней металлизацией

Fig. 16. Dependences of spectral efficiency on frequency when using ACC with various substrates with one-sided metallization

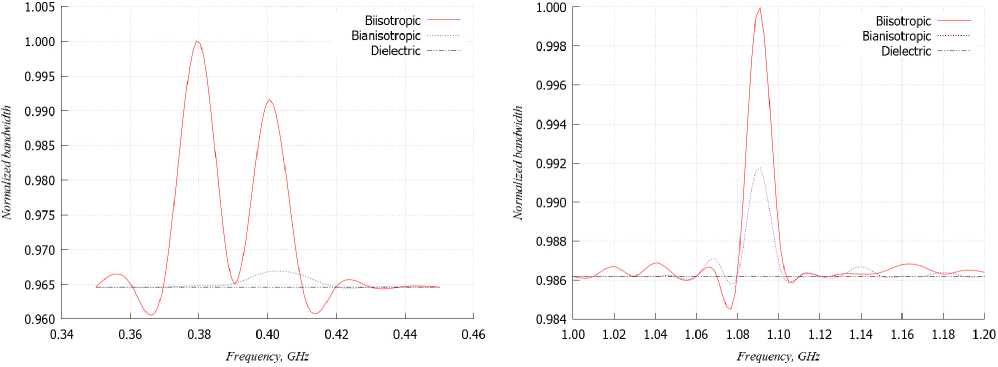
Рис. 17. Зависимости спектральной эффективности от частоты при использовании АСФРМ с различными подложками

Fig. 17. Dependences of spectral efficiency on frequency when using ASFRM with various substrates

ся выигрыш, а во-вторых, гораздо меньшим приростом выигрыша спектральной эффективности.

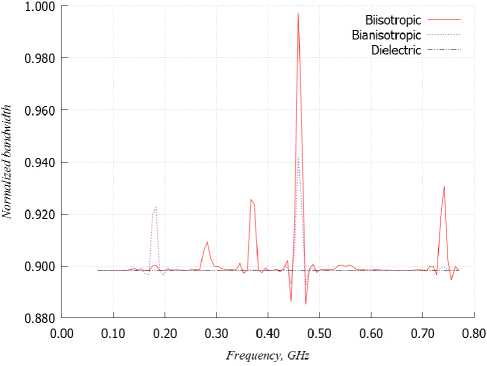
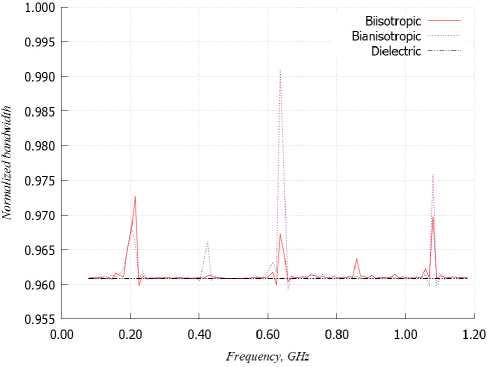
На рис. 18 представлены зависимости спектральной эффективности от частоты при использовании антенных систем с диэлектрической, биизотропной и бианизотропной подложками, на которых располагается пара излучателей, выполненных в виде фрактальных кривых Гильберта (рис. 18, а ) и Коха (рис. 18, б ).

Как видно из представленных графиков, такие антенные системы с излучателями в виде фрактальных кривых Гильберта и Коха в целом позволяют повысить спектральную эффективность в трех небольших рабочих полосах частот. Однако на практике в такой частотной области обычно используются большие по ширине диапазоны, в связи с чем такие решения антенных систем являются весьма специфическими.

Как уже было отмечено, в антеннах с подложками из киральных метаматериалов на резонансных частотах поверхность подложки становится высокоомной, в связи с чем имеет место большее затухание поверхностных волн, что приводит к снижению взаимного влияния излучателей (увеличения развязки между ними), что, в свою очередь, способствует повышению спектральной эффективности.

Заключение

Таким образом, исследование антенных комплексов с использованием киральных метаматериалов и фрактальной геометрии излучателей для систем MIMO позволяет увеличить их спектральную эффективность по сравнению с антенными комплексами на диэлектрических подложках. Следует отметить, что такое решение является весьма специфическим, поскольку обладает относительно небольшой рабочей полосой частот.

а

б

Рис. 18. Зависимости спектральной эффективности от частоты при использовании АСГ ( а ) и АСК ( б ) с различными подложками

Fig. 18. Dependences of spectral efficiency on frequency when using ASG ( a ) and ASA ( b ) with different substrates