Исследование детонационного упрочнения шлифовальных кругов

Нечаев Илья Владимирович, кандидат технических наук, доцент кафедры «Технология твердых химических веществ»

раскрытием зазора в месте прорези при наличии растягивающих напряжений или сближением краев круга в месте прорези при высвобождении остаточных напряжений сжатия. После релаксации внутренних напряжений измеряют начальный зазор х между краями прорези.

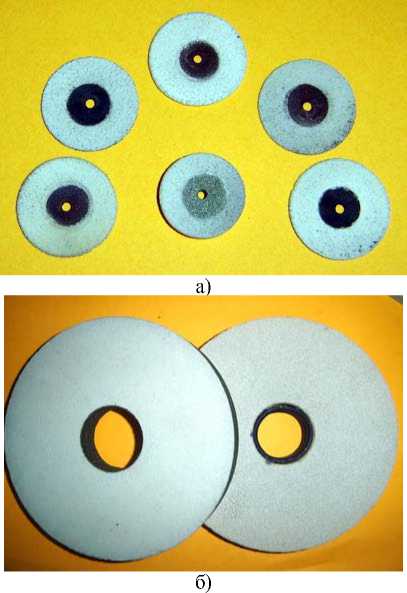
Рис. 1. Примеры упрочнения малогабаритных отрезных кругов (а) и шлифовальных кругов (б). Покрытие – корунд, толщина 100 мкм

После напыления покрытия на боковые поверхности круга зазор между краями прорези приобретает величину x’. Учитывая, что прорезь имеет длину существенно меньше, чем длина окружности неразрезанной части абразивного круга L, можно записать равенства:

- до напыления х = 2 n R - L ;            (1)

- после напыления х ' = 2 n R ' - L ' .

Найдем зависимость, связывающую сжимающие напряжения, возникающие в материале круга под действием формируемого детонационного покрытия, и величинами х и х’ . Для этого рассмотрим элементарный сегмент абразивного круга ABCD (рис. 2), где сплошными линиями очерчен начальный размер сегмента, а пунктирными - размеры сегмента A’B’C’D’ после его сжатия в плоскости рисунка вследствие действия сжимающих напряжений, наводимых покрытием.

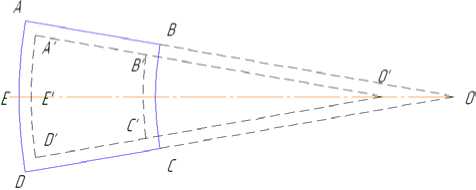
Рис. 2. Оценка остаточных напряжений в материале круга

Из подобия фигур AOE и A’O’E’ следует, что

AO = AO AE ” A' E' .

При этом отрезок АО равен исходному радиусу абразивного круга R, а A’O’ - радиусу круга после напыления R’ . Уменьшение величины сегмента круга АЕ после напыления произошло под действием тепловой деформации круга, определяемой формулой Кингери

AE - A ' E '     . _т —

е =        = аЕ T =

AE        E

, или

A* E* = AE I 1 - — I

I EJ ,

где a - коэффициент линейного расширения материала круга; АТ - разница между начальной Т1 и конечной Т2 (после остывания) температуры покрытия; о - напряжение сжатия круга вследствие тепловой деформации покрытия (сжатия при остывании); Е - модуль упругости материала связки круга. Учитывая, что частицы материала покрытия в момент контакта с напыляемой поверхностью находятся в расплавленном состоянии примем Т1 = Тп (температура плавления материала покрытия). После формирования слоя пятно покрытия быстро остывает до комнатной температуры Тком, поэтому запишем Т2 = Т$ом * 20оС. Аналогично для длины неразрезанной части круга можно записать:

L' = L [1 - — 1

I  EJ

С учетом выражений (2, 3) можно записать:

R' = R [1 - — 1

I EJ

Подставляя (4) и (5) в (1) получим:

х' = 2nR | 1 - — I-LI 1 - — 1 = х I 1 - — I

V E)   ( E J V E)

Выразим из (5) напряжение:

— = E l 1

—

х '

x

Экспериментальную оценку напряжений, наводимых детонационным напылением, выполняли на образцах абразивного круга 100КС315. Для этого на боковую сторону образцов наклеивали алюминиевую пластину с проведенной вдоль пластины (в средней части) царапиной. Разрезали образцы ножовочным полотном шириной ~ 1 мм. Измеряли фактическую ширину прорези (начальный зазор) с точностью 1 мкм. Затем напыляли на боковые поверхности образцов корундовое покрытие толщиной 100, 200 и 300 мкм (вид образцов с покрытием показан на рис. 3). После чего вновь определяли ширину прорези (конечный зазор). Принимая, что модуль упругости материала связки равен Е * 10⁴ МПа, рассчитали напряжения по формуле (6) и усредняли результат.

Рис. 3. Общий вид образцов шлифовальных кругов после напыления

Для оценки ширины прорези перед разрезанием круга на его боковую поверхность наклеивали алюминиевую пластинку, на которой предварительно чертили два перекрестия. Пропил выполняли между этими перекрестиями. Далее место пропила фотографировали с трехкратным увеличением и определяли расстояние между метками с использованием программы BMP.exe.

Результаты оценки изменения ширины зазора (по специальным меткам) после нанесения детонационного покрытий на примере пяти образцов представлены в таблице 1.

Выводы: полученные результаты показали, что за счет напыления корундового покрытия можно создавать в шлифовальном круге остаточные напряжения сжатия, доходящие до 100 МПа.

Работа проводилась при финансовой поддержке Министерства образования и науки РФ.

Таблица 1. Результаты оценки деформации шлифовальных кругов после напыления корундового покрытия

Толщина слоя, мкм	Начальный зазор, мкм	Конечный зазор, мкм	Изменение зазора, мкм	Количество слоев напыления
100	1087	1053	34	7
100	1125	1094	31	7
100	1090	1062	28	7
100	1125	1089	36	7
100	1148	1114	34	7
200	1093	1025	68	13
200	1115	1044	71	13
200	1112	1055	57	13
200	1096	1037	59	13
200	1077	1018	59	13
300	1109	1005	104	20
300	1110	1011	99	20
300	1108	1012	96	20
300	1092	998	94	20
300	1101	1004	97	20