Исследование диэлектрических свойств водного раствора иодида лития с учетом обобщенной потенциальной энергии взаимодействия

DOI:

Известно, что структура воды и водных растворов электролитов с физико-химической точки зрения определяются пространственно-временным распределением структурных единиц раствора и их взаимодействия. На структуру растворителя влияют специфические особенности распределения и взаимодействия ионов растворяемого вещества, что приводит к изменению физико-химических параметров растворов [2; 7; 17; 20; 21]. Следовательно, свойства и структура водно-электролитных систем определяются пространственным расположением их структурных единиц, что важно для предварительного знания механических, тепловых, электрических, диэлектрических и магнитных свойств. Например, в первой области концентраций структура воды является матрицей, на которой развиваются взаимодействия в растворах [5; 6]. В этом случае в единой структуре наблюдаются геометрические и объемные соответствия конфигураций ионов и растворенных молекул. В области высоких концентраций фрагменты гидратных сфер, ионные и водные кластеры комплементарно связаны между собой, что со структурных позиций создает условия повышенной смесимости компонентов. При этих концентрациях установлены и реализуются структурные переходы для большого числа модельных растворов. Они подтверждаются макроскопическими физико-химическими и микроскопическими методами, а также моделированием, методом молекулярной динамики (МД) и методом интегральных уравнений (ИУ) для модельных растворов, что наблюдается специфика концентрационного перехода водно-электролитных систем [23–25]. В этих работах установлены отличия диэлектрической проницаемости, время релаксации и активности воды растворов электролитов в разных концентрационных зонах. В рамках общей схемы рассмотрены закономерности, определяющие влияние структурно-кинетических изменений воды в разных концентрационных зонах растворов, а также на их термодинамические и диэлектрические свойства.

В работах [3; 4; 19] исследованы изменения комплексной диэлектрической проницаемости и релаксации водных растворов иодидов лития, калия и цезия в широком интервале изменений концентрации и температуры в области частотной дисперсии диэлектрической проницаемости воды. Изучены динамические коэффициенты диэлектрической проницаемости и потери этих растворов при изменении температуры от 288 до 323 К в интервале частот от 7 до 25 ГГц. Измерены их низкочастотная электропроводность и рассчитаны ионные потери на высоких частотах. В растворах наблюдается одна область релаксации, описываемая уравнениями Дебая или Коула — Коула. Также в работе [19] изучены зависимость времени диэлектрической релаксации τи статической диэлектрической проницаемости e _s водного раствора электролита литий иодида от температуры и концентрации. Здесь отмечается, что время и энтальпия активации процесса диэлектрической релаксации уменьшаются при переходе от воды к растворам, что соответствует нарушению исходной структуры воды и повышенной подвижности молекул воды в гидратных оболочках ионов [19]. В начальной области концентраций наблюдается линейная зависимость активности воды от 1/e _s . При высоких концентрациях статическая диэлектрическая проницаемость e _s растет с увеличением температуры. В связи с широким применением этих растворов в медицине и производстве фотореактивов, представляют большой интерес также теоретические исследования этих свойств водных растворов электролитов.

В работах [10; 13–16] методом кинетических уравнений получены аналитические выражения для коэффициентов диэлектрической проницаемости е1(ш) и диэлектриче- ских потерь е1(ш), где в подынтегральных выражениях для потенциальных частей содержатся энергия взаимодействия Фа0(г) и радиальная функция распределения дОлИ. На основе полуфеноменологической асимптотической модели раствора [20], которая описывается в приближении теории Мак-Миллана — Майера, где растворитель предполагается сплошной средой и в нем имеет место тепловое движение ионной подсистемы, проведены численные расчеты коэффициентов трения ионов ва, во, трансляционных та, то и конфигурационному таЬ временам релаксации, а также коэффициентов е1(ш) и е2(ш) водных растворов LiCl, NaCl, KCl, CsCl и KF. Здесь вклад растворителя в значение коэффициентов диэлектрической проницаемости е1(ш) и диэлектрических потерь е2(ш) водных растворов электролитов учитывается посредством статического значения коэффициентов диэлектрической проницаемости растворителя ess, а также коэффициентами трения ва и вь ионов сорта а и b [10; 13-16]. Однако согласно [1; 9; 11; 12; 20] энергия взаимодействия между структурными единицами ионно-молекулярных систем состоит из суммы межионных, ионно-дипольных и диполь-дипольных потенциалов взаимодействия, которая учитывает их вклад в коэффициенты диэлектрической проницаемости и электропроводности растворов электролитов, что является важным.

Целью работы является проведение численных расчетов и изучение частотной дисперсии коэффициентов е 1 (v) и e 1 (v) с учетом вклада обобщенной энергии взаимодействия для водного раствора электролита иодида лития, в зависимости от температуры Т , плотности р и концентрации С и частоты v.

Основные выражения и выбор модели раствора

В работе [12] на основе обобщенного потенциала взаимодействия ионно-молекулярных систем, учитывающих в некоторых приближениях вклад ион-ионных, ион-молекулярных и межмолекулярных взаимодействий, исследованы частотная зависимость коэффициентов диэлектрической проницаемости е 1 (v) и диэлектрических потерь e ₂ (v) водного раствора калия иодида. Получены аналитические выражения коэффициентов диэлектрической проницаемости e 1 (v) и диэлектрических потерь e ₂ (v) с учетом обобщенного потенциала для ионно-молекулярных систем и проведены численные расчеты этих коэффициентов в зависимости от температуры Т , плотности р, концентрации С и частоты ν для растворов иодида калия, а также построены диаграммы Коула — Коула.

В качестве исходного принимаем аналитические выражения коэффициентов диэлектрической проницаемости е 1 (ш) и диэлектрических потерь е ₂ (ш) с учетом обобщенного потенциала ионно-молекулярных систем, когда потоки затухают по экспоненциальному закону, которые получены в [12] и имеют следующий вид:

, _       л-⁰т_                  (1 — :.,, ²)

'^ -'■+— ео (1 ■'■ 11 + — 1 + .2 й )2Лаь(0)|'

V (шТ^О^Т а     ^{5    (1} + ^ )

'' V . . (ШТ„)2)11 + V 1 + .= ' ^)2Л“<0)1’( )

а                                    о где

Л„0(0) - 2п х пй„о■“52^ — 9-2^ци^'^1^д^Г’(3)

m _a m _b

^T a = D O , ^T b = о О , ^T ab =

2 P a        2 в Ь

dlb   вавь кТ (ва + вь) ’

глубина потенциальной ямы энергии межчастичного взаимодействия; R _ab =

X* = Xabdab — приведенный обратный дебаевский радиус экранировки, в котором согласно [22] x определяется в виде х2 = Z2a е Хкт, а Uab(r, 0, ф) — потенциальной энергией взаимодействия диполей; U*b(r) = МХ^+^М-)), UiS(r) = ^(Za+Jib)e^-2 — потенциальная £s®aab энергия ион-дипольного взаимодействия; Uss(r) = ^X X — потенциальная энергия essdab - диполь-дипольного взаимодействия; L(Uab(r)) = [cth Uab(r) — ^*1(-) ] — функции Ланже- вена, sh(Ua*b(r)) и cthU*b(r) — гиперболические функции; ess — коэффициент диэлектрической проницаемости растворителя; dab = (daa±dbb), f = ^Л—; е0 — электрическая постоянная; ц — электрический момент молекулы-диполя и ц2 = p.s^s; У,Ь(г) — ради-ф*Ь Л)

альная функция распределения, которая согласно [20] ^ab(r) = У(r, Р*)е н ; У^ Р*) — бинарная функция распределения двух полостей, где ограничимся ее контактным зна- чением ^(r, р*) ^ ^(р*) на расстоянии r = 1 (rab = dab), полученная Карнаханом —

(2 - р * ) n nd3, np d3, No

Старлингом в виде ^(р*) = 2(1—Р*)3, Р* = —g = —6м— — приведенная плотность; р — плотность раствора; N0 — число Авогадро; М — молярная масса; ст, = "“Х0,, п* = n^bdab, Qab = П (ХХ+м), ma, mb — массы; ea, eb — заряды; ^a, пь — числовые плотности; da, db — диаметры; во,, вь — коэффициенты трения ионов сорта а и Ь; е — элементарный заряд; za, zb — валентность ионов; Ta, Tb и Tab — времена релаксации в импульсном и конфигурационном пространстве; rab = qb — qa — взаимное расстояние; r = d^ — приведенное расстояния между ионами сорта а и Ь; е0 — электрическая постоянная; к — постоянная Больцмана; Т — абсолютная температура; ш = 2nv — циклическая частота; v — частота процесса; е^ — значение коэффициента диэлектрической проницаемости при ш ^ то.

В дальнейшем возникает необходимость учета малых параметров, то есть когда U a_b (r) = Хт) <<  1 и это всегда имеет место. Если обсудим даже по классической теории электропроводности, то исходя из представлений о свободных частицах (ионах) электролитов предполагается, что ионы проводимости в электролитах ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершенно свободно и эти столкновения приводят к установлению теплового равновесия системы (полуфеноменологическая осмотическая модель раствора, которая согласно [1; 3–7; 9–16; 18–25; 25] описывается в приближении теории Мак-Миллана — Майера). Отсюда, для упрощения этих выражений учитываем условия малых параметров, разлагая в подынтегральных выражениях функции Ланжевена L(U a_b (r)) и гиперболические функции sh(U< * _b (r)) и cthU< * _b (r) в ряд и ограничиваясь линейными членами. Тогда выражение (3) принимает следующий вид:

Л о» (0) - 2п х п*,. /“[2 2 1 * 12 ) — аад ^U^]_g>)r 2 dr.       (5)

Таким образом, формулы (1) и (2) в контексте (5) позволяют исследовать частотную дисперсию коэффициентов диэлектрической проницаемости e i (v) и диэлектрических потерь e ₂ (v) с учетом обобщенного потенциала ионно-молекулярных систем в зависимости от термодинамических параметров состояния. Как и в работах [1; 9; 11; 12], в этих выражениях потенциальные члены определяются обобщенным потенциалом энергии взаимодействия, который состоит из суммы межионных, ион-молекулярных и межмолекулярных потенциалов взаимодействия, а также радиальной функции распределения 9 a, (r), и при определенном выборе модели раствора эти равновесные структурные параметры известны в литературе. В дополнение к сказанному вклад растворителя в коэффициенты диэлектрических параметров учитывается посредством статического коэффициента диэлектрической проницаемости растворителя e _ss , коэффициентами трения в _а , в , ионов сорта а и Ь.

Для проведения численных расчетов коэффициентов диэлектрической проницаемости е 1 (ш) и диэлектрических потерь е ₂ (ш) водного раствора электролита иодида лития с учетом обобщенного потенциала взаимодействия наряду с известными молекулярными параметрами m _i , e _i , п^ d i (г = а, Ь) еще понадобится определение коэффициентов трения в _а , в , трансляционных т _а , т _ь и конфигурационному т _аЬ временам релаксации.

Далее аналогично коэффициентам диэлектрической проницаемости е 1 (ш) и диэлектрических потерь е ₂ (ш) при вышеприведенных условиях в [12] для выражения коэффициентов трения в _а , в , частиц сорта а и Ь получены следующие выражения:

в а = Е 4^ Е da, /“ I ^Ц^ - l^) а                Ь        ⁰

9 2 ^и»  2 эи ;_ь (г)   ^{2 U} „> ) 7/_г(^и»)

х 1 -д72_ + 7”а7      72“11 ц» 911(7)7 dr, в2 = Е     Eda, / “I      2     -ЬЮ a2ua,(r)  2 эи;„(т)  ж,» <»

х 1   ..    + 7^7          ••   11   ua,(r) 9a,(r)r dr’ которые также полностью учитывают вклады взаимодействия структурных единиц, то есть межионные, ионно-молекулярные и межмолекулярные взаимодействия.

Следует отметить, что для проведения численных расчетов полученные выражения коэффициентов трения в _а , в , в виде (5) являются сложными. Поэтому, как выше, разлагая в подынтегральных выражениях функции Ланжевена L(U a_b (r)) и гиперболические функции s^(U a, (r)) и cthU a, (r) в ряд и ограничиваясь линейными членами, получим аналитическое выражение коэффициентов трения в _а , в , в следующем виде [12]:

„2   v-⁴ n             Г ,д 2 Ф 7 0 (г)

^ва = 52 "3" ^{Р а} ^^т 52 ^{d ab} У_о^[ а72

-

+ 2 а Ф а ; (r) - u g_t <7) _х r dr        3

^д 2 ^и :, (г)    ^{2 au} :, (r)     ^{2 u} :, (r)

^{х 1}   _дг 2    ⁺ 7^7       72”U⁹ ab^{( r ) r dr},

2 v-⁴ n            Г Э 2 Ф^ (г)

^{в —} 52 у^ръ^^Т 52 ^ ^аь у_о [ дт 2

+ 2 Э ф*0 (г) —   * х т Эт        3

—

х |  '  + 2■  — 2^

Эт 2 т Эт         т ²

Следует отметить, что в выражениях (3), (5)–(9) расстояния между структурными единицами раствора характеризуются через приведенное расстояние т — У, где dab таЪ — дъ — да — межчастичное расстояние, а dab — (daa+dbb) — расстояния между центрами двух ионов раствора, когда столкновения считаются упругими (т — 1 (таЪ — d^)) и при взаимодействии структурных единиц раствора центры двух частиц сближаются на этом приведенном расстоянии т. А если соударение между ними неупругое, то молекулы немного деформируются и это соответствует примерно 0, 9т. Отсюда предел интегрирования при расчетах дается примерно от 0, 85т-0, 95т (нижний предел) до 10т (верхний предел), что соответствует тому, что расстояние между взаимодействующими частицами раствора 10daЪ.

Численные расчеты и обсуждение результатов

На основе формул (8) и (9) произведен численный расчет коэффициентов трения в _а , в _Ъ , а также согласно определению времен релаксации т _а , т _ъ и т _аЪ ионов в зависимости от термодинамических параметров состояния. А потом с учетом численных расчетов этих коэффициентов трения и времен релаксации и на основе формул (1)–(2) и (5) рассчитаны частотные дисперсии коэффициентов e 1 (v) и e ₂ (v) для водного раствора электролита иодида лития в зависимости от плотности р, концентрации С , температуры Т и частоты v. Численные расчеты проведены программным пакетом «Mathematica 8». Полученные результаты приведены в виде таблиц и рисунков.

В таблице 1 отражены численные значения коэффициентов трения в _а , в ъ > времен релаксации т _а , т _ъ и т _аЪ , а в таблицах 2-4 — коэффициентов диэлектрической проницаемости e 1 (v) и e ₂ (v) диэлектрических потерь водного раствора электролита иодида лития при температурах 283-353 К, в интервале изменения концентрации 1 <  С <  7 моль/кг, плотности 1107 <  р <  1517 кг/м ³ и диапазоне частот 7, 5 <  v <  10 4 ГГц. Проведены сравнения полученных теоретических результатов с экспериментальными данными работы [19]. Ход концентрационной, плотностной и частотной зависимости e 1 (v) и e ₂ (v) соответствует экспериментальным результатам.

Известно, что диэлектрические свойства растворов электролитов характеризуются коэффициентами диэлектрической проницаемости и диэлектрических потерь, которые связаны релаксационными процессами в растворах. При оценке этих коэффициентов разные авторы используют разные выражения времени релаксации. Например, наши численные расчеты отличаются от других теоретических и экспериментальных данных тем, что при выборе модели раствора у нас имеются два времени релаксации (выражения 4), то есть трансляционное время релаксации ионов т _а , т _ъ и конфигурационное (то есть «структурное») время релаксации т _аЪ , численные значения которых приведены в таблице 1 для температуры 298 К при разных концентрации и плотности.

Таблица 1

Численные расчеты коэффициентов трения ( β ₁ , β ₂ ) и времен релаксации ( τ ₁ , τ ₂ , τ ₁₁ , τ ₁₂ , т ₂₂ ) водного раствора LiI в зависимости от плотности р и концентрации С при Т = 298 К

С, моль/кг	р , кг/м 3	в 1 , 10 - 14 кг/с	в 2 , 10 - 14 кг/с	Т [19] , 10 - 12 с	Т 1 , 10 - 12 с	Т 2 , 10 - 12 с	Т 11 , 10 - 12 с	Т 12 , 10 - 12 с	т 22 , 10 - 12 с
1	1 107	1,187	6,138	7,1	0.,490	1,718	0,122	0,331	1,505
2	1 208	1,705	9,063	6,2	0,341	1,164	0,176	0,478	2,221
3	1 273	1,998	10,755	5,7	0,291	0,981	0,206	0,561	2,636
4	1 342	2,291	12,467	5,3	0,254	0,846	0,236	0,644	3,056
5,5	1 439	2,691	14,824	5,0	0,216	0,712	0,277	0,758	3,634
7	1 517	3,005	16,685	5,1	0,193	0,632	0,309	0,848	4,090

Как видно из таблицы 1 и рисунка 1, коэффициенты трения и времен релаксации в конфигурационном пространстве ионов сорта а и b зависят от концентрации, и изотермически при увеличении концентрации возрастают. Однако зависимость трансляционная (т 1 , т ₂ ) и диэлектрическая (т ₂ ) времена релаксации ионов, согласно численным расчетам и экспериментальным данным [19], по возрастанию концентрации и температуры уменьшается (см. рис. 2), что соответствует ранее полученными данными для других водных растворов [1; 9–16].

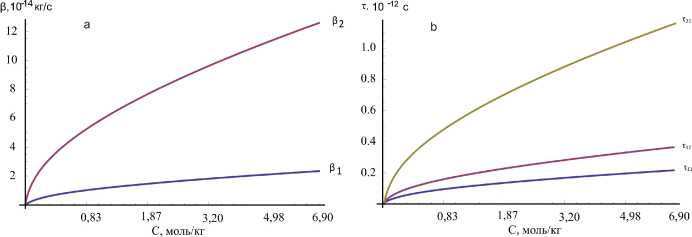
Рис. 1. Зависимость коэффициентов трения (а) и времени релаксации (Ь) ионов в конфигурационном пространстве от концентрации при температуре 298 К

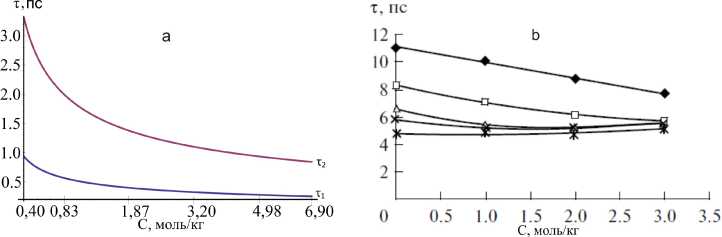
Рис. 2. Зависимость времени релаксации ионов водных растворов электролитов иодида лития от концентрации: а) трансляционных времен ( т 1 , т ₂ ) релаксации при температуре 298 К по численным расчетам; b) время ( т ₂ ) диэлектрической релаксации при температурах ^ 288, D 298, △ 308, х 313, * 323 К по данным [19]

Таблица 2

Зависимость статического коэффициента диэлектрической проницаемости 6 _S водного раствора иодида лития от концентрации и температуры

т,к	288	288	298	298	303	303	313	313	323	323
С ,моль/кг	[19]	Расч.	[19]	Расч.	[19]	Расч.	[19]	Расч.	[19]	Расч.
Вода	82,1		78,4		74,9		73,2		69,9
1	67,8	62,95	63,0	60,58	61,0	59,44	59,5	57,25	57,5	55,18
2	55,1	55,25	52,4	53,19	51,6	52,21	50,5	50,32	49,8	48,54
3	45,8	50,22	44,7	48,37	45,2	47,48	45,6	45,77	44,7	44,17
4	38,6	44,83	38,5	43,18	40,2	42,40	41,4	40,91	40,1	39,49
5,5	30,9	37,08	32,7	35,74	35,3	35,10	35,4	33,90	35,8	32,77
7	27,0	30,80	28,9	29,69	31,8	29,17	31,9	28,23	33,5	27,31

8i(v), 82(v)                                                         8i(v),8₂(v)

10           100         1000      10000            1           10          100         1000        10000

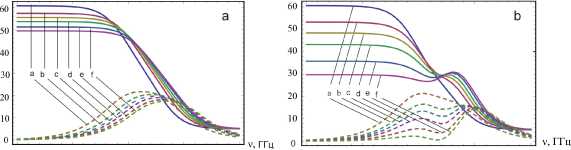
Рис. 3. Частотная зависимость коэффициентов диэлектрической проницаемости 6 1 ( v )

( сплошная линия ) и диэлектрических потерь 6 2 ( v ) ( штриховая линия ) водного раствора LiI при температуре 298 К и разных концентрациях:

а — 1; b — 2; с —3; d — 4; е — 5,5 и J — 7 моль/кг;

a ) без потенциальной части формулы (1)–(2); b ) с учетом потенциальной части формулы (1)–(2)

Рис. 4. Диаграмма Коула — Коула для водного раствора LiI при температуре 298 К и концентрации (моль/кг): а — 0 (вода); b — 1; с — 2; d — 3; е — 4; f — 5,5; д — 7. а ) по данным [19]; b ) расчетные данные без потенциальной части формулы (1)–(2);

c ) расчетные данные с учетом потенциальной части формулы (1)–(2)

На рисунке 3 приведены частотная дисперсия коэффициентов диэлектрической проницаемости 6 1 (v) и диэлектрических потерь 6 2 (v) водного раствора LiI при Т = 298 К и разных концентрациях, без учета потенциальной части (а) в выражениях (1) и (2), которые соответствуют трансляционному движению ионов сорта а и Ь, также с учетом потенциальной части (b), обусловленное взаимодействием ионов и диполей. Как видно из рисунка 3а, для 6 1 (v) и 6 2 (v) имеется одна область частотной дисперсии, приблизительно равной 10 2 Гц, а на рисунке 3b — две области дисперсии, обусловленные ионами и диполями. Аналогичное явление имеется на диаграмме Коула — Коула, где на рисунке 4b — одна область частотной дисперсии, а на рисунке 4c — две области, когда первая область относится к диполям, а вторая — к ионам.

Таблица 3

Зависимость изотермических коэффициентов диэлектрической проницаемости 6 1 ( v ) и диэлектрических потерь 6 2 ( v ) водного раствора LiI от р , С и v при = 298 К

О	ш	у о СО CU	CD CD	oq ^	о ID	ОО СО^ ID	о ID	CD CD ^"
	ш	У о СО CU	ОО D ОО	СО СО^ со	ID	oq ^	ОО О)"	^ CO^ oq
о	ш	У о СО CU	ОО оо~ ОО	СО СО^ cd"	со оо~ CD	о"	CD ш"	GO oo"
	ш	У о СО CU	CD О) 5	о §	ОО СО	о in СО	oq со	^p oq
S	ш	У о СО CU	ОО ио CD"	о	Ш СО Оо"	^	oq ^	§
	ш	У о СО CU	^ оо" d	oq lO GO ^	оо ’ф		оо оо^ со" СО	co GO OO
d ОО	ш	У о СО CU	CD оо"	СО LO CD	CD lO	^ ОО^ со"	Ш СО оо"
	ш	У о СО CU	ш СС ш	ОО CD Ш	GO СО ^	^ оо" ^	CD оо^ ш" СО	oo ^ oo" oo
		О?	LQ	СО ОО	оО cd" оо	ОО^ ^ oq	со" оо	oo^ oo
CD	ш	у о СО CU	1D CD	ОО ОО ^	СО со"	LO оо"	^ LD	CO
	ш	У о СО CU	^ 1D оо"	ю CD оо" ш	CD О) ^	ОО оо"	^ 1D m" CO	CD 1D oo oo
		О?	^ ОО ^	оо^ О©" СО	ID СО	СО	o^ oq	CD ^ OO
1D	ш	у о СО CU	ОО со	СО оо"		oq оо^	co	m CO^
	ш	У о СО CU	Ш ОО S	СО" ш	GO оо^ СО	oq со" ^	OO CD iD CO	CD O^ OO
		о?	оо^ CD" lQ	CD cd"	5	СО	^	CD^ oq
ю	о.		О	ОО оо	СО оо	oq ^ СО	OO CO ^	uO
	и	ьО ^ О 5	’—1	оо	СО	^	in in	b-

О	Ш	о CO CU	CD oo"	OO oo^	CO °4	CD CD^	^	CD	CD	CD oo~	CD OO^ Oo"
	Ш	T о CO CU	m CD^ oo"	CO CD^ oo"	CD^ Oo"	OO D OO	^ D^ Oo"	^ Oo"	CD ^t Oo"	D D OO	CO Oo"
о	Ш	T о CO CU	CD CD^ oo" oo	oo" oo	OO CD^ oq	OO oo~ oq	oq D S	OO °4 oo"	О Oo"	CO ^	^ cd"
	Ш	T о CO CU	CD oo"	oo"	LO	CD OO^ 9	CO CD^ Oo" CO	CD oo~ oo" CD	OO cd" CO	oq cd" cd	^ d" CD
s	Ш	T о CO CU	CD °1	oo	о	OO D CD"	D d"	CD D d"	s	CO oo~ co"	OO oo"
	Ш	T о CO CU	CD m" m	CD oo~ ^ m	LO co" D	^ oo" D	D D	CO OO^ oo"	CO D cd"	oo D d"	oo °4 co"
m oo	Ш	T о CO CU	о	oo OO^	О	CD Oo"	CD OO^ oo"	oo"	CO D^ cd"	CD D	CD oo~
	Ш	T о CO CU	^ CD	CO OO^ s	CO oo~ oo" D	D cd" D	CD D	D	CD CO D	CD Oo"	oo °4
		oT		in co" oo		D D	oo^ CD CO	°4 CO	°4
CD	Ш	t о CO CU	oq	oo^ CD	CD	D CD	CD	oo d"	D D d"	о d"	oo ^
	Ш	T о CO CU	О co" CD	°4 CD	CD CD^ S	^h D Oo" D	CO D	CO D cd" D	oq ^ D	oo ^ D	^h °4 cd"
		oT		^t cd" CO		^t co"	D GO	Oo"	D^ D
UO	Ш	t о CO CU	^ CO	OO^ CO~	oo^ CO~	oq CO~	^ OO^ oo'	CD °4 oo"	oo"	OO ^ oo"	oo oo~ oo"
	Ш	T о CO CU	^h co" CD	oo" CD	D CD	1D D S	GO D	о D	OO oo^ ^ D	CD D	oo D Oo"
		o?		co" Ю		OO^ cd" D	D	CD^ D	D
^f	Cl	^	о	о	О	О	О	О	§	CD О	oo о
		ti	CO CD OO	CD CD OO	CO OO OO	CD OO OO	CD CO	CO CO	CO OO CO	CD ^h CD	CD D CD

Как видно из таблицы 1 численных значений, время релаксации водного раствора иодида лития по данным [19], который по ходу изменения концентрации и плотности соответствует нашему трансляционному времени релаксации, приблизительно на 1 порядок больше. Например, у эксперимента равно т = 7,1 пс (одну область дисперсии), а наша модель раствора т 1 = 0,49 пс, т 1 = 1, 718 пс (за счет чего и появляется две области дисперсии) (см. рис. 3 и 4). Поэтому при выполнение условия шт = 2nvT = 1, которое называется условием максимума диэлектрических потерь или характерным временем релаксации, численные значения диэлектрической проницаемости и диэлектрических потерь на одну декаду опаздывают по частотам (см. табл. 3 и 4), то есть все расхождения связаны с выбранной нами моделью раствора с молекулярно-кинетической точки зрения. Видимо, если бы выбор нами модели раствора, то есть выражения времена релаксации совпадал с работой [19], то это расхождение было бы не очень существенным.

Заключение

Следовательно, результаты численных расчетов при выбранной нами модели раствора, потенциал межмолекулярного взаимодействия Ф _аь (т, 0, ф) и радиальная функция распределения д „_ь (т, 0, ф) дали относительно удовлетворительное согласие теоретических и экспериментальных значений и для водного раствора LiI в широком интервале изменения параметров состояния. Частотная дисперсия и в широком диапазоне частот обусловлена наличием диэлектрической релаксации в водном растворе LiI, что является следствием вкладов молекулярных релаксационных процессов. В общем случае область частотной дисперсии коэффициентов e 1 (v) и e ₂ (v) в зависимости от термодинамических параметров состояния составляет 10 2 Гц, что совпадает с результатами общей релаксационной теории и экспериментальными данными [8].