Исследование динамической нагруженности привода водометных движителей амфибийных гусеничных машин

К ПВД АГМ предъявляются высокие требования по уровню надежности. Это связано с тем, что отказ одного элемента привода исключает возможность движения на воде. В то же время опыт эксплуатации АГМ и результаты экспериментального исследования опытных образцов свидетельствуют об ограниченной долговечности элементов ПВД. До 85 % нарушений функционирования происходят вследствие возбуждения колебательных процессов, что и определяет актуальность проведения исследований, направленных на снижение динамической нагруженности ПВД АГМ.

Методы проектного расчета АГМ основаны на работах А.П. Степанов [1], которые в свою очередь, базируются на теории корабля и приведены в работах Я.И. Войткунского [2]. Водоходные движители были достаточно подробно рассмотрены А.А. Русецким [3], А.Н. Папиром [4], С.В. Куликовым [5]. В этих работах рассмотрена струйная теория водометных движителей и предложены методы определения оптимальных параметров элементов конструкции проектируемых машин. При известных методах проектного расчета номинальные размеры деталей приводов определяются из условия обеспечения прочности и долговечности в зависимости от нагрузок, рассчитываемых с учетом коэффициента динамичности [6] без учета высокочастотных составляющих динамического процесса. Это приводит к ограничению ресурса элементов ПВД. Таким образом, обзор известных методик проектного расчета показал, что оценке особенностей динамического нагружения ПВД не уделяется требуемого внимания.

Кроме того, экспериментальными исследованиями опытных образцов АГМ установлено, что высокий уровень вибронагруженности приводит к ослаблению болтовых соединений крепления опор элементов конструкции привода с последующим их разрушением. Анализ литературных данных показал [7–11], что ослабление болтовых соединений происходит вследствие уменьшения коэффициента трения в резьбовом соединении при высокочастотных вибрациях, что приводит к уменьшению трения в резьбе, а в отдельных случаях – к полной потере самоторможения [12]. Поэтому в работе выдвигается гипотеза о том, что одной из причин ограничения долговечности является ослабление болтовых соединений [13]. На практике болтовое соединение всегда требует достаточно большого предварительного натяга, гарантирующего передачу усилия между соединяемыми элементами. Тем не менее из-за работы в тяжелых условиях у болтовых соединений часто наблюдается самоослабление (постепенная потеря предварительного натяга) с увеличение срока службы, что может привести к снижению работоспособности конструкции [14]. В 1969 году Юнкер [15] впервые указал, что поперечное или сдвигающее нагружение является наиболее опасным видом приложения нагрузки, приводящим к самоотвинчиванию. Пай и Гесс [16, 17] ввели понятие локализованного скольжения и классифицировали процесс самоот-винчивания. Касей [18], Идзуми [19] и др. исследовали механизм самоослабления как микроскольжение опорной поверхности. Авторы показали, что возникает ослабление, когда поперечная нагрузка достигает значений в диапазоне от 50 % до 60 % критической нагрузки, приводящей к скольжению опорной поверхности. В последнее время циклическая нагрузка при вращении была принята как еще одна из причин самоослабления [20, 21]. В работе [22] обсуждается теория са-моотвинчивания предварительно натянутых болтовых соединений под действием вибрации, даются рекомендации по пректированию болтовых соединений, позволяющие исключить эффект самоотвинчивания.

В связи с этим проблема прогнозирования динамической нагруженности ПВД на этапе проектирования и установления его амплитудно-частотных характеристик, а также исключение возможных последствий по ограничению долговечности в совокупности с особенностями работы болтовых соединений приобретает все большую актуальность.

Одним из эффективных методов решения подобных задач является имитационное моделирование с использованием современных прикладных пакетов программ. Имитационное моделирования при выполнении опытно-конструкторских работ позволяет неоднократно применять модель в однородных численных экспериментах и оптимизировать характеристики проектируемого изделия, существенно сокращая трудозатраты на проведение больших объёмов натурных экспериментов, испытаний и устранений дефектов на стадии создания изделия [23, 24]. Для решения этих задач используются программные пакеты и для моделирования технических объектов и мультидисциплинарных мехатронных систем [25–27].

Теоретическое исследование динамической нагруженности привода водомета АГМ

Расчетная схема системы «двигатель – трансмиссия – водоходный движитель – машина» составлена в соответствии с кинематической схемой. Установлены исходные данные и характеристики структурных составляющих: параметры дизельного двигателя, передаточные числа трансмиссии и угловых редукторов, углы, характеризующие расположение валов карданных передач в пространстве, параметры водометного движителя с учетом присоединенных масс воды и собст- венно АГМ. Имитационная модель системы (рис. 1) выполнена на основе программной платформы LMS Imagine.Lab Amesim.

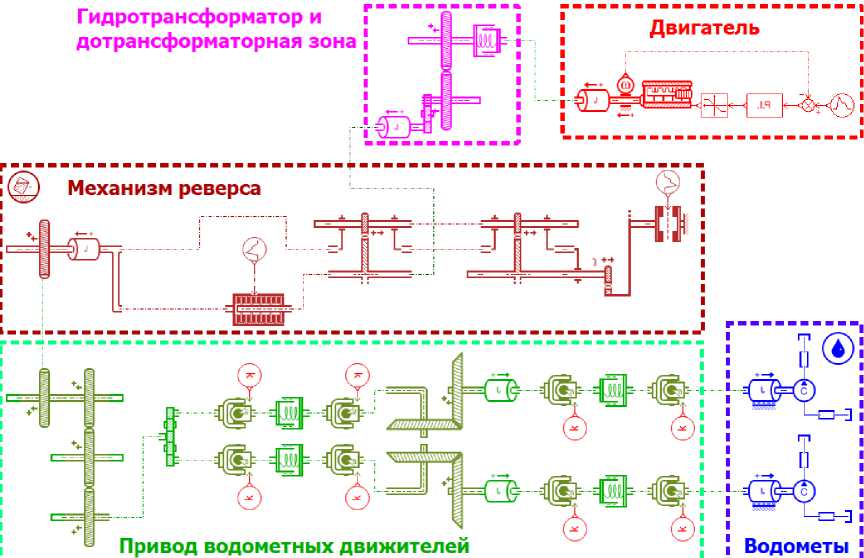
Рис. 1. Имитационная модель привода водометных движителей

Наличие интерактивного графического интерфейса и обширных библиотек компонентов (двигателя, гидротрансформатора, зубчатых и карданных передач и др.) позволяет эффективно проводить имитационное моделирование. Динамическая нагруженность ПВД определялась при следующих переходных процессах: разгон водометов на суше и на воде; вход и выход машины из воды при одновременной работе гусеничного и водометного движителей; включение реверса и др., а также на установившихся режимах движения машины с постоянной скоростью. В качестве примера результатов имитационного моделирования на рис. 2 приведена временная функция динамического момента на валу ПВД при движении задним ходом, выключении механизма реверса и при последующем разгоне амфибийной машины.

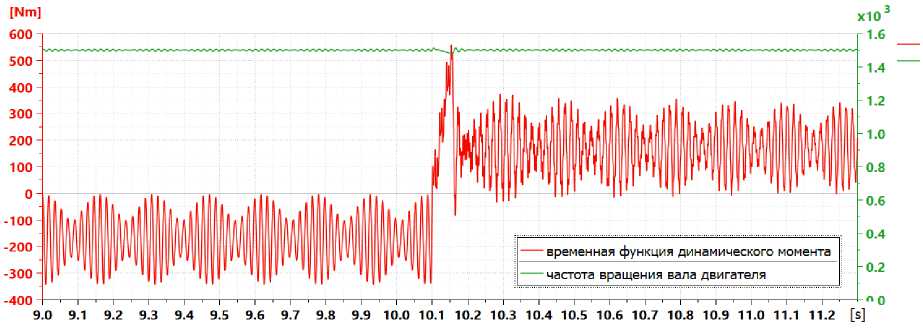
Рис. 2. Временная функция динамического момента на карданных валах ПВД на установившемся режиме и в процессе изменения состояния механизма реверса

Полученные результаты моделирования иллюстрируют возможность возникновения особых форм колебательных процессов в системе (биения на установившихся режимах и свободные ко- лебания на переходных). Кроме режима биения в ПВД происходят также параметрические колебания, формируемые карданными передачами с асимметричными шарнирами Гука, в которых при постоянной угловой скорости ведущей вилки шарнира, соответственно и входного вала углового редуктора дважды за оборот изменяется угловая скорость. Модельная оценка устойчивости на основе анализа качества колебательного процесса по годографу вектора амплитуднофазовой характеристики разомкнутой системы позволяет сделать вывод о существовании неустойчивых периодических режимов.

Анализ результатов имитационного моделирования позволяет утверждать, что одной из главных причин повышенной динамической нагруженности элементов ПВД являются значительные амплитуды ускорений, сопровождающиеся потерей устойчивости колебательных процессов, приводящих к биениям и резонансам, при которых возможно проявление эффекта, описанного И.И. Блехманом, – самопроизвольного ослабления болтовых соединений в нелинейной системе. Для проверки этой гипотезы в программном пакете ANSIS разработана конечноэлементная модель системы «угловой редуктор – опора – корпус» и выполнен анализ напряженно-деформированного состояния. Параметры расчетной модели определены по твердотельным чертежам и 3D-моделям. Условие отсутствия вибрационного ослабления силы затяжки N (отсутствие проскальзывания тела) [7, 8] определяется неравенством

N >  ^, (1) где т - масса углового редуктора и опоры; Аш² - пиковое значение виброускорения; f - коэффициент трения в резьбе при ослаблении.

Расчет показывает, что в рассматриваемой конструкции усилие затяжки составляет N = = 21,38 кН, а требуемая величина должна быть равной 23,37 кН. Таким образом, ослабление болтового соединения вполне вероятно, может привести к колебаниям корпуса редуктора относительно опоры и разрушению привода.

Экспериментальное исследование динамической нагруженности ПВД АГМ

При выполнении имитационного моделирования динамики ПВД принят ряд допущений, корректность которых, а также идентификация отдельных параметров системы выполнялась при экспериментальном исследовании в процессе движения амфибийной машины. Основной целью экспериментального исследования являлось определение силовых и кинематических параметров, характеризующих зависимость динамического момента от частоты вращения вала двигателя. При этом решались следующие задачи :

• 1)    определение амплитудно-частотных характеристик динамических моментов на валах ПВД при движении АГМ на плаву;

• 2)    определение упруго-инерционных параметров элементов ПВД, в том числе рабочих колес водометов с учетом присоединенных масс воды.

Объектом экспериментального исследования является опытный образец АГМ массой 14000 кг, оснащенный дизельным двигателем, четырехступенчатой гидромеханической трансмиссией, ПВД, включающий карданные передачи, угловые редукторы, рабочие колеса водометов, размещенные на днище вдоль бортов изделия.

Для проведения измерений был использован комплекс информационно-измерительной регистрирующей аппаратуры, разработанный на кафедре «Гусеничные машины» КГУ [28]. Управление измерительным комплексом, регистрация и обработка данных производилась с помощью программного обеспечения Power Graph Professional 3.3.9.

В процессе эксперимента определялись следующие параметры:

• 1    – крутящий момент на карданных валах ПВД;

• 2    – частота вращения вала двигателя;

• 3    – виброускорения по трем осям на корпусе углового редуктора.

Экспериментальное исследование выполнялось в соответствии с основными положениями типовой отраслевой методики испытаний на плаву. На установившихся режимах работы частота вращения вала двигателя дискретно изменялась в диапазоне от минимально устойчивых 800 до 2370 об/мин с интервалом 200 об/мин. Фрагмент осциллограммы изменения динамического момента на установившемся режиме и его амплитудно-частотная характеристика приведены на рис. 3.

М.Н*м

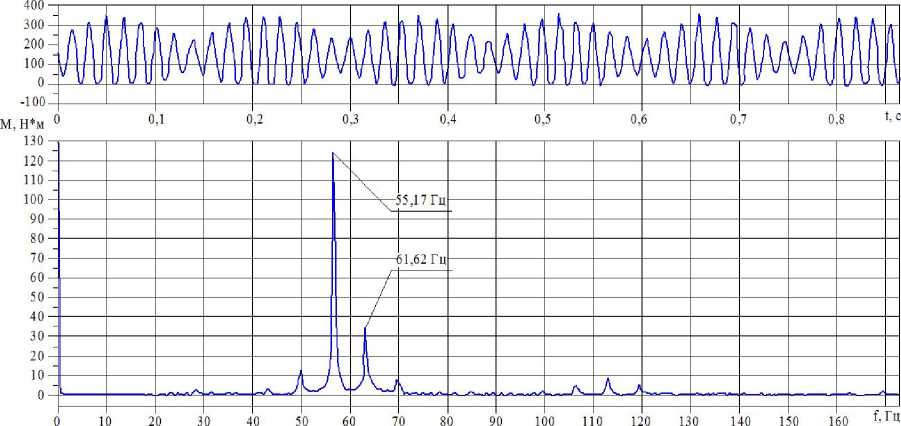
Рис. 3. Фрагмент осциллограммы изменения динамического момента и его амплитудно-частотная характеристика при работе водомета на установившемся режиме

Анализ экспериментальных данных подтверждает результаты моделирования о том, что колебательный процесс носит характер «биений», что вызвано суммированием периодических составляющих момента, близких по частоте. Это определяется величиной передаточного числа углового редуктора (I = ^). В связи с этим частоты периодических составляющих двух карданных валов одного борта на всех скоростных режимах работы двигателя отличаются друг от друга на 11,7 %. Из амплитудно-частотной характеристики динамического момента следует, что максимальная амплитуда момента соответствует «карданной», т. е. двойной частоте вращения приводного вала. Боковые лепестки на амплитудно-частотной характеристике отстоят на ± 6,45 Гц от основного пика и соответствуют частоте биений. Таким образом, действительная амплитуда динамического момента и частота существенно превышают расчетные. При переходном процессе включения – выключения механизма реверса коэффициент динамичности возрастает до 1.9 …3,0.

Экспериментальные значения приведенных моментов инерции определялись при быстром разгоне машины по уравнению: /пр = ^ДД^^р , где ДМ - разность моментов динамического и статического; t _p - время разгона; Дш = Дш д • и пр - скорость вращения водомета, Дш д - скорость вращения вала двигателя, и пр - передаточное ПВД. Приведенный момент инерции водометов с учетом присоединенных масс воды составил /пр = 0,16 ... 0,17 кгм ² .

На рис. 3 приведена зависимость динамического момента в приводе водомета от частоты вращения вала двигателя. График 1 на рис. 3 соответствует расчетной зависимости момента от частоты вращения, определяемой по методике проектного расчета. График 2 характеризует экспериментальную зависимость динамического момента от частоты вращения. Как следует из сопоставления графиков, характер действительной динамической нагруженности ПВД существенно отличается от расчетной, носит циклический характер (колебания на «карданной» частоте и «биения»). Это приводит к возбуждению высокочастотных ускорений, ослабляющих болтовые соединения, накоплению усталостных повреждений и разрушению элементов конструкции ПВД. Установлено, что за 50 часов работы ПВД на оборотах вала двигателя 1500 об/мин число дополнительных, не учитываемых при проектном расчете циклов нагружения при значениях амплитуд и частот динамического момента, существенно превышающих расчетные, составляет более одиннадцати миллионов.

Условие ослабления болтовых соединений приводится ниже.

В соответствии с [29], необходимый момент откручивания болтового соединения рассчитывается по формуле:

Мотв = F^ [tan(^ -^ИГт’тр], Z                          «2

где F - осевое усилие предварительной затяжки, d 2 - средний диаметр резьбы, ^ - угол подъема резьбы (винтовой линии), ф - угол трения, f_T - коэффициент трения на торце резьбы, D_cp - средний диаметр кольца контакта торцов.

Анализ формулы (2) показывает, что главными факторами, оказывающими влияние на усилие, требуемое для откручивания болтового соединения, являются силы трения в витках резьбы и на торце гайки и усилие предварительной затяжки. Оценка отсутствия явления вибропроскальзывания, при котором реализуется эффект самоотвинчивания, выполнена по неравенству (1).

Максимальное значение виброускорения, входящее в неравенство, полученное как расчетным, так и экспериментальным исследованием, принято 271 м/с ² . Полученный результат показал, что условие (1) не выполняется. В связи с этим наблюдается эффект самоотвинчивания. Это приводит к поломке корпуса углового редуктора – крепления проушин к кронштейну. Эффективным способом фиксации резьбового соединения от произвольного самоотвинчивания является применение анаэробного герметика [30, 31]. Применение анаэробного герметика Анакрол 202 позволило увеличить момент отвинчивания на 15 Нм [32] при одинаковом усилии затяжки. Данный факт был подтвержден в ходе экспериментального исследования. После применения анаэробного герметика эффект самоотвинчивания резьбовых соединений креплений угловых редукторов отсутствовал, что обеспечило требуемый ресурс привода водометного движителя.

Заключение

Статистическая обработка результатов расчетно-экспериментального исследования динамики системы свидетельствует об адекватности разработанной имитационной математической модели и эффективности применяемых методик экспериментального исследования.

Результаты выполненных расчетно-экспериментальных исследований позволяют утверждать, что основной причиной ограничения долговечности конструкции ПВД является несовершенство методики проектного расчета, в которой не учитывается динамическая составляющая момента и колебательность процесса нагружения в форме «биений», вынужденных и параметрических.

В связи с этим обоснована необходимость и разработана усовершенствованная методика проектного расчета. По результатам исследования предложены технические решения, обеспечивающие снижение динамического момента, в частности введением в конструкцию гасителя колебаний, позволяющего отстроить резонансные режимы. Эффективным путем исключения параметрических колебаний является сокращение параметра глубины модуляции введением в конструкцию ШРУСов, у которых неравномерность вращения на порядок меньше, чем у асинхронных шарниров.

Для предотвращения разрушения углового редуктора обоснована необходимость повышения жесткости опоры и предложены мероприятия по фиксации болтовых соединений, предотвращающих их самопроизвольное ослабление в условиях повышенной вибронагруженности.

Реализация результатов исследования позволила обеспечить требуемый ресурс привода водометных движителей разрабатываемых амфибийных гусеничных машин.