Исследование динамики нелинейных систем на основе переходных временных рядов
Автор: Кухаренко Б.Г.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика, управление, экономика
Статья в выпуске: 3 (11) т.3, 2011 года.
Бесплатный доступ
Рассматриваются переходные временные ряды для переменных нелинейных динами- ческих систем. На примере численных решений модели Даффинга продемонстриро- ваны особенности спектрального оценивания переходных временных рядов по мето- ду Прони и на основе преобразования Гильберта. Показано, как определяется за- висимость частоты от амплитуды численного решения, представляющего свободное нелинейное колебание. Определение этой зависимости позволяет идентифицировать нелинейную динамическую систему.
Короткий адрес: https://sciup.org/142185765
IDR: 142185765
Текст научной статьи Исследование динамики нелинейных систем на основе переходных временных рядов
-
I. Спектральное оценивание временных рядов для переменных нелинейных динамических систем
-
I.1. Модель локально переходных временных рядов с колебательным изменением и метод Прони
-
Нелинейная система описывается моделью с конечным числом степеней свободы, и в ее пространстве состояний имеется несколько положений равновесия. Если в этом пространстве состояний нелинейная система совершает хаотическое движение, то оно представляется последовательностями локальных орбит возле нескольких ее положений равновесия [1--3]. Причем каждое из локальных движений возле одного из неустойчивых положений равновесия завершается в результате перескока на орбиту возле другого положения равновесия. В результате изменение переменных нелинейной системы во времени имеет гладкий колебательный характер только ограниченное число периодов, после которых с вероятностью единица происходит скачек. То есть если и существует некоторое глобальное колебательное изменение во времени конкретной нелинейной системы, то, как правило, оно представляется только его частичными реализациями. Для нелинейных временных рядов, представляющих хаотическую динамику, естественной является модель локально-переходных временных рядов [4].
Стандартные процедуры локального (во времени) спектрального анализа временного ряда x[1,N o ] (определенного с шагом дискретизации времени At) используют его сегментирование посредством сдвига временного окна фиксированной длины N ^ N o (NAt определяет временной масштаб для локального анализа этого нестационарного в рем енного ряда) [5]. Для локально переходного временного ряда с колебательным изменением x[1,N o ] имеется временной масштаб N At, такой, что в пределах последовательных сегментов
x[n j ,(n j + N — 1)],n j = N • J,J = [0 : round(N o /N )]
огибающая амплитуды колебаний меняется монотонно. Такие сегменты (а значит, и сам ряд локально во времени) характеризуются переходным колебательным изменением.
Если необходимо определить зависимость частоты от амплитуды нелинейных колебаний, то требования к методу спектрального анализа нелинейных временных рядов (представляющих хаотическую динамику) основываются на используемой модели локально переходного колебательного изменения этих временных рядов. То есть сегменты ряда — это не квазистационарные составляющие нестационарного временного ряда (которые для наблюдаемого ряда могли бы оказаться очень малыми по длине), а переходные, то есть с неизменным знаком фактора демпфирования (логарифмического декремента) главных спектральных составляющих сегмента. Использование спектрального анализа, соответствующего модели временного ряда, делает его результаты информативными (то есть имеющими физическую интерпретацию). Поэтому используется метод Прони (Prony R., 1796) [6]. Исторически — это первый метод спектрального анализа временных рядов, но он не имеет непрерывного аналога. Его широкое использование откладывалось из-за отсутствия устойчивого с вычислительной точки зрения алгоритма этого метода. Декомпозиция Прони последовательного сегмента x[1,N] временного ряда x[1,Nq] имеет вид
p
x[i] = X r[l](z[l]) i -1 + n[i],i = 1N
1 =1
где p — число определяемых полюсов сегмента временного ряда;
z[1] = exp(At( —5[1] + j2nf[1])),1 = 1,p — полюса, которые определяются для сегмента временного ряда, где 5[1] и f [1] — соответственно фактор демпфирования (логарифмический декремент) и частота; г[1] = а[1] • exp(j^[1]),1 = 1,р — вычеты в этих полюсах, где а[1] и ^[1] — соответственно амплитуда и фаза; п[1] — аддитивный шум. Длина N последовательного сегмента может быть любой, но лучшие результаты спектрального оценивания получаются, когда размер скользящего временного окна NAt примерно равен двум средним периодам временного ряда x[1,N]. Более плотная выборка значений спектральных параметров временного ряда получается за счет использования дробных сдвигов временного окна.
Создание устойчивого с вычислительной точки зрения алгоритма метода Прони является результатом работ ряда авторов [7--12]. Матричные алгоритмы метода Прони основаны на специальной матричной форме — пучке матриц (matrix pencil) [13]. Для ганкелевой матрицы данных Y размерности (N — L) х (L + 1)
-
Y [1,(N - L) ,I ] = x[I,(I + N — L)] T ,I = 1,(L + 1),
где L — размерность вложения, определяются редуцированные матрицы
-
Y (0) = Y [1,(N — L) ,1L], Y (1) = Y [1,(N — L) ,2,(L + 1)]
и используется свойство понижения ранга пучка матриц
( Y (1) — z Y (0) )
при z = z[1],1 = 1,p. Таким образом, полюса z = z[1],1 = 1,p определяются как обобщенные собственные числа матриц Y (0) и Y (1) . Критерий, позволяющий установить число р главных полюсов сегмента временного ряда, использует разложение сингулярных чисел (SVD):
Y(v) = u(v) • s(v) • (v(v))T,v = [0,1], где
S (v) = diag(s (v ) [1],s (v ) [2],...),s (v) [1] > s (v ) [2] > ... > 0
и
(U(V))TU(v) = I(N-L)X(N-L),(V(V))TV(v) = I(L+1)x(L+1), где I(n-L)x(N-L) и I(l+1)x(l+1) — тождественные матрицы размерности (N — L) х (N — L) и (L + 1) х (L + 1) соответственно, а верхний индекс «T»» обозначает транспонирование [14]. Определяются усеченные матрицы stv) = diag(s(v )[1],...s(v)[p],...,0),v = [0,1].
Использование матриц s t v ) ,v = [0,1] позволяет определить матрицы Y (v ) ,v = [0,1] с фиксированным рангом р. Определение полюсов z i ,l = 1,р как обобщенных собственных чисел матриц
-
Y^) ,v = [0,1] гарантирует вычислительную стабильность определения этих полюсов в пределе временного ряда без шума, поскольку матрицы Y^^v = [0,1] имеют фиксированный ранг р. При минимальном числе полюсов р = 2 аппроксимация по методу Прони последовательных сегментов (гладкого) временного ряда x[1,N g ] позволяет оценить временную зависимость частоты этого временного ряда. Работы по совершенствованию алгоритмов на основе метода Прони для временных рядов, представляющих переменные динамических систем с целью их идентификации, начались в 1990-х и продолжаются до сих пор [15--18].
При определении зависимостей частоты локальных переходных колебаний от их амплитуды для координатно-временных зависимостей моделей с хаотической динамикой методу Прони нет альтернативы. В [4] полученные по методу Прони частичные зависимости частоты временных рядов от их амплитуды (с перекрытием диапазонов изменения амплитуды и частоты) объединяются в полную функциональную зависимость. Результат проверяется в основном (с точки зрения его асимптотических свойств) при малых значениях амплитуды колебаний (малые колебания описываются линеаризованными динамическими моделями, поэтому частоты малых колебаний определяются точно). Это составляет основу для метода выделения в пространстве состояний динамической модели как области переходных последовательностей неустойчивых локальных орбит порядка 1, так и областей устойчивых и неустойчивых глобальных орбит [4]. Однако для более простых динамических моделей переходное колебательное изменение характеризует временной ряд в целом, то есть колебание является непрерывным глобально во времени. В этом случае альтернативой методу Прони при оценке динамических характеристик систем на основе временных рядов является преобразование Гильберта [19]. Это позволяет сравнить результаты двух методов спектрального оценивания для переходных временных рядов с колебательным изменением.
-
I.2. Спектральное оценивание переходных временных рядов с колебательным изменением на основе преобразования Гильберта
Преобразование Гильберта функции x = x(t) имеет вид
∞
(t)=п
х(т)dT t - τ
-∞ и представляет собой фильтр, который сдвигает фазы всех частотных составляющих x(t) на —п/2. Преобразование Гильберта позволяет ввести медленно меняющиеся функции, называемые огибающей a = a(t) и фазой у = ^(t), по формуле
x(t) + jx(t) = a(t)exp(j^(t)).
Таким образом,
a(t) = V (x(t)) 2 + ( e (t)) 2
и
^(t) = arctg( e (t)/x(t)).
Формула для мгновенной угловой частоты имеет вид
w(t) = d^(t)/dt =
x(t)(dx(t)/dt) — (dx(t)/dt)x(t)
Преобразование Гильберта координатно-временной зависимости x = x(t) динамической системы позволяет определить модальные параметры этой динамической системы. Например, в случае квазилинейной динамической системы d2x \dx x d/2 + 25(a) dt + шо(а)х = 0
формулы для временных зависимостей ее модальных параметров имеют вид
^•= “ 2 (t) — "t
(da/dt)2
+ (a(t)) 2
—
(da/dt)(dw/dt) a(t)w(t)
и da/dt dω/dt
-
■t — ■ 2,
то есть зависят от производных огибающей и мгновенной частоты. В линейной системе (то есть dw/dt = 0) фактор демпфирования (логарифмический декремент) 6(t) пропорционален логарифму огибающей a(t).
В случае вынужденных колебаний квазилинейной динамической системы формулы для модальных параметров более громоздкие, поскольку зависят от внешнего возбуждения y = y(t). Формулы для модальных параметров различных динамических систем с демпфированием и описание численной реализации метода спектрального оценивания временных рядов на основе преобразования Гильберта приведены в [19]. В качестве примера ниже приводится сравнение результатов спектрального оценивания на основе преобразования Гильберта (по методу [19]) и по методу Прони для (глобально переходных) численных решений для свободных и вынужденных колебаний в модели Даффинга с демпфированием [20].
-
II. Спектральное оценивание численных решений модели Даффинга
-
II.1. Спектральное оценивание численного решения модели Даффинга без внешнего воздействия
-
Модель Даффинга имеет вид dtx + 26<1 + w2x + Yx3 = y(t), где wo = 2nfo — угловая частота свободных колебаний (при y(t) = 0) с малой амплитудой (при условии x ^ 1 колебания описываются линейным уравнением с y = 0), 6 > 0 — демпфирование и y > 0 — параметр нелинейности этой модели. В [19] в качестве примера рассматривается численное решение модели Даффинга при 6 = 2,5 (сильное демпфирование), собственной частоте fo = 15 и y = 2000 (сильная нелинейность), полученное при начальных условиях x(0) = 10 и (d/dt)x(0) = 0 (рис. 1). Такое решение не может быть оценено методами теории возмущений [20]. На рис. 2 показана оценка огибающей амплитуды колебания на рис. 1 посредством преобразования Гильберта. На рис. 3 показана оценка временной зависимости частоты колебания f = f (t) на рис. 1 посредством преобразования Гильберта. Для t Е [0,0,1] эти оценки (рис. 2 и 3) искажены, а для t Е [0,1,0,4] оценка огибающей (рис. 2) оказывается слегка заниженной. На рис. 4 сплошной линией показана оценка огибающей амплитуды a = a(t) колебания на рис. 1 по методу Прони. На рис. 5 показана оценка временной зависимости частоты f = f (t) колебания на рис. 1 по методу Прони. При убывании амплитуды колебания она асимптотически приближается к значению f = 15 (пунктирная линия на рис. 1).
Для оценок временных зависимостей рис. 4 и 5 по методу Прони отсутствует «краевой» эффект для t Е [0,0,1], характерный для оценок таких зависимостей на рис. 2 и 3. Для t Е [0,0,4] оценка огибающей амплитуды a = a(t) (рис. 4) оказывается слегка заниженной. Действительно, в основе метода Прони лежит линейная модель колебания x(t) = aexp(—6 • t) cos(2nf • t + y), где a — амплитуда, ϕ — фаза, δ — фактор демпфирования (логарифмический декремент), f — частота. Для t Е [0,0,4] профиль нелинейного колебания более крутой, чем у синусоиды, поэтому при аппроксимации этого нелинейного колебания единственной косинусоидой (рис. 4) происходит заниженная оценка его амплитуды. При t ~ 0,4 оценка амплитуды колебаний по методу Прони становится практически точной. Интересно, что такой же эффект имеет место при оценке амплитуды свободных колебаний (рис. 1) на основе преобразования Гильберта (рис. 2). В остальном оценки огибающей амплитуды a = a(t) и временной зависимости частоты f = f (t) колебания на рис. 1, полученные посредством преобразования Гильберта и по методу Прони, оказываются подобными. На рис. 6 представлена зависимость частоты от амплитуды f = f (a) колебания на рис. 1, соответствующая временным зависимостям огибающей амплитуды a = a(t) (рис. 4) и частоты f = f(t) (рис. 5), полученным по методу Прони. Обратная зависимость a = a(f) дает скелетную кривую для модели Даффинга с кубической нелинейностью упругой силы [20]. Скелетная кривая свободных колебаний является характерной для определенного типа нелинейности упругой силы, и определение этой зависимости позволяет идентифицировать нелинейную динамическую систему [19].
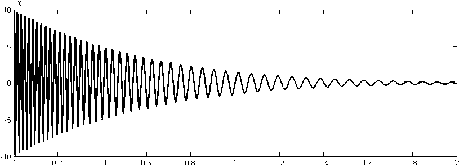
Рис. 1. Координатно-временная зависимость x = x ( t ) для свободного нелинейного колебания
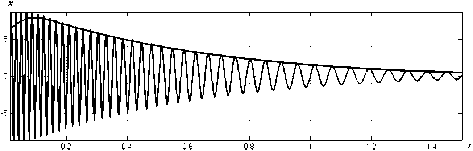
Рис. 2. Оценка огибающей амплитуды колебания на рис. 1 посредством преобразования Гильберта
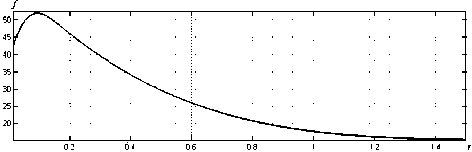
Рис. 3. Оценка временной зависимости частоты колебания на рис. 1 посредством преобразования Гильберта
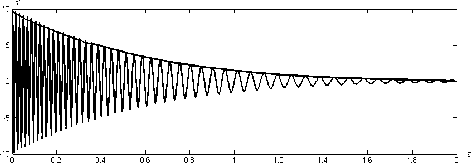
Рис. 4. Оценка огибающей амплитуды колебания на рис. 1 по методу Прони
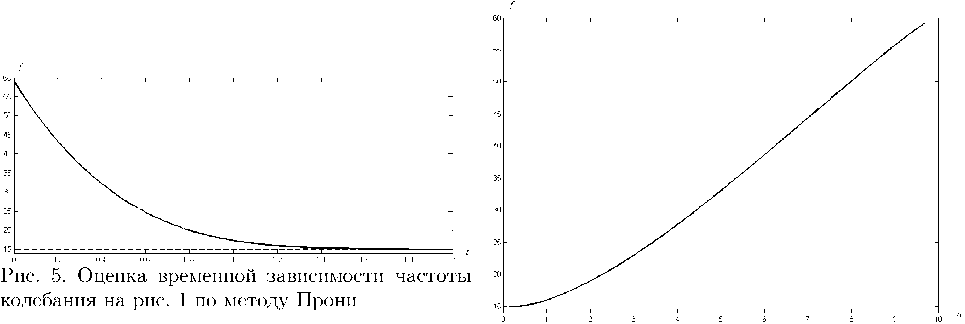
Рис. 6. Оценка зависимости частоты от амплитуды колебания на рис. 1 по методу Прони
-
II.2. Решения модели Даффинга с внешним воздействием
В [19] в качестве примера вынужденного колебания рассматривается численное решение модели Даффинга (рис. 7) при 6 = 2,5 (сильное демпфирование), собственной частоте f o = 30 и Y = 2000 (сильная нелинейность) при начальных условиях x(0) = 0 и (d/dt)x(0) = 0 и синусоидальном возбуждении y = y(t) с линейной зависимостью частоты от времени (рис. 8). При локальном во времени синусоидальном возбуждении y = y ( t ) (рис. 8) вынужденное колебание (рис. 7) также имеет локально синусоидальный характер с переменной частотой. Тем не менее на рис. 9 оценка огибающей амплитуды a = a(t) вынужденного колебания (рис. 7) посредством преобразования Гильберта во временном интервале наступления «резонанса» t Е [1,1,1,3] оказывается заниженной. На рис. 10 показаны оценки временной зависимости частоты f = f (t)
(пунктирная линия) и фазы у = ^(t) (точечная линия) для колебания на рис. 7 и частоты возбуждения на рис. 8 (сплошная линия) посредством преобразования Гильберта, которые отражают «резонансное» поведение решения модели Даффинга при линейном возрастании частоты возбуждения. Однако оценки на рис. 11 и на рис. 12 огибающей амплитуды a = a(t) и частоты f = f (t) вынужденного колебания (рис. 7) по методу Прони являются более точными, чем оценки на рис. 9 и 10 соответственно (отсутствуют эффекты сглаживания, характерные для оценок аналитических методов). Таким образом, и для глобально переходных нелинейных временных рядов спектральное оценивание по методу Прони оказывается наиболее точным.
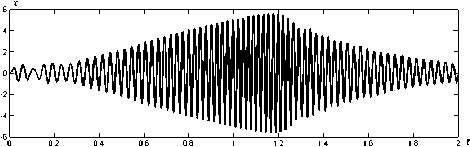
Рис. 7. Координатно-временная зависимость x = x ( t ) для вынужденного колебания
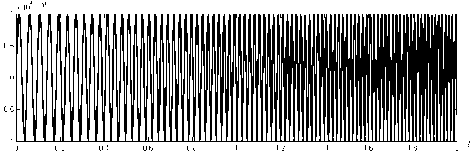
Рис. 8. Временная зависимость y = y(t) для возбуждения
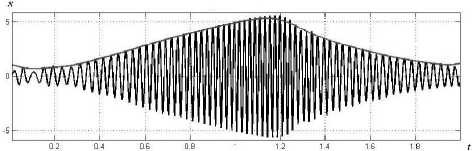
Рис. 9. Оценка огибающей амплитуды колебания на рис. 7 посредством преобразования Гильберта
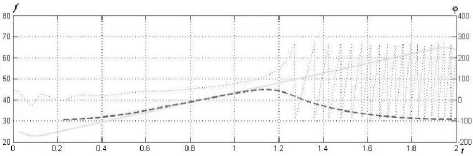
Рис. 10. Оценка временной зависимости частоты колебания на рис. 7 (пунктирная линия) и частоты возбуждения на рис. 8 (сплошная линия) посредством преобразования Гильберта
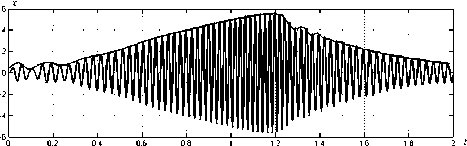
Рис. 11. Оценка огибающей амплитуды колебания на рис. 7 по методу Прони
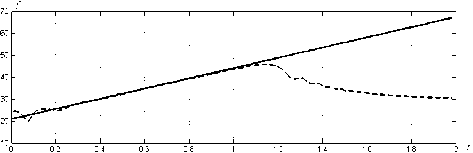
Рис. 12. Оценка временной зависимости частоты колебания на рис. 7 (пунктирная линия) и частоты возбуждения на рис. 8 (сплошная линия) по методу Прони
Список литературы Исследование динамики нелинейных систем на основе переходных временных рядов
- Lichtenberg A.J., Liberman A.P. Regular and stochastic motion/Applied Mathematical Science. -V. 38. -New York, Heidelberg, Berlin: Springer-Verlag, 1983.
- Universality of Chaos: 2nd edition/Ed. by Cvitanovic P. -Copenhagen, Denmark: Niels Bohr Institute, 1989.
- Cvitanovic P., Garpard P., Schreiber T. Investigating of the Lorenz gas in term of periodic orbits//Chaos: An Interdisciplinary Journal of Nonlinear Science. -1992. -V. 2, I. 1. -P. 85-90.
- Кухаренко Б.Г. Исследование по методу Прони динамики систем на основе временных рядов. Труды МФТИ. -2009. -Т. 1, № 2. -С. 176-192.
- Kay S.M., Marple S.L. Spectrum analysis -A modern perspective//Proceedings of the IEEE. -1981. -V. 69, N 11. -P. 1380-1419.
- Prony R. Essai experimental et analytique//Journal de lEcole Polytechnique. -Paris, 1796. -V. 1, I. 2. -P. 24-76.
- Pisarenko V.F. On the estimation of spectra by means of nonlinear function of covariance matrix//Geophysics Journal of Royal Astronomical Society. -1970. -V. 28. -P. 511-531.
- Pisarenko V.F. The retrieval of harmonics from a covariance function//Geophysics Journal of Royal Astronomical. Society. -1973. -V. 33. -P. 347-366.
- Kumaresan R., Tufts D.W. Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise//IEEE Transactions on Acoustics, Speech, and Signal Processing. -1982. -V. ASSP-30, N 4. -P. 833-840.
- Tufts D.W., Kumaresan R. Singular value decomposition and improved frequency estimation using linear prediction//IEEE Transactions on Acoustics, Speech, and Signal Processing. -1982. -V. ASSP-30, N 4. -P. 671-675.
- Hua Y., Sarkar T.K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise//IEEE Transactions on Acoustics, Speech, and Signal Processing. -1990. -V. ASSP-38, N 5. -P. 814-824.
- Hua Y., Sarkar T.K. On SVD for estimating generalized eigenvalues of singular matrix pencil in noise//IEEE Transactions on Acoustics, Speech, and Signal Processing. -1991. -V. ASSP-39, N 4. -P. 892-900.
- Гантмахер Ф.Р. Теория матриц. -М.: Наука, 1966.
- Scharf L.L. The SVD and reduced rank signal processing//Signal processing. -1991. -V. 25, N 2. -P. 113-134.
- Barone P., Massaro E., Polichetti A. The segmented Prony method for the analysis of nonstationary time-series//Astronomy and Astrophysics. -1989. -V. 209, N 1-2. -P. 435-444.
- Sarkar T.K., Pereira O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials//IEEE Antenna and Propagation Magazine. -1995. -V. 37, N 1. -P. 48-55.
- Kukharenko B.G. Use of the Prony method for modal identification of slow-evolutionary linear structures//Journal of Structural Control. -2000. -V. 7, N 2. -P. 203-218.
- Кухаренко Б.Г. Технология спектрального анализа на основе быстрого преобразования Прони//Информационные технологии. -2008. -№ 4. -С. 38-42.
- Feldman M. Hilbert Transform Applications in Mechanical Vibration. -Wiley, 2011.
- Rand R.H. Lecture Notes on Nonlinear Vibrations. -Cornell University, Ithaca, NY: Dept. Theoretical & Applied Mechanics, 2005.


