Исследование динамики шпиндельных узлов станков на основе математического моделирования

Разработка методов расчета и оценки влияния конструктивно-технологических параметров на динамические характеристики шпиндельных узлов (ШУ) является актуальной проблемой при обеспечении качественных показателей функционирования станков. Существенным этапом при изучении этих явлений является математическое моделирование, позволяющее выявить и численно оценить наиболее важные факторы, влияющие на работоспособность шпиндельных узлов станков при эксплуатации и совершенствовании их конструкций.

Исследования проводились в соответствии со структурной схемой (рис. 1). Построение математической модели шпиндельного узла основано на принципе составной модели [1], учитывающей совместно приводной электродвигатель, передаточный механизм, шпиндельный вал, его опоры и режущий инструмент.

В качестве примера на рис. 2 представлена расчетная схема ШУ для процесса плоского шлифования периферией круга. Электродвигатель замещается эквивалентной массой, а механическая характеристика двигателя представляется в форме зависимости движущего момента от угловой скорости ротора ω: M _д= / (го). Связь вала шпинделя с двигателем,

осуществляемая передаточным механизмом, замещается упругим элементом, характеризуемым приведенным коэффициентом жесткости C ₃. В качестве передаточных механизмов могут применяться зубчатые, ременные и другие типы передач. Система двигатель - передаточный механизм имитируется блоком 1 . В качестве примера опор шпиндельного узла приняты подшипники качения. Они представляются в виде эквивалентных упруго-демпфи-рующих связей (рис. 2).

В качестве примера на рис. 2 представлена расчетная схема ШУ для процесса плоского шлифования периферией круга. Электродвигатель замещается эквивалентной массой, а механическая характеристика двигателя представляется в форме зависимости движущего момента от угловой скорости ротора ω: M _д= / (го). Связь вала шпинделя с двигателем, осуществляемая передаточным механизмом, замещается упругим элементом, характеризуемым приведенным коэффициентом жесткости C ₃. В качестве передаточных механизмов могут применяться зубчатые, ременные и другие типы передач. Система двигатель - передаточный механизм имитируется блоком 1 . В качестве примера опор шпиндельного узла приняты подшипники качения. Они представляются в виде эквивалентных упруго-демпфирующих связей (рис. 2).

На рис. 2 обозначены: C x , C z - коэффициенты жесткости опор в вертикальной и поперечной плоскостях; h демпф x , h демпф z - коэффициенты сопротивления; h x , h_z - функции погрешностей колец подшипников в тех же плоскостях.

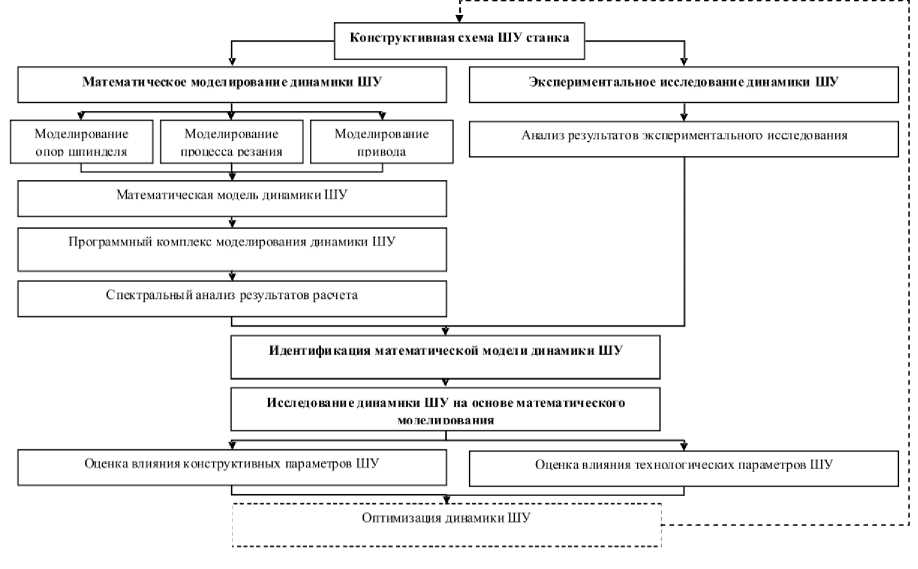
Рис. 1. Структурная схема исследований

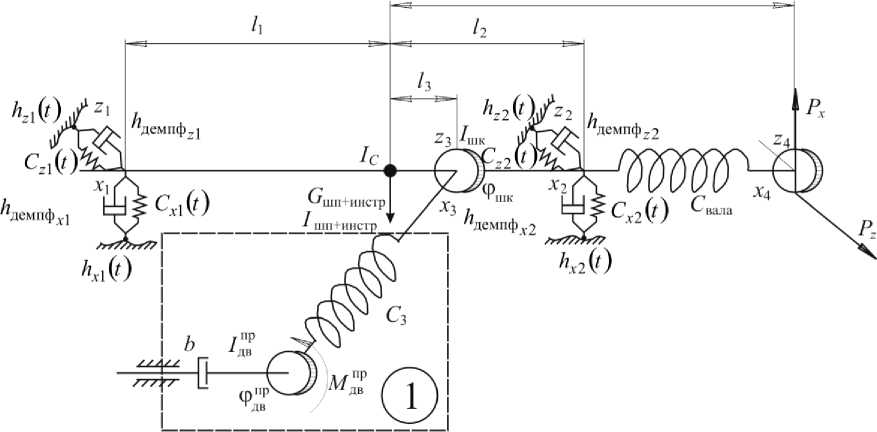
Рис. 2. Расчетная схема шпиндельного узла

Упругие характеристики опор качения обладают нелинейностью и параметричностью (рис. 3), так как их изменение при вращении обусловлено изменением расположения тел качения относительно линии действия радиальной составляющей нагрузки, и зависит от числа тел качения, нагрузки и зазора.

Рассматривается случай, когда учитывается только крутильная жесткость вала шпинделя. Введены следующие параметры: C _вала — приведенная крутильная жесткость шпинделя; I c , I пр и I _шп+ ин _стр — момент инерции вала шпинделя, приведенные моменты инерции ротора двигателя и системы шпиндель-инструмент;

M пр - приведенный движущий момент, развиваемый на валу электродвигателя.

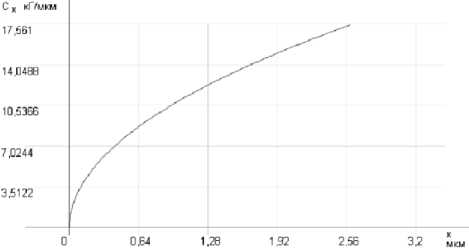
а) зависимость от перемещения внутреннего кольца подшипника

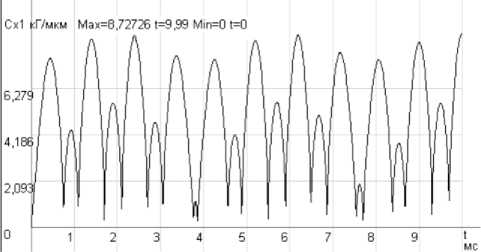
б) зависимость от времени

Рис. 3. Диаграммы изменения коэффициента жесткости опор качения в вертикальной плоскости

На динамику шпиндельного узла существенное влияние оказывают внешние факторы, к которым в первую очередь следует отнести силу резания, возникающую в процессе обработки детали. Для случая плоского шлифования силы резания представляются аналитическими зависимостями, позволяющими в явной форме учесть основные параметры процесса резания в виде (1). При этом введены коэффициенты характеризующие параметры материалов обрабатываемой детали и абразивного инструмента, а также режимы шлифования [2]:

(            К            х 1 + V

0,185 • U • Kb • d     n Ц/|

P = L--------K-----------1ST'' V )x x                               V              Д

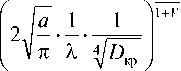
4 n + V + 6

xt

n + 0,5

• V T'f ^{1 +} — 1 ' * V • tg fa + r )

L T 1

где P x и P z – соответственно радиальная и тангенциальная составляющие силы резания (рис. 2).

Внешние (по отношению к шпиндельному узлу) динамические возмущения, передаваемые через несущую систему станка, в математической модели представляются разложением в ряд Фурье. С учетом перечисленных выше особенностей, математическая модель динамики шпиндельного узла в вертикальнопоперечной плоскости имеет вид:

[^]- И+ [B(^,t)l[r]+ [c]• [f] + [F(Y,t)] = [Q(Y,t)], где: [A] – матрица постоянных инерционных коэффициентов; [B] – матрица коэффициентов демпфирования; [C] – матрица коэффициентов жесткостей системы; [F] – вектор- столбец параметрических и нелинейных составляющих коэффициентов жесткостей правой и левой опоры шпинделя; [Q] – вектор-столбец обобщенных сил. Следует отметить, что вектор [Q] формируется с учетом заданной схемы резания (подвод инструмента, врезание и т. д.).

В качестве обобщенных координат приняты следующие параметры (рис. 2): x1, x2 и z1, z2 – соответственно вертикальные и поперечные перемещения шпинделя в правом и левом подшипниках; x3, x4 и z3, z4 – вертикальные и поперечные перемещение шкива шпинделя и пр инструмента; рдВ , фшк и финстр - угловые перемещения ротора двигателя, шкива шпинделя и инструмента.

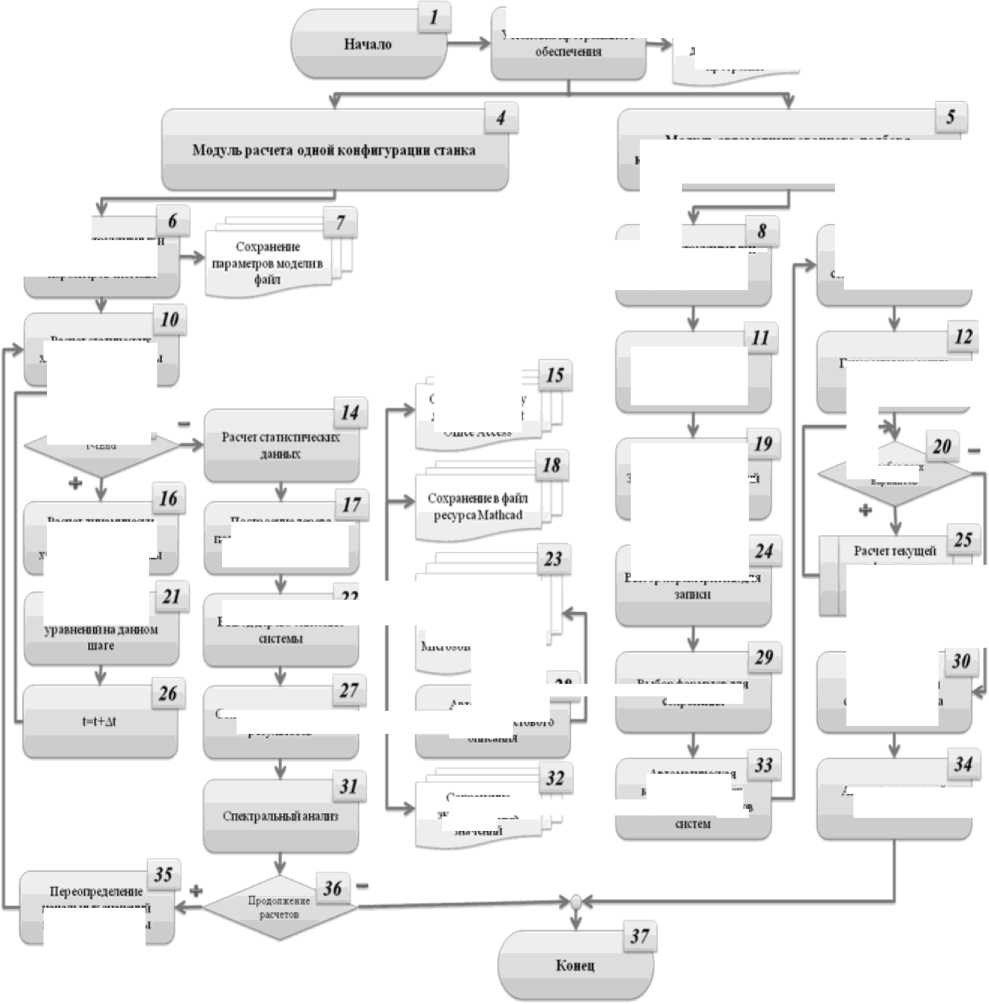
Особенность модели (2) в том, что кроме вертикальных и поперечных колебаний учитываются крутильные колебания сечений шпинделя, поскольку это влияет на поведение инструмента. Математическая модель является параметрической и нелинейной из-за периодических изменений и нелинейности коэффициентов жесткостей и демпфирования опор качения. Расчет динамических характеристик системы (2) реализуется в виде программного комплекса SpindelDinamic 6.6020 [3] на базе IBM PC средствами языка программирования C # в среде Visual Studio.NET. В основу решения положен метод Рунге-Кутта с автоматическим выбором шага. Принципиальный алгоритм программного комплекса представлен на рис. 4. Программный комплекс содержит два основных модуля:

• 1)    расчет и прогнозирование виброхарактеристик существующих шпиндельных узлов (рис. 4, блок 4);

• 2)    подбор режимов резания и проектирование элементов конструкции шпиндельного узла (рис. 4, блок 5).

Решение задач первого модуля состоит из трех частей: задание параметров модели, расчет, вывод и анализ результатов моделирования, а именно: виброперемещений, виброскоростей, виброускорений, спектров собственных частот характерных точек шпинделя и инструмента, и силовых характеристики опор.

Расчет модели условно можно разделить на две задачи: расчет статических параметров системы (рис. 4, блок 10); расчет динамически изменяющихся параметров (рис. 4, блок 16) и решение системы уравнений (рис. 4, блоки 13, 21, 26). После решения системы дифференциальных уравнений производятся: обработка результатов (рис. 4, блок 14), спектральный анализ (рис. 4, блок 31), составляется текстовое и графическое описание системы (рис. 4, блоки 17, 22).

Установка программного

Изучение документации по программе

Сохранение экстремальных тначенй

Выбор форматов для сохранения

Выбор католога для сохраненнярезультатев

Анализ полученной ннформатп!

начальных «начета oi параметров системы

Рис. 4. Принципиальный алгоритм программного комплекса SpindelDinamic 6.6020

Модуль явтомат1«ровя1вого подоора конструктивных и технологических параметров

технолоппеских пар а метров системы

Вводконструкпвныхн ' технологических параметров системы

Расчет стапгтешк характеристик системы

Выбор варыууемых параметров

Генчэацня иерархии папок

Сохранение» базу данных Microsoft Office Access

Заданиенабора значеяй

Перебор всех вариантов

Расчет динамически вменяющихся характеристик системы

Построениедерева пользовательских таблиц и графиков

Решение системы

Выводдатева описания

Сохранение поле ченных резхлыатов

Выбор характериспосдпя

Сохранение текстового описания системы в файл Mier080# Office Word

конфигурации!! сохранение результатов

Автоматическое состакпенне текстового описания

Автомаппеская конфшу рация всех допусп!мых вариантов

Очистка памяти и составление отчета

Предусмотрен расчет модели на отдельных временных интервалах процесса обработки (рис. 4, блоки 35, 36). Алгоритм реализации задач второго модуля по автоматизированному подбору конструктивных и технологических параметров заключается в том, что на первом этапе вводятся параметры системы (рис. 4, блоки 8, 11, 19). После этого формируется план численного эксперимента и составляется иерархия папок (рис. 4, блоки 12, 33). Расчет всех комбинаций проводится по алгоритму, представленному выше (рис. 4, блок 4) с анализом полученной информации (рис. 4, блок 34). Моделирование влияния конструктивно-технологических факторов процесса плоского шлифования периферией круга на виброактивность ШУ осуществлялось на примере станка 3В642. На рис. 5 представлен фрагмент одной из расчетных осциллограмм.

Для подтверждения правомерности предложенной модели (2) проведен натурный эксперимент. Динамические характеристики элементов ШУ в процессе плоского шлифования при различных режимах резания осуществлялось системой вибрационного мониторинга и диагностики роторных машин ОАО ВАСТ («ВиброАккустические Системы и Технологии», Санкт-Петербург). Скорость электродвигателя регулировалась с помощью инвертера SJ 200-015 NFEF / NFU фирмы « Hitachi ». Схема проведения эксперимента представлена рис. 6.

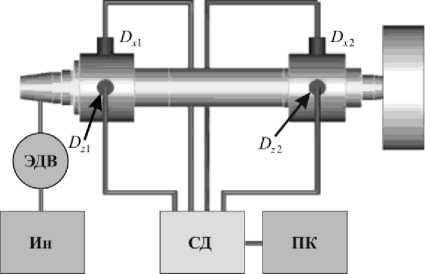
Рис. 6. Схема проведения эксперимента: ЭДВ – электродвигатель; Ин – инвертор SJ 200; D x 1 , D_{x 2} , D_{z 1} , D_{z 2} – пьезоэлектрический датчик; СД – переносной анализатор сигналов - сборщик данных СД-11; ПК – персональный компьютер

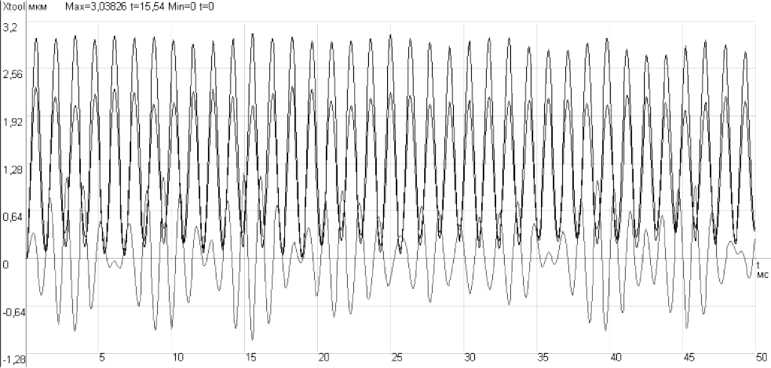
—— - виброперемещения шпинделя в левой опоре

--вибропсремсщсния шпинделя в правой опоре

--виброперемещения инструмента

Рис. 5. Фрагмент графиков виброперемещений шпинделя в опорах в вертикальном направлении

Обрабатывалась деталь из конструкционной стали 12Х2Н4А посредством электроко-рундового шлифовального круга типа 1-250x40x75 24А25НСМ26К5. Частота вращения шпинделя варьировалась с шагом 500 об/мин в диапазоне 500-4500 об/мин. Замеры проводились с помощью микропроцессора прибора СД-11 по 10 линейным усреднениям для каждого опыта, что гарантирует надежность измерений. В каждом замере определялись характеристики общего уровня виброперемещения, виброскорости, виброускорения типа «пик», «пик-пик» и среднеквадратичное отклонение «скз», а также усредненный спектр указанных характеристик. После проведенных измерений отслеживались величины вибрации на выбранной частоте по имеющемуся спектру анализатором СД-11 и на персональном компьютере, после передачи данных со сборщика. Сравнение спектра собственных частот на основе преобразования Фурье при моделировании с результатами экспериментальных замеров автоспектра динамических характеристик показало точность 15%. Фрагменты результатов теоретических и экспериментальных исследований для левой опоры шпинделя в вертикальном направлении представлены рис. 7.

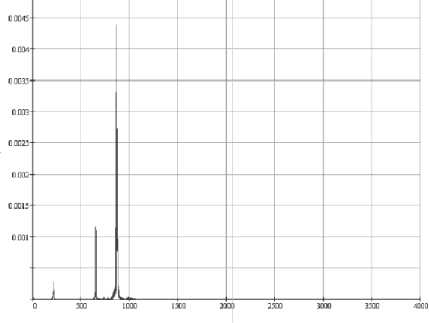
а) спектр собственных частот, полученный при моделировании – 212; 649,5; 833,5 Гц

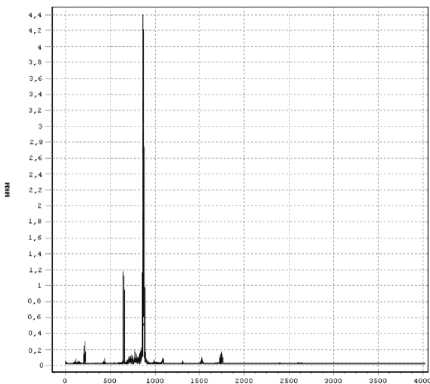
б) спектр собственных частот, полученный из эксперимента – 236; 632; 794 Гц

Рис. 7. Вертикальные колебания шпинделя при частоте вращения 2000 об/мин

Таким образом, появилась возможность направленного исследования влияния конструктивно-технологических параметров на динамку ШУ с помощью математического моделирования на основе соотношений (2). Процедура моделирования заключалась в варьировании определенных конструктивно-технологических параметров и режимов резания при неизменных остальных. Результаты расчетов формировались в виде таблиц и соответствующих им диаграмм. На рис. 8-11 представлены диаграммы виброперемещений элементов ШУ в зависимости от изменения технологических параметров шлифования. Так, например, в проведенных расчетах для опор типа 36208 значения максимальных виброперемещений инструмента в зависимости от изменения технологических параметров в заданных диапазонах (рис. 8-11) представлены в табл. 2.

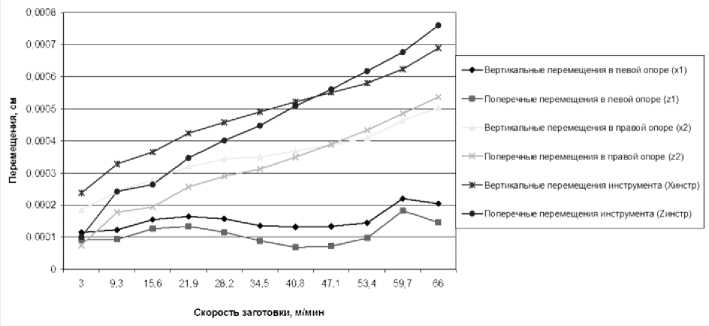
Рис. 8. Зависимость максимальных виброперемещений от скорости заготовки

Поперечные перемещения в правой опоре (z2)

Поперечные перемещения инструмента (2инстр)

Вертикальные перемещения в левой опоре (х1)

Поперечные перемещения в левой опоре (z1)

Вертикальные перемещения инструмента (Хинсгр)

Вертикальные пе ремещения в правой опоре (х2)

Поперечная подача, мм/ход

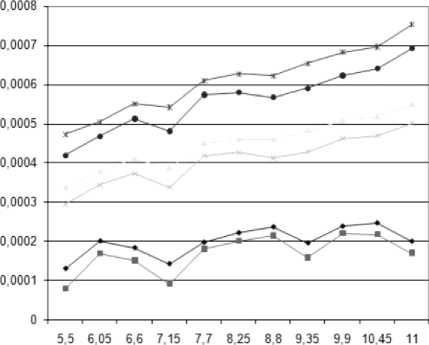
Рис. 9. Зависимость максимальных виброперемещений от поперечной подачи

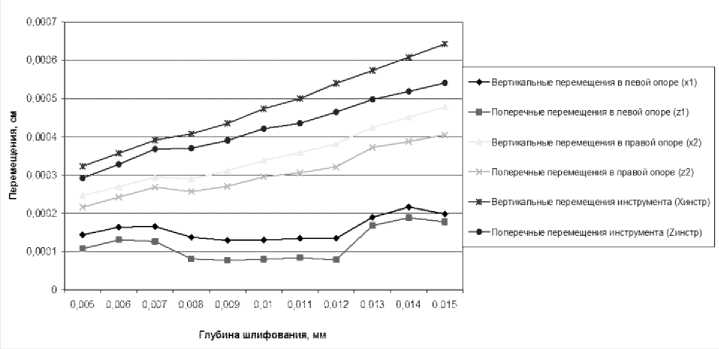
Рис. 10. Зависимость максимальных виброперемещений от глубины шлифования

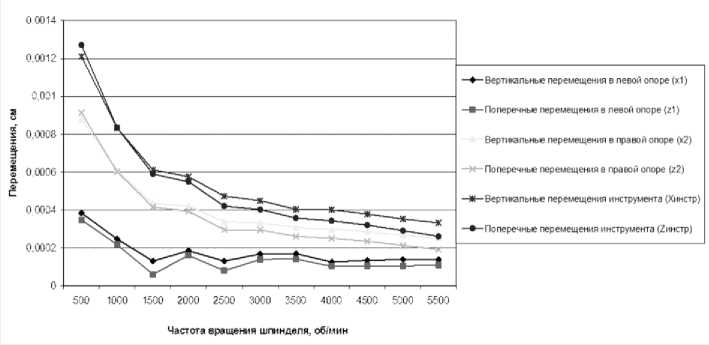
Рис. 11. Зависимость максимальных виброперемещений от частоты вращения шпинделя

Таблица 2. Зависимость максимальных виброперемещений от режимов резания

Изменение технологического параметра	Максимальные виброперемещения, мкм
	вертикальная плоскость	поперечная плоскость
увеличение скорости заготовки	6,9	7,6
увеличение поперечной подачи	7,53	6,93
увеличение глубины шлифования	6,42	5,41
уменьшение частоты вращения шпинделя	12,1	12,71

Аналогично проводилось моделирование динамики ШУ в зависимости от типоразмеров и погрешностей беговых дорожек подшипниковых опор качения при фиксированных режимах обработки. Установлено, что при увеличении количества тел качения подшипников с 10 для серии 66408 до 16 для серии 46108 при n шп =2000 об/мин виброперемещения инструмента уменьшаются в вертикальном направлении с 4,9 мкм до 4,579 мкм; в поперечном – с 4,559 мкм до 4,071 мкм, что составляет, соответственно, 6,5% и 10,7% (рис. 12).

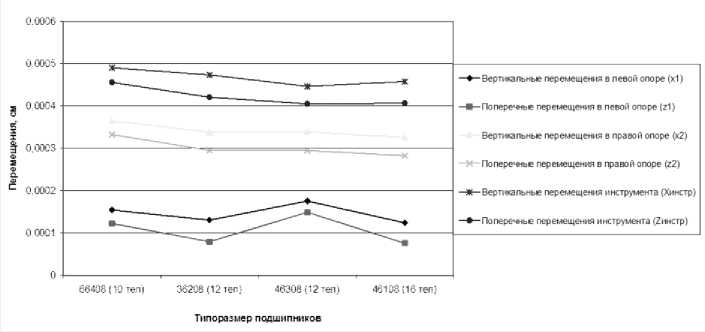
Рис. 12. Диаграммы влияния типоразмера подшипника на виброперемещения инструмента и шпинделя в опорах

При оценке влияния погрешностей изготовления деталей подшипников учитываются погрешности желобов колец. Предполагается недеформируемость тел качения и колец подшипников. Тогда с учетом вертикального и поперечного направлений функции неровностей представляются в виде:

nn hxi

- E A k ^{sin [ k} ( ф с + i Y^{)+ a} k ^{] +} E B k ^{sin [ k (} c Ф с - i Y ) + P k ^] I • cos n i , v k = 1                                   k = 1                                 )

n

n

h zi = I - E A k ^{sin [} k ⁽Ф с ⁺ i Y ) +^a k ] + E B k ^{sin [} k ⁽ c Ф с - i y^{) +} p k ] I • ^sin n _z-

k = 1

k = 1

Численный эксперимент проводился в диапазоне изменения параметров дефектов «волнистости» и «гранности» дорожек качения, установленных из технических условий. По наружным кольцам: высота волнистости А =0,5-3,0 мкм; шаг волнистости Н н =1,5-10 мм; высота гранности В =0,5-2,5 мкм; шаг гранности Н н =6-12 мм. По внутренним кольцам: высота волнистости А =0,5-4,8 мкм; шаг волнистости Н н =1,0-10

мм; высота гранности В =2,0-6,0 мкм; шаг гран-ности Н н =14-24 мм. Фрагменты результатов расчета при учете «волнистости» и «гранности» представлены соответственно на рис. 13, 14. Установлено, что уровень виброперемещений элементов шпиндельного узла при определенных параметрах неровностей значительно превышает допустимый уровень 5 мкм.

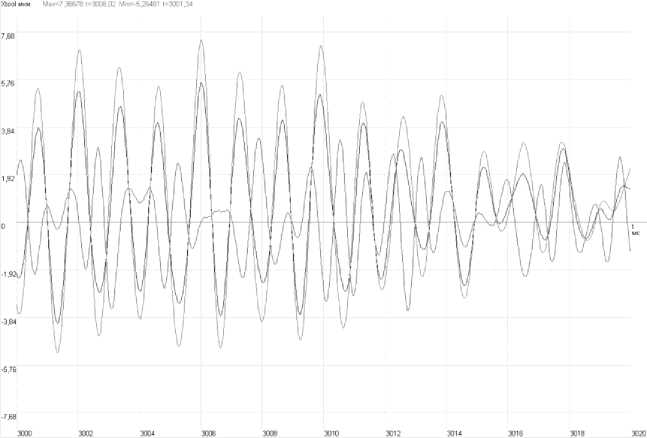
Рис. 13. Фрагмент виброперемещений шпинделя в опорах и инструмента в вертикальном направлении при волнистости дорожек качения: A =1 мкм; H н =1 мм; В =0,8 мкм; H в =10 мм ( n шп =4000 об/мин)

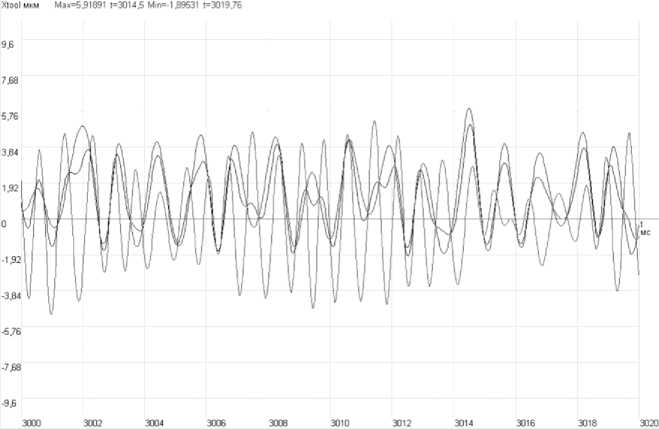
Рис. 14. Фрагмент виброперемещений шпинделя в опорах и инструмента в вертикальном направлении при гранности дорожек качения: A =1 мкм; H _н=10 мм; В =2 мкм; H _в=20 мм ( n _шп=2000 об/мин)

Закономерности влияния конструктивнотехнологических параметров на динамику ШУ при их совместном действии определялись на основе численного факторного эксперимента. За факторы принимаются ранее рассмотренные параметры функционирования ШУ. В качестве целевых функций выбираются: максимальные по модулю значения перемещений, скоростей и ускорений инструмента и шпинделя в левой и правой опорах. Расчеты велись в соответствии с методиками ортогонального центрального композиционного планирования. Из численного двухфакторного анализа совместного учета частоты вращения в диапазоне варьирования от 1000 об/мин до 10000 об/мин, и числа тел качения от 8 до 16 следует, что при заданном режиме резания наиболее существенное влияние на динамику оказывает количество тел качения. Для данного случая геометрическая интерпретация полученных результатов представлена на рис. 15.

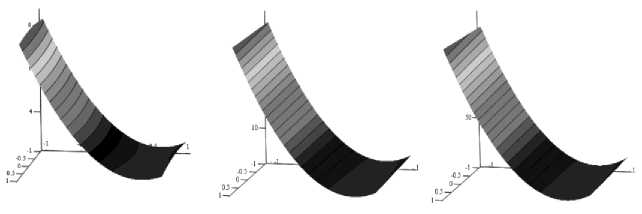
а)                                     б)                                     в)

Рис. 15. Поверхности отклика для максимальных вертикальный перемещений (а), скоростей (б) и ускорений (в) инструмента

Таким же образом проводился численный эксперимент с тремя факторами: поперечной подачей, скоростью заготовки и глубиной шлифования. Из расчетов установлено, что в выбранных диапазонах варьирования все параметры оказывают существенное влияние на динамические характеристики. Геометрический образ целевых функций представлял собой четырехкоординатную гиперповерхность, которая для удобства анализа проецировалась на координатные плоскости.

Вывод: предложенный комплекс по изучению динамики дает возможность эффективно производить количественные и качественные оценки показателей функционирующих и проектируемых шпиндельных узлов металлорежущих станков.