Исследование динамики спроса инновационного товара в контексте теории распространения информации

Производство инновационного товара в настоящее время особенно актуально и в связи с политической обстановкой, и серьезными задачами импортозамещения. К сожалению, этап коммерциализации таких товаров является слабым звеном в инновационном процессе. Ввиду существенных особенностей инновационного товара, обладающего принципиально новыми свойствами для потребителя, имеет место особая динамика спроса. Процесс продаж инновационного товара обладает рядом особенностей. В первый момент поступления инновационного товара на рынок сведениями о нем обладает малая группа потенциальных покупателей. Особое значение принимает время принятия решения о приобретении инновационного товара. В основе динамики спроса находится процесс распространения сведений об инновационном товаре и соответствующие реакции потенциальных покупателей. Рассмотрим работы в контексте теории распространения информации с це лью выявления в них учета особенностей иннова ционного товара при его реализации.

В работе В.В. Цыганова и Ю.Г. Бочкаревой [1] рассматривается общий подход к описанию распространения информации. Приведена условная схема распространения информации (рис. 1). Рекламода тель - лицо, заинтересованное в распространении информации, которое на первом этапе происходит через СМИ. Информацию на первом этапе получает аудитория, затем через межличностные отношения информация распространяется и до других членов общества - адресат.

Рассматривается важность сенсационности сообщения, вводится ее мера. Также приводится математическая модель распространения конкурирующей информации в виде системы дифференциальных уравнений:

dN

—L = Nir dt

n

- Z b j N j , j = 1

Г =P-p( a i — b i) , i = 1, n , (1)

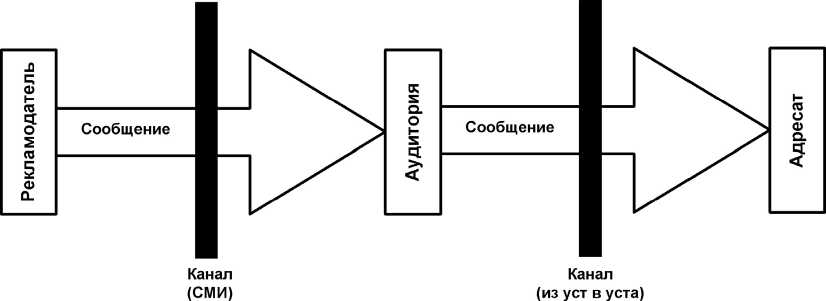
Рис. 1. Структура коммуникационной системы

где р - удельное количество средств коммуникации на душу населения; a_i – доля объектов целевой аудитории, воспринимающих сообщение, как сенсационное; b_i – доля объектов целевой аудитории, не придающих сообщению значения; в - коэффициент согласия. Работа представляет интерес в виду рассмотрения процесса распространения информации с точки зрения сенсационности и представления структуры распространения информации. Однако следует отметить, что процесс распространения информации значительно более сложен. Информации свойственно устаревать, значит, появляются такие категории носителей информации, которые нельзя отнести ни к информирующим, ни к информируемым.

В соответствии с исследованием1, проведенной транснациональной аналитической компанией Nielsen о доверии потребителей к рекламе [2, 3] следует отметить, что доверие потребителей к информации «из уст в уста» всегда значительно выше, чем к другим источникам информации (см. таблицу).

По данным Nielsen, наиболее доверяют всем формам рекламы жители Филиппин и Бразилии (67 %), а также Мексики (66 %), ЮАР (64 %) и Тайваня (63 %), а меньше всего – Дании (28 %), Италии (32 %), Литвы (34 %) и Германии (35 %). На российском же рынке наблюдается снижение уровня доверия потребителей к большинству видов рекламы.

Так, если в 2007 году в ходе аналогичного исследования 61 % респондентов сообщили, что доверяют онлайн отзывам других потребителей, то в апреле 2009 так ответили 55 % опрошенных. Два года назад 60 % говорили, что доверяют сайтам брендов, теперь – 47 %. В 2007 году 49 % опро- шенных выразили доверие такой форме распространению информации о продукте, как спонсорство (фирма спонсирует какое-либо мероприятие, например фирма Reebok – производитель спортивной обуви может быть одним из спонсоров организации футбольного матча), а в 2009 году – 41 %. При этом, как и в целом в мире, в России самое заметное снижение уровня доверия к рекла- ме произошло в традиционных видах рекламы – на телевидении, радио, в печатной прессе.

В работе Е.В. Астафьевой и А.Ф. Терпугова [4] строится математическая модель эффективно- сти воздействия рекламы на продажи с учетом эффекта «надоедания» рекламы d П( t) dt

= ( Р ^- c ) • q ( R ( t ) ) ^-a( t )^- D,

' ^dR ( t ) _ dt

= k 0 •« ( t ) - k ( t ) • R ( t ) ,

где П ( t ) - прибыль фирмы в единицу времени;

p – цена товара; c – затраты на производство единицы товара; q - количество товаров; R ( t ) -эффективность рекламы (измеряется в деньгах); а ( t ) - количество денег, вкладываемых в рекламу; D - непроизводственные затраты; k ( t ) - коэффициент, отражающий «надоедание» рекламы, k 0 = к ( 0 ) . Так первое дифференциальное уравнение описывает прирост прибыли как разницу между выручкой и затратами. Выручка считается как произведение разницы между ценой товара и затратами на его производство на объем продаж в момент времени t , который зависит от эффективности рекламной компании. Затраты считаются как сумма постоянных затрат D и затрат на рекламу а ( t ) . Прирост эффективности рекламы (второе уравнение) имеет денежное выражение и равен разнице между вложениями в рекламу и «забыванием» рекламы в денежном выражении, зависящее также от ее «надоедания» для потребителей. При-

Доверие потребителей рекламе в различных медиа*

1.	Рекомендации других потребителей («молва»)	78 %
2.	Реклама в газетах	63 %
3.	Потребительские блоги	61 %
4.	Сайты брендов	60 %
5.	Телевидение	56 %
6.	Журналы	56 %
7.	Радио	54 %
8.	Спонсорские мероприятия	49 %
9.	Электронная рассылка, на которую подписался сам потребитель	49 %
10.	Реклама перед началом киносеанса	38 %
11.	Контекстная реклама	34 %
12.	Медийная (баннерная) реклама	26 %
13.	Реклама в мобильных телефонах	18 %

* В таблице цифры означают процент людей, которые доверяют тому или иному виду рекламы (например, сайтом брендов доверяют шесть человек из десяти).

веденная модель описывает влияние эффекта «надоедания» рекламы на прибыль фирмы, чем вызывает непосредственный интерес.

Похожая модель влияния рекламы на изменение спроса на товар описывается в работе Т. Калашникова и А. Калашниковой [5]:

dn(t) (a(R(t»-c)2 aM

. dt "  4 b ^{a (} t ) , (3) dR ( t )

—df = k •(«( t)-R (t)), где a(t) - затраты на рекламу; П( t) - доход фирмы П(0) = 0; R (t) - эффективность рекламы R (0) = 0 ; c, b, k - некоторый коэффициент. Правая часть первого уравнения представлена в виде разницы оптимального дохода фирмы и затрат на

■ ⁽ a ^{( R (} t ^{)) -} c ⁾² л р рекламу. Выражение получается,

4b если решить задачу оптимального управления объемом продаж при линейной функции спроса. Смысл второго уравнения аналогичен работе [4].

Следует отметить, что, судя по исследованию Nielsen [2, 3], влияние передачи информации «из уст в уста» на объем продаж во много раз выше других источников распространения информации. В виду этого функциональная зависимость объема продаж значительно более сложная, нежели в моделях работ [4, 5].

В работе М.В. Шептунова [6] строится математическая модель распространения информации с учетом ее старения. В качестве основы модели взята модель распространения слухов о товаре [7]:

Nt ) = a N ( t ) ( N 0 - N ( t ) ) , (4) где N ( t ) - число людей, владеющих информацией; N 0 - потенциал рынка, предполагается N 0 >  0

в момент времени t = 0 ; a - коэффициент, отражающий распространение слухов; t – время. В работе принято, что коэффициент распространения слухов зависит от степени устаревания информации [8]:

2.3 1

a(t) = a0 • e T ,                     (5)

где a0 - ценность информации в момент ее воз- никновения; t – время с момента возникновения информации до определения ее ценности; т -время с момента возникновения информации до момента ее устаревания. С учетом устаревания получается результирующая модель распространения информации:

dN ( t )          -

—у2 = «0 • e т • N(t)(N0 -N(t)). (6)

Работа вызывает непосредственный интерес с точки зрения оценки распространения рекламной информации. Однако следует отметить, что динамика изменения количества людей, обладающих устаревшей информацией, зависит прежде всего от скорости распространения конкурирующих информаций, которые, к сожалению, не включены в приводимую модель.

В работе А.М. Семиглазова, В.А. Семиглазова и К.И. Иванова [9] конструируется математическая модель рекламной компании в виде задачи линейного программирования

m с^ kjXj ^ max, j=1

m

^ UijXj < bi, Xj > 0, i = 1, n, j = 1, m, j=1

где с – цена товара; k_j – коэффициент, отражающий льготу для j -й категории потребителей; x_j – количество потребителей в j -й группе, сделавших покупки; b_i – общие затраты на i -й вид рекламы;

a_ij – затраты на одного покупателя из j -й группы i -й рекламы, которые определяются из данных аналогичной рекламной компании. Предполагается, что, имея параметры приведенной модели, можно определить количество покупателей, отражающих спрос. Работа интересна с точки зрения конструирования моделей линейного программирования в сфере маркетинга. Однако следует отметить, что модель не отражает какой-либо функциональной зависимости количества покупателей от реально действующих факторов, таких как: спрос, задержка принятия решения о покупке, времени распространения информации. Если же приведенную модель считать аппроксимирующей, то сомнителен посыл – количество покупателей в каждой j -й группе должно приводить к оптимальности приведенного функционала. Кроме этого, модель является статической, поэтому ее применение возможно лишь в специфичном случае мгновенного распространения информации.

В работе В. Полякова [10] строится графическая модель соответствия сбыта нового товара от рекламных издержек. В качестве кривой сбыта берется кривая жизненного цикла товара. В статье считается, что от рекламы зависит длительность жизни и величина сбыта товара (рис. 2). На рисунке нижняя кривая отражает жизненный цикл товара без рекламы, а верхняя кривая отражает жизненный цикл товара с учетом влияния рекламы.

В качестве графической модели формирования рекламного бюджета взята S-образная кривая (рис. 3) в соответствии с [11].

На рисунке T min – минимальный уровень эффективности, ниже которого траты на рекламную компанию R min будут слишком малы, чтобы реклама была действенной; T max – максимальный уровень эффективности рекламы, если траты на рекламу будут превышать R max, то эффективность рекламы расти не будет.

В результате автор выстраивает зависимость сбыта товара от рекламного бюджета (рис. 4). На рисунке в скобках указаны этапы жизненного цикла товара: этап 1 – введение нового товара на рынок; 2 – рост; 3 – зрелость; 4 – насыщение; 5 – спад.

Работа представляет интерес с точки зрения установления взаимосвязи между динамикой про-

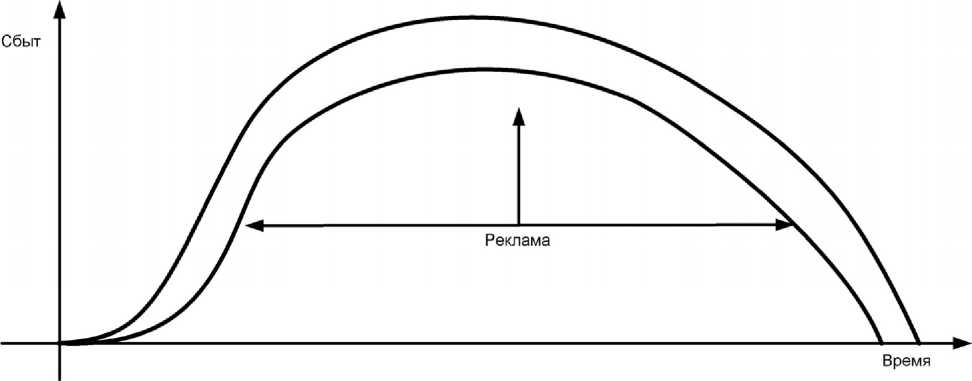
Рис. 2. Графическая модель влияния рекламы на кривую жизненного цикла товара

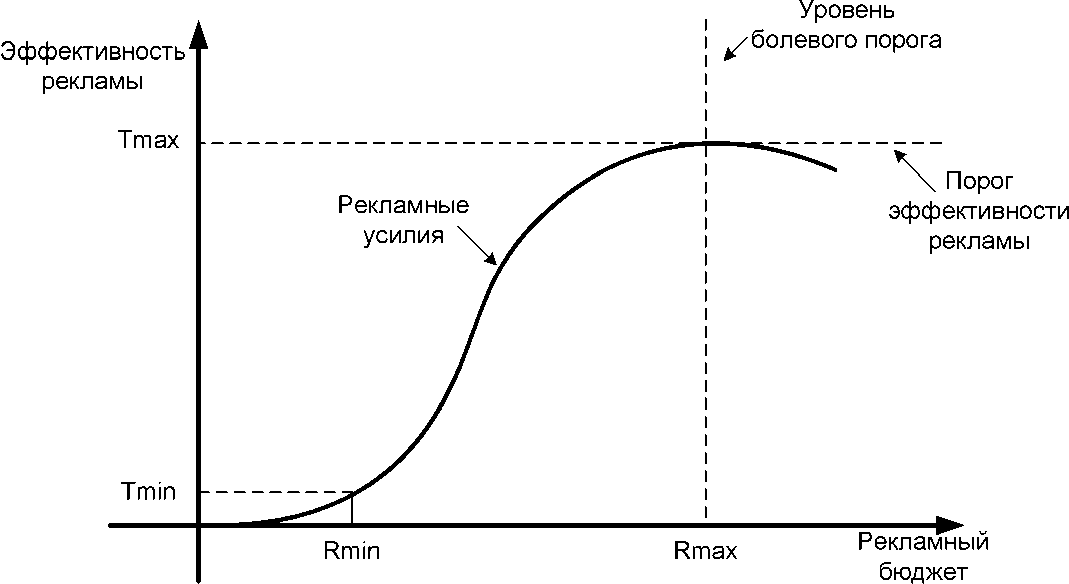
Рис. 3. Зависимость эффективности рекламы от величины рекламного бюджета

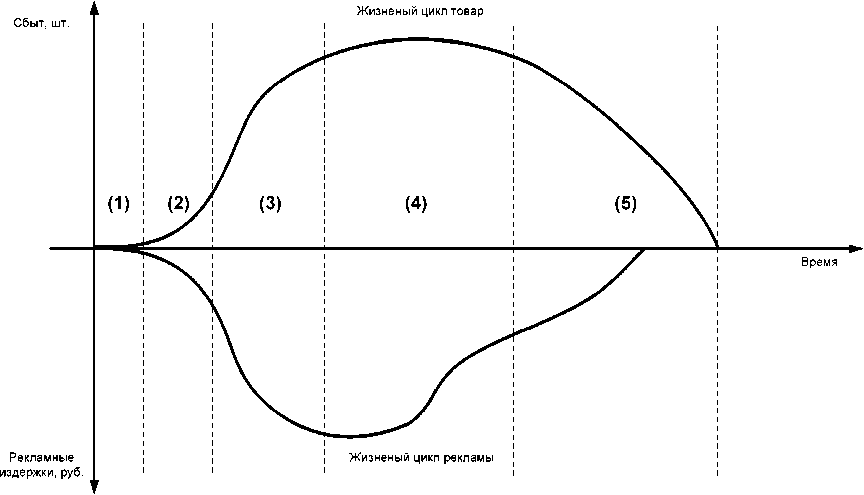
Рис. 4. Графическая модель соответствия этапов жизненного цикла товара и жизненного цикла рекламы

даж инновационного товара и динамикой трат на рекламу. Однако, реклама может влиять лишь на длительность этапов жизненного цикла инновационного товара, а не на суммарную величину сбыта товара, как это предложено в статье (см. рис. 2). Суммарный сбыт зависит в первую очередь от потребностей покупателей и их платежеспособности, а также от многих других внешних факторов. Кроме того, следует также отметить, что, согласно исследованию компании Nielsen о доверии потребителей к рекламе [2, 3], основным источником распространения информации (около 80 % передачи информации) является межличностное общение покупателей. Скорость распространения информации в этом случае зависит не от интенсивности рекламы, а от характеристик самой информации, например, от сенсационности сообщения. Поэтому активная рекламная компания оправдана лишь на начальном этапе жизненного цикла товара, целью ее является информирование «новаторов», которые через межличностные отношения начнут распространять информацию о новом товаре далее по всему рынку.

В статье С.В. Носкова и Е.В. Логиновой [12]

нежную единицу, вложенную в рекламу; λ – коэффициент, отражающий забывание информации. Объем реализации зависит от затрат на рекламу A , текущего этапа жизненного цикла товара M , от характеристик самой информации α и характеристик восприятия потребителей λ .

Следующая модель объема реализации товара учитывает емкость сегмента рынка, долю рынка предприятия, стадию жизненного цикла товара и вид:

Q=

E

1 + a ⋅ e ^{- b ⋅ A}

,

где Q – объем продаж в натуральных единицах;

A – издержки на рекламу; E – емкость рынка; b – доля сегмента рынка предприятия; a – коэффициент, характеризующий эластичность спроса на продукцию предприятия от рекламных расходов в зависимости от стадии жизненного цикла

рассматриваются четыре основные модели зависимости объема сбыта от издержек на рекламу. Модель М. Видаля и Х. Вольфа:

dS M -S =α⋅A dt M

-

λ⋅ S ,

где S – объем реализации товара в момент времени t ; A – объем затрат на рекламу; M – уровень насыщения рынка данным товаром; α – коэффициент, отражающий реакцию сбыта на рекламу, т. е. изменение объема реализации на каждую де-

продукции и вида ее развития.

Далее отмечаются модели принятия решения об издержках на рекламу, основанные на теории игр. Главным преимуществом таких моделей является учет действий конкурентов и выработка на этой основе своих оптимальных действий. Такие модели применимы только при олигополии, когда число конкурентов небольшое и их поведение можно учесть.

Следует отметить, что представленные в работе [12] модели не отражают структуры покупки товара. Так, кроме распространения информации о новом товаре, необходимо учитывать платежеспособность потенциальных покупателей и время, которое требуется человеку для принятия решения о покупке товара. Кроме того, следует отметить,

что распространение информации среди потенциальных покупателей также осложняется устареванием информации, что ведет к распространению «ошибочной» информации о товаре и, следова- тельно, сильно искажает динамику продаж инно- вационного товара.

В работе Л.Л. Делицына и Т.А. Подлесной [13] строится граф распространения информации в социальной сети. Вершинами графа являются люди осведомленные, либо неосведомленные. Осведомление может происходить либо за счет межличностного общения, либо посредством СМИ. Для произвольного графа связей между k индивидуумами требуется решение линейной системы 2k дифференциальный уравнений. Решение такой системы в частном случае соответствует модели

Басса. Полное уравнение для вероятности того, что информированы k индивидов из общего коли- чества популяции K имеет вид:

dx = (a+p-x )(1 - x )-p-Varf—), dt v ’ IK)

где x – доля информированных индивидов, k – количество информированных индивидов, K – объем популяции, a, p - коэффициенты, отражающие влияние рекламы и межличностного общения. При предположении о стремлении к бесконечности количества информированных индивидов и объема популяции уравнение соответствует модели Басса. Результаты работы имеют важное значение, так как связывают инновационный процесс с процессом распространения информации. Однако процесс распространения информации о нововведении более сложен. Обязательно надо учитывать, что информация изменяется во времени, что приводит к изменению поведения индивидов и систе- мы в целом.

В работе Л.Л. Делицына и С.А. Белоцерковской [14] строится модель распространения инноваций в отдельных возрастных группах с учетом процессов воспроизводства населения. Модель представлена в виде системы дифференциальных балансовых уравнений. Построение системы основано на разделении населения на три группы: первая группа состоит из людей, использующих нововведение, вторая группа – из потенциальных покупателей и третья группа – из людей, еще не ставшими потенциальными покупателями. Предполагается, что прирост первых двух групп осуществляется за счет перехода людей из предыдущих групп, убыль из групп также осуществляется за счет смертности населения в этих группах. Факторы перехода людей из групп в группы не рассматриваются, но задаются функциями общего вида. Работа вызывает интерес с точки зрения одного из способов сегментации рынка. Однако следует отметить, что биологические факторы, на основе которых построена модель, имеют второстепенное значение по сравнению с экономическими факто- рами, так как инновационный процесс является значительно более скоротечным по сравнению с жизнью человека, если не рассматривается особенные случаи: война, кризис и т.п. К экономическим факторам, имеющим важное значение, относятся влияние распространения информации о нововведении, спрос на подобное нововведение, задержку приобретения нововведения.

Исследования в области распространения информации проводятся учеными: Malaviya P., Meyers-Levy J. [15], Арговым Н.В., Астафьевой Е.В., Ахмедовой Д.Д., Белоусовым Е.П., Белоцерковской С.А., Бочкаревой Ю.Г., Васильевым Г.В., Видалем М., Вольфом Х., Городецким Д.И., Делицыным Л.Л., Ивановым К.И., Калашниковым Т., Калашниковым А., Логиновым Е.В., Носковым С.В., Подлесным Т.А., Поляковой В., Рымановым А.Ю., Семиглазовым А.М., Семиглазовым В.А., Силаковым А.В., Терпуговым А.Ф., Трухановым М.А., Цыгановым В.В., Шептуновой М.В. и другими.

Как видно из вышеприведенного исследования работ особенности коммерциализации инновационного товара не в полной мере учтены. В этой связи, авторами разработан методический подход и комплекс методов [16–21], программное обеспечение [22] к прогнозированию динамики спроса инновационного товара, учитывающие особенности его формирования. На основе данных разработок построен алгоритм оптимального управления запасами инновационного товара [23]. Основное требование к методическому инструментарию решения задач планирования и управления реализацией инновационного товара свелось к раскрытию механизма формирования его спроса. Этот механизм сводится к поэтапной структуре принятия решения о покупке потенциальными покупателями инновационного товара. В основе этих этапов лежит распространение сведений об инновационном товаре и определенные реакции покупателей по переработке этих сведений. Авторами выделены четыре этапа в рамках рассматриваемого подхода. На первом этапе потенциальный покупатель получает сведения об инновационном товаре либо через СМИ, либо через межличностное общение. На втором этапе потенциальный покупатель оценивает возможность его покупки в зависимости от своей платежеспособности. На третьем этапе потенциальный покупатель принимает решение о покупке товара, которое зависит от его психологического типа и описывается как некоторое запаздывание от момента определения возможности покупки инновационного товара до момента его покупки. На четвертом этапе потенциальный покупатель приобретает инновационный товар.

На основе этапов принятия решения потенциальными покупателями о покупке формируются этапы жизненного цикла инновационного товара, определяющие, в конечном итоге, динамику объема его реализации. Авторами разработан методи- ческий подход к прогнозированию продаж инновационного товара, позволяющий рассчитывать количество покупок к заданному моменту времени, на основе которого разработана модель, включающая следующие показатели: число потенциальных покупателей, получающих сведения о новом товаре в единицу времени; доля потенциальных покупателей, обладающих сведениями о новом товаре и готовым купить его по текущей цене или ниже; доля потенциальных покупателей, которые купят товар через некоторое время после того, как получат сведения о нем. Схема покупок, отражающая основную идею, представлена на рис. 5. По горизонтальной оси откладываются периоды времени (например, недели), начиная с первого момента выпуска инновационного товара на рынок. В каждый период некоторое количество потенциальных покупателей получает сведения об инновационном товаре.

Из этого количества выделяется доля потенциальных покупателей, которые готовы приобрести товар по текущей цене. Однако не все эти потенциальные покупатели в этот же период времени совершат покупку. По вертикальной оси откладывается время (запаздывание) на принятие решения о покупке товара. Так, в период времени, когда потенциальные покупатели получили сведения об инновационном товаре, не все они в тот же период времени совершат покупку. Приобретут товар только М(1,0) количество потенциальных покупателей, во второй период времени совершат покупку инновационного товара, из тех потенциальных покупателей, которые получили сведения о нем в первый период, только М(1,1) количество потенциальных покупателей и т.д. вплоть до заданного периода времени:

M ( T ) = f] ^ ( t ) ■% ( P ) • f ( т ) dtd т , (11) D ( T )

где M ( t ) - количество покупок инновационного товара к заданному моменту времени T ; D(T) -область продаж, заключенная между осями t -время и т - запаздывание и прямой T =T-t ; ^ ( t ) -число потенциальных покупателей, получающих сведения о новом товаре в единицу времени; Х ( P ) - доля потенциальных покупателей, обладающих сведениями о новом товаре и готовым купить его по текущей цене или ниже; f ( т ) - доля потенциальных покупателей, которые купят товар через время т после того, как получат сведения о нем.

Число потенциальных покупателей ^ ( t ), получающих сведения о новом товаре в единицу времени, определяется уравнениями:

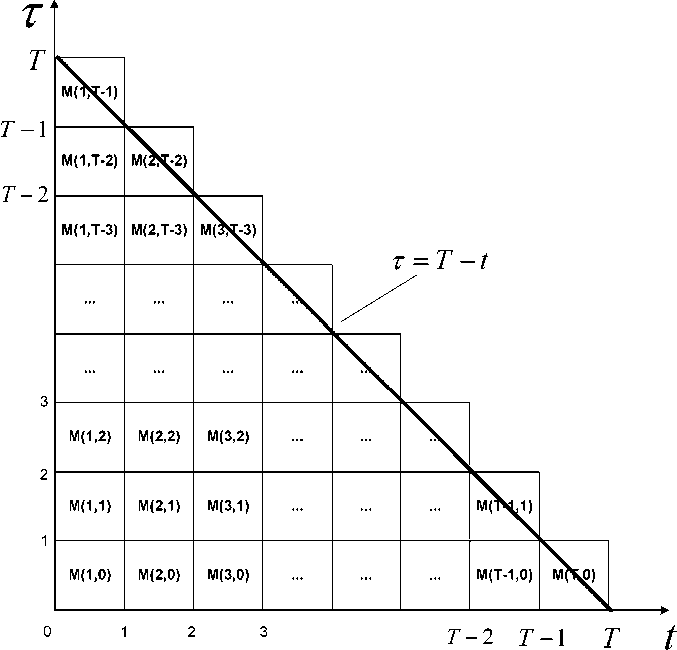
Рис. 5. Схема продаж (в квадратах отмечается количество продаж М ( t , т ) )

^{ф (} t ) = dNj.j.        (t)

dt = (a.5ik,k +p.nik (t))x ik—I x Z N.i2;...;ik-1;j (t)-‘ j=ik-i

- Z ( ^aA , k +P- n j ⁽ t ) ) • ^N_W.. .. ; i k - i ; i k ⁽ t ) ^j = i k ^{+ 1}

. ^N 1 ;i 2 ; ... ; i k - 1 ; i k ⁽ t^{k - 1} ) = °'

( 0 5 m <  m , m - 1 <  m ( 1 <  m <  k ) ) . k

V N .      (t ) = N . U ),

Z-^ i1;i2;.•.;ik-1;j '          i1;i2;.•.;ik-1 k-1/’ j'=ik-1

° < im < m, im-1 < im (1 < m < k - 1)

J Z         i1; i 2;. ■.; ik-1; j i1; ‘2;. ■.; ik-1                                                         .

( ° <  i m <  m , i m - 1 <  i m , ¹ <  m <  k )

Функция x ( P ) покупательского спроса определяется выражением

D ( P ) =Jx ( x ) dx .              (14)

P

Здесь D ( P ) - доля потенциальных покупателей, которые согласны купить товар по цене P и ниже. Обозначение x соответствует P .

Функция f ( т ) отражает долю потенциальных покупателей, которые купят товар через некоторое время т после того, как получат сведения о нем. Есть основания считать, что функция имеет куполообразный вид.

Проверка авторского подхода на реальных данных по продажам инновационного товара подтверждает целесообразность его применения в определении параметров динамики спроса, а значит и в планировании производства инновационного товара.