Исследование динамики управляемого прыжка робота

На данный момент известно достаточно большое число прыгающих роботов, разработанных российскими и зарубежными учеными, отличающихся массой, габаритами, параметрами и технологиями прыжка, способами реализации отрыва от поверхности и приземления на нее [1-5]. Но до сих пор актуальной остается задача проектирования робота, осуществляющего управляемый прыжок с требуемыми значениями высоты и длины, так как практически во всех созданных роботах эти параметры прыжка жестко связаны с характеристиками приводов, посредством которых объекты отрываются от поверхности. Помимо этого в большинстве работ малое внимание уделяется вопросам позиционирования робота после прыжка для реализации последующих.

Описанный в статье робот предназначен для преодоления препятствий при движении по пересеченной местности, высота и длина прыжка которого являются управляемыми параметрами, благодаря разработанной конструкции данный робот может совершать серию прыжков независимо от стороны корпуса, на которую произошло приземление.

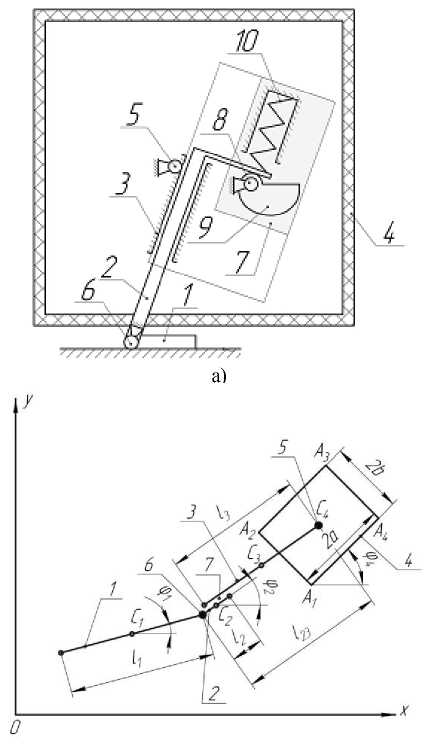
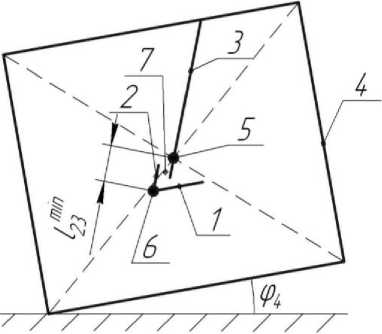
Описание прыгающего робота. В работе предложена следующая конструктивная схема робота, движущегося с отрывом от поверхности (рис. 1, а). Робот состоит из четырех звеньев, представляющих собой стопу – звено 1, ногу – звенья 2 и 3, корпус – звено 4. Звенья 3 и 4, 1 и 2 связаны между собой приводами вращательного движения 5 и 6 соответственно, установленными на звеньях 2 и 4, звенья 2 и 3 – приводом поступательного движения 7, закрепленным на звене 3 и включающим в себя двигатель 8, кулачок 9 и пружину 10. Нога робота установлена в центре симметрии корпуса.

Перейдем к структурной схеме устройства, показанной на рис. 1б. Звенья стопы и ноги будем представлять в виде стержней, а корпус в виде

прямоугольника. Углы φ 1 , φ 2 , φ 4 представляют собой углы между звеньями прыгающего робота и опорной поверхностью, длина ноги определяется величиной l 23 , равной расстоянию между двумя точками, одна из которых является точкой соединения ноги с корпусом, а другая точкой прикрепления стопы к ноге. Будем считать, что робот осуществляет прыжок из начального положения, при котором корпус опирается на поверхность (φ 4 =0⁰), нога полностью втянута в корпус ( l 23 = l 23 ^min), звенья 1, 2 и 3 расположены под некоторыми произвольными углами φ₁ и φ₂.

б)

Рис. 1. Схемы прыгающего робота: а – конструктивная, б – структурная

Задачей рассматриваемого робота является движение по пересеченной местности, высота и длина прыжка объекта определяются его системой навигации исходя из размеров преодолеваемого препятствия. Данная информация обрабатывается системой управления и преобразовывается в угол поворота ноги φ₂⁰, под которым будет осуществляться прыжок, длину ноги l 23 ⁰, на которой будет происходить разгон робота перед отрывом от поверхности, и силу F 23 , создаваемую приводом 7, за счет действия которой происходит прыжок.

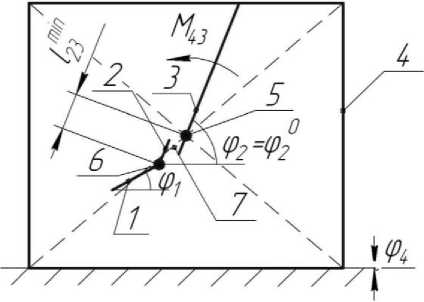
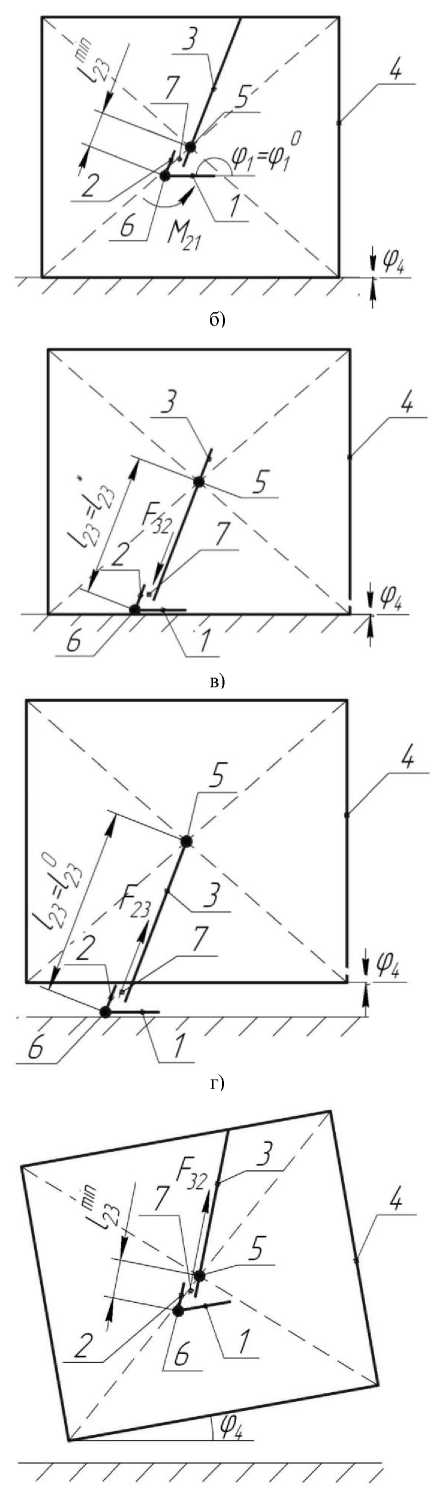
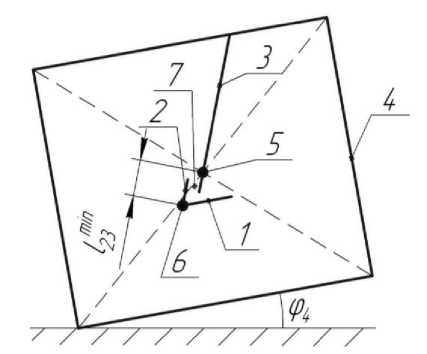
Технология прыжка. Будем рассматривать прыжок устройства состоящим из последовательности этапов, каждый из которых характеризуется определенным видом движения звеньев объекта. Для того, чтобы прыжок робота отвечал требованиям длины и высоты, последний должен позиционироваться, пока его корпус находится на поверхности. Вначале происходит поворот ноги вместе со стопой внутри корпуса при помощи момента М 43 , формируемого приводом 5 до тех пор, пока не будет выполняться условие φ 2 =φ 2 ⁰ (первый этап, рис. 2а). После этого стопа принимает положение, при котором она становится параллельной опорной поверхности, т.е. φ 1 =φ 1 ⁰, под действием момента М 21 , генерируемого приводом 6 (второй этап, рис. 2б). На третьем этапе (рис. 2в) нога со стопой перемещаются внутри корпуса робота за счет относительного движения звеньев 2 и 3 под действием силы F 32 , создаваемой приводом 7, пока стопа не начнет взаимодействовать с поверхностью, длина ноги при этом станет равной l 23 = l 23 ^*. Во время трех описанных этапов объект позиционировался для совершения прыжка, на четвертом этапе устройство разгоняется за счет силы F ₂₃ до достижения скорости, при которой происходит отрыв стопы от поверхности (рис. 2г). Движение с отрывом соответствует пятому этапу (рис. 2д), во время которого также происходит втягивание ноги в корпус при помощи силы F 32 ( l 23 = l 23 ^min). Приземление робота, характеризующееся ударом о поверхность, происходит во время шестого этапа на одну из точек корпуса, после чего на седьмом этапе корпус вместе со всеми звеньями поворачивается относительно точки приземления за счет сил инерции до тех пор, пока одна из сторон корпуса не будет взаимодействовать с опорной поверхностью (рис. 2е).

а)

д)

е)

Рис. 2. а) - первый этап, б) - второй этап, в) - третий этап, г) - четвертый этап, д) - пятый этап, е) -шестой этап

Конструктивной особенностью робота является то, что привод 5 поворота ноги относительно корпуса расположен в центре симметрии последнего, что позволяет устройству совершать следующий прыжок независимо от стороны корпуса, на которую робот приземлится.

Математическая модель прыгающего робота. Для разработки математической модели рассматривается схема рис. 1 б. Движение робота происходит в вертикальной плоскости, с которой связана система координат Оху . Звенья стопы и ноги устройства представляют собой стержни, имеющие длины 1 1 , 1 ₂ и 1 ₃ соответственно, а корпус - прямоугольник А 1 А ₂ А ₃ А ₄ размерами 2 а х2 b. Звенья объекта i =1-4 являются абсолютно твердыми телами, массы m i которых сосредоточены в центрах их симметрии C i . Робот осуществляет прыжок относительно горизонтальной шероховатой поверхности.

Для построения системы дифференциальных уравнений, описывающих движение робота, использованы уравнения Лагранжа второго рода. В качестве обобщенных координат q , j =1-8, выступают проекции q 1 = х 1 , q ₂= y 1 , q ₃= х ₄, q ₄= у ₄ положения центров масс звеньев 1 и 4 на оси Ох и Оу , углы q ₅=ф 1 , q ₆=ф₂ и q ₇=ф₄ поворота звеньев, а также длина q ₈= 1 ₂₃ ноги робота. Кинетическая энергия системы включает в себя кинетические энергии звеньев стопы, ноги и корпуса робота:

т = Е T i=1

•

Каждое звено совершает сложное движение, поэтому кинетическая энергия звена определяется по формуле:

Дифференциальные уравнения движения прыгающего робота в матричной форме имеют вид

Ak (q)q + Bk (q)q + Ck (q)^72123 = Fk(3)

где q - вектор обобщенных координат q = (x1   У1   x4   У4   ^1   Ф2   Ф4   123) .(

Матрицы A ( q ) , B_k ( q ), C_k ( q ) , F_k определяются на каждом из этапов к движения робота в соответствии с разработанной технологией движения.

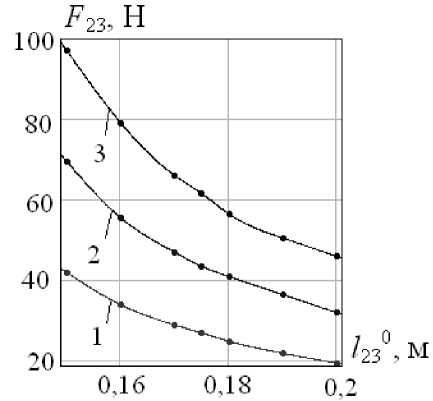
Моделирование движения робота. Целью численного моделирования движения прыгающего робота является выявление зависимостей между параметрами ф₂⁰, 1 ₂₃⁰, F ₂₃, достигаемыми на этапах 1-4, и высотой и длиной прыжка, под которыми понимаются максимальные расстояния, пройденные центром масс корпуса вдоль вертикальной и горизонтальной осей. По графикам рис. 3 и 4 видно, что для реализации прыжка робота на требуемую высоту или длину необходимо варьировать значения двух управляющих параметров: силы F 23 и угла ф₂⁰, силы F ₂₃ и длины ноги 1₂^, длины ноги 1 ₂₃⁰ и угла ф₂⁰. Причем, при постоянной высоте прыжка H значение силы F ₂₃ с ростом угла наклона ноги ф₂⁰ и с увеличением расстояния 1 ₂₃⁰ убывает по криволинейным зависимостям, приведенным на рис. 3, в первом случае кривая близка к экспоненте.

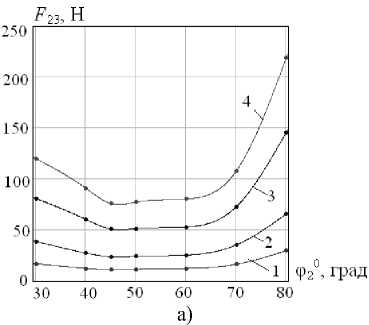
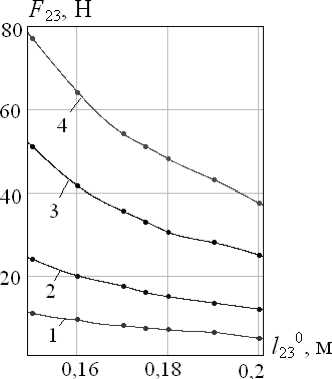
При фиксированной длине L прыжка сила F ₂₃ уменьшается практически пропорционально увеличению расстояния 1 ₂₃⁰ (рис. 4б). При угле наклона ноги ф₂⁰<45⁰ значение силы F ₂₃ убывает пропорционально увеличению ф₂⁰, а затем при 45⁰<ф₂⁰<80⁰ возрастает по некоторому криволинейному закону, приближающемуся к параболическому (рис. 4а). Чем больше требуемые значения высоты и длины прыжка, тем больше каждый из управляющих параметров.

T = m_t ( X 2 + y f)/2 + J ^p 2 /2 ,  ₍₂₎

где J ,, =1^3 = m i l i 2 /12, J ₄= m ₄( a ²+ b ²) - центральные моменты инерции звеньев, X. , y_t - проекции скоростей центров масс звеньев на оси системы координат.

а)

б)

Рис. 3. Графики зависимостей: а) F 23 (φ 2 ⁰), б) F 23 ( l 23 ⁰) при 1 – H =0.5 м, 2 – H =0,75 м, 3 – H =1 м

Выводы: в статье рассмотрен прыгающий робот, высота и длина прыжка которого являются управляемыми параметрами, предложена конструктивная схема устройства, позволяющая ему совершать серию прыжков независимо от приземления, разработаны технология реализации объектом прыжка и математическая модель движения робота. Выявлены зависимости между высотой и длиной прыжка и управляющими параметрами, которыми являются угол наклона ноги φ₂⁰, длина ноги, на которой происходит разгон l 23 ⁰, и сила F 23 , посредством которой осуществляется отрыв от поверхности. Полученные закономерности могут быть использованы при проектировании прыгающих роботов.

б)

Рис. 4. Графики зависимостей: а) F 23 (φ 2 ⁰), б) F 23 ( l 23 ⁰) при 1 – L =0,5 м, 2 – L =1 м, 3 – L =2 м, 4 –

L =3 м

Работа выполнена в рамках гранта РФФИ № 10-08-00769-а, госконтракта № П699 тема № 1.109.10ф, мероприятия 1.2.2 ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы.