Исследование дисперсности майонезной продукции с применением программы для ЭВМ

Введение. Майонез один из наиболее популярных продуктов, использующийся во многих блюдах в качестве заправки. Поскольку продукт популярен не только в нашей стране, но и в ряде других стран исследование свойств майонезной продукции необходимо, так же, как и системные исследования майонеза [1,2].

Одним из основных показателей майонезной эмульсии является ее дисперсность и жирность майонезной продукции. В настоящее время существует ряд стандартных методов определения дисперсности майонезной эмульсии, однако данные методы имею ряд своих недостатков таких как точность метода, влияние внешних факторов на процесс измерения дисперсности майонезной эмульсии и другие.

Материалы и методы. Исходя из этого существует необходимость создать новый точный метод определения дисперсности майонезной эмульсии, не зависящий от внешних факторов и наблюдателя. В основе нового метода лежит компьютерное зрение, в основе которого лежит алгоритм You Only Look Once (YOLO)[3,4,5]. Для нормальной работы нового алгоритма необходимо произвести ряд подготовительных этапов, а именно:

• •    Сделать не менее чем 2000-3000 тысяч изображений с объектом, который будет искать алгоритм. Поскольку на снимке с микроскопа жировых шариков майонеза достаточно много, то ориентировочное количество снимков с микроскопа будет варьироваться от 2 до 5;

• •    После получения снимков необходимо произвести аннотирование изображений

(рисунок 1). Аннотирование изображений проводится с помощью VGG image annotator. По своей сути аннотирование является указанием для нейросети, где на изображении находится искомый объект.

• •    После аннотирования изображений необходимо произвести дообучение заранее обученной модели. Поскольку 8 версии алгоритма предварительно обученных моделей 5, необходимо определить наиболее оптимальный вариант из данных моделей. Наиболее подходящей по все параметрам является yolov8n-seg. После подбора модели, происходит ее обучение на искомом объекте с разным количеством эпох [6].

  

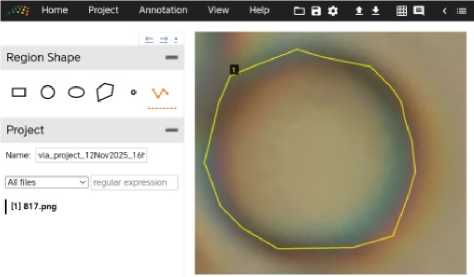
  Рисунок 1 - Аннотирование изображений жировых шариков

  
  

Для дальнейшей обработки полученных площадей жировых шариков майонеза применяется следующая методика, уже вшитая в программу:

Программа в автоматическом режиме составляет ряд данных, в нашем случае площади всех жировых шариков. После этого рассчитывается размах вариации (длинна общего интервала) как максимальное значение ряда минус минимальное значение ряда. Разбиение на частичные интервалы происходит с помощью формулы Стерджиса (1).

к = 1 + 3,3221lg (и)

где n - объем выборки (количество все жировых шариков).

Соответственно если количество интервалов вычисленное по формуле 1 получилось дробное, то его необходимо округлить до целого числа в большую сторону.

Поскольку длинны частичных интервалов число не постоянное, то применяют равно интервальную группировку. Равно интервальная группировка вычисляется как разность максимального и минимального значения ряда деленое на количество интервалов (2).

,   Хтах

h =---

—

xmin

к

где х _тах - максимальное значение ряда, x _m i _n - минимальное значение ряда

После вычисления равно интервальной группировки рассчитывается нижняя граница первого интервала соответственно, как разность минимального значения ряда и половины равно интервальной группировки как показано в феруле (3).

^xhi   ^xmin  2 ^hi

где xhi- нижняя граница первого интервала,^ - половина равно интервальной группировки.

Соответственно вариационный ряд будет начинается с x _h i с шагом h i . Шаг будет прибавляется до тех пор, пока не превысит значение максимального значения ряда.

После расчета параметров вариационного ряда с помощью библиотеки Plotly строится гистограмма частот в автоматическом режиме.

Однако полученные данные и поморённая гистограмма частот носит сугубо относительный характер так как размер жировых шариков привязан к размеру изображения. Для решения данной проблемы необходимо:

• 1)    При фотографировании жировых шариков наложить образцовое стекло с размеров ценой деления не менее 10 микрометров;

• 2)    Внести доработку в программу по автоматическому или же ручному поиску размерных рисок на изображении;

• 3)    Внести в автоматический пересчёт пиксельных размеров жировых шариков в микрометры.

Для корректной и хорошей работы программы наиболее целесообразно было использовать появившийся еще в 1991 году язык программировал Python поскольку данный язык программирования превосходно работает с файлами различных форматов и полной поддержке компьютерного зрения.

Результаты и их анализ. После проведения подготовительных этапов обученная модель подгружается в программу для ЭВМ. Однако совершенно необходимо определить при какой степени обучения модель будет работать с достаточной точностью. При использовании модели yolov8n-seg при разном количестве эпох обучения результаты будут иметь следующий вид, как показано на рисунке 2.

Однако использование текущего дата-сета и предварительно обученной модели yolov8n-seg недостаточно для полноценного использования поскольку практически нет отличий между 300, 500 и 700 эпохами обучения (рисунок 3.).

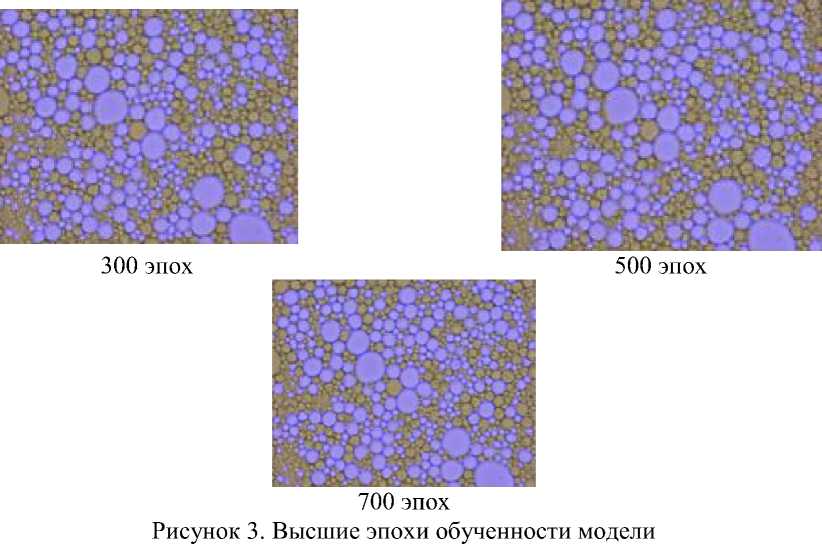
Выводы. Таким образом, для корректной работы программы для ЭВМ [7] необходимо дополнить или изменить аннотированный дата-сет из фотографий, а также сменить предварительно обученную модель на более мощную. В качестве новой предварительно обученной модели может выступать ряд моделей [8]:

• •    yolov8s - относится к классу небольших моделей, с баланса скорости и точности распознавания. Основными преимуществом является распознавание более мелких объектов, доступно больше классов для распознавания образов, работает быстрее на GPU по сравнению с предыдущей версией.

• •    yolov8m - относится к классу средних моделей по объёму. Основным преимуществом данной модели является большая точность по сравнению с предыдущими моделями. Однако данная модель требует больше ресурсов для обучения нежели предыдущие.

• •    yolov8x - относится к классу больших моделей. Основным преимуществом является самая высокая точность по сравнению с предшествующими моделями. Однако такая модель требует значительных ресурсов для обучения.

Стоит отметить, что дальнейший обсчет количества жировых шариков в настоящий момент не рационально так как обученная модель не обладает достаточной точностью.