Исследование движения плоского шестизвенного внутритрубного мобильного робота

Трубопроводы на сегодняшний день являются основными элементами систем транспортировки газообразных и жидких веществ, а также твёрдых веществ в виде раствора на большие расстояния. Так как подобные системы, как правило, устанавливаются под землей или внутри зданий, то существует проблема ограниченности доступа к трубам при выполнении работ по проверке состояния и поддержании их эксплуатационных свойств. Крайне актуальной задачей является разработка и изучение способов, позволяющих осуществлять мониторинг состояния внутренней поверхности трубопровода, поиск микротрещин, разрывов и т. д., не требуя при этом доступа к трубе на всей протяженности. На сегодняшний день разработан ряд различных подходов к перемещению внутри трубопроводов. Главным недостатком традиционных колесных и гусеничных систем является низкая проходимость в условиях загрязненности трубы [1, 2]. Наиболее перспективными являются многозвенные конструкции, копирующие змее- и червеподобные походки [3, 4], способные перемещаться в условиях загрязненности трубопровода, а также смены диаметра и поворотов.

В основе перемещения рассматриваемой в данной работе конструкции лежит принцип поочередной фиксации передней и задней пары звеньев (фиксирующих модулей) и перемещения центра масс робота при движении средней пар звеньев. Процесс фиксации внутри трубопровода подробно описан в работах [5, 6]. В данной же работе рассматривается движение средней пары звеньев робота внутри трубопровода.

Описание схемы робота. Рассмотрим конструкцию робота внутри трубопровода (рис. 1). Звенья 1 и 2 осуществляют фиксацию робота внутри трубопровода за счет сил трения. Точку А ₃ считаем неподвижной. Введем неподвижную систему координат с центром в точке А ₃, и повернутую на угол ζ относительно линии горизонта. Звенья 3 и 4

осуществляют перемещение переднего фиксирующего модуля (звенья 5 и 6) под действием крутящих моментов M 23 и M 34 . При этом звенья 5 и 6 не совершают движения между собой и поэтому рассматриваются в нашем случае как сосредоточенная масса, приложенная в точке А 5 . Примем, что центры масс звеньев A ₃ А ₄ и A ₄ А ₅ расположены в их геометрических центрах O 3 , O 4 . Введем подвижные системы координат X ₃ Y ₃ O ₃ и X ₄ Y ₅ O ₄ связанные с центрами масс звеньев. В точке А 5 действует приведенная сила F ₅ и приведенный момент M 5 , которые определяются путем приведения сил веса звеньев, а также сил инерции действующих на звенья 4 и 5.

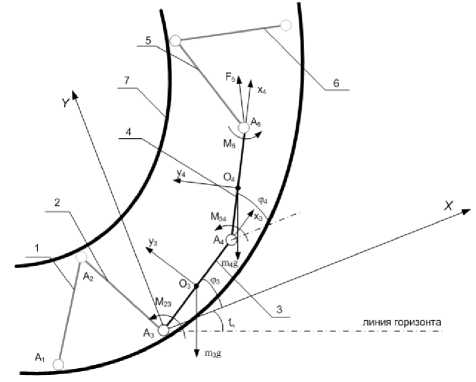
Рис. 1. Расчетная схема мобильного робота

Математическая модель движения робота. Для расчета кинематических параметров движения средних звеньев, в качестве обобщенных координат примем углы поворота обоих звеньев относительно их центров масс φ 3 , φ 4 и запишем систему дифференциальных уравнений, основываясь на уравнениях Лагранжа 2-го рода. При этом правые части уравнений получим методом возможных перемещений. После преобразований итоговая система дифференциальных уравнений описывающих движение третьего и четвертого звена робота примет вид:

Г               2 У 1                                    1             2 . Z

Ф 4 I ^J A, ⁺       I ⁺ - m 4 ¹ 3 ¹ 4 Фз ^COs( Ф з ^- ф 4 ) ^- - m 4 ¹ 3 ¹ 4 Ф 3 М<Ф 3

^- Ф 4) =

= M 34 ^- M 5 ⁺ F 5 ¹ 4 sm( a 5 ^- ф 4 ) ⁺ т 4 g — cos( ^ ⁺ Ф 4 )

А                                               2

ф ₃ ( J ^ + m ₄ 1 ₃ ² ) + 1 т ₄ 1 3 1 ₄ ф ₄ cos( ф ₃ - р ₄ ) + 1 m ₄ 1 3 1 ₄ф₄ sin( p ₃ - р ₄ ) =

= M ₂₃ + F 5 1 ₄ sin( a 5

^- Ф з ) ^{+ т} 4 g ¹ 4c ^{os( z +} Ф з ) ^{+ т} 3 g ^ c^{os( z +} Ф з )

Рассмотрим крутящие моменты между звеньями робота М23 и М34. В общем случае крутящий момент между звеньями можно описать следующим уравнением: Мi=Miдв – Мiсопр, где i – номер шарнира, Miдв – момент развиваемый электроприводом i-того шарнира, а Мiсопр – момент сопротивления движению звеньев. Представим момент сопротивления как: М!сопр = ^ • Ф4 + М!тр, где ^ - коэффициент вязкого сопротивления, Мiтр – суммарный момент силы трения. Опишем момент силы трения, согласно закону Кулона:

M ₁ ^тр . ^предsign( ф, ), если Ф , ^ 0;

M ^тр

м внеш , если ф_ = о и ^ м =неш| <  м ^тр.пред ;

M ²"р'е^1дп( ^ M °^неш ), если ^ = 0 ^ M °^неш| >  M тр пред,

где ΣМiвнеш – равнодействующая всех внешних моментов для i-того шарнира, кроме моментов сил сухого трения; Мiтр.пред – предельное значение силы трения, определяемая действующими силами в шарнире и коэффициентом силы трения, в данном случае, может быть определена экспериментально для конкретно взятого привода; Фi - скорость вращения звеньев для i-того шарнира.

О             2             4             6             8            1О ^ с

б)

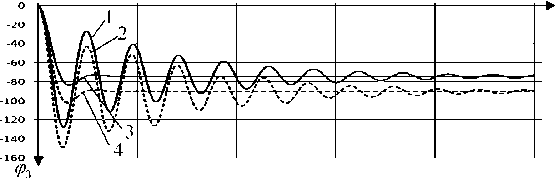
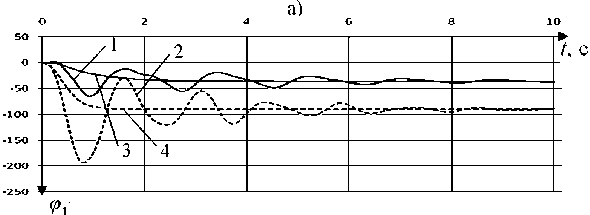
Рис. 2. Графики угла поворота звеньев под действие силы тяжести:

• а)    для третьего звена, б) для четвертого звена. 1 – угловое перемещение звена при коэффициенте силы вязкого сопротивления равном 0,001 и наличии момента силы трения в шарнире; 2 – перемещение при коэффициенте силы вязкого сопротивления равном 0,001, без силы трения; 3 – перемещение при коэффициенте силы вязкого сопротивления 0,01 и наличии момента сил трения в шарнире; 4 – перемещение при коэффициенте силы вязкого сопротивления = 0,01, без учета трения

Результаты численного моделирования. Наличие сил сухого трения в модели приводит к разрывному характеру правых частей системы уравнений, в том числе появляется режим останова звеньев, поэтому вычислительный алгоритм расчета содержит специальные блоки операций, позволяющих смоделировать такие эффекты. Для определения характера движения звеньев под действием силы тяжести и моментов сопротивления в шарнире, были получены зависимости углового перемещения от времени при различных параметрах системы (рис. 2).

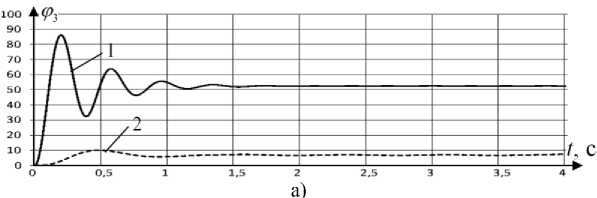
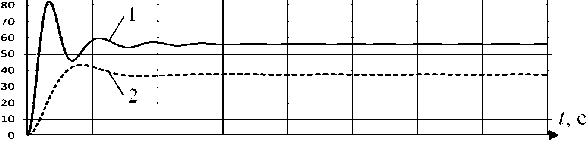
Покажем результаты моделирования движения звеньев под действием крутящих моментов электроприводов, задаваемых как: М дв = k дв ( φ i ^з –

φ i ^факт ), где k дв – моментный коэффициент, φ i ^з – задаваемый угол, φ i ^факт – фактическое значение угла. Покажем результаты моделирования при задаваемом угле для обоих звеньев φ_i ^з =60^о. Как видно из графиков, при малых значениях коэффициента усиления крутящий момент, развиваемый электроприводом, недостаточен для компенсации сил трения и сил тяжести. Однако увеличение коэффициента пропорциональности приводит к повышению колебательности системы, а следовательно ухудшению переходной характеристики. Далее покажем траектории перемещения точек А 4 и А 5 , при движении звеньев под действием крутящих моментов электроприводов. Точками показаны положения А 4 и А 5 в установившемся режиме.

90 кф₄

О           0,5         1           1,5         2           2,5         3           3,5

• б)

Рис. 3. Графики угла поворота звеньев под действие моментов развиваемыми приводами: а) третье звено, б) четвертое звено. 1 – коэффициент при системе управления k_дв =0,5; 2 – коэффициент при системе управления k дв =0,1.

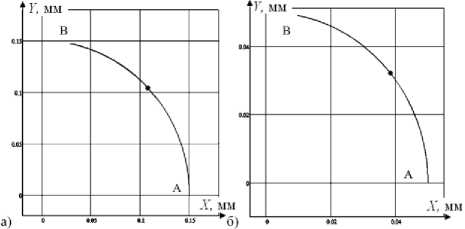
Рис. 4. Траектории движения точек А 4 (а) и А 5 (б) по действием крутящих моментов привода (движение происходит из точки А в точку В)

Выводы:

• 1.    Составлена математическая модель движения плоского шестизвенного внутритрубного мобильного робота, позволяющая описать различные режимы движения устройства, отличающаяся тем, что в модели учитываются силы сухого трения в приводах, сила вязкого сопротивления, а также взаимодействие звеньев робота с внутренней поверхностью трубопровода.

• 2.    Разработан алгоритм численного решения уравнений, позволяющий получить временные диаграммы и зависимости параметров определяющих характер движения звеньев робота.

• 3.    Установлено, что наличие сухого и вязкого трения в шарнирных соединениях робота существенно влияет на характер движения звеньев робота. Так, увеличение коэффициента вязкого трения в 10 раз снижает колебательность системы в 4-5 раз. В то же время введение

силы сухого трения обуславливает появление статической ошибки.

Работа выполнена в рамках реализации федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг (Соглашение № 14.132.21.1718).