Исследование гармонических колебаний полого цилиндра с винтовой анизотропией на основе трехмерных уравнений теории упругости

Основные соотношения линейной теории упругости для тел с винтовой анизотропией и результаты исследований задачи Сен-Венана для цилиндра с винтовой анизотропией опубликованы в [5–7]. В этих работах, в частности, показано, что при растяжении-сжатии цилиндра с винтовой анизотропией помимо продольных деформаций возникают сдвиговые и, наоборот, при кручении помимо сдвиговых — продольные.

В [8] для математического моделирования распространения пульсовых волн в артериальных сосудах на основе гипотез Кирхгофа — Лява получены уравнения колебаний оболочки с винтовой анизотропией. В [9] в рамках безмоментной теории исследованы некоторые особенности волновых процессов, порождаемых винтовой анизотропией. В [10, 11] анонсированы методы построения решений динамических краевых задач на основе прикладной теории типа Кирхгофа — Лява и результаты исследований некоторых конкретных задач, в [12] дается подробное описание этих результатов. Серия проведенных расчетов показала, что в осесимметричном случае винтовая анизотропия порождает связь между продольными и крутильными колебаниями, которая математически описывается амплитудными коэффициентами однородных волн.

Настоящая работа посвящена исследованию гармонических волн в полом цилиндре с винтовой анизотропией на основе трехмерных уравнений теории упругости. Также на основе полученных результатов анализируется область применения прикладной теории Кирхгофа — Лява (К.-Л.) и теории типа Тимошенко — Рейсснера (Т.-Р.).

• © 2011 Панфилов И. А., Устинов Ю. А.

• 2.    Основные соотношения теории упругости в винтовой системе координат и постановка задачи

Обозначим через r 1 , r 2 — внутренний и внешний радиусы цилиндра срединной поверхности оболочки, a — радиус срединной поверхности оболочки, h — ее толщину. С центром некоторого поперечного сечения цилиндра свяжем декартову систему координат Ox 1 x 2 x 3 , направив Ox 3 по оси цилиндра.

Введем винтовую систему координат r , ϕ, z, связанную c декартовой соотношениями x1 = r cos(y + tz),  x2 = r sin(^ + Tz),  X3 = z,

где r i 6 r 6 Г 2 ; T = tg(a)/a — геометрический параметр винтовой анизотропии.

Соотношения (1) при r = const, ^ = const являются параметрическими уравнениями винтовой линии. С каждой винтовой линией свяжем репер Френе с ортами главной нормали e 1 , главной нормали e 2 , касательной e 3 .

Переход от базиса Френе к базису винтовой системы координат er , eϕ , ez , первые два орта которой связаны с ортами декартовой системы Ox1x2x3 соотношениями er = i1 cos(^ + tz) + i2 sin(^ + tz), e^ = —i1 sin(y + tz) + i2 cos(^ + tz), осуществляется с помощью ортогональной матрицы

- 10  0

A =

0    — cos a sin a

0 sin a cos a где a = arctg(x), x = тr.

Будем считать материал цилиндра локально трансверсально изотропным, у которого направления главных осей тензора упругих свойств совпадают с направлениями ортов e 1 , e 2 , e 3 , где орт e 3 определяет направление оси упругой симметрии. В этом базисе соотношения обобщенного закона Гука имеют вид [13]:

° 11 = ^c 11 e 11 + ^c 12 ^e 22 + c 13 ^e 33 ,

^O 22 = ^c 12 e 11 ^{+ c} 11 ^e 22 ⁺ c 13 ^e 23 ,

^O 33 = ^c 13 ^{( e} 11 ^{+ e} 12 ) ^{+ c} 33 e 33 , 0 23 = ^c 44 ^e 23 ,   ^ 13 = c 44 e 13 ,   ^ 12 = ^c 66 ^e 12 •

Здесь e ij , σ ij — компоненты тензоров малых деформаций и напряжений соответственно, 2C 66 = C 11 — C 12 .

При переходе от базиса Френе к базису винтовой системы координат, как показано в [7, 8], для закона Гука получаем следующие выражения:

_a 0 = C 0 e ⁰ , C 0 = (c 0j ), i,j = 1,..., 6, ^{0    ( o} rr , ° фф , ^o zz ,° ^z ^,o rz ^,О Гф , ) , e   ^{( e} rr , ^е фф ,e zz , 2e ^z , ^{2 e} rz , 2e r^ ) •

Здесь c11 = c11, c1c = c12 l2 + c13 lS2, c13 = c13l2 + c12l2, c14 = lcls(c13 — c12), c22 = c11 l4 + (2c13 + 4c44) lc ls + c33l4, c23 = c13l4 + (c11 + c33 — 4c44) lCl2 + c13l4, c24 = — c11lcls — c13 (lcl3 — lcls) + c33lcl3 — 2c44 (lcl3 — lcls), 0

^c 33 = ^c 11 l s ^{+ 2 c} 13 l c l s ^{+ c} 33 l c ⁺ 4c 44 l c l s , ^c 34 = ^— l c l s ⁽ c 11 l ^{2 — c} 13 ^{+ 2 c} 13 l ^{2 + 2 c} 44 l ^{C — 2 c} 44 l ^{2 )} , 0       22      22     22           22

^c 44 = ^c 11 ^l _c ^l _s ^{— 2 c} 13 ^l _c l _s ^{+ c} 33 l _c l _s ^{+ c} 44 ⁽ 1 ^{— 4} l _c l _s ^{) ,} 0              2           20                                        0              2           2

c55 = c44lc + c66ls ,   c56 = lcls(c44 — с66)   c66 = c66lc + c44ls , lc = cos a, ls = sin a.

Остальные элементы матрицы C ⁰ равны нулю.

В базисе винтовой системы координат er , eϕ , ez компоненты тензора деформаций выражаются через координаты вектора смещений u = (Ur ,Uv,Uz )T следующими формулами:

e rr — ^dr u r , e mm — ² e rm — ^d r ^u m ^{+ ( d} m ^u r

(u r + d _v u_v)/r,

e zz — Du z ^,

-

u ^ )^/r,   ^2e rz

dr uz + Dur,(4)

²e z^ — ^d m ^u z ^{/r +} Du m *

Уравнения движения в данном случае имеют вид:

dr (r^rr) — ст^^ + d^Or^ + rDarz = —prd^Ur, dr (ror^) + OrV + dvovv + rDn.z = —prd^u^,(5)

d r (rCT rz ) + d ^ o ^z + rDCT zz = —prdtu _z .

В формулах (5) ρ — плотность материала цилиндра;

d r = тг,   д _ф = ^-,   d z = ^-,   d t = ^D = d z — тд ^ .

∂r        ∂ϕ ∂z∂t

Будем считать, что боковая поверхность цилиндра свободна от напряжений при r = re (в = 1, 2) :   Qrr = CTrm = ^rz = 0*

Для исследования гармонических волновых процессов в цилиндре будем использовать различные операторные формы [15]. Для этого введем следующие векторы:

^CT r — ( ^CT rr ^,CT rm ^,CT rz ) , ^CT m — ^{( CT} rm ^,CT mm ^,CT zm ⁾ , ^CT z — ( ^CT rz ^,CT zm ^,CT zz ) *

Используя соотношения (3), (4) и ограничиваясь осесимметричным случаем, представим σ _r , σ ϕ , σ _z в виде:

	a r — d z A r u	+ B r u, a ^	— d z A v u + B v u,	a z — d z A z u + B z u.	(7)
Здесь
	0     C*14	c 0 13	c 11 d r + c i2 /r	00
	A r —    c 56    0	0    ,    B r	—       0	c 66 ( d r — 1 /r ) c 56 d r	,
	c 55    0	0	0	c 0 56 ( d r — 1 /r ) c 55 d r
	c 56    0	0	0	c 66 ( d r — 1 /r ) c 56 d r
	A v —   0  c ^4	c 0 0 23    ,   B ϕ	—    c 12 d r + c' 22 /r	00	,
	0   c 0 44	c 0 34	C 14 d r + d 24 /r	00
	c 0 56     0	0	0	c 56 ( d r — 1 /r ) c 56 d r
	A z —    0   c 0 44	c 0 34    ,   B z	—   c 0 14 d r + c' 24 /r	00	.
	0    c 34	c 0 33	c 13 d r + c 23 /r	00

В этой работе остановимся на осесимметричных колебаниях. Отыскивая решение в виде гармонической волны u — ei(kz-^t)a, ar — ei(kz-^t)br,   ^ — , i(k- -t b^, a. — ei(kz-^t)bz, a — (ar ,ia^ ,iaz) , br — (ibrr ,br^,brz) , b^ — (br^, ib^^Vib^z) , bz — (brz ,ib^z ,ibzz) , на основании (5), (6) получаем двухпараметрическую спектральную задачу

L(k, w)a = — k ² A 2 a + ikA 1 a + A o + rpw ² Ia — 0                 (8)

при r — r e : (ikA _r + B r ) a — 0.                          (9)

Здесь

A 2 a — rA _z a, A 1 a — d r (rA r a) + SA ^ a + rB _z a, A o — d r (rB r a) + SB ^ a,

	0 — 10		100
S—	1   0 0	, I —	010
	000		001

• 2.1.    Основные соотношения прикладной теории, основанной на гипотезах Кирхгофа — Лява. Известно [14], что классическая теория оболочек Кирхгофа — Лява (К.-Л.) основывается на двух основных гипотезах, которые в рассматриваемом случае формулируются следующим образом:

• 1)    абсолютные значения напряжений a _rr ,a _rz ,a _r^ ^ a_w,a ^_z , a _zz , в силу чего в соотношениях закона Гука первыми тремя можно пренебречь;

• 2)    прямые углы между нормалью к срединной поверхности оболочки до деформации остаются таковыми и после деформации.

В соответствии с этими гипотезами основные соотношения принимают следующий вид:

Ur — u0 (y,z), u^ — u^(^,z) + a6v, Uz — u0 (^,z) + a^z, 6V — —a-1(d^ur — u^), 6z — —Duz, —h/2 6 a 6 h/2, где ur0 , u0ϕ , uz0 — смещения точек срединной поверхности; θϕ , θz — углы поворота нормали. Соответственно, компоненты тензоров деформаций и кривизны имеют вид:

e_w = e^ + a K ^^ , e zz — e^ + a K zz , e ^z — e ^ + a K ^z , 0       -1   0        0       0         0       0          0     -1     0

e rz — er^ — 0, e 22 — a (u r ^{+ d} ^ u ^ ),   e zz — Du z , 2e z^ — Du ^ ⁺ a ^d ^ u z ,     ⁽¹¹⁾

^K 22 — a ^{( d} 2 ^U 2   ^d 2 u r ), ^K zz — D u r , 2 ^K z^ — a Du ^  ² a D^d ^ u r .

В качестве основных характеристик напряженного состояния введем усилия и моменты

T i — hc j e j , M i — h ³ c ij e 1 /12 (i,j — 1, 2, 3).

Здесь и ниже — суммирование по повторяющемся индексам;

T 1 — T_w.

T₂ — T, zz ^,

T 3 — T ^z ,

M l — M .. , M 2 — M zz ,  M 3 — M ^z ,

00  00 00

el e^^, e2    ezz, e3 e^z, el — кфф,  e2 — Kzz,  e3 — k^ .

Используя вариационный принцип Гамильтона и считая независимыми вариациями δu _r ⁰ , δu ⁰ _ϕ , δu _z ⁰ , получаем следующие уравнения движения:

DT 2 + а ^-1 д ^ Т з - hpd t u z — 0, a ^-1 d ^ T i + DT 3 + a ^-1 Q i - hpd _t ² u _v — 0, a ^-1 d ^ Q i + DQ 2 - a ^-1 T i - hpd 2 u _r — 0. Q i — DM 1 + a ^-1 d ^ M 3 , Q 2 — DM 3 + a ^-1 d ^ M 2 ,

здесь Q 1 , Q 2 — поперечные силы.

• 2.2.    Основные соотношения прикладной теории, основанной на гипотезах Тимошенко — Рейсснера. Для повышения точности расчетов в прикладной теории Тимошенка — Рейснера (Т.-Р.) допускаются искажения прямых углов между нормалью и срединной поверхностью, в силу чего углы поворота нормали θ ϕ , θ _z становятся новыми дополнительными неизвестными, а в выражениях обобщенного закона Гука (3) следует положить только CT _rr — 0. При этом основные соотношения принимают вид:

U r — u 0 (^,z), u _v — u ^ (^,z)+ a6 _v , U z — U 0 (^,z) + a^ z ,            (13)

ew — e^ + aK^^, ezz — e0z + aKzz, e^z — e°z + aK^z, erz — erz + aKrz, er^ — er^ + aKr^, ew — a-1(ur + d^u°), ezz — Du0, 2e% — Du° + a-1d^u0, kvv — a-2(d^u° - d2u0), Kzz — -D2uz,                    (14)

2 K z_V — a ^-1 u 2 - 2Dd _v u 0 ,

2e rz — 9 z + Du r ,   2 K rz — 0,

^2e r2 — ^ 2 ⁺ a ^(d 2 ^U r ^U 2 ⁾, 2^K r2 — ^a 9 ф .

Основными характеристиками напряженного состояния по-прежнему остаются усилия и моменты, а соотношения обобщенного закона Гука принимают вид:

T i — hc ij e j ,   M i — h ³ c ij e i /12 (i — 1, 2, 3; j — 1, 2, 3,4, 5).

T 1 = T_w, T 2 = T zz , T 3 = T ^z , Q 1 = hC 5j e j , Q 2 = hc 4j e j ,

M l = M_w,

00  00

el    eW1   e2    ezz, el = kw,  e2 = Kzz,

M2 = Mzz, e3    e^z, e3 = K^z,

M 3 = M ^z , 00 00

e4    erz ,   e5    er^, e4 = Krz,   e5 = Кгф.

На основании вариационного принципа Гамильтона, считая независимыми вариациями δu _r ⁰ , δu ⁰ _ϕ , δu _z ⁰ , δθ _z , δθ ϕ , получаем следующие динамические уравнения:

DT2 + a 1дфТз — hpo d^Uz = 0, a 1 d^Ti + DT3 + a 1 Qi — hpodt u^ = 0, a 1dmQi + DQ2 — a 1 Ti — hpod2ur = 0,

• _{-                 h 3}                                    (15)

• 3.    Построение дисперсионных кривых

DM2 + a ld^M3 — Q2 — — podt9z = 0, h3

DM 3 + a d ( MM— — Q i — — p o d t 9 ^ = 0.

Для проведения исследований перейдем к безразмерным координатам £ = r/r 2 , Z = z/r 2 и введем параметры 7 = r 2 k — безразмерное волновое число, Q = Г 2 ш/с — безразмерная частота, c = (E 0 /p) ^{1 / 2} — параметр, имеющий размерность скорости. Все модули отнесем к E ⁰ .

Расчеты проводились для материала со следующими техническими константами (биологическая ткань стенки артериального сосуда [3]):

E 0 = 4.905 • 10 8 , E = 0.833 • E', G = E 0 /6, v 0 = 0.45, v = 0.54.

Замечание. Метод получения и особенности спектров волновых чисел для гипотез Кирхгофа — Лява и Тимошенко — Рейсснера подробно описан в [9, 12].

Как следует из общей теории твердых волноводов [15] корни дисперсионного уравнения расположены симметрично в комплексной плоскости y = а + ie. Расчеты показали, что для осесимметричного случая при низкочастотных колебаниях (Q ^ 1) для теории на основе гипотез Кирхгофа — Лява спектр волновых чисел состоит из двух пар вещественных волновых чисел y ± = ± Y 1 (Y 1 > 0), Y ± = ± Y 2 (7 2 > 0) и четырех комплексных

Y+ = 73 = аз + ie3 , 7+ = 74 = —73 , 7- = "Уз, 7- = —73, где а3 > 0, в3 > 0. Для теории Тимошенко — Рейсснера добавляется еще одна пара комплексных корней: 7+ = 75 = а4 + ie4, 7- = "/5.

Перейдем к описанию метода построения дисперсионных кривых на основе трехмерных уравнений теории упругости.

Спектральную задачу (8) преобразуем к безразмерному виду

L(7, ^)a = ( — 7 ² A 2 + i7Ai + A o + ^G 2 I)a = 0 при ^ = ^ _a : (i7A _r + B 'r )a = 0.

Здесь матрицы A j получаются путем деления элементов матриц A j на E', заменами r _a = Г 2 ^ _а , d r = ^д ^ (а = 1, 2), д^ — обыкновенная производная по £.

Дисперсионные кривые для трехмерного случая были получены на основе численного интегрирования спектральной задачи (16) «методом пристрелки». Для реализации метода эта задача была преобразована в краевую задачу для системы обыкновенных дифференциальных уравнений первого порядка следующего вида:

— = G il a + G 12 b,   =— G 21 a + G 22 b,  ^{b (} € 1 ) = 0,  ^{b (} ^ 2 ) = 0,

dξ                  dξ где b = ^br. Выражения для матриц Gj здесь не приводятся ввиду очевидности способа их построения на основе вышеприведенных формул.

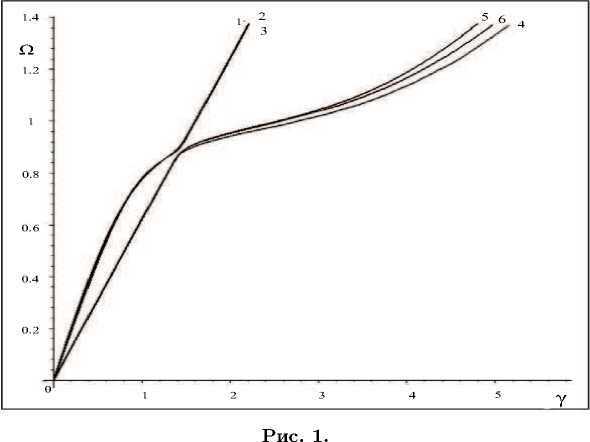
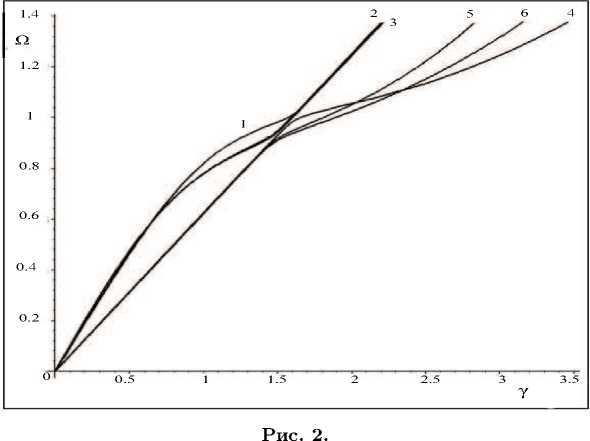
На рис. 1 и 2 приведены графики первых двух дисперсионных кривых для £ i = 0.9, ^ 2 = 1 (оболочка средней толщины) и ^ i =0.1, ^ 2 = 1 (толстая оболочка) соответственно; а = 45 ° .

Здесь кривые 1, 4 отвечают трехмерной теории, кривые 2, 5 — теории К.-Л., кривые 3, 6 — теории Т.-Р. Кривые 1-3 отвечают при x = 0 квазипродольным волнам, т. е. тем волнам, которые при x = 0 (когда винтовая анизотропия отсутствует), являются продольными. Кривые 4–6 отвечают квазикрутильными волнам, т. е. тем волнам, которые при x = 0 оказываются крутильными. На рис. 1 для данного диапазона частот первые три дисперсионные кривые сливаются.

Как и следовало ожидать, результаты, полученные на основе теории Т.-Р., более близки к трехмерной теории, чем результаты, полученные на основе теории К.-Л. Также видно, что увеличение толщины ведет к большему расхождению результатов. Эти графики позволяют получить некоторое представление об области применимости прикладной теории Кирхгофа — Лява и теории Тимошенко — Рейсснера. Так, например, прямолинейный участок рис. 1 первой дисперсионной кривой принадлежит области 0 6 y 6 Y * = 0.7, 0 6 Q 6 Q * = 0.9, второй дисперсионной кривой — 0 6 y 6 Y * = 0.9, 0 6 Q 6 Q 1 = 1.5. Из этих неравенств можно сделать вывод о том, что для цилиндра, с выбранными параметрами, прикладная теория К.-Л. и теория Т.-Р. будет давать удовлетворительные результаты, если круговая частота ш <  C 1 Q * /а.

Поскольку множество собственных частот Q n (n = 1, 2,...) неограничено и принадлежит дисперсионным кривым, то данная прикладная теория может претендовать на достаточно точное определение только тех частот, значения которых принадлежат диапазонам 0 6 Q n 6 Q * , 0 6 Q n 6 Q * .

• 4.    Критические частоты и высокочастотные колебания

Волновые процессы с круговой частотой Q > Q * условно будем называть высокочастотными.

Под «критическими частотами» в данном случае понимается множество СЗ ш i (l = 1, 2,...) самосопряженной спектральной задачи

L(0, ш)а = A o + грш ² 1а = 0 при r = r e : B _r а = 0,              (19)

которая является частным случаем задачи (8), если в последней положить к = 0.

Теории, основанные на гипотезах Кирхгофа — Лява и гипотезах Тимошенко — Рейсснера, позволяют получить только первую критическую частоту и первые три критических частоты соответственно.

В таблице 1 в столбцах приводятся значения первых трех критических частот при a = 45 ° для различных толщин (€ 2 = 1, € 1 — варьируется).

Таблица 1

трехмерная теория		теория Т.-Р.		теория К.-Л.
€ 1 = 0.9 € 2	€ 1 = 0.7 € 2	€ 1 = 0.9 € 2	€ 1 = 0.7 € 2	€ 1 = 0.9 € 2	€ 1 = 0.7 € 2
1.44	1.39	1.45	1.20	1.45	1.22
17.23	5.81	13.12	4.48	-	-
19.51	6.59	15.19	5.07	-	-

Для трехмерной теории критические частоты были полученны путем численного интегрирования уравнений (18). Для контроля точности результатов, полученных численным методом, поставленная задача (4)-(6) при к = 0, a = 0 (трансверсально-изотропный материал) была решена аналитически. Сравнительный анализ показал полное совпадение результатов, а также позволил идентифицировать типы колебаний, отвечающих каждой из приведенных частот. При изменении параметра α первая частота порождает ветвь квазипродольных колебаний, вторая — квазирадиальных, третья — квазикрутиль-ных.