Исследование газодинамического потока и конструкции в модельной экспериментальной установке

Аэроупругие явления могут приводить к отказам в работе энергетических установок ракет, самолетов, к разрушению строительных конструкций, трубопроводов различного назначения и т. д. Опасность аэроупругих явлений приводит к непрогнозируемым последствиям, которые можно обнаружить только на этапе создания натурного образца. Многовариантность конкретных реализаций аэроупругих процессов, а также сама сложность эти явлений предполагает необходимость прогноза, который может быть осуществлен с помощью вычислительного эксперимента. Для повышения надежности прогнозирования необходима верификация расчетных методик, но с использованием, по-возможности физического модельного эксперимента. В то же время недостаточно существующих расчетно-экспериментальных методик. Данная статья описывает процесс создания и использования расчетно-экспериментальных методик оценки колебательных процессов в аэроупругой постановке с использованием Супер ЭВМ.

Цель работы: создание и отработка методики исследования аэроупругих процессов на базе расчетно-экспериментального комплекса с использованием Супер ЭВМ.

Большинство методик исследования аэроупругих явлений используют одно- и двухмерные модели, чаще в стационарной и квазистационарной линейной постановке, и базируются на использовании волнового уравнения. В целом принимается, что развитие колебаний зависит от относительного вклада различных физико-химических процессов, способствующих усилению, либо демпфированию возмущений. Обычно принимается, чтогаз воздействует на конструкцию, но необходим учет и их взаимовлияния. Кроме того, имеющиеся методики не могут объяснить влияние жесткостных и массовых характеристик, условий закрепления конструкции на колебания давления в ЭУ [1].Особый интерес представляет поиск механизмов возникновения быстропротекающих колебательных процессов, характерное время которых имеет длительность, соизмеримую со временем распространения возмущения в конструкции.

1.    Теоретическая часть 1.1.    Газодинамический расчет

Сформулирована следующая физическая постановка задачи:

• -    процессы рассматриваются трехмерными динамическими; в качестве рабочего тела выбран воздух, который рассматривается как сжимаемый; стенки модельной камеры

непроницаемые, нетеплопроводные; в начальный момент времени модельная камера заполнена воздухом, значение давления для первого варианта равно 0,3 МПа; для второго варианта – 0,1 МПа, температура воздуха – 293 К [2].

Математическая модель движения газа – это система уравнений в частных производных, включающая в себя законы сохранения массы, импульса, энергии и уравнение состояниягаза. Математическая модель может быть модифицирована через интерфейс Ansys CFX.

Рассчитываемыми переменными математической модели являются векторные и скалярные поля, разделяемые на независимые и зависимые переменные. Независимые пе- ременные определяются из решения систем уравнений с совокупностью начальных и граничных условий, а зависимые выражаются через них.

Выбранная математическая модель включает в себя следующие соотношения:

• -    закон сохранения массы

^ ^{+ v} (p^y) = 0

закон

сохранения импульса

Т7

-^ + V (py ® У) = —vp + v ((д + u t ) ( v y + ( v y) )J

-

закон сохранения энергии

¥ ,„ ,„„ =   „ (g + Pj . )„)

где t - время; p - плотность; У - скорость; P - давление; p - динамическая вязкость; p _t

• -    турбулентная динамическая вязкость; H - энтальпия; с _р - теплоемкость; Л - коэффициент теплопроводности; Pr _t - турбулентное число Прандтля.

Используется известная к — £ модель турбулентности. Вводятся следующие соотно- шения:

^£Gpk2 -^v 'p^k' = ^{v (}(p ⁺ ^ ; ) ^{v k})

+ p t G ^— p^£

^⁺’ (p^ =’ (("⁺£) ’ i

+ C, ^G - C ₂ f _1P^

где ^G = ^5? D

= ^{S -} 1 (’^ ⁺ ;;И - ^S = 5; ⁺ S " * ^{= 1}a = 13 с = 1А4.. ^сг =

1,92 , f , = 1 , k - турбулентная энергия, e - скорость диссипации турбулентной энергии, G

• -    определяет скорость генерации турбулентной энергии, Sq - удвоенный тензор скоростей деформации.

Уравнение турбулентной вязкости вычисляется по формуле Колмогорова-Прандтля: k ²

Ft = с^р— где С^ = 0,09 - константа.

- уравнение состояния

Р = pRT где R - универсальная газовая постоянная.

Математическая модель замыкается начальными и граничными условиями.

• 1.2.    Расчет напряженно-деформированного состояния конструкции

Сформулирована следующая физическая постановка:

• -    конструкция рассматривается трехмерной; исследуется модельная камера, физикомеханические характеристики и геометрические параметры которой, можно изме-нять;материал модельной камеры – упругий, однородный.

Модальный анализ служит для определения собственных частот и форм колебаний конструкции.Результаты анализа дают возможность установить число форм колебаний и шаг интегрирования по времени, что может обеспечить надежное решение задачи о динамическом поведении системы в неустановившемся режиме.

В программе Ansys Workbench модальный анализ – это решение задачи о свободных (невынужденных), затухающих или незатухающих, колебаниях дискретной системы, которая описывается следующим уравнением движения:

[М]{и"} + [С]{и ' } + [К]{и} = 0

где [М] - матрица масс; [С] - матрица демпфирования; [К] - матрица жесткости; {и"} -вектор узловых ускорений; {и ’ } - вектор узловых скоростей; {и} - вектор узловых перемещений.

Этому уравнению придается форма, соответствующая задаче о собственных значениях. Для случая незатухающих колебаний (наиболее типичного для модального анализа) пренебрегают слагаемым [С]{и ' }, и уравнение приводится к виду

([К] - ^ ² [М]){и} = 0

где ш ² - (квадрат собственной частоты) - собственное значение, {и}- собственные формы колебаний, не являющиеся функциями времени.

Допущения при расчете свободных колебаний:

• -    матрицы [К] и [М] являются константами, что означает следующее:

• -    принимается линейное упругое поведение материалов; используется теория малых деформаций, не учитываются нелинейные эффекты; матрица [С] отсутствует, значит не учитываются эффекты демпфирования; вектор сил {F} отсутствует, значит не рассчитывается возбуждение конструкции внешними силами; закрепление конструкции не является обязательным условием расчета, как в задачах статики;форма свободных коле-

• баний вычисляется в относительных единицах и не позволяет определить абсолютные смещения.

Анализ гармонического воздействия используется для определения параметров установившегося движения линейной системы при синусоидальном силовом возбуждении. Этот вид анализа актуален при исследовании влияния нагрузок, меняющихся во времени по гармоническому закону.

Разрешающее уравнение для этого вида анализа представляет собой специальный случай общего уравнения движения, в котором вынуждающая сила {F ( t ) } является синусоидальной функцией времени с известной амплитудой F _o , частотой ш и фазовым углом ф :

{F ( t ) } = ^F _o (cos(tit) + ф) + i sin((Mt) + ф)}

Перемещения меняются синусоидально с частотой ш, но не обязаны совпадать по фазе с вынуждающей силой. Нагрузки могут быть в форме узловых сил, начальных перемещений или распределенными по элементу. Для заданной частоты пользователь имеет возможность найти перемещения либо в виде набора амплитуд и фазовых углов, либо в виде реальной и мнимой частей решения.

Для проведения гармонического анализа доступны три метода: полный, редуцированный и метод суперпозиций. Полный метод предполагает использование полных, возможно, несимметричных, матриц [F], [М] и [С]. Это делает возможным выполнение некоторых сложных видов гармонического анализа в области акустики, пьезоэлектричества и динамики вращающихся валов. Этот метод анализа является одношаговым. Метод приведения (редуцированный) и метод суперпозиции форм колебаний можно использовать для линейных задач, приводящих к симметричным матрицам. Редуцированный метод основан на сокращении матриц [К], [М] и [С] способом приведения Гуяня и дает решение за два шага (решение приведенного уравнения движения и затем повторный проход - шаг расширения решения). Многошаговый метод суперпозиции требует предварительного проведения модального анализа для выполнения следующих шагов решения.

Математическая модель замыкается граничными условиями.

При анализе свободных колебаниймеханические и тепловые нагрузкине задаются. Можно задавать способ закрепления конструкции. Используется фиксированное закрепление модельной камеры – FixedSupport (жесткая заделка). При проведении гармонического анализаприложим циклические перемещения (Displacement)к торцу модельной камеры. Амплитударавна 1 мкм.

2.    Проведение вычислительных экспериментов

При подготовке и проведении вычислительного эксперимента использовалась система инженерного анализа Ansys.

Ansys – программный пакет конечно-элементного анализа, решающий задачи в различных областях инженерной деятельности (прочность конструкций, термодинамика, динамика жидкостей и газов, электромагнетизм), включая связанный междисциплинарный анализ.

При проведении вычислительных экспериментов использовался кластер Пермского национального исследовательского политехнического университета (ПНИПУ), имеющий следующие технические характеристики:

- 88 вычислительных узлов; 128 четырехядерных процессоров «Barcelona-3» (всего 512 ядер); 48 восьмиядерных процессоров «IntelXeon E5-2680» (всего 384 ядра); пиковая производительность 20 Тфлопс; производительность в тестовом пакете Linpack 78%; объем системы хранения информации 12 ТБ; объем оперативной памяти 128 Гбайт/узел; операционная система Windows HPC Server 2008; 13-е место в рейтинге ТОП-50 в СНГ (по состоянию на 01.09.2008г.).

Было получено ускорение (рис. 1), рассчитанное при использовании параллельного алгоритма для р процессоров, по сравнению с последовательным вариантом выполнения вычислений, определяемое по формуле

Sp (п) = Тг(п)/Тр (п), где величина п используется для параметризации вычислительной сложности решаемой задачи и может пониматься, например, как количество входных данных задачи, Тт(п) -время последовательного решения задачи на ЭВМ, Тр(п) - время выполнения алгоритма на р процессорах.

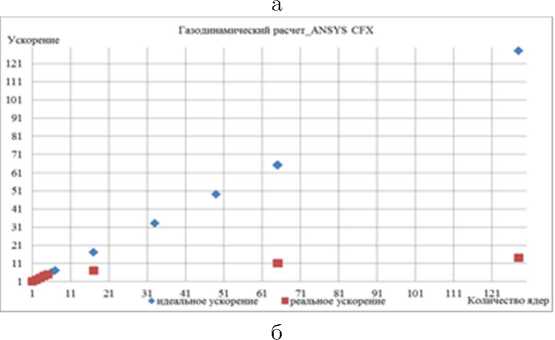
Рис. 1 . Ускорение при использовании параллельного алгоритма: а – прочностной расчет; б – газодинамический расчет

Проведена проверка сходимости решения на сгущающихся сетках.

Для верификации расчетов междисциплинарных аэроупругих задач была разработана модельная экспериментальная установка (рис.2). Установка состоит из модельной камеры, основания, генератора колебаний, системы регистрации и измерения National Instruments. В качестве чувствительных элементов используются высокочастотные вибродатчики с рабочим диапазоном частот от 0 до 100 кГц и датчики давления, работающие в диапазоне частот от 0 до 40 кГц.

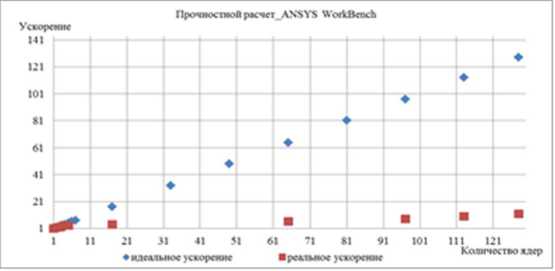
Рис. 2 . Конструктивная схема экспериментальной установки:

1– корпус, 2, 3 – крышки, 4, 5 – штуцеры, 6 – сменные элементы

При этом потребовалась реализация следующих этапов проведения физического эксперимента: анализ характерных геометрических размеров исследуемого объекта, физико-механических характеристик материалов, из которых данный объект изготовлен, конструктивных особенностей, значимых с точки зрения колебательных процессов, анализ действующих нагрузок, создание виртуальной модели объекта физического эксперимента, вычислительный эксперимент по оценке собственных и вынужденных колебаний, верификация, анализ результатов вычислительного и физического экспериментов.

3.    Экспериментальная часть

Для проведения экспериментальных исследований влияния физико-механических характеристик материала конструкции на характеристики резонансных колебаний необходимо было подобрать такие геометрические и массовые характеристики модельной камеры, чтобы был обеспечен резонанс модельной камеры и газовой полости.

Задавались следующие исходные данные:

Исходные данные для вычислительного эксперимента

Таблица 1

Материал	Сталь i = 1	Титановый сплав i = 2	Алюминиевый сплав i = 3
Толщина оболочки, 5, м	0,001	0,001	0,001
Длина оболочки, L , м	1	1	1

В результате расчетов определеныт р _ез :

• -    для стали ( i = 1 ): т р _ез = 24,27 кг ;

• -    для титанового сплава (i = 2 ): т р _ез = 12,14 кг ;

• -    для алюминиевого сплава (i = 3 ): т р _ез = 8,5 кг .

Вместе с тем проведены численные расчеты для труб со следующими характеристиками:

Таблица 2

Характеристики модельной камеры

Материал	Сталь i = 1	Титановый сплав i = 2	Алюминиевый сплав i = 3
Толщина оболочки, 5, м	0,001	0,001	0,001
Длина оболочки, L, м	1	1	1

В результате численных расчетов в Ansys Workbench определены f p_e3 : для стали (i = 1 ): Г рез = 367 Гц ;

для титанового сплава (t = 2 ): / р^з = 333 Гц ;

для алюминиевого сплава (t = 3 ): /е з = 350 Гц .

Физический эксперимент показал следующие результаты:

• -    для корпуса из алюминия резонансная частота для конструкции находится в пределах от 250 Гц до 350 Гц, а для газа от 200 Гц до 400 Гц;

• -    для корпуса излатуни резонансная частота для конструкции находится в пределах от 350 Гц до 550 Гц, а для газа от 200 Гц до 400 Гц;

• -    для корпуса из меди резонансная частота для конструкции находится в пределах от 700 Гц до 850 Гц, а для газа от 200 Гц до 350 Гц;

• -    для корпуса из стали с толщиной стенки 0,5 мм резонансная частота для конструкции находится в пределах от 700 Гц до 900 Гц, а для газа от 200 Гц до 350 Гц [3].

Заключение

• 1.    Принят и реализован комплексный подход к вычислительному моделированию работыэкспериментальной установки: исследованы как газодинамические процессы, так и напряженно-деформированное состояние конструкции.

• 2.    Разработаны физическая и математическая постановки и 3D модели рабочей камеры экспериментальной установки для оценки газодинамических параметров и компонент и оценке напряженно-деформированного состояния вычислительного эксперимента в системе инженерного анализа Ansys.

• 3.    Подготовлены и проведены газодинамические и прочностные вычислительные эксперименты, в ходе которых рассмотрены переходные процессы в модельной камере для нескольких вариантов ее исполнения.

• 4.    Проведен анализ собственных и вынужденных колебаний модельной камеры. Определены формы и частоты собственных колебаний конструкции. Определены формы, амплитуды и частоты вынужденных колебаний.

• 5.    В ходе анализа напряженно-деформированного состояния конструкции модельной камеры получены поля перемещений, деформации и напряжений.

• 6.    Разработана конфигурация системы измерения и регистрации экспериментальной установки с использованием оборудования фирмы National Instruments и программного обеспечения LabVIEW.

• 7.    Подготовлены и проведены физические эксперименты, в ходе которых подтверждена работоспособность основных элементов экспериментальной установки; проведено исследование сигналов вибродатчиков, датчиков давления, установленных вдоль образующей модельной камеры; выявлено резонансное взаимодействие корпуса установки и газовой полости на частоте около 300 Гц.

• 8.    Обнаружено, что масштабируемость прочностного расчета ниже, чем при оценке газодинамического процесса. Предварительный анализ показал, что скорость расчета газодинамических процессов повышается при оптимизации процессов распараллеливания и построения сетки. Масштабируемость по оценке напряженно-деформированного состояния конструкции при этом не повышается. При решении связанных задач, применительно к динамическим системам «газ-конструкция» в системе инженерного анализа Ansys возможно, что продолжительность расчета окажется неприемлемой. Для решения такого рода задач, возможно, потребуется разработка новых алгоритмов.