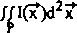1(х) = ( 1
[ 0, иначе, соответствующей равномерно засвеченному прямоугольнику размером 2at х 2а2,где х = (х, у) - декартовы координаты в фокальной плоскости.
Пусть w0(u) - факторизуемая функция; w0(u) = wQJ(u)w02(v), то есть AQ(u) = A0|(u)AQ2(vX¥>0(u) = ч»01 (u) + + ^02^v^’ тогда фазовую функцию оптического элемента можно представить в виде:
>p(u, v)= ^(u) + <^2(v), (1)
где i/^ (u), t?2(v) ~ фазовые функции цилиндрических (линейных) оптических элементов, преобразующих одномерные пучки с комплексными амплитудами wQ1(u) и wQ2(v) в отрезки с постоянной интенсивностью с длинами 2а, и 2а2 соответственно.
Расчет фазовой функции ^, (u) [<р2 (v)] цилиндрического оптического элемента основан на алгоритме Гершбер-га-Секстона с использованием в качестве начального приближения геометрооптической фазовой функции ^](и) фокусатора в отрезок и методе фазового кодирования амплитудных функций [4].
В параксиальном приближении ^(и) имеет вид:
^(u) =7l"4 + И4= / А (п^г^-^/и)], (2)
f 2 uQ VT “о где k = ^-, X - длина волны, f - расстояние до плоскости фокусировки.
Использование в качестве начального приближения геометрооптической функции ^j(u) обеспечивает быструю сходимость алгоритма. В рассмотренных в п. 3 примерах для сходимости алгоритма требовалось не более 10 иттераций.
С целью улучшения формы фокального распределения интенсивности, в полученном в результате алгоритма Гершберга-Секстона амплитудно-фазовом распределении на апертуре фокусатора wQ1(u)= AQ1(u)exp(i^1(u)) = = An.(u)7(u)exp(iik(u)), где 7(u) = ^‘^^ , амплитудная функция 7(и) не заменяется единицей, а кодируется фа-01 1 А01(и)
зовой функцией. Для фазового кодирования функции у(и) был выбран метод Кирка-Джонса, согласно которому iP](u) примет вид:
ka a q(u) определяется из решения следующего уравнения:
10[Ч(и)]=^. (4)
где 10(х) - функция Бесселя нулевого порядка
С учетом методики расчета, двумерный оптический элемент, синтезированный по вышеописанному алгоритму, может быть отнесен к классу голографических оптических элементов.
Для расчета рассмотренного голографического элемента (1), (3) и оценки поля в фокальной плоскости использовался интеграл Кирхгофа в приближении Френеля. Для характеристики качества фокального изображения используются следующие величины: значение энергетической эффективности -Ей среднеквадратичного отклоне-
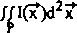
Величина Е =----, _- характеризует долю энергии пучка, попавшую в область фокусировки, где
/Л0(и>12?
G
Р= [-3]; aj х [-а2; а2] - область фокусировки, G = [-Ь; Ь] х [-Ь; Ь] - апертура фокусатора, 1(х) - интенсив ность в фокальной плоскости, I0(u) - интенсивность освещающего пучка.
Величина 5=1 к 1 // [I(x)-l]2d2x]K - характеризует близость распределения интенсивности к посто
I 4аГ2 Р янной величине, где I = ^ * ^ J/I(x)d2 х - среднее значение интенсивности в области фокусировки.
Расчет производился для фокусаторов плоского пучка в квадрат (З] =а2) при следующих физических пара-
, харак-
метрзх: b = 10 мм, X = 10,6 мкм, f = 250 мм, а размер области фокусировки описывался величиной ч теризующей соотношение размера квадрата фокусировки с диаметром дифракционного пятна Д =—.
В таблице приведены значения энергетической эффективности Е и среднеквадратичного отклонения 6 при фокусировке в квадрат для фокусатора 1 - фокусатора с геометрооптической фазовой функцией ^ (и), для фокусатора 2 - фокусатора, полученного по алгоритму Гершберга-Секстона с начальным приближением ^(и) и для голографического элемента (1), (3) в зависимости от величины ч-
Данные таблицы показывают, что при фокусировке в квадрат с размером стороны 23^ » ч голографический элемент по сравнению с конкурентами, обеспечивает лучшую равномерность распределения интенсивности, но обладает более низкой энергетической эффективностью. Однако при фокусировке в квадрат с размерами, близкими к дифракционному, фокусаторы 1, 2 не могут быть признаны работоспособными из-за высокого среднеквадратичного отклонения интенсивности от требуемого распределения.
ч | Фокусатор 1 | Фокусатор 2 | Г ол ографический элемент |
Е (%) | 6 (%) | Е (%) | 8 (%) | Е (%) | 6 (%) |
20 | 913 | 373 | 96,6 | 34,1 | 463 | 313 |
10 | 893 | 453 | 94,2 | 473 | 40,4 | 25,0 |
5 | 84,9 | 56,4 | 95,6 | 433 | 40,7 | 22,4 |
4 | 83,1 | 56,7 | 90,2 | 45 | 37,4 | 34,1 |
3 | 80,4 | 663 | 92,4 | 80 | 24,7 | 31,2 |
2 | 753 | 68,6 | 883 | 573 | 31,0 | 443 |
Среднеквадратичное отклонение для геометрооптического фокусатора 1 при фокусировке в квадрат с размером, меньшим чем 5 т?> составляет более 50%. Дифракционный фокусатор 2 также не позволяет получить достаточно равномерного распределения при фокусировке в квадрат с размером, меньшим чем 41?. Голографический элемент обладает энергетической эффективностью порядка 30% и позволяет сфокусировать излучение в квадрат с размером всего в два дифракционных пятна. Прямоугольная область фокусировки также может быть получена с помощью голограммы с функцией пропускания
T(u, v) = Sinc(ya1u)Sinc(^a(v)exp[- -y(u2 + v2)], (5)
где Sinc(x) = ^‘^Д полученной как результат обратного пересчета поля из области фокусировки на апертуру. Интересно отметить, что голографический элемент при фокусировке в квадрат с длиной стороны 2а. < 5 т? обеспечивает примерно такую же равномерность как и голограмма (5), но обладает существенно более высокой энергетической эффективностью. В частности, при 2а} = 2т? среднеквадратичные отклонения для голограммы и голографического элемента примерно одинаковы — 43% и 443%, однако энергетическая эффективность голограммы всего 5,5%, а энергетическая эффективность голографического элемента - 31%.
Таким образом, голографический элемент является наиболее перспективным среди рассмотренных оптических элементов для случая фокусировки в прямоугольник с размерами порядка нескольких дифракционных пятен. Предложенный подход к синтезу голографического фокусатора в прямоугольник легко обобщается и может быть использован для расчета фокусаторов в произвольную фокальную область.