Исследование и расчет связанных размерных цепей на примере обеспечения показателей точности поворотно-делительных столов
Автор: Бейлин Александр Борисович, Царфин Борис Авдинович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 3 т.22, 2020 года.
Бесплатный доступ
В статье приводятся результаты анализа размерных связей конструкции поворотно-делительного стола, влияющих на показатели геометрической точности. Выявлено, что размерные цепи, описывающие формирование показателей точности, являются связанными. Установлено, что некоторые составляющие звенья размерной цепи меняют свое направление в процессе достижения точности. По результатам расчета разработаны предложения, позволяющие сократить трудоемкость сборки.
Связанные размерные цепи, параметры точности, сборка, компенсатор, поворотный стол
Короткий адрес: https://sciup.org/148314233
IDR: 148314233 | УДК: 621.9 | DOI: 10.37313/1990-5378-2020-22-3-5-11
Текст научной статьи Исследование и расчет связанных размерных цепей на примере обеспечения показателей точности поворотно-делительных столов
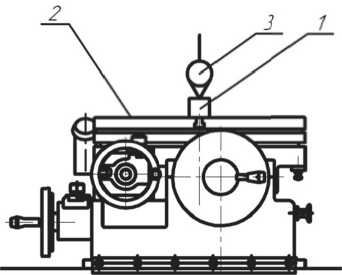
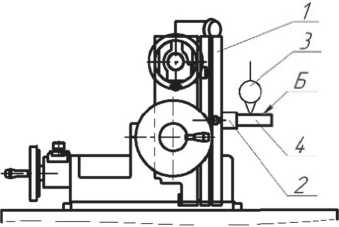
Для расширения технологических возможностей при обработке деталей широко применяют поворотные делительные столы, что позволяет обеспечить высокие требования к точности расположения обрабатываемых поверхностей с многих сторон за один установ заготовки. Обработку деталей можно производить при горизонтальном, вертикальном и наклонном положении планшайбы стола. Универсальные поворотные делительные столы с цифровой индикацией семейства СУ50-1101 (рис. 1) являются прецизионной оснасткой, соответствующей классу точности «С», и могут использоваться при работе в составе координатно-расточных и координатно-шлифовальных станков [1].
Рис. 1. Универсальный поворотный делительный стол
На жёсткой чугунной станине стола 1 установлена люлька 2, имеющая возможность наклона за счёт специальных подшипниковых опор, размещённых в двух ложементах станины. На корпусе люльки смонтировано поворотное устройство, позволяющее обеспечить вращение планшайбы 3 стола.
Параметры геометрической точности стола контролируют на основании программы испытаний, соответствующей требованиям государственного стандарта [2]. Контроль параметров выполняют в соответствии с методами, изложенными в стандарте [3]. Перечень некоторых видов контроля и допустимых отклонений приведен в таблице.
В условиях реального производства изготовление столов со столь жёсткими требованиями к параметрам точности (< 3 ...5 мкм) приводит к значительному количеству неоднократно повторяющихся пригоночных операций, сопровождающихся демонтажом отдельных сборочных единиц и деталей, их доработкой и последующей сборкой, что естественно увеличивает трудоёмкость изготовления. Более того, установлено, что зачастую при доработке одной или нескольких деталей для обеспечения одного параметра точности изменяется другой параметр и его величина становится больше допустимой.
Параметры точности изделия в сборе зависят от точности выполнения размеров деталей и сборочных единиц, влияющих на этот показатель.
Целью данной работы является выявление размерных связей деталей и сборочных единиц поворотного делительного стола, влияющих на величину показателей точности, и разработка рекомендаций, позволяющих снизить трудоемкость сборки.
Таблица 1. Виды контроля геометрической точности стола
|
Контролируемый параметр |
Допустимое отклонение |
|
Прямолинейность рабочей поверхности планшайбы стола |
Т 1 =5 мкм |
|
Торцовое биение рабочей поверхности планшайбы стола |
Т 2 = 5 мкм |
|
Параллельность рабочей поверхности планшайбы основанию стола |
Т з =4 мкм |
|
Параллельность оси наклона планшайбы стола к основанию в вертикальной плоскости |
Т 4 = 3 мкм |
|
Перпендикулярность оси наклона планшайбы к контрольной кромке (пазу) стола в горизонтальной плоскости |
Т ; =3 мкм |
|
Радиальное биение центрирующего цилиндрического отверстия планшайбы стола |
Т б =3 мкм |
МЕТОДИКА ИССЛЕДОВАНИЙ
Методика исследований базируется на теории решения обратных задач размерного анализа. В процессе анализа промежуточных результатов выявлено, что размерные цепи, описывающие формирование показателей точности, являются связанными.
Известны параллельно и последовательно связанные размерные цепи, а также размерные цепи с комбинированной связью [4]. В работах [5, 6, 7] изложены схемы решения линейных параллельно связанных размерных цепей, различающихся по характеру связи. Из множества таких цепей выделяются основные и производные, общее звено которых выступает как составляющее или замыкающее в соответствующих ветвях. В работе [8] отмечено, что данные цепи принадлежат различным уровням конструкторской и технологической сфер реализации функциональных связей. В упомянутых работах не рассматриваются методы решения связанных плоских и пространственных размерных цепей. В руководящем документе [4] дается следующее определение: «Пространственная размерная цепь - размерная цепь, звенья которой расположены в непараллельных плоскостях». В работах [9,10] показано, что пространственную размерную цепь можно рассматривать как состоящую из векторов, модуль и положение в пространстве каждого из них определяются способом задания линейных и угловых размеров в конструкторской документации на соответствующих плоскостях проекций. Таким образом, пространственная размерная цепь формируется последовательностью пространственно расположенных составляющих векторов. Замыкающий вектор связывает конец последнего составляющего вектора с началом первого. Модуль и направление вектора в пространстве могут быть заданы в декартовой, полярной и комбинированной системах координат. Допустимые отклонения параметров в соответствии с возможными способами задания формируют пространственные области допу- стимых отклонений вектора [11]. Методика суммирования составляющих звеньев (векторов), учитывающая области отклонений, позволяет определить координаты номинального положения конца суммарного вектора и предельные области рассеивания суммарной погрешности [10]. Методика расчёта номинального углового положения суммарного вектора в пространстве и его отклонений по осям координат рассмотрены в работе [12].
На рис. 2 показана схема связанных пространственных размерных цепей, имеющих общее звено в качестве составляющего. Решение размерных цепей с общим составляющим звеном не вызывает особых затруднений. Допустимые отклонения на положение и размеры этого звена назначаются обычно из условия экономической целесообразности или функциональных требований, а требуемая точность замыкающего звена в каждой цепи достигается за счет других составляющих звеньев этой цепи или введения компенсаторов.
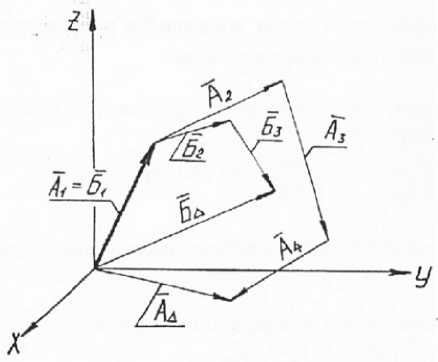
Рис. 2. Связанные пространственные размерные цепи с общим составляющим звеном
Покажем, как формируется составляющий пространственный вектор на примере детали «Ось» (рис. 3), входящей в сборочную единицу «Планшайба».
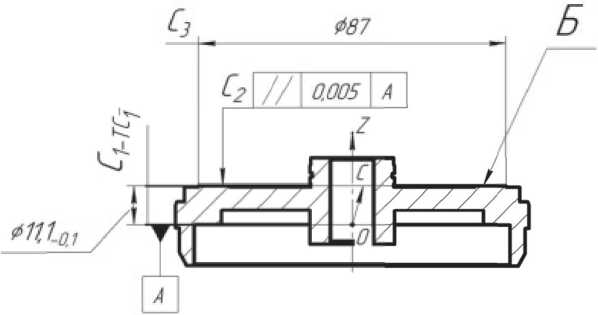
Рис. 3. Ось
Положение поверхности Б относительно базовой поверхности А определяется размером С1=37 мм с допустимым отклонением ТС1= -0,01мм и допустимой величиной отклонения от параллельности ТС2= 0,005 мм. Тогда область Q допустимых пространственных отклонений вектора ОС, связывающего поверхности А и Б, представляет собой шаровой слой толщиной ТС1, вырезанный цилиндром, диаметр основания которого равен диаметру донышка конуса, имеющего длину образующей С1, равную радиусу наружной сферической поверхности. Цен
. 2Т С тральный угол конуса3 = arc tan-—-. Анали тически это можно записать так
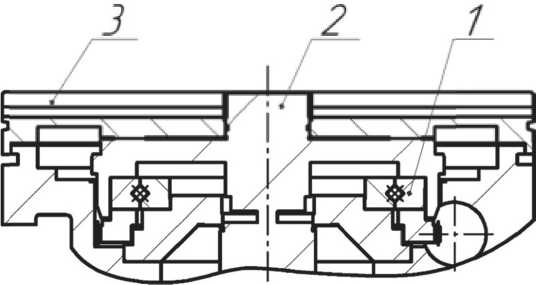
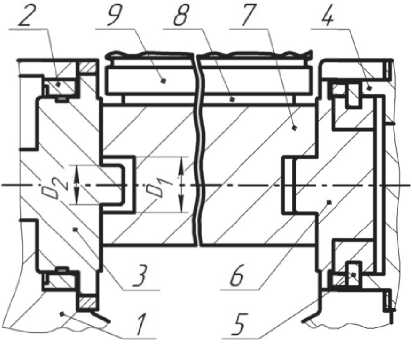
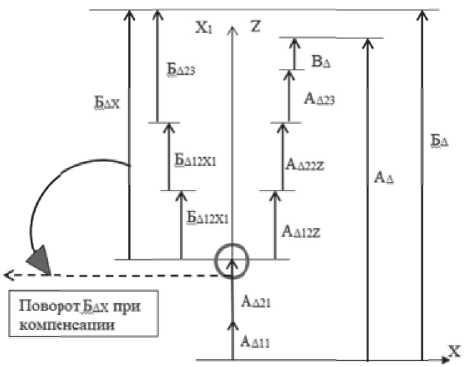
Q = ^х,у,х>.Н^ -x2 -у2 где ^1 — , r7 = C1 - TC , p = C± sin-, x x z. x x 1 x . 2 TC 3 = arc tan . Таким образом, математическое описание, расчёт и анализ областей суммарных погрешностей пространственных размерных цепей является весьма трудоёмкой аналитической задачей. Одним из методов её решения является создание математической модели изучаемого объекта и проведение статистического анализа процесса достижения точности на основе технологии виртуальной сборки с определением величин регулировок компенсаторов [13]. Если все координаты составляющих векторов и их отклонения заданы в декартовых системах координат, причём углы поворота этих систем координат и их отклонения равны нулю, то пространственная область отклонений суммарного (замыкающего) вектора приобретает форму параллелепипеда. Решение задачи размерного анализа такой пространственной размерной цепи сводится к решению трёх независимых линейных цепей. Параметры геометрической точности поворотного стола (табл. 1) контролируются как биения, отклонения от параллельности и перпендикулярности, имеющие, как известно, номинальное значение равное нулю. Поскольку угловые погрешности заданы линейной мерой на контролируемой длине, представим в первом приближении пространственную размерную цепь как линейную. При расчётах методом max-min полученный результат будет получен с избытком и позволит оценить собираемость с применением конструкторского компенсатора погрешностей. Анализ формирования размерных связей, определяющих параметры геометрической точности стола, показал, что они формируются связанными размерными цепями с общими составляющими звеньями. Рассмотрим размерную цепь «В», влияющую на торцовое биение Т2 рабочей поверхности планшайбы стола. Примем следующую систему координат контролируемого стола. Ось Z направлена перпендикулярно основанию стола в сторону планшайбы по оси её вращения. Оси X и Y лежат в плоскости основания стола, причём ось X перпендикулярна оси наклона стола. Контроль торцового биения Т2 выполняют следующим образом. Головку измерительную пружинную 1 устанавливают так (рис. 4), чтобы измерительный наконечник касался проверяемой поверхности планшайбы 2, был перпендикулярен ей и отстоял от оси вращения на расстоянии не менее 200 мм. Проверку биения выполняют плавным поворотом планшайбы стола. За отклонение торцового биения принимают наибольшую алгебраическую разность показаний измерительного прибора. 7 2 Рис. 4. Схема контроля торцового биения планшайбы стола На суммарную величину торцового биения В∆ планшайбы стола (рис. 5) оказывают влияние отклонения геометрических параметров при изготовлении следующих деталей: устройства опорно-поворотного (поз. 1), оси (поз. 2) и планшайбы (поз. 3). Рис. 5. Устройство опорно-поворотное С учётом передаточных отношений ξi составляющих звеньев, характеризующих степень влияния отклонения составляющего звена на отклонение замыкающего звена, размерную цепь запишем в следующем виде: В∆ = ξ1 В1+ξ2 В2+ ξ3В3 +ξ4 В4. Расчёт показал, что В∆=0,0477 мм, то есть В∆ >Т2. Для обеспечения требований ТУ необходимо выполнение пригоночных операций. Рассмотрим размерную цепь «А», влияющую на отклонение от параллельности рабочей поверхности планшайбы основанию стола. Проверку параллельности Т3 выполняют в плоскости параллельной оси наклона планшайбы перемещением стола шагами 50..150 мм (рис. 6). Для этого поверочную линейку 1 устанавливают на поверхности планшайбы 2. Головку измерительную пружинную 3 устанавливают так, чтобы её измерительный наконечник касался рабочей поверхности линейки и был перпендикулярен ей. За отклонение от параллельности рабочей поверхности планшайбы основанию стола принимают алгебраическую разность показаний измерительного прибора в крайних точках перемещения планшайбы. Рис. 6. Проверка параллельности рабочей поверхности планшайбы основанию стола Анализ конструкции стола показал, что в конструкции опоры наклона (рис. 7), монтируемой в широкий ложемент станины, предусмо- Рис. 7. Схема конструкции опор наклона стола: 1 – станина, 2 – кольцо,3 – цапфа, 4 – фланец, 5 – подшипник комбинированный, 6 – цапфа, 7 – корпус, 8 – корпус планшайбы, 9 – планшайба в сборе трен монтажный компенсатор в виде радиального зазора между отверстием в корпусе люльки (D1) и пальцем цапфы (D2). Схема размерной цепи «А» (рис. 8) изображена для компактности как состоящая из промежуточных замыкающих звеньев. Найдем относительное смещение 2*4 .1, оси посадочной поверхности пальца цапфы и оси посадочной поверхности отверстия в корпусе люльки вследствие наличия отклонений при изготовлении деталей. АД = ^Д1 — ^Д2, где ■^д 1 – смещение оси посадочной поверхности пальца цапфы относительно посадочной поверхности узкого ложемента станины; zl л 2 – смещение оси посадочной поверхности отверстия в корпусе люльки относительно той же посадочной поверхности. На суммарную величину смещения ^д 1 оказывают влияние отклонения расположения поверхностей и погрешности размеров при изготовлении станины (А1…А5), кольца (А6) и цапфы (А7). При описании размерных связей деталей, которые поворачиваются при наклоне стола, введем в обозначении звеньев направление оси расчета (Z). Найдём замыкающее звено этого участка размерной цепи, обозначив выражения в скобках как ^дм и АД12г . АД1 = ("А1 + ^2 -^3 + ^4 - |^5 +^б) + = A Здесь 4ш - 0 I I Л — п + °.О15 *Д11 ’ АД12я ~ °-0,015мм. +0,0125 . „+0,0025 -0,0125 мм, АД12г -0,0025 мм. На суммарную величину смещения ^Д 2 оказывают влияние отклонения расположения поверхностей и погрешности размеров при изготовлении фланца (А8…А10), комбинированного подшипника (А11..А13), цапфы (А14..А16), корпуса (А17..А20), корпуса планшайбы (А21) и планшайбы в сборе (В∆). Примем, что торцевое биение планшайбы стола в сборе (В∆) после доработок соответствует ТУ, то есть В∆ ≤ Т2. Найдём замыкающее звено ^Д этого участка размерной цепи с учётом передаточных отношений ξi составляющих звеньев, скомпоновав их с учетом последующих действий. . _ . । । . tn _ „+0,0755 АД2 — АД21 +"A22Z ' АД23 ^22°Д ~ °-0,1200мм, л ^ f а а а Л „ + 0,0025 где 4121 2( А3 А9 ^ю) 0-0,0220мм, лД22г 2 ^112 л122 я132 ' я142 л I л __ д > л + 0,0072 ^152 ' ^16Z ^17z) U-0,0322мм и , _ д । д Ед Ел „ + 0,0598 АД23 - А18'А19 S20A20 S21A21 ~ °-0,0598 мм. Тогда АД = ^Д1 + АД2 = 01J мм. Таким образом А∆ >Т3. Для обеспечения требований ТУ необходима регулировка положения с помощью компенсатора или доработка деталей. Схе- ма размерной цепи «А» (рис. 8) изображена для компактности как состоящая из промежуточных замыкающих звеньев. Рис. 8. Схема связанных размерных цепей стола Рассмотрим размерную цепь «Б», влияющую на отклонение от параллельности оси наклона планшайбы к основанию в вертикальной плоскости. Схема проверки отклонения от параллельности Т4 показана на рис. 9. На планшайбе стола (поз. 1), находящейся в горизонтальном положении, с помощью двух одинаковых по высоте плоскопараллельных концевых мер (поз. 2) устанавливают и закрепляют поверочную линейку (поз. 4) перпендикулярно к контрольной кромке стола и параллельно поверхности планшайбы. Планшайбу поворачивают в вертикальное положение и закрепляют. Головку измерительную (поз. 3) устанавливают так, чтобы её измерительный наконечник касался рабочей поверхности (Б) линейки и был перпендикулярен ей. За отклонение от параллельности оси наклона планшайбы стола к основанию в вертикальной плоскости Т4 принимают алгебраическую разность показаний измерительного прибора на длине измерения (400 мм). Рис. 9. Схема проверки параллельности оси наклона планшайбы стола к основанию в вертикальной плоскости Анализ особенностей конструкции стола выполнен ранее. Найдем относительное смещение Бл оси посадочной поверхности пальца цапфы и оси посадочной поверхности отверстия в корпусе люльки вследствие наличия отклонений при изготовлении деталей. БД = БД1 + БД2, где Б^ — смещение оси посадочной поверхности пальца цапфы относительно посадочной поверхности узкого ложемента станины, а Б^ 2 смещение оси посадочной поверхности отверстия в корпусе люльки относительно той же посадочной поверхности. Введем систему координат X1Y1Z1, жёстко связанную с планшайбой стола, причем координатная ось Y1 совпадает с осью наклона планшайбы. Когда стол находится в горизонтальном положении, то оси X1||X, Y1||Y, Z1||Z. В результате поворота планшайбы в вертикальное положение оси X1Z1 поворачиваются, и ось Z1 становится параллельной оси X, а X1||Z. При проведении размерного анализа конструкции выявлено, что в формировании размерной цепи отклонения от параллельности оси наклона планшайбы стола к основанию в вертикальной плоскости участвует значительное количество размерных связей, влиявших на параллельность рабочей поверхности планшайбы основанию стола. Наименование этих размерных параметров (Ai) оставлено без изменений. При этом некоторые из них остались в неизменном положении и направлены по оси Z, а часть повернулись в связи с наклоном планшайбы. В связи с этим введем в обозначении этих звеньев направление оси расчёта (X1). Смещение Б∆1 оси посадочной поверхности пальца цапфы относительно посадочной поверхности узкого ложемента станины можно найти аналогично смещению А∆1. Выделим в уравнении размерной цепи неподвижные звенья (А∆11), а также звенья, которые повернулись в связи с наклоном планшайбы стола (Б∆12х1). Бм = ("^1 +1^2 - 1^3 + 1^4 - S + S) + + (^^Xl) = А111 + БД12Х1 = 0-0,015мм. — j-iTU.iL1_i_ д Здесь мм, Бд12Х1 ^—0,0025 мм. На суммарную величину смещения Б∆2 оказывают влияние отклонения расположения поверхностей и погрешности размеров при изготовлении фланца (А8…А10), комбинированного подшипника (А11..А13), цапфы (А14..А16), корпуса (А17), корпуса планшайбы (Б1..Б6), опорно-поворотного устройства (Б7..Б10), оси (Б11..Б13) и планшайбы (Б14, Б15). Найдём замыкающее звено Б∆2 этого участка размерной цепи, выделив в уравнении неподвижные звенья (А∆21), а также звенья, которые повернулись в связи с наклоном планшайбы стола ( БД22Х1 И БД23 ): Бд2= >1д21 + Бд22Х1 + Бд23. Q д - j ^п”25 Здесь мм, БД22Х1 ~ 2 ^11X1 ^12X1 -^13X1 + -^14X1 = 15X1 * 16X1 17X1^ -0,0322мм, БД23 = -Б1 + Б2 - Б15 + | (“Б3 + Б4+Б3~Б6- - Б7 - Бв - Б9 + Б10 - Би + Б12 - Б13 - Б14) = 0_02798 мм. мм. Тогда мм. Относительное смещение оси посадочной поверхности пальца цапфы и оси посадочной поверхности отверстия в корпусе люльки со- U R U лл ставляет: Бд Бд1 + Бд2 ^—0,349 мм. Таким образом Б∆ > Т4. Для обеспечения требований ТУ необходима регулировка положения с помощью компенсатора или доработка деталей. Схема размерной цепи «Б» (рис. 8) изобра- жена для компактности как состоящая из промежуточных замыкающих звеньев. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ . Рассмотренные размерные цепи являются связанными. Первой необходимо собирать размерную цепь «В» с обеспечением величины замыкающего звена В∆ ≤ Т2. Предлагается технология упорядоченной сборки, позволяющая путём учёта фактических отклонений сопрягаемых поверхностей деталей (устройство опорно-поворотное + ось + планшайба) и разворота упомянутых деталей в окружном направлении получить в сборочной единице торцевое биение планшайбы близкое к минимально возможному значению для этого комплекта. . Расчет размерной цепи «А» показал, что величина замыкающего звена А∆ > Т3. Однако в конструкции стола имеется конструкторский компенсатор в виде радиального зазора P между отверстием D1=50+0,17 мм в корпусе люльки и пальцем цапфы D2=48-0,17 мм (рис. 7). Отсюда радиальный зазор Р=1+0,17 мм. Поскольку упомянутый зазор больше, чем относительное смещение осей поверхностей сопрягаемых деталей (Р>^), можно утверждать, что технологический процесс сборки с обеспечением отклонения от параллельности по ТУ возможен без доработок с применением регулировок. . Расчет размерной цепи «Б» показал, что величина замыкающего звена Б∆> Т4. На отклонение замыкающего звена Б∆ действуют две группы размерных связей. Первая группа является суммой производственных отклонений А∆11 и А∆21 размеров неподвижных деталей. Эти отклонения компенсируются при сборке размерной цепи «А» в процессе регулировки для обеспечения параллельности рабочей поверхности планшайбы основанию стола требованиям ТУ. Вторая группа является суммой производственных отклонений размеров деталей, которые повернулись в связи с наклоном план- шайбы стола: . „ с „DJD360 _ ' По результатам расчета БДХ — 0,314 мм. Раз мерные цепи «А» и «Б» являются связанными размерными цепями с общими составляющими звеньями (рис. 8). Для обеспечения заданной точности в каждой из этих цепей должен быть предусмотрен свой независимый компенсатор. В конструкции стола предусмотрен только один элемент – зазор между пальцем цапфы и отверстием в корпусе. Однако заметим, что компенсация отклонений А∆ в размерной цепи «А» выполняется в направлении оси Z. Компенсацию отклонений в размерной цепи «Б» нужно выполнять после поворота стола в горизонтальное положение, то есть по оси Х (рис. 10). Z 4 Рис. 10. Схема компенсации погрешностей Располагаемая величина компенсации по оси Х в поле радиального зазора P между отверстием (Д1) в корпусе люльки и пальцем (Д2) цап- фы определяется как Рх = По результатам расчета минимальная вели- чина располагаемого зазора для компенсации по направлению X составляет (Рх)min=0,999 мм. Поскольку (Рх)min>Б∆Х, можно утверждать, что технологический процесс сборки с обеспечени- ем отклонения от параллельности оси наклона планшайбы стола к основанию в вертикальной плоскости по ТУ возможен без доработок с применением регулировок. ВЫВОДЫ 1. На основании проведённых расчётов выявлено, что рассмотренные размерные цепи являются связанными с общими составляющими звеньями. 2. Установлено, что технологические процедуры для достижения параметров точности, соответствующих значениям нормативных до- 3. На основе анализа конструкции стола, существующего технологического процесса сборки и выполненного расчёта размерных цепей разработаны предложения по уточнению процесса сборки, базирующиеся на применении методов упорядоченной сборки и регулировки. 4. Выявлено, что компенсацию отклонений в размерной цепи «Б» для обеспечения параметра точности Т4 нужно выполнять после поворота стола в горизонтальное положение, при этом промежуточные составляющие звенья Б∆х поворачиваются на 90' (рис. 8). 5. Размерные цепи, в которых составляющие звенья меняют свое направление в процессе достижения параметров точности, предлагаем называть «размерные цепи с поворачивающимися звеньями».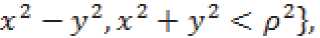

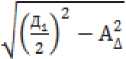
Список литературы Исследование и расчет связанных размерных цепей на примере обеспечения показателей точности поворотно-делительных столов
- Стол универсальный поворотный делительный с цифровой индикацией модель СУ50-1101. URL: http://stan-samara.ru/su_50-11 (дата обращения 12.09.2019).
- ГОСТ 16163-90. Столы поворотные делительные ко-ординатно-расточных и координатно-шлифоваль-ных станков. Основные размеры. Нормы точности.
- ГОСТ 22267-76. Станки металлорежущие. Схемы и способы измерений геометрических параметров.
- РД 50-635-87 Методические указания. Цепи размерные. Основные понятия. Методы расчёта линейных и угловых цепей. Гос. Комитет по стандартизации. М. 1987.
- Балакшин Б.С. Основы технологии машиностроения. М.: Машиностроение, 1969, 385 с.
- Дунаев П.Ф., Леликов О.П. Расчет допусков размеров.-4-изд., перераб. и доп. М.: Машиностроение, 2006. 401с: ил.
- Солонин И.С., Солонин С.И. Расчёт сборочных и технологических размерных цепей. М.: Машиностроение, 1980, 108 с.
- Шевелёв А.С. Структурно-логическая схема обеспечения показателей качества изделий // Изв. высш. учеб. заведений. Сер. «Авиационная техника», 1977. № 1. С. 117-124.
- Дёмин Ф.И. Исследование размерных связей соединений и передач при конструировании и изготовлении изделий // Изв. высш. учеб. заведений. Сер. «Авиационная техника». Казань.1982. №1. С. 77-82.
- Бейлин А.Б., Дёмин Ф.И. Расчёт области суммарной предельной погрешности пространственной размерной цепи // В сб.: «Технологические пути повышения качества изготовления авиадвигателей». Куйбышев: КуАИ, 1986. С. 32-40
- Бейлин А.Б. Предельные области допустимых производственных отклонений размеров деталей // В сб.: «Исследование и оптимальное проектирование станочных систем». Самара: СамГТУ, 1993. С. 45-51.
- Бейлин А.Б. Определение углового пространственного положения стыкуемых плоскостей деталей. Вестник СамГТУ, серия «Технические науки», 2000. Выпуск 10. С. 100-104.
- Чотчаева С.К. Повышение производительности монтажа авиационных агрегатов с использованием их виртуальных компьютерных моделей: автореферат дисс. ... канд. техн. наук: 05.02.08 -Ростов-на-Дону, 2014. 19 с.


