Исследование электромагнитных характеристик кирального метаматериала на основе тонкопроволочных идеально проводящих элементов в виде взаимно ортогональных спиралей

В настоящее время значительный интерес в СВЧ- и оптическом диапазонах представляет исследование различных типов метаматериалов, то есть структур, обладающих нестандартными (для естественных сред) свойствами, возникающими при их взаимодействии с падающим излучением [1]. В СВЧ-диапазоне метаматериалы представляют собой композитные структуры, состоящие из контейнера и размещенных в нем проводящих элементов. Особенный интерес представляют так называемые киральные метаматериалы, создаваемые на основе элементов зеркально асимметричной формы [2]. В роли подобных элементов могут выступать объемные и плоские спирали, S-элементы, гаммадионы, двойные разомкнутые кольца, элементы Тел-леджена и др. На основе киральных структур можно создавать частотно и поляризационноселективные устройства СВЧ, преобразователи поляризации, малоотражающие покрытия, среды с отрицательным преломлением и др.

В 1948 г. Телледжен предположил, что можно создать новый вид материала, основанный на совокупности электрических и магнитных диполей [3]. Простейшим элементом, обладающим указанным свойством, является разомкнутое кольцо с выступающими концами (элемент Телледжена, каноническая спираль). Известны результаты исследования дифракции плоских электромагнитных волн на элементах Телледже-на (С.А. Третьяков, F. Mariotte) [4], цилиндрах с винтовой спиральной проводимостью (Б.З. Каце-неленбаум, А.Д. Шатров и др.) [5], где показано, что в структурах в виде длинных спиралей малого по сравнению с длиной волны радиуса и решеток на их основе наблюдаются поляри-зационно селективные резонансные явления. В [6] подробно изучена возможность использования метаматериалов на основе тонкопроволочных идеально проводящих спиральных элементов для преобразования нормально падающего СВЧ-излучения заданной частоты в рассеяние в плоскости метаматериала.

В предлагаемой работе проведен анализ отражения плоской электромагнитной волны линейной поляризации от планарного слоя метаматериала, созданного на основе двойных взаимноперпендикулярных тонкопроволочных спиральных элементов, а также построена дисперсионная модель такого метаматериала.

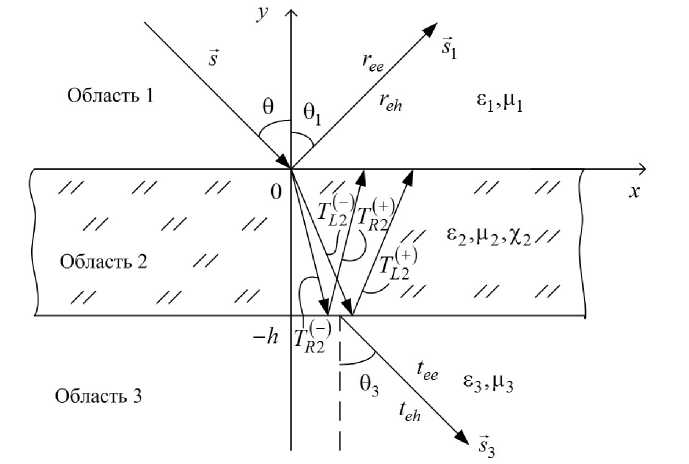
Рис. 1. Геометрия задачи

1. Задача об отражении волны от планарного метаматериала

Рассмотрим задачу об определении коэффициентов отражения и прохождения при падении плоской электромагнитной волны на планарный слой кирального метаматериала, который является бесконечно протяженным вдоль оси Oz . Геометрия задачи приведена на рис. 1. Пусть на киральный метаматериал из полубесконечной диэлектрической области 1 ( ε ₁ и µ ₁ – относительные диэлектрическая и магнитная проницаемости) под углом θ падает плоская электромагнитная волна линейной перпендикулярной поляризации.

Область 2 на рис. 1 представляет собой планарный слой кирального метаматериала толщины h ( ε ₂ и µ ₂ – относительные диэлектрическая и магнитная проницаемости; χ ₂ – относительный параметр киральности). Частотные зависимости материальных параметров ε ₂ и χ ₂ определяются типом резонансных элементов и буду получены в следующем разделе данной статьи.

Киральный метаматериал состоит из двойных взаимноортогональных многовитковых тонкопроволочных спиралей, которые равномерно размещены в планарном контейнере (рис. 2). Совокупность двух взаимноортогональных спиралей будем называть объединенным спиральным элементом. Предполагается, что две спирали в объединенном могут обладать различными геометрическими параметрами и числом витков. В случае киральной среды предполагается, что элементы ориентируются произвольно в кон-

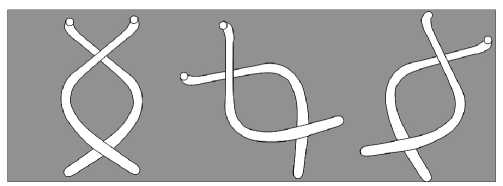
Рис. 2. Геометрия планарного слоя метаматериала тейнере. Объединенные элементы равномерно расположены в контейнере на расстоянии d друг от друга. На рис. 2 для примера показан пример используемого объединенного спирального элемента.

Спирали в объединенном двойном элементе описываются следующими геометрическими параметрами: N_i – число витков; R_i – радиус витка спирали; h_i – шаг спирали; l_i – длина спирали в расправленном состоянии; r_i – радиус проволоки; i = 1,2 – номер спирали в элементе.

Область 3 на рис. 1 представляет собой диэлектрик ( ε ₃ и µ ₃ – относительные диэлектрическая и магнитная проницаемости).

Задача состоит в выводе соотношений для расчета коэффициентов отражения основной (ree ) и кросс-поляризованной (reh) компонент поля в области 1, а также формул для коэффициентов прохождения основной (tee) и кросс-поляризованной (teh) компонент поля в области 3. Здесь уместно отметить, что при взаимодействии падающего СВЧ-излучения с киральной средой всегда возникает явление кросс-поляризации [7; 8], то есть в структуре отраженной и прошедшей волн возникают компоненты поля, ортогональные к компонентам падающей волны. В киральном метаматериале распространяются две волны с право (ПКП) и левокруговыми (ЛКП) поляризациями [2; 7; 8].

Киральный метаматериал 2 описывается материальными уравнениями, одновременно связывающими между собой индукции и напряженности электрического и магнитного полей [2; 7; 8]:

D⁽²⁾ =_S 2 ( to ) E 2 + i X 2 ( to ) H ⁽²⁾, B⁽²⁾ =Ц 2 H ⁽²⁾ ± i X 2 ( to ) E ' ²,

где верхние и нижние знаки соответствует спиральным элементам с право и левовинтовыми закрутками, соответственно. Материальные уравнения (1) записаны в Гауссовой системе единиц.

Электромагнитное поле в киральном метамате- риале определяется из системы двух связанных дифференциальных уравнений 2-го порядка [9]:

V2E(2) + k0 (s2^2 + x2) E(2) - 2гк2№H(2) = 0; V2H(2) + к02 (S2^2 + x2) H(2) + 2ik0s2%2E(2) = 0, где ко = to/c — волновое число для плоской однородной волны в свободном пространстве; to — круговая частота; c – скорость электромагнитной волны в вакууме.

Система уравнений (2) при помощи стандартного представления в виде полей Бельтрами [2; 7]

E ⁽²⁾ = E r + E l ; H ⁽²⁾ = i ^ ( E r - E l ) ,       (3)

сводится к двум однородным уравнениям Гельмгольца для волн ПКП и ЛКП в киральном метаматериале:

• ^V 2 E R , L ± ^kR , L E R , L = ⁰, ⁽⁴⁾ где E r — напряженность электрического поля волны ПКП; E l — напряженность электрического поля волны ЛКП; волновые числа для волн ПКП и ЛКП в безграничной киральной среде определяются следующим образом:

^kR , L (^to) = ^ [V ^e 2 (^to) ^ 2 ± X 2 (^to) ] , ⁽⁵⁾

Из решения уравнений (4) с использованием представлений (3) для продольных составляющих векторов поля в киральном метаматериале получаются следующие выражения [9]:

g ⁽²⁾ _ jUg- ^ik R ^{( 5} r , ^{r )} ₊ E^e ^ik R ⁽® R ,r) +

+^_е - ^ TL + w      ,6,

g ^(-)_e- ^ik R ⁽ S r , r ) ₊ J'Wg ^ik R ⁽ S r ,I) _

• - T;. - ik L« L . r ) ; t_w •

  H (2) = 1- z

  П 2

  
  

где sR,L = {sin 9r,l , - cos 6r,l }   — единичные вектора, вдоль которых распространяют- ся преломленные волны в метаматериале 2;

I ( + , L = { ^{sin 9} R , L ,^{cos 9} R , L }

–

единичные векто-

ра, вдоль которых распространяются волны, отраженные от области 3; 9 r l — углы преломления волн ПКП и ЛКП, соответственно; П^{( 2 )} = VЦ 2 /^е2 — характеристическое сопротивление кирального метаматериала; rR /^ и tL^-^ — коэффициенты прохождения (по полю) волн ПКП и ЛКП в метаматериал 2; tR⁺^ и R + — коэффициенты отражения (по полю) волн ПКП и ЛКП от области 3 в киральный слой.

Явные выражения для всех тангенциальных ( 2 )         ( 2 )

составляющих векторов E и H в киральной среде приведены в [9].

Для случая падения плоской электромагнит- ной волны с перпендикулярной поляризацией для составляющих поля в диэлектрической области 1 справедливы следующие выражения, записанные с учетом кросс-поляризации:

E Z ¹ = _e ^- ik i ⁽ s , r ) ₊ r ee e ^- ik i ⁽ s r , r ) ;

• (1)    _ cos ⁹ ik i (s , r )        cos 9 ik i ( ^s r , r )

x           ( 1 ) e             ⁺ r ee ( 1 ) e             ;

H Z ¹) = r eh e ^{- ik1 ( s} r , ^{r )};

EX1 =-rehП(1) cos 9e-iki(rr,r), где sr = {sin 9,cos 9} — единичный вектор, определяющий направление распространения отраженной волны в области 1; ree – коэффициент отражения (по полю) основной компоненты; reh – коэффициент отражения (по полю) кросс-поляризованной компоненты; ki = ко ^ Б1Ц1 — волновое число для плоской однородной волны в области 1. При решении задачи предполагается, что на киральный слой падает волна с единич- ной амплитудой напряженности электрического поля; n(1) = VЦ1 /е1 — характеристическое сопро- тивление области 1

Для составляющих векторов электромагнитного поля в области 3 с учетом кросс-поляризации можно записать следующие выражения:

(3)=t е- ikз(sз,r)• z       ee e;

hZ³⁾ = t eh e ^{- ik} 3 ^{( r} 3 ’ ^r ) ;

EX3)= tehП(3) cos 9з e-ik3(S3’S);

H(3)=-1 cos 93 e-ik3(S3’r)• x ee (3) e;

где s3 = {sin 93, - cos 93 } — единичный вектор, определяющий направление распространения прошедшей волны в области 3; tee – коэффи- циент прохождения (по полю) основной ком- поненты; teh – коэффициент прохождения

(по полю) кросс-поляризованной компоненты;

n^{( 3 )} = V Цз Аз

характеристическое сопротив- ление области 3; кз = ко^£3^3 — волновое число для плоской однородной волны в области 3.

На последнем этапе решения задачи исполь- зуются граничные условия для тангенциальных составляющих векторов напряженностей электрического имагнитного полей на границах раздела при у = 0 и y = -h:

Е1) (у = 0) = Е® (у = 0);

H T ¹ ) ( у = 0 ) = H T ¹ ) ( у = 0 ) ;

М 2) ( у = - h ) = Е < ³⁾ ( у = - h ) ;

H < ²⁾ ( у = - h ) = H T ³⁾ ( у = - h ) .

В результате подстановки выражений (6), (7) и (8) в граничные условия (9) относительно неизвестных коэффициентов отражения и прохождения получаем неоднородную систему линейных алгебраических уравнений (СЛАУ) вида: ^*  —*      —*

AT = P ,                                  (10)

где A — квадратная матрица размером 8 х 8, явный вид элементов которой в статье не приводится в силу их громоздкости; ^—

T=

= [ Г ее r eh T R T^ T ? T L - t ee t eh ^] ;

P = [ 0 - 1 cos 0 1 /n⁽¹⁾ 00000 ] .

Коэффициенты матрицы Л определяются геометрическими параметрами контейнера и объединенных спиральных элементов; материальными параметрами кирального метаматериала и областей 1 и 3.

Аналогичным образом рассматривается случай падения волны с параллельной поляризацией и решение задачи сводится к СЛАУ (10) с другими коэффициентами матрицы Л и вектор-столбцом P ^— .

2.    Дисперсионная модель метаматериала на основе объединенных спиральных элементов

Рассмотрим киральный метаматериал на основе объединенных спиральных элементов (рис. 3). Каждый из двух подэлементов объединенного элемента представляет собой тонкопроволочную проводящую спираль, состоящую из N витков.

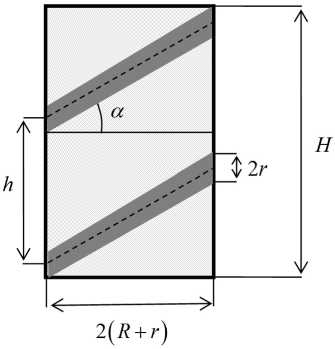
Рис. 3. Поперечное сечение одной спирали из объединенного элемента

Обозначим: N_i – число витков; R_i – радиус витка спирали; h_i – шаг спирали; l_i – длина спирали в расправленном состоянии; r_i – радиус проволоки; a i — угол накрутки спирали.

Для расчета резонансной частоты объединенного элемента воспользуемся формулой Томсона:

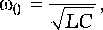
где L – индуктивность объединенного элемента;

C – емкость объединенного элемента.

Индуктивность и емкость объединенного элемента определяются через соответствующие характеристики одиночных спиралей следующим образом:

C = C 1 + C 2 ; L = -LL -,                (12)

L 1 ⁺ L 2

где L_i – индуктивность одной из спиралей; C_i – емкость одной из спиралей ( i = 1,2).

Емкость одной спирали определяется следующим образом:

г прр i ⁺ м»в i ⁺ ммз i ,

то есть в виде суммы емкости проволоки, меж-витковой емкости и межэлементной емкости и в итоге выражается следующим образом:

C i = ^£ с 2

---->---10^-11 +

18lnI 2l^\-1

I ri J

пГ(Ri + 2r)2 - Ri2 ](Ni -1) + —---------------+ hi

1 N i ( R i + r )

+--------------- ri d cos ai

Индуктивность одной спирали вычисляется по формуле:

L i = Ц c 2

n N_i² R_i ^^ l_i

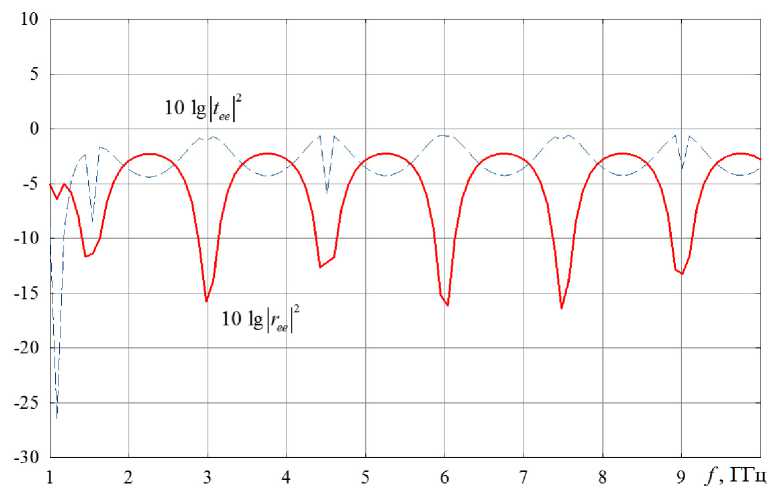
Рис. 4. Частотные зависимости прошедшей и отраженной мощностей для случая идентичных спиралей в объединенном элементе

В формулах (14) и (15) б c 2 , ц c 2 — относительные диэлектрическая и магнитная проницаемости контейнера.

Подставляя соотношения (14), (15) в (12), а затем в (11) получаем формулу для резонансной частоты объединенного элемента.

Дисперсия диэлектрической проницаемости и параметра киральности определяются следующими выражениями [10]:

^Б 2 ( to ) - Б c 2 +

в2     .

;

to0 -to

Х 2 (^to) ^{- Д} 0

P(0to c (to0 -to2),

где Д и во — параметры, определяемые размерами объединенных элементов и расстоянием между ними, соответственно.

Подставляя в формулы (16) выражение для резонансной частоты объединенного элемента (11), получаем дисперсионные соотношения для диэлектрической проницаемости и относитель- ного параметра киральности метаматериала на основе тонкопроволочных идеально проводящих элементов в виде взаимно ортогональных спиралей.

3.    Численные результаты

При анализе численных характеристик основной интерес представлял расчет частотных зависимостей отраженной (10 lg r_ee ² и 10 lg r_eh ²) и прошедшей (10 lg t_ee и 10 lg t_eh ) мощностей

(в дБ). Контейнер моделировался на основе пенополистирола С-35 с относительной диэлектрической проницаемостью б _c 2 - 1.5.

На рис. 4 представлены частотные зависимости отраженной и прошедшей мощностей основной и кросс-поляризованной компонент поля в диапазоне от 1 до 10 ГГц. Штриховыми кривыми на рис. 4 показаны зависимости прошедшей мощности основной компоненты (10 lg t_ee ²); сплошными линиями – отраженной мощности основной компоненты (10 lg r_ee ²). Падение волны на метаструктуру считалось нормальным. Расчет был выполнен при следующих значениях параметров структуры: R 1 2 - 0.01 м, N 1 2 - 3, r 1,₂ - 0.002 м, H 1,₂ - 0.05 м, d 1,₂ - 0.05 м. В этом случае обе спирали, входящие в структуру объединенного элемента, являются тождественными.

Уровень отражения и прохождения кросспо-ляризованных компонент поля не превышает при нормально падении –25 дБ и на графиках не представлен.

На частоте 1.18 ГГц наблюдается резкое локальное уменьшение уровня прошедшей мощность через исследуемый метаматериал, то есть преимущественно происходит боковое рассеяние нормально падающей электромагнитной энергии. На этой частоте метаструктура может выполнять роль частотно селективного защитного экрана. На других частотах метаструктура является полностью прозрачной и падающее излучение через нее проходит практически без ослабления (вблизи 0 дБ).

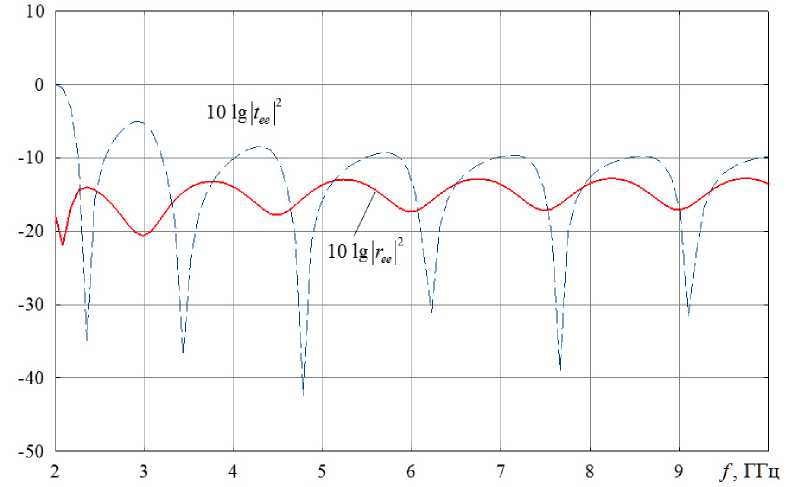
Рис. 5. Частотные зависимости прошедшей и отраженной мощностей для случая неидентичных спиралей в объединенном

элементе

Можно отметить, что исследуемая метаструктура на одной частоте может выполнять роль частотно-селективного защитного экрана, не прозрачного для излучения вблизи основной резонансной частоты.

Рассмотрим теперь случай различных по значениям геометрических параметров спиралей в структуре объединенного элемента.

На рис. 5 представлены частотные зависимости отраженной и прошедшей мощностей основной и кросс-поляризованной компонент поля в диапазоне от 1 до 10 ГГц. Штриховыми кривыми на рис. 4 показаны зависимости прошедшей мощности основной компоненты (10 lg t_ee ²); сплошными линиями – отраженной мощности основной компоненты (10 lg r_ee ²). Падение волны на метаструктуру считалось нормальным. Расчет был выполнен при следующих значениях параметров структуры: R i = 2 R 2 = 0.01 м, N 1,₂ = 3, r 1 = 2 r ₂ = 0.002 м, H 1 = 2 H ₂ = 0.05 м, d 1 = 2 d 2 = 0.05 м.

Как видно из рис. 5, в случае несимметричного двойного спирального элемента возникает резкая частотная селективность прохождения электромагнитного излучения через метаматериал. В отличие от симметричного двойного спирального элемента здесь возникает сильная киральность и, как следствие, возникает набор дискретных частот, на которых электромагнитная волна через метаматериал не проходит и преобразуется в боковое рассеяние. Также можно отметить, что в этом случае отражение и прохождение кросс поляризованных компонент поля так же возрастает до –15–18 дБ. Кроме того, отсутствуют частоты, начиная с 2 ГГц, на которых уровень ослабления прохождения основной компоненты поля близок 0 дБ, что связано с ростом кросс поляризации. На резонансных частотах структура может играть роль защитного экрана СВЧ.

Также было доказано, что исследуемая метаструктура по свойствам является эквивалентной естественному кристаллу (или искусственной брэгговской решетке) в оптическом диапазоне, а именно частоты резонансных минимумов ослабления прошедшей мощности основной компоненты поля вычисляются из условия Вульфа-Брэгга с учетом преломления электронных волн в кристалле [11]:

^{2 d} ^( ^s 2 ^ 2 -^х 2 ) - cos² 6 = ^vX , ⁽¹⁷⁾ где V — порядок резонанса; X - длина волны; 0 - угол падения волны.

Заключение

Таким образом, по результатам работы можно сделать следующие выводы:

• 1.    Наличие двух идентичных тонкопроволочных спиралей в объединенном элементе сводит эффект киральности и, как следствие, частотной селективности всего метаматериала практически до нуля.

• 2.    Наличие двух различных по геометрическим размерам спиралей в объединенном эле-

• менте увеличивает степень киральности всего метаматериала в целом и возникают частотная селективность прохождения плоской электромагнитной волны через метаматериал и достаточно большая кросс-поляризация поля.

• 3.    Исследуемая метаструктура в случае различных спиралей в объединенном элементе по свойствам является эквивалентной естественному кристаллу (или искусственной брэгговской решетке) в оптическом диапазоне.

• 4.    Метаструктура в случае различных спиралей в объединенном элементе может выполнять роль частотно селективного защитного экрана СВЧ.