Исследование электромагнитных характеристик планарных киральных метаструктур на основе составных спиральных компонентов с учетом гетерогенной модели Бруггемана

В настоящее время значительный интерес представляет исследование электродинамических свойств метаматериалов СВЧ-диапазона, которые представляют собой композиционные искусственные структуры, обладающие ярко выраженными частотно-селективными свойствами [1–3]. Уникальные свойства метаматериалов обусловлены как их пространственной структурой, так и свойствами компонентов (микрочастиц), из которых они состоят. Практически любой метаматериал представляет собой композицию контейнера из материала со свойствами А, в котором каким-либо образом размещены компоненты со свойствами Б. Компоненты Б могут размещаться как упорядоченно, так и смешиваться с несущим материалом А. Одним из перспективных классов метаструктур является киральный метаматериал (КММ), который создается из компонент Б, обладающих зеркально асимметричной пространственной конфигурацией [4-6]. Исследование указанных сред, называемых киральными, активно

началось в конце XX века, когда были определены их основные электромагнитные свойства, такие как кросс-поляризация, частотная и поляризационная селективность и т. п. [5–7]. Новый скачок в развитии киральных метаматериалов наступил в начале XX века, когда активно заговорили о возможности создания сред с отрицательным преломлением (сред Веселаго) [8; 9], в которых зачастую использовались компоненты с зеркально-асимметричной пространственной конфигурацией. В настоящее время основными трендами развития электродинамики метаматериалов являются построение математически корректных математических моделей КММ; расширение полосы частот, в которой метаматериал проявляет требуемые свойства; исследование управляемых полем (смарт) метаматериалов; создание метаповерхностей и т. п. [3].

Используемые в настоящее время математические модели КММ в большинстве случаев являются недостаточно общими, так как не учитывают всех основных свойств метаматериалов.

В частности, до сих пор мало обсуждается вопрос о том, чем вызваны уникальные свойства кираль-ных метаматериалов – пространственным размещением компонентов Б в несущей среде А или же пространственной конфигурацией используемых зеркально-асимметричных компонент Б. В материальных уравнениях для киральной среды в формализме Линделла – Сиволы [4] и в других формах записи материальные параметры являются эффективными, но при этом в них отсутствует явная зависимость от материальных параметров среды А и компонентов Б.

Благодаря преобразованиям микро- или макроструктуры у искусственного материала в целом изменяются его электрофизические свойства (диэлектрическая и магнитная проницаемости) и, как следствие, проявляются электромагнитные свойства, которые не присущи естественным материалам природного происхождения.

Преобразование макроструктуры вследствие помещения компонентов Б в контейнер А позволяет характеризовать метаматериал как гетерогенную среду.

В предлагаемой статье будет построена математическая модель КММ, в которой будут учтены основные физические и геометрические свойства кирального метаматериала – киральность, гетерогенность и дисперсия.

Гетерогенность . Упорядоченное размещение микроэлементов в контейнере. Для описания данного свойства в работе использовалась модель Бруггемана [10; 11].

Киральность . Микроэлементы имеют зеркально-асимметричную форму. Для описания данного свойства использовались материальные уравнения в формализме Линделла – Сиволы.

Дисперсия . Зависимость материальных параметров метаматериала от частоты. Для этого использовалась модель Кондона, известная из квантовой теории оптически активных сред.

Таким образом, в статье будут записаны материальные уравнения для обобщенной киральной среды, учитывающие все указанные физические и геометрические свойства как компонентов Б, так и несущей среды А.

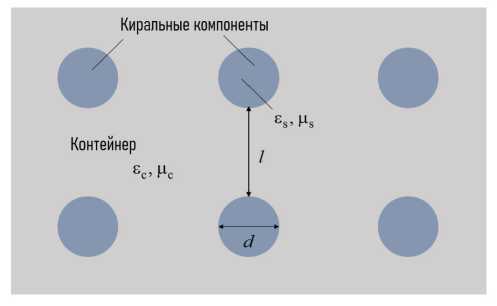
Рис. 1. Общая структура кирального метаматериала

Fig. 1. General structure of a chiral metamaterial нове компонентов как минимум двух типов, хотя бы один из которых обладает свойством зеркально асимметрии. В рамках данной статье будем предполагать, что в несущем контейнере А размещаются зеркальные компоненты одного типа Б, которые являются тождественными.

Обычно киральная метаструктура представляет собой совокупность однородного диэлектрического контейнера (несущая среда А) с относительной диэлектрической проницаемостью s c и относительной магнитной проницаемостью ц_с, в котором размещаются зеркально-асимметричные компоненты Б. Они равномерно размещаются и хаотически ориентируются в диэлектрическом контейнере. Расстояние между соседними компонентами обозначим через l ; размер области, занятой одним киральным компонентом – через d . По сути, КММ представляет собой совокупность несущей среды, в которую помещена матрица из киральных компонентов Б с периодом решетки l .

Общая структура кирального метаматериала приведена на рис. 1.

Киральные компоненты представляют собой микроскопические электромагнитные частицы, соизмеримые с длиной волны СВЧ-поля, и являются переизлучателями электромагнитного поля (ЭМП). Зеркально-асимметричные элементы проводящие.

КММ представляет собой совокупность несущей среды (контейнера) и зеркально-асимметричных компонентов, поэтому для его описания в целом вводятся эффективные диэлектрическая и магнитная проницаемости, которые зависят от соответствующих проницаемостей контейнера и киральных элементов:

^e = ^e ( ^e c > ^s s ) ; Ц = ц ( ^ с > ^ s ) • ⁽¹⁾

Таким образом, любой киральный метаматериал описывается набором из трех материальных параметров (1) – эффективными диэлектрической проницаемостью g, эффективной магнитной проницаемостью ц и параметром киральности X-

Материальные уравнения для киральной среды, согласно формализму Линделла – Сиволы, имеют следующий вид:

—* —* —* —* —* —*

D = g E + i X н , в = Ц н ± i X E . (2)

В соотношениях (2) верхние знаки соответствуют КММ на основе зеркально-асимметричных компонентов с правой закруткой (правых форм компонентов), а нижние знаки – КММ на основе зеркально-асимметричных компонентов с левой закруткой (левых форм компонентов).

Подставляя в материальные уравнения (2) формулу для эффективной диэлектрической проницаемости по модели Бруггемана (6), получаем:

f

' ^gsU ^{3 а} ) ^g c ( ^{2 3 а} ) ]

I +^g c ^g s

-

^[g s ( ^{1 - 3 a} ) ^-g c ( ^{2 - 3 а} ) ]

> E ( г ) + i X н ( Г ) ;          (7)

1.1. Учет гетерогенности КММ. Для описания пространственной структуры метаматериала воспользуемся моделью (формулой) Бруггемана [10; 11]:

^{( 1 -а)}

^g c ^-g g c + 2g

+ а

-g

g s + 2g

= 0,

— — — в (г ) = ц н (г )± i X E (Г).

Соотношения (7) определяют математическую модель однородного кирального метаматериала с учетом свойства гетерогенности.

Кроме учета свойства гетерогенности кираль-ного метаматериала необходимо учесть и свойство дисперсии материальных параметров. Для этого воспользуемся моделью Кондона.

где g - относительная эффективная диэлектрическая проницаемость КММ (как пространственной структуры, состоящей из несущей среды А и компонентов Б); g c - относительная диэлектрическая проницаемость несущей среды А; g_s - относительная диэлектрическая проницаемость области, занятой компонентом Б; а - объемная концентрация компонент Б.

Из формулы (3) можно получить выражение для эффективной диэлектрической проницаемости КММ:

1.2. Учет дисперсии КММ. Киральный метаматериал обладает пространственной дисперсией, как следствие, его диэлектрическая проницаемость и параметр киральности зависят от частоты падающего ЭМП. В научной литературе доказывается, что в случае кирального метаматериала (по аналогии с оптически активной средой в оптике) частотные зависимости диэлектрической проницаемости и параметра киральности определяются формулой Кондона [12]:

^g s ( ® ) = ^g c

П „ Hi ^g (n i ,П ) = ^ — ^- П ^- у,

-BL ;

2     2

to Q -to

% ( © ) =

A в2 to c (toQ - to2

где

П 1 =

^[g s ^{( 1 - 3 a)-g} c ⁽ 2 ^{- 3 а)} ]          ^g_c^g_s

-----------2----------- ^{; П} 2 = " If".

Подставляя выражения (5) в решение (4), полу-

чаем для эффективной диэлектрической прони-

цаемости в модели Бруггемана следующее соот-

ношение:

_ ^[g s ^{( 1 - 3 a)-g} c ⁽ 2 ^{- 3 а)} ]    g c g s

=11         16         + т -          (6)

^[g s ( ^{1 - 3 a} ) ^-g c ( ^{2 - 3 а} ) ]

.

Соотношения (7) определяют (согласно модели Бруггемана) эффективную диэлектрическую проницаемость метаматериала через относительные диэлектрические проницаемости контейнера А и области, занятой компонентами Б.

где g_" - относительная диэлектрическая проницаемость области, занятой киральным компонентом Б; а - объемная концентрация компонента в контейнере А; X - параметр киральности КММ; c – скорость электромагнитной волны в вакууме; A – параметр, имеющий размерность длины и связанный с расстоянием между элементами; P q - параметр, имеющий размерность частоты и связанный с внутренними процессами в среде.

Резонансная частота to Q определяется формой и размерами кирального компонента. Для КММ на основе различных зеркально-асимметричных компонентов расчет резонансной частоты производится по-разному и определяется пространственной формой компонента.

Поставляя формулу (8) в материальные уравнения (7), получаем математическую модель кираль-ного метаматериала, учитывающую свойства ки-ральности, гетерогенности и дисперсии:

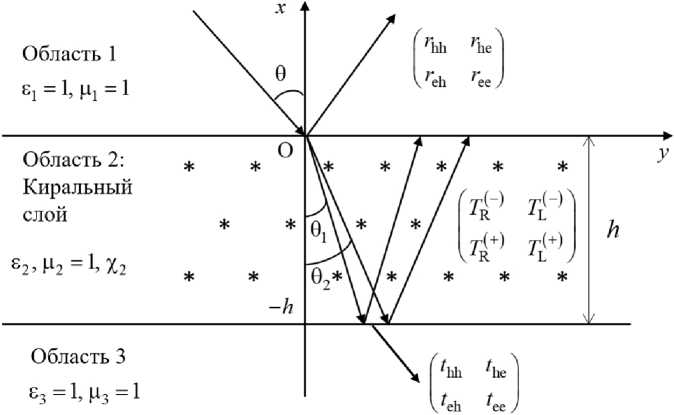
Рис. 2. Геометрия задачи

Fig. 2. Problem geometry

ID ( to ) = s ( to ) E ( to ) + i „³0 H ( to ) ; c ( to 0 -to ² )

-         „          A P o ^to „

B | Л il H ^(to) ± i— E ^(to) ;

c I to 0 -to ² )

к ^{( 1 - 3 a)-e} c ⁽ 2 ^{- 3 a)} ] + S c S s 16               2

дН 3a) Л Л

в слое КММ равна « 2 . Толщина планарного слоя КММ h . Область 3 является диэлектриком с диэлектрической и магнитной проницаемостями б ₃ и ц ₃ . При решении задачи также предполагается, что на всех границах раздела отсутствуют поверхностные заряды и токи. Также будем считать, что КММ является неограниченно протяженным вдоль оси Oz . При решении задачи будем учитывать явление кросс-поляризации, возникающее при отражении (прохождении) электромагнитной волны от слоя из кирального

eO

^S s ^(to) = ^e s ⁺ "1----2

to o -to

2. Использование построенной модели КММ для решения задачи об отражении (прохождении) плоской электромагнитной волны от планарного слоя КММ

Рассмотрим задачу о падении плоской электромагнитной волны линейной (E- или H-поляризации) на планарный слой из кирально-го метаматериала. Геометрия задачи приведена на рис. 2.

Плоская электромагнитная волна падает на планарный слой КММ под углом 9. Область 1 на рис. 2 является диэлектриком с диэлектрической и магнитной проницаемостями s 1 и ц 1 . Слой КММ (область 2) описывается материальными параметрами: S 2 , Ц 2 и Х 2 в рамках построенной математической модели (9). Объемная концентрация зеркально-асимметричных компонентов

метаматериала, а именно, при падении волны с E-поляризацией будут возникать компоненты отраженного и прошедшего ЭМП с H-поляризацией и обратно.

Коэффициенты отражения плоской волны от слоя КММ определяются следующей матрицей:

U . г. D

' hh ' he '== ^ eh ee у

где r _hh – коэффициент отражения ЭМП с H-поляризацией при падении ЭМП с H-поляризацией; r _he – коэффициент отражения ЭМП с H-поляризацией при падении ЭМП с E-поляризацией; r _ee – коэффициент отражения ЭМП с E-поляризацией при падении ЭМП с E-поляризацией; r eh - коэффициент отражения ЭМП с E-поляризацией при падении ЭМП с H-поляризацией.

По аналогии коэффициенты прохождения в области 3 могут быть упакованы в матрицу коэффи-

циентов прохождения, где смысл индексов аналогичен (9):

T =

thh   the vteh   teeу

.

Внутри слоя из кирального метаматериала будут распространяться волны с право- (ПКП) и левокруговыми (ЛКП) поляризациями - две преломленные из области 1 и 2, отраженные от границы раздела с областью 3. Для их описания можно ввести матрицу коэффициентов отражения-прохождения волн ПКП и ЛКП в области 2:

S =

t R ) т ( ) . t R +) T ^ .

Таким образом, требуется определить матрицы коэффициентов отражения и прохождения основной и кросс-поляризованной компонент поля (10)–(12).

При решении задачи воспользуемся методом частичных областей с учетом киральности среды, представленным в [13].

Планарный слой КММ описывается следующи- пряженность электрического поля волны с левой круговой поляризацией.

В формуле (16):

^k R,L = k 0 [V^e 2 ( ^ю ) - 2 ± Х 2 ( ^ю ) ]                        ⁽¹⁷⁾

- волновые числа для волн ПКП и ЛКП в неограниченной киральной среде [4; 5].

Решения уравнений (16) являются известными и представляют собой совокупность двух волн, прошедших в киральный метаматериал, и двух волн, отраженных обратно в слой метаматериала от границы раздела с областью 3 [12]:

E ^{( 2 )} = T ⁽-) e - ik R ⁽ s R , ^r ) + T ^{( +} )e - ^R^R > r ) +

+ T We ik l ^{( s} l > s ) ₊ t (+) e ik l ^{( s} l , r ) .

H ¹²

i t ^{( - )} e ik r ⁽ ® r , r ) ₊ t ^{( + )} e ^ik R ⁽ S R , f ) _ П 2 L

ми материальными уравнениями:

D ⁽²⁾ = б ₂ ( ю ) E ⁽²⁾ + i х ₂ ( ю ) H ⁽²⁾ ;

B ⁽²) = _Ц 2 H ⁽²⁾ ± i Х 2 ( ю ) E (²⁾ ,

T( ~)e^{_ ik} L⁽ s L > r ) _ T (^ + )e— ^ik L ^{( S} + > ^? )

^•-

где s

i R,L = { ^_ cos ⁶ R,L ,s ^{in 6}R,l }

–

единичные век-

где верхние и нижние знаки определяют правую или левую форму зеркально-асимметричных компонентов. Соотношения (13) записаны в Гауссовой системе единиц. При этом используется построенная математическая модель (9)

Векторы напряженностей электрического и магнитного полей в слое из кирального метаматериала находятся из следующих дифференциальных уравнений [13]:

V 2 E ⁽²) + к ² [б 2 ( ю )^ +х 2 ( ю ) ] E ⁽²⁾ -

торы, вдоль которых распространяются волны, прошедшие в область 2 из области 1; s R l = = { cos0 RL ,sin 6 rl } — единичные векторы, вдоль которых распространяются волны, отраженные

от области 3 в область 2; 9 rl — углы преломления волн ПКП и ЛКП соответственно; п = д/-2/ ^е 2

–

импеданс (характеристическое сопротивление)

кирального метаматериала; k R l = к 0 ( n 2 ± Х 2 )

–

постоянные распространения нормальных волн ПКП и ЛКП в киральном слое; n 2 = ^ Б 2 Ц 2 — относительный показатель преломления для области 2.

- 2i к ² Ц 2 х ₂ ( ю ) H ⁽²⁾ = 0;

^{Х Н (2)} + k ² [₆ 2 ( ^ю ) ц 2 +Х 2 ( ^ю ) ] ^{H (2)} +

В статье были рассмотрены случаи ЭМП с E-поляризацией:

E ( 1 ) = e -i ^k 1 ( ^s ind ^{, s} ) ₊ r_££ e -i ^k 1 ( f ) .

падения

+ 2i к0Б2 (ю)х2 (ю) E(2) = 0, где k0 – волновое число для плоской однородной волны в вакууме.

Векторы напряженностей электрического и магнитного полей в слое из кирального метаматериала представляются в виде суперпозиции полей волн с круговыми поляризациями (полей Бельтрами):

E ⁽²⁾ = E r + E l; H ⁽²⁾ = i^f 2 -M( E r - E l ) ,       (15)

в результате чего получаются однородные уравнения Гельмгольца для волн ПКП и ЛКП:

^V 2 ^E R,L ± ^k R,L ^E R,L = ⁰ , (16) где E r - напряженность электрического поля волны c правой круговой поляризацией; E l - на-

( 1 ) ₌COS0 ^{- i} k 1 ( s ind . r )_     COS0 ^{- i k} 1 ( S r_ef , r )_

H y           ^e                ' ee ^{e            ;}

y     ⁿ 1                      ⁿ 1                      (19)

h ( .)= r eh e -i k ¹ ( s re, . r ) .

E(1) = rehn cos6 e ik1(sref’r), и H-поляризацией:

H ( 1 ) = _e -i ^k 1 ( ^s ind > ^s ) ₊ „ _{L e} -i ^k 1 ( ^s ref . r ) .

z                   hh

E y ^ = -П 1 cos 6 e i k ^{1 (} s ^ind’ ^r ) + r hh cos6 e i k ^{1 (} s ref ’ r ) ;

_E ( 1 )-, _e- i ^k 1 ( ^S ref ^{, S} )                                           ⁽²⁰⁾

E z = ^r he ^e            .

H ( 1 ) =-    COS ⁶ e^{- i k} 1 ^{( S} r_ef , ^r ) .

^y e П 1

В соотношениях (19)-(20): k1 = к0^Б1-1 - волновое число для плоской однородной волны в области 1; sref = {cos 9, sin9} - единичный вектор, определяющий направление распространения падающей волны; г = {x, у} - радиус-вектор точки

наблюдения; гц = JЦ1 /е1 — характеристи- ческое сопротивление (импеданс) диэлектрической области 1; s^ = {-cos9, sin9} - единичный вектор, определяющий направление распространения падающей волны.

Поле в области 3 находится по аналогии [13].

На границах раздела выполняются граничные условия для тангенциальных составляющих векторов напряженностей электрического и магнит- ного полей [14]:

E Т¹) ( у — 0 ) = E <²⁾ ( у — 0 ) ;

H Т¹) ( у — 0 ) = H Т¹) ( у — 0 ) ;

E <²⁾ ( у = - h ) — E Т3) ( у = - h ) ; н Т²⁾ ( у —- h ) = h <3 ’ ( у —- h ) .

После подстановки соотношений (18), (19) и (20) в граничные условия (21) получаем неоднородную систему линейных алгебраических уравнений следующего вида, например, для случая падения ЭМП H- и E-поляризации:

—*             —*

B H,E R H,E = A H,E .

r  — Г t ( ^{- )} , t <+> , t( -

E I R R L

T L+’, r ee , r eh , t ee , t eh ] ;

—

A E =

-iT

1,0,0,—, 0,0,0,0

П1           ]

;

r Г т^{( - )} t^{( + )} t^{( - )} t^{( +} )                    1 •

^K H ^— [ T R , T R , T L , T L , r hh , r he , t hh , t he ] ;

A _H =[c, 1, -П 1 cos 9,0,0,0,0,0 ] ^T ;

⁰ 2 ( ® ) ^— ° BR ( ® ) =

[ ^e s2 (^ЮХ 1 3 ^a 2 ) ^e c2 ⁽ 2 ^{3 a} 2 ) ]

+ ^e c2 ^e s2 ( ® )

^e s2 ( ® ) ( 1 ^{— 3 a} 2 ) ^{— e} c2 ( ^{2 — 3 a} 2 )

—

П ( ® ) = V^e BR ИЛ2 ;

^a R,L ^(to) =

1 -

Б 1 Ц 1 sin ² 9

/^i2

(^BR (®H ±X2 H)

^k R,L ^(to) = k 0 (X ^e BR ^(ю) ^ 2 ± ^X 2 ^(to) ) ^;

11 M/X¹)-       х[Ж^-

41 — ^     ^   ; **1 — 0Q о ^   ;

к -к x ( ³ )ц( ³ )' n -Ju ( ³ )/_е( ³ ) •

/V 3 — /V0 о ^    ; ^3 — г^ о ;

₽ R,L ( ^Ю ) ^{— k} R,L ( ® ) h ^{cos 9} R,L ; ₽ 3 = k 3 h ^{cos 9} 3 ;

( \         ₽02       M A 2 k 0 P 02

• ^o s2 ( ® ) ^—o s2 ⁺ —₂—₂ ; X 2 ( ® )^——    2

• 3. Киральный метаматериал на основе составных спиральных элементов

Wq — to               to 0 — to

Явный вид матриц B h e не приводится в статье в силу громоздкости их элементов.

Из решения систем линейных алгебраических уравнений (22) определяются элементы неизвестных матриц коэффициентов отражения и прохождения основных и кросс-поляризованных компонент поля (10), (11), (12).

Рассмотрим построение частной математической модели составного элемента на основе произвольного числа спиральных элементов в пространственной конфигурации, а также метаматериала на основе матрицы таких элементов. Геометрия элемента и метаматериала отражены на рис. 3. Для упрощения на рис. 3 показаны три спирали в структуре составного компонента различными типами линий.

Спиральные компоненты внутри пространственного составного элемента различаются между собой геометрическими размерами. При этом при создании КММ на их основе все компоненты должны быть тождественными. Геометрические размеры i -го кирального компонента в составном киральном элементе: N i - число витков; R i - радиус витка спирали; h_i – шаг спирали; p_i – длина спирали в расправленном состоянии; r_i – радиус проволоки; a i - угол накрутки спирали.

Для расчета резонансной частоты составного элемента воспользуемся формулой Томсона:

to Q ^—

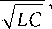
где L - общая индуктивность составного кираль-ного компонента; C - емкость составного кираль-ного компонента.

Индуктивность и емкость составного кирально-го компонента имеют вид:

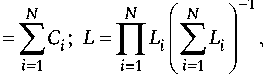
где L i - индуктивность i -го спирального компонента в пространственной структуре составного спирального элемента; C i - емкость i -го спираль-

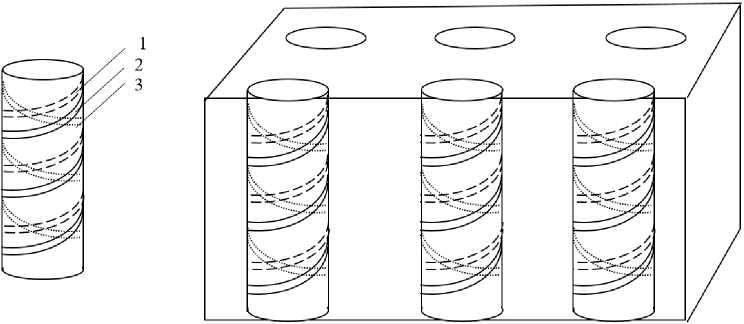
Рис. 3. Геометрия элемента и метаматериала

Fig. 3. Element and metamaterial geometry

ного компонента в пространственной стр уктуре составного спирального элемента ( i = 1, N ); N -полное количество спиралей в составном кираль-ном компоненте.

Емкость одиночной спирали с учетом ближайшего окружения элементами определяется следующим образом:

® 0 =

N  f N V

П L i Z L i i =1 V i =1 J

N

Z C i i =1

-1/2

где C_i и L_i выражаются из формул (26) и (27).

C i = C пр i + C MB i + C M3 i ,

то есть суммой емкостей тонкопроволочного прямолинейного проводника, межвитковой емкости i -го спирального компонента и межэлементной

емкости внутри спирального компонента.

В результате выражение для суммарной емко-

сти i -го спирального компонента имеет следу-

ющий вид:

C i = ^бс 2

l i

. f 2 L )

18 In i -1

I r i J

”[( R i + 2 r i ) ² - R i ² 1 ( N i -1 )

+ —-------------+ hi

+ 1 ^Ni ^{( R}i + r i ) r ", d cos a i

где s_c 2 - относительная диэлектрическая проницаемость несущей среды (цилиндрической основы, на которую накручен спиральный компонент).

Индуктивность i -го спирального компонента:

L i = ^ c2

п Ni² Ri² l_i

где ц_с 2 - относительная магнитная проницаемость несущей среды (контейнера).

Формула для резонансной частоты составного спирального компонента получается с использованием выражений (23)–(27):

4. Численные результаты

Для апробации предложенной модели КММ на основе матрицы из составных спиральных компонентов была выбрана структура, состоящая из двух составных элементов, накрученных на единую цилиндрическую основу с б c 2 = 1,6 (одна из разновидностей пенополистирола). Контейнер (несущая среда) также обладал б c 2 = 1,6. Толщина планарного слоя КММ равнялась 0,05 м. Первый спиральный элемент в составе составного ки-рального компонента обладал следующими значениями геометрических параметров: R 1 = 0,01 м, N 1 = 3, r = 0,002 м, H 1 = 0,05 м, d 1 = 0,05 м, в то время как второй элемент: R ₁ = 0, 01 м, N ₁ = 2, r ₁ = 0, 002 м, H ₁ = 0, 05 м, d ₁ = 0, 05 м, то есть спирали отличались друг от друга числом витков. Области 1 и 3 представляли собой вакуум с Б 1₃ = = Ц 13 = 1. Падение ЭМВ на исследуемый планарный слой КММ было нормальным: 0 = 0. Были для примера исследованы три случая, когда менялась концентрация киральных компонентов внутри контейнера, то есть: a 2 = 0,05; 0,1; 0,15. Также в качестве частного случая была рассмотрена ситуация, соответствующая отсутствию учета гетерогенности КММ, то есть для эффективной диэлектрической проницаемости не применялась модель Бруггемана. Падение считалось нормальным, чтобы кросс-поляризационные эффекты были незначительны.

В результате были рассчитаны частотные зависимости отраженной мощности основной компо-

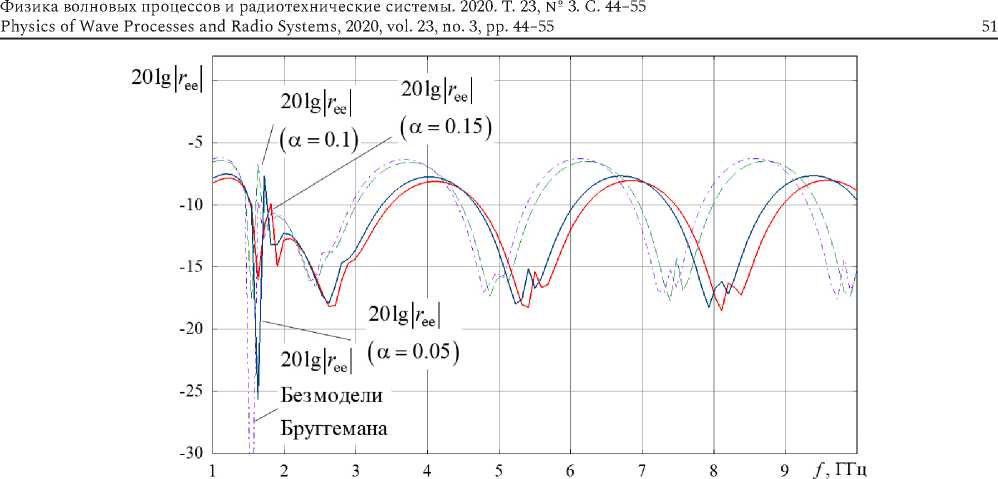
Рис. 4. Частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов

Fig. 4. Frequency dependences of the power reflected from the planar CMM layer (E-polarization) at various values of the concentration of chiral components

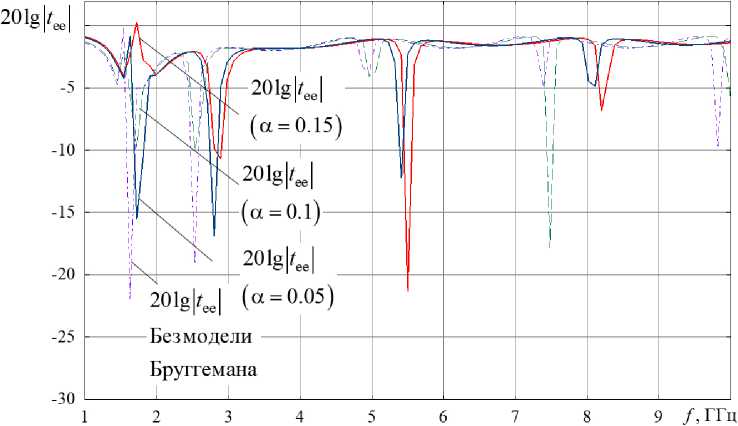
Рис. 5. Частотные зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов

Fig. 5. Frequency dependences of the power transmitted through the planar CMM layer (E-polarization) at various values of the concentration of chiral components

ненты (20lgp*_ee) и прошедшей мощности основной компоненты (20 lg | t _ee|) для случая падения на планарный слой КММ волны с E-поляризацией поля.

На рис. 4 приведены частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 10 ГГц.

На рис. 5 приведены зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 10 ГГц.

Из сравнения рис. 4 и 5 можно сделать вывод, что вблизи частоты 1,6 ГГц наблюдаются минимумы прохождения и отражения основной (падающей, Е) компоненты поля. На этой частоте ЭМП концентрируется в планарном слое КММ. Этот эффект ранее был предсказан и для КММ на основе классических многозаходных спиральных элементов.

На рис. 6 приведены частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 3 ГГц.

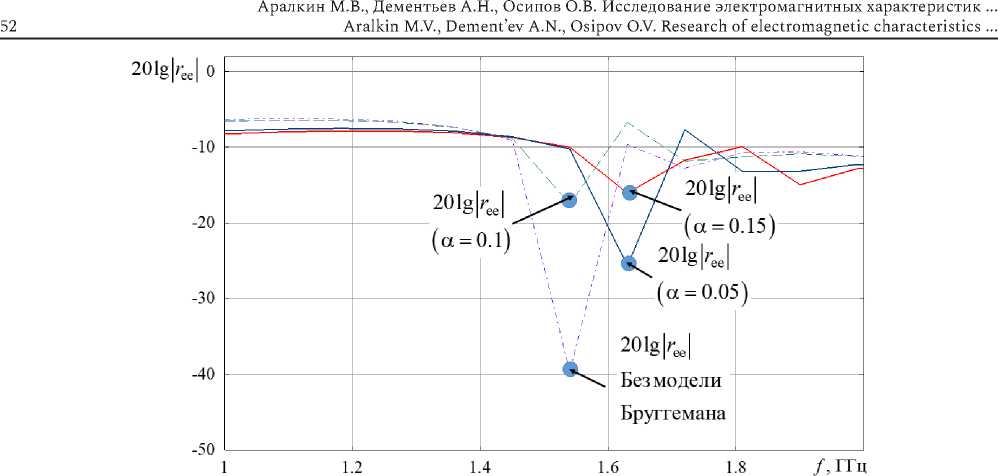
Рис. 6. Частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов

Fig. 6. Frequency dependences of the power reflected from the planar CMM layer (E-polarization) at various values of the concentration of chiral components

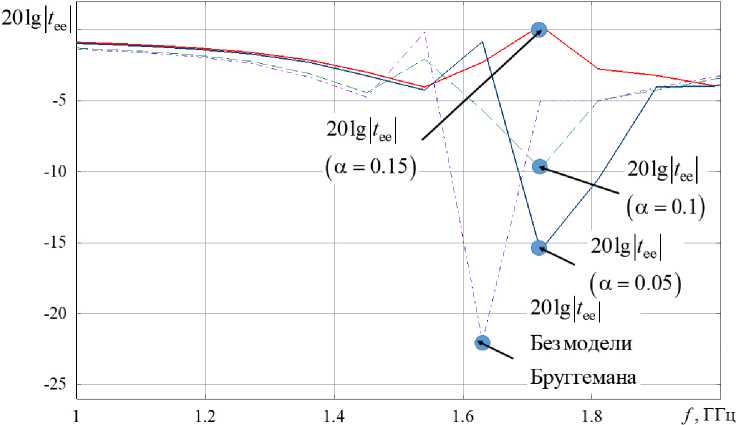
Рис. 7. Частотные зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов

Fig. 7. Frequency dependences of the power transmitted through the planar CMM layer (E-polarization) at various values of the concentration of chiral components

Как видно из рис. 6, в «предрезонансном» частотном диапазоне уровень отражения практически не зависит от концентрации киральных компонентов и результаты с использованием и без использования модели Бруггемана практически совпадают. Особый интерес представляет частотная область, в которой наблюдается резонансный минимум отражения ЭМП Е-поляризации. Как видно из представленных характеристик, расчет без учета гетерогенности приводит к минимальному значению отраженной мощности в –40дБ. Учет гетерогенности с использованием модели Бруггемана ведет к увеличению уровня отражения

ЭМП E-поляризации вблизи резонансной частоты. Кроме того, как видно из рис. 6, частоты резонансного минимума отражения, рассчитанные с учетом и без учета гетерогенности и при разных значениях концентрации, отличаются и равны 1,57 и 1,62 ГГц. Также можно заметить, что увеличение концентрации киральных компонент в несущей среде приводит к тому, что эффект захвата ЭМП планарным слоем КММ постепенно исчезает, так как растет уровень отражения основной компоненты поля.

На рис. 7 приведены зависимости прошедшей через планарный слой КММ мощности

(E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 3 ГГц.

В «предрезонансном» частотном диапазоне (см. рис. 7) уровень прошедшей мощности практически не зависит от концентрации киральных компонентов и результаты с использованием и без использования модели Бруггемана практически совпадают. Так же как и в случае исследования отражения ЭМП от планарного слоя КММ, интерес представляет частотная область, в которой наблюдается резонансный минимум прохождения ЭМП Е-поляризации. Как видно из представленных характеристик, расчет без учета гетерогенности приводит к минимальному значению прошедшей мощности в -22 дБ. Учет гетерогенности с использованием модели Бруггемана приводит к увеличению уровня прохождения ЭМП E-поляризации вблизи резонансной частоты. Кроме того, как видно из рис. 6, частоты резонансного минимума прохождения, рассчитанные с учетом и без учета гетерогенности, отличаются – 1,64 и 1,69 ГГц. Также можно заметить, что увеличение концентрации киральных компонент в несущей среде приводит к тому, что эффект захвата ЭМП планарным слоем КММ исчезает, так как при а 2 = 0,15 электромагнитная волна проходит через планарный слой КММ практически без ослабления.

Заключение

В статье построена математическая модель кирального метаматериала на основе составных тонкопроволочных спиральных элементов, учитывающая свойства киральности, гетерогенности и дисперсии. В результате решения задачи об отражении плоской электромагнитной волны линейной поляризации от планарного слоя показано, что метаструктура обладает выраженными частотно-селективными свойствами. В частности, обнаружены частотные режимы, в которых метаматериал позволяет преобразовывать нормально и радиально падающее электромагнитное излучение СВЧ в рассеяние в плоскости структуры. Подобный эффект может быть использован для создания частотно селективных концентраторов (хабов) СВЧ-энергии.

В статье доказано, что использование модели Бруггемана для учета гетерогенности корректирует значение уровней прошедшей и отраженной мощностей при падении ЭМП на планарный слой КММ в сторону их увеличения. Рост концентрации киральных компонентов в контейнере приводит к исчезновению эффекта частотно-селективной концентрации электромагнитной энергии СВЧ-метаматериалом.