Исследование энергетических процессов в зоне резания при абразивно-экструзионной обработке

Абразивно-экструзионная обработка (АЭО) представляет собой вид финишной обработки, применяемый в основном для обеспечения качества поверхностного слоя в сложнопрофильных и труднодоступных каналах деталей летательных аппаратов.

Сущность обработки заключается в перепрессовыва-нии рабочей смеси, состоящей из полимера наполненного абразивом, вдоль обрабатываемой поверхности. На современном этапе развития технологии АЭО в качестве основного компонента рабочих смесей используется синтетический каучук теплостойкий (СКТ).

Известно, что тепло, выделяемое в процессе обработки, активно изменяет реологические свойства каучука, уменьшая его вязкость. Что приводит к уменьшению силы закрепления абразивных зерен и силы резания вплоть до прекращения процесса отделения стружки. Аналогично тепло действует и на масло в системе гидропривода установки, что также ведет к потере давления и уменьшению силы резания. В результате возникает нестабильность режимов обработки и невозможность массового использования данной технологии в промышленности.

Для получения более ясной картины проведен анализ тепловых процессов в технологическом оборудовании, в результате которого определены и охарактеризованы все источники и стоки теплоты, возникающие в узлах и агрегатах установки в процессе экструзионной обработки. Составлено уравнение теплового баланса, которое для установившегося режима работы выглядит следующим образом:

верхностью и межслойного трения внутри рабочей смеси - О .

р

Известно, что энергия, подведенная к телу в данной термодинамической системе, идет на совершение работы, а также на увеличение теплоты этой системы:

^E = Q + L,                (4)

где ^Е - энергия, подведенная к системе; Q - тепловые потери^ - полезная работа.

При АЭО величинаL представляет собой работу потока, которая состоит из работы экструзииL‘ и механической работыLm (работы трения и резания-оттеснения активными абразивными зернами):

L=K+L_m.              (5)

Рассмотрим перемещение в канале элементарной массы рабочего тела dm из сечения 1-1в сечение 2-2 за время dT (рис. 1).

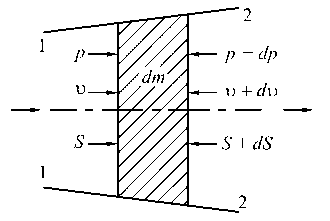
Рис. 1. Схема движения элементарной массы при АЭО

С о ₆ щ1

q_r . общ2

При этом теплоприток определяется по формуле

О .

= ^ р +^ тр ⁺^ н _M ^,

где 2общ1- общее тепло, получаемое системой; 2р- теплоприток, возникающий в приспособлении от взаимодействия рабочей смеси с обрабатываемой поверхностью; 2тр - теплоприток от трения поршней по цилиндрам; 0нм - теплоприток от внешнего источника - масла;

теплоотток:

C_o6 щ2 =^_м+^_к+^ вн ^, (³)

где б_общ2- общее тепло, отдаваемое системой; О_м - теплоотток в абразивную массу; Q - теплоотток в деталь, приспособление и металлоконструкции установки; О - теплоотток во внешнюю среду.

Опытным путем установлено, что наибольшее влияние в зоне резания оказывает теплоприток от контакта активных абразивных зерен с обрабатываемой по

На левой грани внешнее давление^ совершает работу перемещения элементарной массы; на правой грани внешнее давление^ + dp, направленное навстречу движению тела, носит характер сопротивления, преодолевая которое тело совершает работу. Поэтому первую работу следует рассматривать как отрицательную (по отношению к телу), а вторую - как положительную. Алгебраическая сумма этих двух работ есть работа проталкиванияL‘, Дж.

Таким образом, за время dt рабочее тело массой dm совершает работу dL‘ dT = [(p + dp)(S + dS)(u + du) -pSu] dT, (6) где S- поперечное сечение канала, м2; и - скорость потока, м/с.

Пренебрегая бесконечно малыми величинами второго и высшего порядка, после преобразования получим 8L' =pSdu + pudS + uSdp =pd (Su) +

+ (Su) dp= d [p (Su)] = d (pF).          (7)

В интегральном виде работа экструзии составляет

L ' = Г / d ⁽ P^V ) = ^Р 2 ^V 2 - PV 1 ’         (⁸)

pV1

где р - давление рабочей смеси (PC), Па; V- объем PC, м³. Техническая работа^ зависит от силы резания активными абразивными зернами P_yz.

Таким образом, из условия энергетического баланса теплоприток при АЭО будет определяться формулой

N = E-V(p₂-p_v)V + P_yz- l^/т,         (9)

где А мощность источника теплоты, выделяющейся в приспособлении при АЭО, Вт;р - давление на входе в канал, Па; p ₂ - давление на выходе из канала, Па; V- объем рабочей смеси, м³; E - мощность, необходимая для перепрессования рабочей смеси вдоль обрабатываемой поверхности, Вт; т - время обработки, с; l_k - длина канала, м;P_уz- сила резания единичным абразивным зерном, Н.

Для определения контактной температуры в зоне резания схематизируем источник, связанный с обработкой активными абразивными зернами, в виде модели элемента абразивного зерна.

Пусть модель активного абразивного зерна 1 взаимодействует с поверхностью образца 2 (рис. 2) и перемещается по отношению к последней со скоростью и, м/с. Как результат работы трения, резания и деформации поверхностных слоев металла возникает теплота, одна часть которой поступает в зерно, а другая - в образец.

шению к которому источник неподвижен, описывается дифференциальным уравнением

дб    д ² б

— = ®—г , дт    д у у

при начальном условии с (у,0) = Ои граничных условиях q(0;T) = q и q(^.i) = О (пассивная граница отнесена в бесконечность, то есть теплоотдача отсутствует).

Задача решается с помощью двух интегральных пе

реходов. Поскольку в стержне теплота распространяется только в направлении ОХ, то процесс в нем представ

ляем как часть процесса распространения теплоты в полупространстве, на поверхности которого непрерывно в течение ограниченного времени действует неподвижный, плоский, двухмерный источник, имеющий бесконечную протяженность по направлениям двух других осей координат.

Фундаментальное решение дифференциального уравнения теплопроводности для температурного поля, возникающего под действием теплоты, внесенной импульсом в виде мгновенного точечного источника, описыва

ется выражением

N ^{б (} x , у , z , t ) =       --- —- exp

W® (4 -п t ) ³²

R¹ _- 4 ® t

где б(х, у, z, t) - температура точки тела с координатами^,

у, z, возникающая через t с после того, как в точке с коор

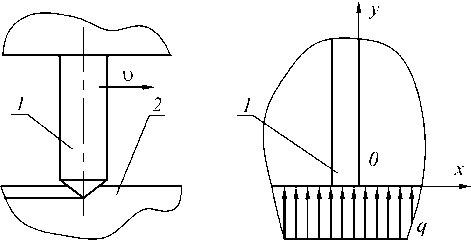
а                             б

Рис. 2. Процесс взаимодействия единичного абразивного зерна с обрабатываемой поверхностью: а - модель процесса; б - ее схематизация

динатами х_и, у_и, z_u имел место тепловой импульс; r = 7 ( x _u - x ) ² + ( у _и - у ) ² + ( z _и - z ) ² - расстояние от точки до источника, м; X, ® - теплофизические характеристики тела, соответственно Вт/(м-град) и м²/с.

С учетом формулы (11) для первого интегрального

перехода найдем

^б ( У , t ) =

2 N

+L

W® (4 п t )^3/2 -L

2 N

= — I      exp

1^® (4 л )³²    |

—

⁽ x u ^- x ^{)2 + (} У и ^- У ^{)2 + ( z} и

- z )²

4 ® t

^dx и =

dx и •

Цифра 2 в числителе проставлена в связи с тем, что источник действует не в неограниченном теле, а на адиабатической поверхности полупространства.

Рассмотрим интеграл

+L

J = J exp

-L

( С - x ^{) 2} 4 ® t

dx _u •

Схематизируя процесс теплообмена, мысленно представляем зерно как стержень (индентор), на рабочем торце которого действует источник равномерной плотности q, Вт/м². Верхний конец индентора полагаем пассивной границей, поскольку температура здесь сохраняется одной и той же, равной температуре окружающей среды. Так как длительность контактного взаимодействия обрабатываемой поверхности и индентора не превышает нескольких секунд, предположим, индентор отдает в окружающую среду столь незначительное количество теплоты, что его боковые граничные поверхности можно считать адиабатическими, то есть не имеющими теплообмена с окружающей средой. Поскольку теплоотдачи с боковой поверхности индентора нет, теплота, внесенная источником q, распространяется только вдоль оси Оу и процесс в контакте поверхности со стержнем, по отно

Применив подстановку

x - x 1      7 Гл--- и---= u; dx„ = duN 4®t

V4®

и имея в виду, что

U 2

f exp I - p ² u ² I du =-- [ Ф( pu ₂) - Ф( pu 1 ) ] ,

2 p u1К где Ф(ри) - функция интеграла вероятности Гаусса, получаем +L/

-L

Подставляя значение/в выражение (12) и выполняя аналогичное интегрирование поzu, получаем

^{б (} У , t ) = —r= ^exP Мп t

^^^^в

⁽ У и ^- У ^{) 2}

4 ® t

•

Для точек, расположенных на торце стержня (у = 0), в том случае, когда здесь же расположен источник (уи= 0), имеем

N ω 6 (0, t ) = -^.               (16)

λπ t

Формулы (15) и (16) описывают температурное поле в стержне, возникающее под действием мгновенного плоского источника, вносящего в тело N, Дж/м². Поскольку источник, интересующий нас в рассматриваемой задаче, действует не мгновенно, а в течение времени т пока индентор находится в контакте с образцом, то требуется выполнить второй интегральный переход:

6 (0, т ) = q ^L^,          (17)

λπ0 τ-t где q - плотность непрерывно действующего источника, Вт/м2, заменившая мощность источника теплоты Nв выражении (16); т - время наблюдения, т. е. момент времени, для которого ведется расчет температуры тела; t - время каждого элементарного импульса в период 0 < t < т. Разность (т -t) соответствует промежутку времени, в течение которого теплота, внесенная элементарным импульсом, распространяется в стержне.

Интегрируя выражение (17), получаем формулу для расчета температуры в контакте активного абразивного зерна с обрабатываемой поверхностью:

2 q ω θ (0, τ ) =         τ .

λπ

С учетом равномерного распределения плотности источника, т.е. q = N/F, где F- площадь контакта, получим 6 (0, т ) = 2N^ 7Г,            (18)

F⋅λ π где N- мощность источника теплоты, выделяющейся в приспособлении при АЭО, вычисленная по формуле (9).

С целью подтверждения теоретических данных и определения реальных температур, возникающих от действия источника тепла при течении рабочей смеси вдоль поверхностей образца и приспособления за счет трения, пластического оттеснения и резания активными абразивными зернами, а также межслойного трения рабочей смеси, спланирован следующий эксперимент.

Задача эксперимента - изучение зависимости количества выделяемого тепла от времени обработки.

Образец 2 (18 • 25 • 4 мм), изготовленный из стали 12Х18Н10Т, установлен во вкладыше 5 (рис. 3) и закреплен в корпусе приспособления 3 стопорными кольцами. Для определения температуры внутри приспособления использован платиновый термометр сопротивления 4 с регистрацией температуры прибором КСМ-4. Давление рабочей смеси контролировалось двумя датчиками давления 7 с записью параметров на осциллограф. Измерение температуры масла в системе управления регистрировалось во времени для определения выхода установки на установившийся режим. Измерение температуры смеси и масла, а также давления РС выполнялось непрерывно в течение 60 мин. Опыты проведены с 6-ти кратным повторением (т = 6) [1].

Математическая обработка результатов экспериментов дала следующие зависимости температур смеси Т_сми масла Т_мво времени (рис. 4).

Абсолютная погрешность эксперимента при количестве опытов т = 6и доверительном интервале Р = 0,95 составляет Ах = 0,558 °С.

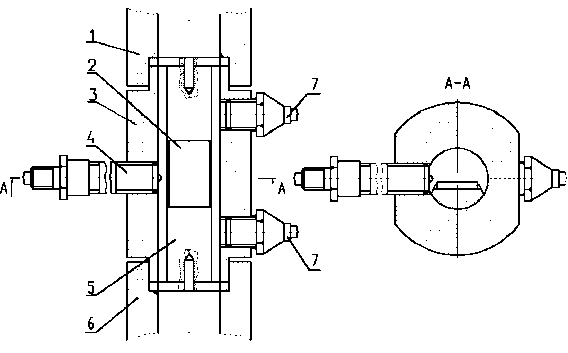
Рис. 3. Приспособление для АЭО на лабораторной установке УЭШ-25: 1 , 6 - верхний и нижний цилиндры установки;

2 - образец; 3 - корпус приспособления; 4 - термометр сопротивления; 5 - вкладыш; 7 - датчики давления ДДИ-20

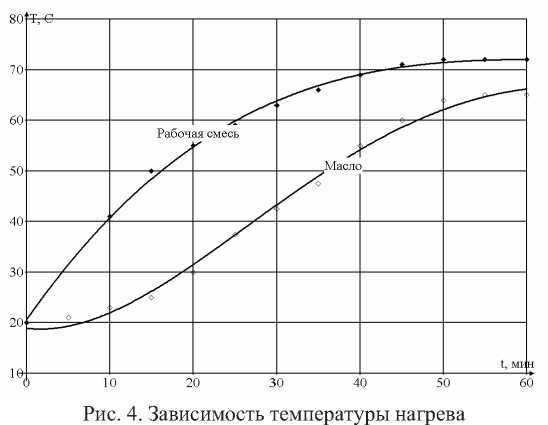
рабочей смеси Т_сми масла Т_мот времени обработки t : Т_см= 20,62+ 2,34t-0,04t ² + 1,77 • 10 ⁴ Г: Т_м= 18,92 - 0,19t + + 0,06t ² - 9,75 • 10 ^-4 t ³ + 4,52 • 10 ^-6 t ⁴

Сравним температуры, рассчитанные по теоретической формуле (18), и температуры, измеренные на практике (эмпирическая зависимость):

⁶ ,

2 N ω

F ⋅λ π

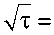
2 ⋅ 112 7 ⋅ 10 ^{- 6} ⋅ 2700

0, 028 ⋅ 11, 68 ⋅ 3,14

= 53,13 ^ОС

С учетом начальной температуры 21 °С через 45 мин смесь нагреется до 74,13 °С. На практике 71 °С. По эмпи рической зависимости:

Т = 20,62+ 2,34t-0,04t²+1,77 • 10^ = 20,26 + см

+ 2,34 • 45 - 0,04 • 45 + 1,77 • 10 4 45 = 70,53 ОС.

Таким образом, результаты, полученные теоретически, расчетами по эмпирическим формулам и измеренные на практике, отличаются менее чем на 5 % (максимальный размах 4,4 %).

Определяя при помощи зависимостей, полученных в результате экспериментов, мощности тепловых источников и температуры в зоне резания, появляется возможность рассчитывать теплообменное оборудование, стабилизирующее процесс абразивно-экструзионной обработки.

Кроме того, дальнейшее развитее технологии предполагает использование полученной модели для создания системы управления режимами абразивно-экструзионной обработки при помощи изменения реологических свойств рабочей смеси, путем автоматического регулирования температуры процесса.