Исследование касательных напряжений в приопорной зоне стальной балки, предварительно напряженной вытяжкой стенки

На стадии предварительного напряжения тавр представляет собой составной стержень, состоящий из двух отдельных стержней, в котором пояс сжат, а верхние волокна стенки растянуты, поэтому в шве составного стержня возникают сдвигающие усилия. По теории А.Р. Ржаницина [3], в составном стержне, длина которого значительно превышает высоту его полного сечения, влияние поперечных деформаций в отдельных стержнях должно быть невелико.

На первом этапе предварительного напряжения стенка растягивается усилием N_o = A_wR_y до напряжения, равного расчетному сопротивлению материала стенки. После присоединения верхнего пояса и снятия усилий предварительного напряжения стенка за счет обратных упругих деформаций обжимает сечение тавра напряжением а ₀. Сжимающее напряжение а ₀ создает в поясе усилие N f = а₀ A f, а в стенке - усилие, равное а₀ A_w . Так как центр тяжести тавра по отношению центра тяжести стенки смещен на расстояние у '₃, то создается изгибающий момент M_o = N_oy '₃ (рис. 1).

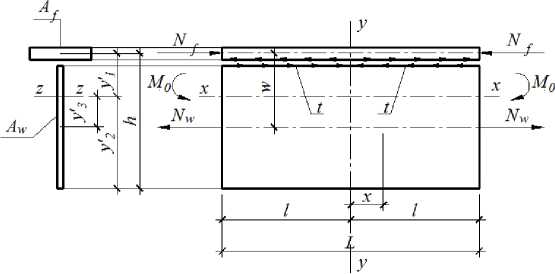
Рис. 1. Расчетная схема и эпюра усилия сдвига на контакте «стенка ‒ пояс» в тавре на стадии изготовления

Определим сдвиговые усилия, возникающие на контакте «стенка ‒ пояс» на стадии предварительного напряжения тавра.

Выразим усилие, сжимающее пояс, Nf через коэффициент асимметрии тавра K0 и через расчетное сопротивление материала пояса Ry :

A

K 0 - 1 _=R   A w A f

K о +1     ^y A w + A f ■

N f = а о A_f = N о — f- = N о f       A w ^{+ A}f

Поскольку на стадии преднапряжения стенка растягивается усилием N , а затем сжи- мается усилием, равным а0Aw, тогда полное усилие Nw, действующее на стенку, будет:

N w = а о A w - N о = N о

f Aw

^

-1

I A w + A f   J

^{- N} о

^K о ^{- 1}

K о +1

- R y

A w A f

A w ⁺ A f

Во время работы составного стержня в связях сдвига каждого шва возникают усилия, являющиеся функциями координаты x , отсчитываемой по длине стержня. Значение этих усилий, отнесенное к единице длины шва, обозначим t Н / м . Благодаря наличию абсолютно жестких поперечных связей данная система эквивалентна совместно изгибаемым отдельным стержням по одной и той же кривой изгиба у ( x ).

Полный изгибающий момент в системе равен:

M = M _o + М .

Момент, вызванный сдвигающим усилием в связях сдвига в составляющих стержнях, равен:

M _Т =- T to ,                                 (4)

где T ‒ суммарное сдвигающее усилие в шве, накапливаемое по длине стержня от начала стержня до рассматриваемого сечения; ш = h /2 - расстояние между центрами тяжести сечений двух смежных стержней, разделенных швом; h ‒ высота составного стержня (тавра). Тогда изгибающий момент M , образовавшийся в результате смещения центра тяжести тавра по отношению центра тяжести стенки, выраженный через коэффициент асимметрии тавра K и через расчетное сопротивление материала стенки R , примет следующий вид:

M_o = — Ny *з = — N o ш K ^-¹ = - R ш A A „               „   K о + 1      y   A_w + A ,

Продольные силы в поясе и стенке выражаются формулой:

N , = N f - T ; N w = N w + T ,

.

где N ^f и N ^w ‒ продольные силы, вызываемые в поясе и стенке только нагрузкой.

Усилия в поперечных связях являются уравновешенными и ничего не добавляют к общему изгибающему моменту составного стержня.

Решение уравнения сдвиговых усилий T можно представить в виде:

Аю ( chAx).

T                  I

А,Д chAl

А 10 = N W /( E w A ) - N ' /( E , A , ) - M „ ш /( £ EL, );

А„ = 1 /( E,A ) + 1 /( E , A , ) + ш ² /( £ EI , ),

где T ‒ суммарное сдвигающее усилие в шве, накапливаемое по длине стержня от начала стержня до рассматриваемого сечения.

С учетом формул (1), (2), (3), (9) и (10) выражение (8) примет вид:

t =- NKzL ( chAL _ i 1 .

⁰ K + 1 ( ch A l   )

Максимальное значение распределенного касательного усилия t наблюдается у тор- цов составного стержня при x = l = L /2 :

t max

^{- N} 0 ^A

к

^K 0 ^{- 1}

K о + 1

^               (

thAl = - RyAwX )              к

K 0Z 1 1

^K о ^{+ 1} )

th A l .

Для определения касательных напряжений на стадии предварительного напряжения стальной балки вытяжкой стенки необходимо рассмотреть напряженное состояние по нормальным и касательным напряжениям и их взаимовлияние в сечениях стальной балки при действии на нее сдвигающих сил по схеме на рисунке 2. Нормальные напряжения на рас- стоянии z от начала координат:

^ = T + Ty^

Izt

.

Для оценки касательных напряжений воспользуемся методикой, изложенной И.Ю. Белуцким [1] для случая балки таврового сечения при действии касательной нагрузки. Поскольку сдвигающие усилия действуют только на контакте пояса и стенки, геометрические параметры пояса можно не учитывать и считать, что касательные усилия действуют только на верхнюю кромку стенки. Выделим для этого в стенке тавра участок с вертикальными сечениями I - 1, II - II и горизонтальным сечением III - III и рассмотрим условия ее равновесия (рис. 2).

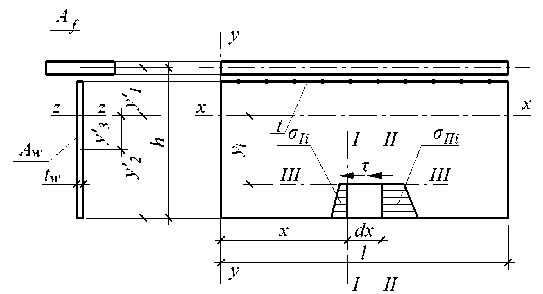
Рис. 2. Схема загружения стальной балки на стадии предварительного напряжения касательными усилиями

Нормальные силы по сечениям I —I и II — II в пределах у\ — у*2 равны соответ- ственно:

N II — II

^Ni — I

= J a,dA ₀ = Tt wj dy + T^tw- J ydy ; A о                     0 — ^у ’₂              zt    - ^у ’₂

= J a_n, dA₀ = ( T + tdx ) t,

A 0

w

к

- у ' ,

T . +£ 0 — y’₂       ¹ zt

- y\

J ydy .

- У’ 2

Составляя условие равновесия ^ z = 0, получим:

N II — II ~ N I — I = ^T pr • t w dx .

Заменив N и N , находим выражение для касательных напряжений, распределенных по высоте стенки в пределах у ' ₂<  у’_t <  у ' _х:

T = t • pr

⁽ У ' 2 ^— У' i )

A 0

— fl ( у 2 — /2 ) = t • ² I zt              _

— J dy + ^ 1 A 0 —^J y ' 2        I zt

У’,

J ^ydy .

- У \      _

При определении конкретной величины t ординаты у '_г, у \ , у\ следует подставлять со своим знаком в соответствии с направлением осей, принятым на рисунке 3.

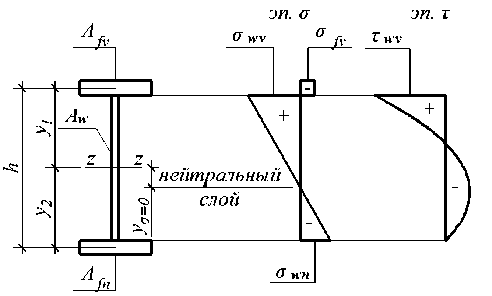
Рис. 3. Эпюры нормальных и касательных напряжений на стадии предварительного напряжения балки

Необходимо верхний предел интегрирования установить постоянным и равным расстоянию от центра тяжести тавра до верхней кромки тавра относительно y ' , а нижний предел установить изменяемым по высоте тавра и равным y ' :

^Т pr = t '

тИ + г

^A0 - y '2      z«

y ' i

j ydy = t ■

^- y 'г

—

/

V

—( y '1 + y \ )+ - ^{y j}- ( y '2 -

A 12      1

2 I_zt

y '₁                      y '₁

т j dy + ^yf j ydy _ A ⁰ yV         I zt y-,

■ y '2) ] .

7_

—

Определим касательные напряжения в предварительно напряженной стальной балке двутаврового сечения от внешней нагрузки.

По теории [4] касательные напряжения от внешней нагрузки т_у будут равны:

y ₁

^T zy = ^T yz = ^j y ^dA .

Iztw yi

Запишем выражение для предварительных касательных напряжений, распределенных по высоте стенки, в пределах y \ <  yV < у *₂:

T = t ■ pr

y ' 1                      y ' 1

A j dy ⁺ 7¹ j ydy

0 y ' _i              zt y ' _i

—

/

V

—(y'i + y'2)+(y'1 -y'2)

W 1      2 / T V 1      2 /

A 0              2 Izt7

где t ‒ распределенное касательное усилие, приходящееся на единицу длины шва, полученное по формуле.

Чтобы представить выражение (20) в виде суммы интегралов в пределах y, <  y_t <  y ₂, необходимо функцию y сдвинуть на расстояние между центрами тяжести тавра и двутавра, равное y , тогда формула (20) примет вид:

^Т pr = t '

г

V

A ₀

-

y ' ₁ y_c I zt

y ₁

j dy + Г

⁷ y        z*

zt yi

y ₁

j ydy

-

' h + y^h ( y \ - y 2 ) ] ,

V A о    ² I zt           7

где У с = У 1

—

₌    hK ( 2 - Y w ( K + 1 ))

^{y 1}   ( K + 1 )( 2 K + Y w ( K + 1 )) .

Выразим по методике [2] геометрические параметры тавра через параметры двутавра: ‒ площадь поперечного сечения тавра:

A ( 2 K + Y w ( K +1 )).

2 ( K + 1 )

‒ коэффициент асимметрии тавра:

;

2 K

^{K 0}    Y w ( K + 1 ) ;

‒ расстояние от центра тяжести тавра до верхней точки тавра:

У '1 =

h

hY w ( K + 1 )  .

( K 0 + 1 )   2 K + Y w ( K + 1 ) ’

‒ момент инерции тавра:

Izt

A o h ² ( 2 K о - 1 ) Ah ² Y w ( 4 K - Y w ( K + 1 )) =--= ------ ■ --;------------:-------^--

3   ( K 0 + 1 ) ²      6     ( 2 K + Y w ( K + 1 )) ’

где K ‒ коэффициент асимметрии двутавра; A ‒ площадь поперечного сечения двутавра;

Y - коэффициент распределения материала по стенке двутавра.

Таким образом, получим общее суммарное выражение касательных напряжений ts , распределенных по высоте стенки, возникающих в предварительно напряженной стальной балке при работе на изгиб:

т = т + г s      pr     zy

t

•

A ( 4 K - Y . ( K + 1 ))

y ₁

2(2K - 1)J dy + yi

+ ^f 6 ⁽ K ⁺ 1 )  У ^а У — h ⁽ K + 1 )

^             ^ y=                       .

y 1

iT^yd A '

I_z t_{w y i}

Максимум распределенного касательного усилия t у торцов стержня при x = l = L /2 будет равен:

t max = - ^Ry^Aw ^

^{2 K} Y w ^{( K +} 1 )

( 2 K + y . ( K + 1 ) J

th X l .

Наибольшее значение касательных напряжений от внешней нагрузки т в стенке балки получается для точек, расположенных на нейтральной оси. Нейтральной осью будем считать ту, на которой величина нормальных напряжений от внешней нагрузки будет равна нулю, т.е. при yt = y^0 = 0. Таким образом, будем считать высоту двутавра равной высоте стенки, тогда значение максимальных касательных напряжений т^ на торце предвари- тельно напряженной двутавровой балки при работе на изгиб будет равно:

т = т     + т max       pr, y,=0      zy, y,=0

'max ' ^{2 ( 2 K} — 1 )    L^

A ( 4 K - Y w ( K + 1 )) ,. I dy +

'    t_ • 6 К + 1 )    + 6 Q     ( K + 1) 2     1 y .

.Ah(4K — Yw(K +1))  Ah2  6K - Yw(K +1)2 J,_yy tm • h(K +1)  + 3Q(2K - Y. (K +1))

A ( 4 K - Y . ( K +1 ))   A y . ( 6 K - Y . ( K +1)² ) ^.

Таким образом, формула (28) выражает интегральный закон распределения максималь- ных касательных напряжений т^ на торце предварительно напряженной двутавровой балки при работе на изгиб по высоте двутавра на уровне нейтрального слоя двутавра yt = y^0 = 0, где значение касательных напряжений от внешней нагрузки наибольшее.

Решим интегральное уравнение (28) в пределах y _t<  y_t <  y_{a= 0}:

₌ t max h        K ( 2 - K )         3 Q     K ( 2 - Y . )

“ A  ( 4 K - y . ( K + 1 ))( K + 1 )   A   y . ( 6 K - Y . ( K + 1) 2 ) '

Таким образом, решение выражения (29) позволяет определить величину максимальных касательных напряжений т^ на торце предварительно напряженной двутавровой балки любого поперечного сечения.

Выражение касательных напряжений двутавровой балки без предварительного напряжения при работе на изгиб будет иметь вид:

₌ QS       3QK ( 2 - Y . )

’■ I Л.   A T. ( 6 K — .. ( K + 1) 2 )'

Определим влияние предварительного напряжения на величину максимальной поперечной силы, действующей в опорной зоне стальной балки двутаврового сечения. Величину максимальной поперечной силы Q    для двутавровой балки без предварительного напряжения, представленную в (30), определим из условия прочности на срез, принимая г = R , тогда: zy, max       s ,

_ 4 3 R , A y . ( 6 K - Y . ( K + 1) 2 ) zy ^,ma x             9 K ( 2 - y )

.

Величину максимальной поперечной силы Q для двутавровой балки с предварительным напряжением определим из условия прочности на срез, принимая т^ — R. , тогда:

₌ Л /3 R y A y . ( 6 K - Y ( K + 1) ² )

pr ^,ma x             9 k ( 2 - _у . )         ^x

₁₊ з/3 Y . ^hK ( 2 - K )( 2 K - y ( K + 1>Xl

( 4 K - у . ( K + 1 ))( K + 1 )( 2 K + y . ( K + 1 ))

Разделим (31) на (32), получим отношение максимальных поперечных сил Q и

Q_Zy max , выраженное через некоторый параметр a_Q :

Q pr ,max Q zy ,max

₁₊ v 3Y,AhK ( 2 - K X2 K - y . ( K + V fi thAl ( 4 K - y . ( K +1 ))( K +1 )( 2 K + y . ( K +1 ))

— 1 + a q .

Можно сделать вывод, что вследствие предварительного напряжения вытяжкой стенки двутавровой балки происходит увеличение максимальной поперечной силы, действующей в опорной зоне двутавровой балки, на некоторую величину a , тогда в общем виде изме- нение запишется:

Q pr ,max

^{( 1 +} « Q ) " ^Qz, ,max .