Исследование кинематики манипулятора параллельной структуры (дельта-механизма)

В некоторых областях техники перспективным является применение роботов-манипуляторов на основе механизмов параллельной кинематики, используемых при механической обработке изделий сложной формы (например, штампов, пресс-форм, лопаток турбин и т. д.), когда требуется перемещение инструмента по пятишести координатам.

В отличие от традиционных манипуляторов, структуры с параллельной кинематикой содержат замкнутые кинематические цепи и воспринимают нагрузку как пространственные фермы [1], т. е. звенья этих механизмов работают на растяжение и сжатие, что обеспечивает жесткость всей конструкции и, как следствие, повышение точности позиционирования схвата [2].

Достоинствами манипуляторов, построенных на основе параллельных механизмов, являются большая точность и жесткость, высокие рабочие нагрузки [3].

Среди недостатков этих манипуляторов следует отметить использование большого количества приводов и более сложных систем управления, меньший размер рабочей области и высокую стоимость, сложность в проектировании. Однако эти недостатки не являются препятствием для распространения параллельных манипуляторов в тех областях, где требуется точное позиционирование, высокие нагрузки и маневренность [3].

Математические и имитационные модели кинематики и динамики некоторых параллельных механизмов, а также задача оптимизации их формы и размеров рассматривались в [4].

Трехмерное моделирование кинематически сложных механизмов целесообразно выполнять с помощью системы автоматизированного проектирования (САПР) CATIA, в которой используются алгоритмы моделирования движения кинематически сложных механизмов, таких как устройства параллельной кинематики. Для решения систем уравнений, описывающих положение устройства параллельной структуры, наиболее подходящим является программный пакет Maple – система компьютерной алгебры, позволяющая решать сложные системы уравнений как в численном, так и в символьном виде. В работе [5], в которой рассматривались особенности динамики манипуляторов параллельной структуры и переходные процессы, для расчета параметров управления приводами механизмов применялся программный комплекс MATLAB/Simulink.

Постановка задачи. Рассмотрим устройство параллельной кинематики – дельта-механизм (рис. 1), включающий в себя основание, образованное точками 3 , 6 , 9 , верхнюю платформу, на движение которой накладывают ограничения три кинематические цепи: 1 – 2 – 3 , 4 – 5 – 6 , 7 – 8 – 9 . В точках 1 , 2 , 4 , 5 , 7 , 8 установлены поворотные шарниры с одной вращательной степенью свободы, в точках 3 , 6 , 9 – сферические шарниры с тремя вращательными степенями свободы. Основание и поворотная платформа представляют собой равносторонние треугольники.

Введем следующие обозначения элементов дельтамеханизма (см. рис. 1):

• -    x ij , y ij , z ij – координаты i -й точки в j -й системе координат;

• -    l i – длина i -го звена, во всех кинематических цепях l 1 = 37 мм, l 2 = 58 мм;

• -    φ ij – угол i -го шарнира в j -й кинематической цепи;

• -    δ i – угол между первой системой координат i -й кинематической цепи и базовой системой координат, δ 1 = 330°, δ 2 = 210°, δ 3 = 90°;

• -    E – расстояние между сферическими шарнирами 3 , 6 , 9 дельта-механизма, E = 60 мм;

• -    F – расстояние от начала базовой системы координат до поворотных шарниров 1 , 4 , 7 , F = 60 мм;

• -    R – расстояние от полюса схвата P до сферических шарниров 3 , 6 , 9 , R = 34,641 мм;

• -    Х 0 Y 0 Z 0 – базовая система координат;

• -    Х 1 Y 1 Z 1 – первая система координат.

Рис. 1. Общий вид дельта-механизма (обозначения см. в тексте)

Решение прямой задачи кинематики. Прямая задача кинематики манипуляторов применительно к дельта-механизму сводится к нахождению координат поворотной платформы при заданных длинах звеньев l 1 , l 2 и углов поворотов шарниров φ 11 , φ 21 , φ 12 , φ 22 , φ 13 , φ 23 (рис. 2).

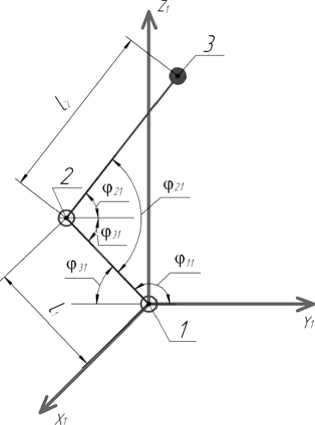
Рис. 2. Определение положения точек 2 и 3 в первой системе координат

Для решения этой задачи сначала находят координаты сферического шарнира (точки 3) в первой системе координат X1Y1Z1, а затем с помощью переноса на расстояние F и поворота на угол δ переходят к базовой системе координат X0Y0Z0. Аналогично определяют координаты остальных сферических шарниров – точек 6, 9, которые вместе с точкой 3 задают плоскость поворотной платформы (рис. 3). По уравнению этой плоскости можно найти углы ее наклона в базовой системе координат X0Y0Z0, а также высоту полюса схвата.

Рис. 3. Схема положения плоскости поворотной платформы в базовой системе координат

В первой системе координат X1Y1Z1 координаты точки 3 определяются по уравнениям x31 = 0,

• У 31 = l i

z 31 = ¹ 1

■ cos ( ф_п ) + 1 2 ■ cos ( ф ₂₁ + ф_п - 180 ° ) ,

■ sin ( ф ₁₁ ) + 1 ₂ ■ sin ( ф ₂₁ +ф ₁₁ - 180 ° ) .

При переходе от первой системы координат X 1 Y 1 Z 1 , связанной с кинематической цепью 1 – 2 – 3 , к базовой системе X 0 Y 0 Z 0 следует выполнить перенос на расстояние F и поворот на угол δ (см. рис. 1). Для уравнений координат точки 3 этот угол равен углу δ 1 , т. е. 330°:

x ₃₀ = ( 1 1 ■ cos ( ф 11 ) + 1 2 ■ cos ( ф ₂₁ +фц - 180 ° ) - F )sin ( S 1 ) , У 30 = ( 1 1 ■ cos ( ф 11 ) + 1 2 ■ cos ( ф 21 +фц- 180 ° ) - F )cos ( 5 1 ) , z 30 = 1 1 ■ sin ( ф 11 ) + 1 2 ■ sin ( ф 21 +ф 11 - 180 ° ) .

Аналогично находят координаты точки 6 в базовой системе координат X 0 Y 0 Z 0 :

•

x 60 = ( 1 1 ■ cos ( ф ₁₂ ) + 1 ₂ ■ cos ( ф ₂₂ +ф ₁₂ - 180 ° ) - F )sin ( 5 2 ) , У 60 = ( 1 1 ■ cos ( ф 12 ) + 1 2 ■ cos ( ф 22 +ф 12 - 180 ° ) - F )cos ( 5 2 ) , z 60 = 1 1 ■ sin ( ф 12 ) + 1 2 ■ sin ( ф 22 +ф 12 - 180 ° ) .

Координаты точки 9 в базовой системе координат X 0 Y 0 Z 0 задаются уравнениями

•

x ₉₀ = ( 1 1 ■ cos ( ф ₁₃ ) + 1 ₂ ■ cos ( ф ₂₃ +ф ₁₃ - 180 ° ) - F )sin ( 5 ₃ ) , y ₉₀ = ( 1 1 ■ cos ( ф ₁₃ ) + 1 ₂ ■ cos ( ф ₂₃ +ф ₁₃ - 180 ° ) - F )cos ( 5 ₃ ) , ^z 90 = ¹1 ■ ^sin ( ф 13 ) ^{+ 1} 2 ■ ^sin ( ф 23 ⁺ ф 13 ^{- 180} ° ) .

Поворотная платформа представляет собой равносторонний треугольник с вершинами 3 , 6 , 9 . Зная координаты этих точек, можно найти уравнение плоскости поворотной платформы, а затем и координаты нормали N в базовой системе координат.

Уравнение плоскости поворотной платформы записывается следующим образом:

A · x + B · y + C · z + D = 0.

По координатам трех точек 3 , 6 , 9 получают коэффициенты уравнения плоскости верхней платформы:

A = y 30 ( z 60 – z 90 ) + y 60 ( z 90 – z 30 ) + y 90 ( z 30 – z 60 ),

B = z ₃₀( x ₆₀ – x ₉₀) + z ₆₀( x ₉₀ – x ₃₀) + z ₉₃( x ₃₃ – x ₆₀),

C = x ₃₀( y ₆₀ – y ₉₀) + x ₆₀( y ₉₀ – y ₃₀) + x ₉₀( y ₃₀ – y ₆₀),

–D = x30(y60 · z90 – y90 · z60) + x60(y90 · z30 – y30 · z90) + + x90(y30 · z60 – y60 · z30), где коэффициенты A, B, C – координаты вектора нормали N к плоскости поворотной платформы 3, 6, 9 (см. рис. 3). Направляющие косинусы вектора N относительно базовой системы координат X0Y0Z0 рассчитывают по формулам

cos a =	A
	A 2	+ B в	+ C 2
cos P =		B
	A 2	+ B B	+ C в
cos y =		C
	A 2	+ B B 2	+ C в

За обобщенные координаты поворотной платформы приняты два: угла α, β – и высота полюса схвата Z P . Третий из углов наклона плоскости поворотной платформы γ не следует включать в обобщенные координаты, поскольку положение плоскости в пространстве однозначно определено двумя углами и высотой. Кроме того, число степеней свободы дельтамеханизма, вычисленное по формуле Чебышева– Малышева, равно трем [5], а число обобщенных координат должно быть равно числу степеней свободы механизма. Координату Z P вычисляяют как среднее арифметическое координат Z трех точек, так как треугольник, образованный точками 3 , 6 , 9 , является равносторонним:

^ZP =

z 30 ⁺ z 60 ⁺ z 90

Результаты решения прямой задачи кинематики манипулятора параллельной структуры представлены в таблице.

Координаты поворотной платформы

Координаты схвата в базовой системе координат X 0 Y 0 Z 0	Координаты, определенные в САПР CATIA	Координаты, рассчитанные аналитически в пакете Maple	Отклонение, %
α	85,131°	85,011°	0,14
β	103,493°	103,514°	–0,02
γ	14,376°	14,437°	–0,42
Z P	85,587 мм	85,574 мм	0,02

Определение рабочей зоны манипулятора. Допустимые значения координат положения верхней платформы Z P , α, β определяются следующими параметрами механизма:

• –    длиной звеньев l 1 , l 2 ;

• –    максимальным и минимальным углами поворота сферических шарниров: по оси Х – θ max , θ min , по оси Y – ω max , ω min ;

• –    максимальным и минимальным углами поворота сферических шарниров φ 12max , φ 12min .

Определить максимальные углы наклона платформы в базовой системе координат α и β, высоту полюса схвата Z P , а также зависимость между ними можно с помощью трехмерной модели дельтамеханизма (рис. 4).

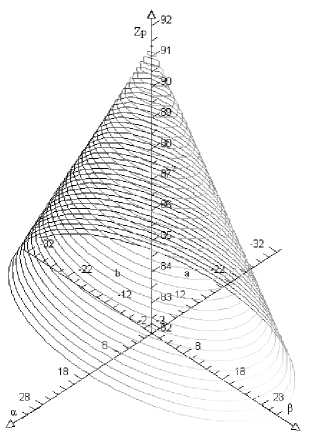
Рис. 4. Рабочая зона дельта-механизма

В ходе экспериментов с трехмерной моделью получена область рабочей зоны механизма – конус с эллиптическим основанием, описываемый уравнением

Z P =- 8,814

I a ²

16,5412

■         '■■

31,1182

+ 91,4.

Таким образом, при помощи трехмерного моделирования определена рабочая зона механизма – это конус с эллиптическим сечением. При максимальной высоте Z P поворот платформы невозможен. Снизу рабочая зона ограничена максимальными углами поворота шарниров 1 , 4 , 7 , а также длинами l 1 , l 2 .

Авторами представлены трехмерная модель манипулятора с параллельной структурой – дельтамеханизма – и аналитическое решение прямой задачи кинематики этого манипулятора. Проверка вычисленных координат поворотной платформы показала правильность полученного решения. С помощью трехмерной модели дельта-механизма также найдена рабочая зона манипулятора.

Полученные результаты могут быть использованы при проектировании аналогичных манипуляторов.